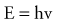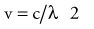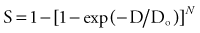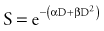CHAPTER 77 Radiotherapy for Head and Neck Cancer
Radiation Physics, Radiobiology, and Clinical Principles
Clinical Principles of Radiotherapy
Toward the closing years of the nineteenth century, many investigations into electricity characteristics were conducted, one of them demonstrating that electric potential placed across two separated platinum electrodes produces a spark.1 British physicist William Crookes demonstrated that if the two electrodes were placed within an evacuated glass tube, the vacuum would eventually cause the walls of the vessel to fluoresce.2 On November 8, 1895, Wilhelm Roentgen, while performing an experiment with the Crookes tube, accidentally left a piece of paper painted with barium platinocyanide nearby; he noted that the paper fluoresced and realized that this fluorescence of the paper could have been caused by a new, invisible type of ray that the tube was now emitting. Thus, the x-ray was discovered.
Radioactivity was discovered shortly after by Henri Becquerel, who investigated the capability of different substances to produce x-rays. He observed the darkening of photographic plates by uranium salts and concluded that the same x-rays were emitted spontaneously and continuously from the uranium.3 Pierre and Marie Curie, who read his results, coined the term radioactivity to describe this phenomenon. In 1898 they isolated a material with radioactivity 60 times higher than uranium and called it radium.4
These discoveries led to radiation biology experiments. The first documented experiment was performed unintentionally at about the same time, when Antoine Becquerel developed a “burn” on his chest from carrying a vial of radium salt in his vest pocket. It soon became apparent that radiation had the ability to produce profound biologic changes. In the beginning it was believed to be a magical cure for almost every known illness. The first documented success was reported in 1899 in Stockholm5 by Thor Stenbeck, who treated a 49-year-old woman’s nasal basal-cell carcinoma. He delivered 100 treatments in the course of 9 months, and the patient was alive and well 30 years after the treatment. In 1901, Dr. Frand Williams in Boston reported on the successful treatment of a lip cancer.5 The early treatments often involved very large single exposures that resulted in extensive skin toxicities and other complications. Therefore, only superficial sites were originally treated by the direct application of radium.6 Eventually, physicians started to insert radium directly into deep-seated tumors, effectively beginning the field of brachytherapy.7
The use of external beam treatments made its leap in 1922 when Coutard and Hautant reported a new concept of fractionated treatments: advanced laryngeal cancer could be cured without severe toxicities using fractionated treatments.8 Advances in measurements were also achieved when the skin erythema dose (the dose of x-rays required to give a light skin reaction) was replaced by the roentgen in 1928,9 which was later replaced by the rad. The rad is the unit of absorbed dose and is a measure of the energy deposition per unit mass by all types of ionizing radiation. The next step was achieved with the development of higher-energy machines capable of depositing dose at depth.
Basic Physics
Characteristics of Radiation
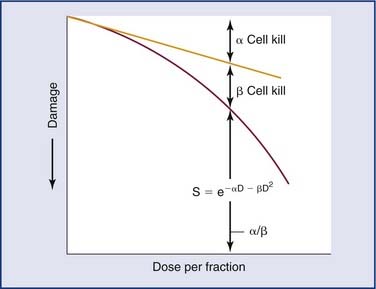
Radiation refers to the propagation of energy through space or a medium (Fig. 77-1). Radiation can be broadly classified as either particulate or electromagnetic. If the radiant energy is carried off by a particle that has rest mass, the radiation is called “corpuscular” or “particulate” radiation. Examples of particulate radiations are electrons, beta particles, protons, neutrons, and heavy charged particles.
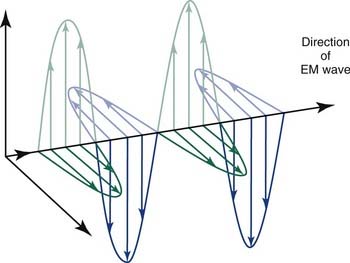
Figure 77-1. Propagation of electromagnetic (EM) radiation with oscillating electric and magnetic fields.
(From Saw CB. Foundation of Radiological Physics. Omaha, NE: C. B. Saw Publishing; 2004:10, with permission.)
where h is Planck’s constant, having a value of 6.626 × 10−34 joule-second (J.s). The energy of a photon is often expressed in electron volts (eV). One eV represents the amount of energy required to accelerate an electron through a potential of one volt. The frequency (ν) of a photon is related to its wavelength (λ) as follows:
where c = 3.0 × 108 m/sec, the speed of light in a vacuum. The waves of electromagnetic radiation are composed of oscillating electric and magnetic fields that are orthogonal to each other and to the direction of propagation, as shown in Figure 77-1. The electromagnetic spectrum spans a broad and continuous range from radiowaves to x-rays with wavelengths from 106 to 10−13 m. Radiation with wavelengths shorter than visible light is classified as ultraviolet rays, x-rays, and gamma rays. The boundaries between these regions are not sharply defined. For example, x-rays and gamma rays are indistinguishable except for their origins, one from the orbital electrons and the other from the nucleus, respectively. Different types of electromagnetic radiation interact differently with the same material (see Fig. 77-1).
Radiation Production from Linear Accelerators
Another type of radiation is termed bremsstrahlung11 (German for “braking radiation”), electromagnetic radiation produced by a sudden slowing down or deflection of charged particles (especially electrons) passing through matter near the strong electric fields of atomic nuclei.
Interaction of X-Rays with Matter
The most important of these interactions in RT are represented in Figure 77-2.
Figure 77-2. The major radiation interactions. e, electron; n, neutron; p, proton.
(Redrawn from Cox JD, Ang KK, eds. Radiation Oncology: Rationale, Technique, Results. 8th ed. St. Louis: Mosby; 2003:5.)
Radiation in Conventional Medicine
Linear accelerators (linacs) produce megavoltage x-rays. Commercially available medical linear accelerators produce x-rays and electrons with an energy range from 4 MeV up to around 25 MeV.11 The x-rays themselves are produced by the rapid deceleration of electrons in a target material, typically a tungsten alloy, which produces an x-ray spectrum via bremsstrahlung radiation. The shape and intensity of the beam produced by a linear accelerator may be modified or collimated by a variety of means. Thus, conventional, conformal, intensity-modulated, tomographic, and stereotactic radiotherapy are all produced by specially modified linear accelerators (Fig. 77-3).
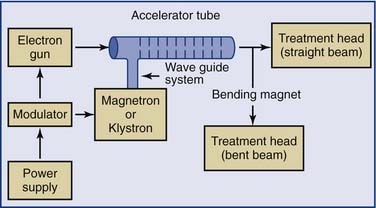
Figure 77-3. Block diagram of a typical medical linear accelerator.
(From Leibel SA, Phillips TL, eds. Textbook of Radiation Oncology. Philadelphia: WB Saunders; 1998:110.)
Additional magnetic or electrostatic lens elements may be included to ensure that the beam remains in the center of the tube and its electrodes (see Fig. 77-3).
Linear Accelerators
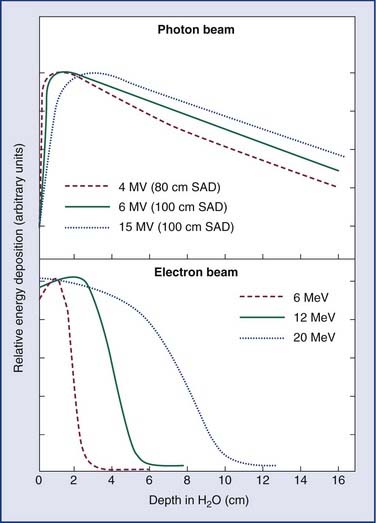
As an energy source, electrons differ from photons in that electrons travel only a certain (short) distance within tissue. They are very light particles compared with the nuclei of the target tissue with which they interact. Hence, the electrons lose a large fraction of their energy in a single process. This leads to much less skin sparing and the deposition of the majority of the dose in superficial tissues. Consequently, however, they are very useful for treatments in which the target of the radiation lies close to the surface of the patient, such as skin tumors (Fig. 77-4).
Particle Beams
One particle for which there has been a great amount of clinical work is the fast neutron.12,13 Fast neutrons are of clinical interest because of their radiobiologic properties, which occur because of the much greater amount of energy they deposit when they go through tissue. Neutrons are neutral particles and interact with the atomic nuclei, producing “heavy” charged particles such as protons, α-particles, or nuclear fragments that in turn create a dense chain of ionization events as they go through tissue. The distribution of these secondary particles depends on the energy spectrum of the neutron beam, so the biologic properties of the beam depend strongly on its energy spectrum. Neutrons used in therapy generally are produced by accelerating charged particles, such as protons or deuterons, and impacting them on a beryllium target.
There is considerable interest in using charged particle beams directly for therapeutic purposes, which generally requires beams of much higher energy than those used to produce neutrons. The lighter particles, such as protons14 and α-particles, are of interest because of their extremely favorable depth-dose characteristics. The radiobiologic properties of these beams are similar to those of conventional photon or electron beams. Heavy charged particles combine the favorable depth-dose properties of the proton and α-particle beams with the favorable biologic properties of the neutron beams. Energies are on the order of several hundred MeV per nucleon, rather than the few MeV per nucleon for the recoil fragments produced by neutrons. These highly energetic particles do not deposit much energy in tissue until they reach the end of their path, where they are moving slowly. Hence, they do not produce much radiation damage in the intervening tissues. Because of their extremely high cost and general unavailability, however, these beams are not widely in use. Interest in proton beams has grown, and the number of radiotherapy facilities using protons in the United States is expected to rise.
Treatment Aspects of External Beam Radiation
Typically, the radiation dose is delivered to the patient using a linear accelerator (Fig. 77-5). The radiation beam as produced is a forward peak; that is, it has extremely high intensity along the beam axis. It must pass through a conical metallic flattening filter to create a uniform field beam for clinical use. As the clinical beam exits the linear accelerator, it is collimated by a pair of jaws or a multileaf collimation (MLC) system (see Fig. 77-5). The multileaf collimation system is used to shield and protect normal structures (replacing the antiquated and cumbersome lead blocks). In addition, the system is used to modulate beam intensity in intensity-modulated RT. The linear accelerator has a gantry that allows the rotation of the treatment head around the patient. Hence, the radiation beam can be directed at the target from multiple positions to reduce dose to the normal tissues. Because of the high voltage, moving parts, and high dose, the linear accelerator must be properly calibrated and properly maintained for its safe use (see Fig. 77-5).
Radiobiology
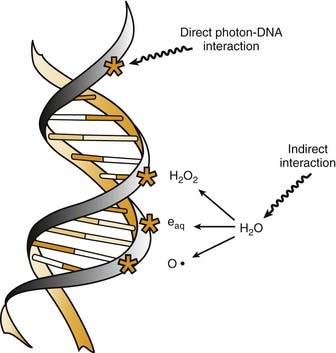
Radiation cell killing occurs when critical targets within the cell are damaged by radiation.15 A number of biologic molecules or structures are potential targets for radiation damage. According to most studies DNA is the most critical target for the biologic effects of radiation. On a molecular level, this effect requires the production of ionizations, which is why we refer to the process as ionizing radiation. The damage can occur directly when the radiation is absorbed by the DNA itself, because the atoms of the DNA become ionized and damaged. More commonly, however, it occurs indirectly through the following three modes of action15,16:
All of these species are highly reactive free radicals that, in turn, interact with the DNA and cause damage. Both ways eventually cause broken bonds in the DNA backbone, which can cause double-strand breaks, ultimately resulting in mitotic death (Fig. 77-6).
These broken bonds can result in the loss of a base or of the entire nucleotide, or in complete breaking of one or both of the strands of DNA. Single-strand breaks are easily repaired with use of the opposite strand as a template. Therefore, single-strand breaks show little relation to cell killing, although they might result in mutation if the repair is incorrect. Double-strand breaks, on the other hand, are thought to be the most important lesion in DNA produced by radiation.18 Double-strand breaks, as the name implies, results in snapping of the chromatin into two pieces. These double-strand breaks can result in mutations or, most important, in cell killing.
A growing body of experimental data suggests that radiation damage to DNA is not the only mechanism by which ionizing radiation damages cells. Other mechanisms are apoptosis, cell cycle arrest, and mitotic death. One study has suggested that apoptosis can be triggered by radiation energy deposition in cell membranes.19 It has also been reported that direct radiation damage to mitochondria can trigger apoptosis.20
Cell Cycle Arrest
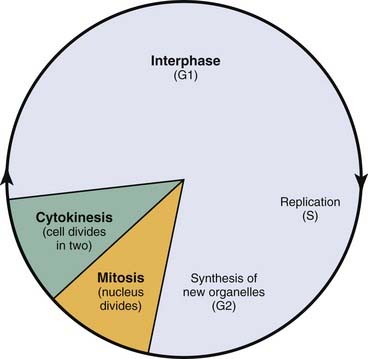
Radiation triggers signaling cascades leading to arrest, usually at the G1 and G2 checkpoints in the cell cycle.21 Cell cycle perturbations (Fig. 77-7) are seen characteristically after radiation exposure and were among the earliest observed biologic effects of radiation. Cells can show checkpoints or arrest in any phase of the cell cycle, although the best-described checkpoints with respect to radiation damage are the G1 and G2 checkpoints. Normal cells and those cancer cells that retain p53 function are blocked in the G1 phase of the cell cycle. This is a p53-mediated event.
Radiosensitivity
Our main interest in radiobiology is in figuring out ways to improve the treatment toxicity ratio. One of the main concepts is radiation sensitivity, which refers to the relative susceptibility of cells, tissues, tumors, or organisms to radiation. However, tumor regression is not solely a function of tumor cell death, but is influenced by many factors, including the amount of extracellular stroma, the propensity of the tumor cells to undergo rapid rather than delayed death, and the resorption of radiation-inactivated cells (depopulation). A frequent misconception is that tumors should be more radiosensitive than normal tissues because they proliferate more rapidly. This misconception may go back 100 years. In 1906, only 11 years after the discovery of x-rays, Bergonie and Tribondeau formulated a “law” for the relationship between cellular radiosensitivity and reproductive capacity.22 They postulated that cells that have a higher proliferation rate are more radiosensitive than slowly proliferating cells. On a purely cellular basis, it is correct that cells in mitosis at the time of irradiation are more radiosensitive than cells in other phases of the cell cycle. However, many other factors, such as tissue- and host-specific factors, have important influence. In 1906, there was no appreciation of late-occurring normal tissue complications. Nowadays, we know that many slowly proliferating or nonproliferating normal tissues, such as the kidney, are highly radiosensitive; they just express radiation injury much later than rapidly proliferating tissues. Similarly, the proliferation rate of tumors does not predict their radio-curability. For example, rapidly proliferating tumors such as glioblastoma multiforme can be highly radioresistant.
Cell Survival
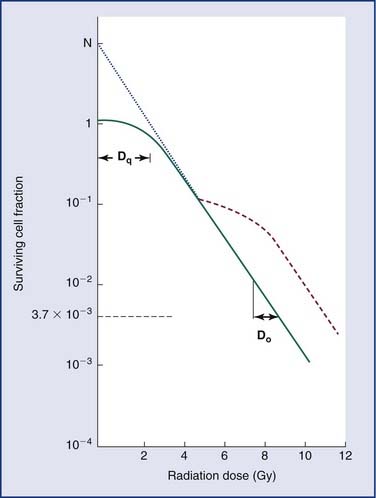
Loss of reproductive integrity in long-term survival assays is important to our understanding of the response of either a tumor or a normal tissue to radiation. When cells are exposed to lethal doses of radiation, they may not die immediately or within a few hours of treatment, or even sometimes within a single division of radiation. When cells have been observed by time-lapse cinematography after irradiation, some cells survive and go on to form colonies, and some die quickly. Others go through up to several rounds of abortive cell division before finally ceasing to divide. Radiation biologists have demonstrated that it is the proportion of cells capable of forming a colony by sustained cell division that most fully predicts the effects of a dose of radiation.23 In order to eradicate or control a tumor; one must inactivate all clonogenic tumor cells. In other words, the treatment may fail if only one clonogen survives, because that cell can give rise to a regrowing tumor. In order to understand tumor control better, plots of the surviving fraction of cells as a function of the radiation dose have been performed. An example is shown in Figure 77-8.
By convention, the surviving cell fraction is plotted on a logarithmic scale, and the radiation dose is plotted on a linear scale. This curve is representative of most mammalian cells. Consider the solid curve in Figure 77-8, which represents the survival data. Note that there are two distinct regions to the curve. There is an initial region for low radiation doses, where the slope of the curve is shallow. In this region, small incremental changes in the amount of radiation are not very effective at increasing the number of cells killed. This is called the shoulder region, and its width is characterized by the parameter Dq. It is the distance along the dose axis at a surviving fraction of unity between the abscissa and the point where the extrapolated linear portion of the curve is intersected. It is a measure of the ability of the cells to repair small amounts of radiation damage. At higher doses of radiation, the curve becomes a straight line on a semilog plot. Its slope is characterized by Do, which is the incremental dose change required to reduce the surviving cell fraction to 1/e of its value. The steeper the slope in this region, the smaller is the value of Do and the more radiosensitive is the cell line. When extrapolated back to a zero radiation dose, it intersects the abscissa at a value N. A curve of this type can be modeled using the following equation:
where S is the surviving fraction, D is the radiation dose, and N and Do are as indicated in Figure 77-8. In target theory, N can be thought of as the number of distinct targets in the cell that should receive one radiation “hit” before the cell is inactivated.
A number of mathematical models have been devised to attempt to describe the shape of the cell survival curves that are observed experimentally, with an initial shallower slope, an eventual bending (the “shoulder”), and a final, steeper slope. These include target models, lethal and potentially lethal damage models, and repair saturation models. Some of these have been based on simple mathematical modeling without any real attempt to model known molecular events involved in cell killing, whereas others have been based on attempts to model some of the known molecular events (e.g., chromosome breaks or DNA repair) that are involved in cell killing. All of the models can describe the shape of the survival curve to a first approximation. None does so perfectly, and none takes into account all the events and all of the possible mechanisms involved in cell death. A model that has been most influential on clinical practice is the linear quadratic model,24 because it is one of the models that best fits the behavior of cells after exposure to radiation doses within the range used in the clinic. The linear-quadratic model was devised by Keller and Rossi,25 who proposed that radiation-induced cell killing resulted from two potential events, one with a linear relation to dose (exp[−αD]), the other having a quadratic relation to dose (exp[−βD2]). This was expressed mathematically by the “alpha-beta” equation, as follows:
where S represents survival of a cell population after a dose, D (Fig. 77-9). It has been hypothesized that this equation actually represents a molecular reality.26 Double-strand breaks in the DNA are lethal lesions that are produced by either one energy deposition, an event termed (αD), or by two separate events, each involving a single strand of DNA (βD2), which then interact. This hypothesis is now thought to be unlikely because of the low probability of two tracks interacting within a single double helix.
The α/β ratio, which is derived from Equation 77-4, represents a point on the survival curve at which the components of cell killing are equal to each other—that is, αD = βD2, or D = α/β. In other words, for each cell population there is a dose of radiation in which the linear (α) and quadratic (β) contributions to cell killing are equal. The α/β ratio is specific to each cellular population and reflects the sensitivity of the cell to the two types of damage. Tissues that have an early response to radiation (skin, mucosa, and tumor cells) have a high α/β ratio. In other words, their survival curves stay straight for a longer period before the bend occurs, in which there is a higher contribution of single-event or α killing. Late-responding tissues, such as spinal cord, kidney, and muscle, have survival curves that bend earlier, with resultant lower α/β ratios. These late-responding tissues have shoulders on their survival curves within the range of doses commonly used in RT. This understanding led to the concept that altered fractionation schedules could be used to treat tumor populations more effectively with respect to damage to late-responding tissues.
Tissue-Radiation Characterizations
The main intent in clinical radiotherapy is to irradiate tumoral tissues while minimizing the damage to the surrounding healthy tissues. The four main concepts of clinical radiotherapy are known as “the four Rs of radiotherapy”: repair (of sublethal damage), redistribution (across the cell cycle), repopulation, and reoxygenation. Radiotherapy basically works not because tumors are more radiosensitive than normal tissue but because normal tissues are better at repair and repopulation. These four Rs also account for different response rates of tumors.27–29
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree