Figure 4-1 Contact lens. Note the relationship among the parts. (Modified with permission from Stein HA, Freeman MI, Stein RM. CLAO Residents Contact Lens Curriculum Manual. New Orleans: Contact Lens Association of Ophthalmologists; 1996. Redrawn by Christine Gralapp.)
Contact Lens Glossary
It is important for ophthalmologists to know the vocabulary related to contact lenses. The 3 most important terms are base curve, diameter, and power (Fig 4-1):
Base curve The curvature of the central posterior surface of the lens, which is adjacent to the cornea; it is measured by its radius of curvature (mm) or may be converted to diopters (D) by taking the reciprocal of the radius.
Diameter (chord diameter) The width of the contact lens, which typically varies with the lens material; the diameter of soft contact lenses, for example, ranges from 13 mm to 15 mm, whereas that of rigid gas-permeable (RGP) lenses ranges from 9 mm to 10 mm.
Power Determined by lens shape and calculated indirectly by Snell’s law: D = [n2 – n1]/r; for measurement of the posterior vertex power (as with spectacles), the lens (convex surface facing the observer) can be placed on a lensmeter.
The following terms are also important to know:
Apical zone The steep part of the cornea, generally including its geometric center; usually 3–4 mm in diameter.
Corneal apex The steepest part of the cornea.
Dk The oxygen permeability of a lens material, where D is the diffusion coefficient for oxygen movement in the material and k is the solubility constant of oxygen in the material.
Dk/L A term describing the oxygen transmissibility of the lens; depends on the lens material and the central thickness (L).
Edge lift Description of the peripheral lens and its position in relation to the underlying cornea; adequate edge lift (as documented during fluorescein evaluation by a ring of fluorescein appearing under the lens periphery) prevents edges from digging into the flatter corneal periphery.
Fluorescein pattern The color intensity of fluorescein dye in the tear lens beneath a rigid contact lens. Areas of contact appear black; green reflects clearance between the lens and the cornea.
K reading Keratometry reading; determined by a manual or automated keratometer.
Lenticular contact lens A lens with a central optical zone and a nonoptical peripheral zone known as the carrier; designed to improve lens comfort.
Optic zone The area of the front surface of the contact lens that has the refractive power of the lens.
Peripheral curves Secondary curves just outside the base curve at the edge of a contact lens. They are typically flatter than the base curve to approximate the normal flattening of the peripheral cornea. Typically, junctions between posterior curves (base curve and peripheral curve, for example) are smoothed or “blended” to enhance lens comfort.
Polymethylmethacrylate (PMMA) The first plastic used in the manufacture of contact lenses.
Radiuscope A device that measures radius of curvature, such as the base curve of an RGP lens. Flatter surfaces have larger radii of curvature, and steeper surfaces have smaller radii of curvature.
Sagittal depth or vault A term describing the depth (or vault) of a lens; measuring the distance between the center of the posterior surface (or the center of the base curve) to the plane connecting the edges of the lens determines sagittal depth. In general, if the diameter is held constant, the sagittal depth decreases as the base curve increases. Although sagittal depth is critical for determining good fit, designation of the base curve for a particular lens type typically ensures the appropriate sagittal depth.
Tear lens The optical lens formed by the tear-film layer between the posterior surface of a contact lens and the anterior surface of the cornea. In general, with soft lenses, the tear lens has plano power; with rigid lenses, the power varies, depending on the shape of the lens and the cornea.
Wetting angle The wettability of a lens surface. A low wetting angle means water will spread over the surface, increasing surface wettability, whereas a high wetting angle means that water will bead up, decreasing surface wettability. A lower wetting angle (greater wettability) generally translates into greater lens comfort and better lens optics.
Clinically Important Features of Contact Lens Optics
Contact lenses and conventional lenses have 4 parameters in common: posterior surface curvature (base curve), anterior surface curvature (power curve), diameter, and power (see Fig 4-1). However, unlike for spectacle lenses, the shape of contact lenses’ posterior surface is designed primarily to have certain fitting relationships with the anterior surface of the eye.
The refractive performance of contact lenses differs from that of spectacle lenses for 2 primary reasons: (1) contact lenses have a shorter vertex distance and (2) tears, rather than air, form the interface between the contact lens and the cornea. Unique optical considerations that are related to contact lenses include field of vision, image size, accommodation, convergence demand, the tear lens, correction of astigmatism, and correction of presbyopia. Each type of contact lens has unique optical considerations (Table 4-1).
Table 4-1

Field of Vision
Spectacle frames reduce the field of vision by approximately 20°. Owing to their proximity to the entrance pupils and lack of frames, contact lenses provide a larger field of corrected vision and avoid much of the peripheral distortion, such as spherical aberration, created by high-power spectacle lenses.
Image Size
Retinal image size is influenced by the vertex distance and power of corrective lenses. Contact lenses have shorter vertex distances than do spectacles, so image size changes less with contact lenses than with spectacles.
Anisometropia and image size
Axial ametropia is predominant in eyes with higher (non–surgically induced) refractive errors. Theoretically, the anisometropic aniseikonia of such eyes is minimized when the corrective lens is placed in the eyes’ anterior focal plane (see discussion of Knapp’s law in Chapter 1), which is, on average, approximately 15.7 mm anterior to the corneal vertex. In axial myopia, moving the corrective lens posterior to the eye’s focal plane (closer to the cornea) increases the size of the retinal image compared with that of an emmetropic eye. The reverse is true in axial hyperopia. In practice, however, using contact lenses to correct the refractive error of the eyes is usually best for managing anisometropia because anisophoria generated by induced prism in off-axis viewing of spectacle lenses is eliminated. In addition, the greater separation between the elements in the stretched retinas of larger myopic eyes may explain the less-than-perceived magnification observed with contact lenses. Surgically induced anisometropia (resulting from, for example, cataract or refractive surgery) without an axial component is usually managed best through use of contact lenses or additional surgery; in either method, the images will be closer in size than if spectacles are used.
Monocular aphakia and aniseikonia
Minimizing aniseikonia in monocular aphakia improves the functional level of binocular vision. An optical model of surgical aphakia can be represented by inserting a neutralizing (minus-power) lens in the location of the crystalline lens and correcting the resulting ametropia with a forward-placed plus-power lens. Doing so effectively creates a Galilean telescope within the optical system of the eye. Accordingly, magnification is reduced as the effective plus-power corrective lens (corrected for vertex distance) is moved closer to the neutralizing minus-power lens (the former site of the crystalline lens). This model illustrates why contact lens correction of aphakia creates significantly less magnification than does a spectacle lens correction; a posterior chamber intraocular lens creates the least magnification of all.
Although the ametropia of an aphakic eye is predominantly refractive, it can also have a significant preexisting axial component. For example, the coexistence of axial myopia would further increase the magnification of a contact lens–corrected aphakic eye (compared with the image size of the spectacle-corrected fellow phakic myopic eye). Even if the image size of the fellow myopic eye were to be increased by fitting this eye with a contact lens, the residual aniseikonia might still exceed the limits of fusion and cause diplopia (Clinical Example 4-1). Divergent strabismus can develop in aphakic adult eyes (and esotropia may develop in children) if fusion is interrupted for a significant period. If diplopia does not resolve within several weeks, excessive aniseikonia should be suspected and confirmed by demonstration of the patient’s inability to fuse images superimposed with the aid of prisms. Such patients are usually aware that the retinal image in the aphakic eye is larger than that in the fellow phakic eye.
Clinical Example 4-1
Fitting a unilateral aphakic eye causes diplopia that persists in the presence of prisms that superimpose the 2 images. The refractive error of the fellow eye is –5.00 D, and the image of the aphakic eye is described as being larger than that of the fellow myopic eye. How can the diplopia be resolved?
The goal is to reduce the aniseikonia of the 2 eyes by magnifying the image size of the phakic eye and/or reducing the image size of the contact lens–corrected aphakic eye. To achieve the former, correct the myopic phakic eye with a contact lens to increase its image size. If doing so is inadequate, overcorrect the contact lens by 5.00 D and prescribe a spectacle lens of –5.00 D for that eye, thereby introducing a reverse Galilean telescope into the optical system of the eye. (If, however, the phakic eye were hyperopic, its image size would be increased by correcting its refractive error with a spectacle lens rather than a contact lens.)
When the fellow phakic eye is significantly myopic, correcting it with a contact lens increases its image size and often reduces the aniseikonia sufficiently to resolve the diplopia. If excessive aniseikonia persists, the clinician should aim to further reduce the image size of the contact lens–corrected aphakic eye. Overcorrecting the aphakic contact lens and neutralizing the resulting induced myopia with a forward-placed spectacle lens of appropriate minus power can achieve the additional reduction in image size. In effect, this process introduces a reverse Galilean telescope into the optical system of that eye. Empirically, increasing the power of the distance aphakic contact lens by +3 D and prescribing a –3 D spectacle lens for that eye usually suffice. Alternatively, if it is impractical to fit the fellow myopic eye with a contact lens, the clinician may elect to add plus power to the aphakic contact lens by an amount equal to the spherical equivalent of the refractive error of the fellow eye, in effect equalizing the myopia of the 2 eyes. The resulting decrease in the residual aniseikonia usually improves fusional potential and facilitates the recovery of fusion even of significant aniseikonic exotropia over several weeks. However, the resolution of aphakic esotropia or cyclotropia is less certain.
In contrast with axial myopia, coexisting axial hyperopia reduces the magnification of a contact lens–corrected aphakic eye. Residual aniseikonia can be further mitigated by correction of the fellow hyperopic eye with a spectacle lens (rather than a contact lens) to maximize image size.
Infantile aphakia
Management of aphakia in infants and young children represents a challenge because of the possibility of amblyopia and permanent vision loss. Contact lens wear may be ineffective in children because of poor patient adherence; therefore, intraocular lens implants may be a better option. Aphakia may be corrected in infants with contact lenses or lens implants. The optimal method in this group of patients is not yet known. The rapid change in axial length and corneal power during infancy (see Chapter 2) may make the selection of implant power difficult. Aggressive management of both optical correction and amblyopia treatment is necessary to achieve an optimal outcome in such young patients.
Autrata R, Rehurek J, Vodicková K. Visual results after primary intraocular lens implantation or contact lens correction for aphakia in the first year of age. Ophthalmologica. 2005;219(2):72–79.
Infant Aphakia Treatment Group; Lambert SR, Buckley EG, et al. The infant aphakia treatment study: design and clinical measures at enrollment. Arch Ophthalmol. 2010;128(1):21–27.
Accommodation
Accommodation is defined as the difference in vergence at the first principal point of the eye (1.35 mm behind the cornea) between rays originating at infinity and those originating at a near point. This disparity creates different accommodative demands for spectacle and contact lenses. Compared with spectacles, contact lenses increase the accommodative requirements of myopic eyes and decrease those of hyperopic eyes in proportion to the size of the refractive error. The difference between the accommodative efficiency of spectacle lenses and that of contact lenses results from the effect of these 2 modalities on the vergence of light rays as they pass through the respective lenses. Contact lens correction requires an accommodative effort equal to that of emmetropic eyes. In other words, contact lenses eliminate the accommodative advantage enjoyed by those with spectacle-corrected myopia and the disadvantage experienced by those with spectacle-corrected hyperopia. The accommodative advantage observed in patients with spectacle-corrected myopia is consistent with the clinical observation that patients with spectacle-corrected high myopia can read through their distance correction at older ages than can patients with emmetropia. The opposite is true of patients with spectacle-corrected hyperopia (Clinical Example 4-2).
Clinical Example 4-2
What is the accommodative demand of a –7 D myopic eye corrected with a spectacle lens compared with a contact lens? A 7 D hyperopic eye? Assume a vertex distance of 15 mm and a near-object distance of 33.3 cm.
The myopic refractive error of the first eye is –7 D at a vertex distance of 15 mm, and the object distance is 33.3 cm. The vergence of rays originating at infinity and exiting the spectacle lens is –7 D. Due to the vertex distance, the vergence of these rays at the front surface of the cornea (which is approximately the location of the first principal point) is –6.3 D. Use the focal point of the –7 D spectacle lens, 1/7 = 0.143 m, plus the vertex distance of 0.015 m (0.158 m) to find the vergence at the corneal surface: 1/0.158 m = –6.3 D (Fig 4-2A).
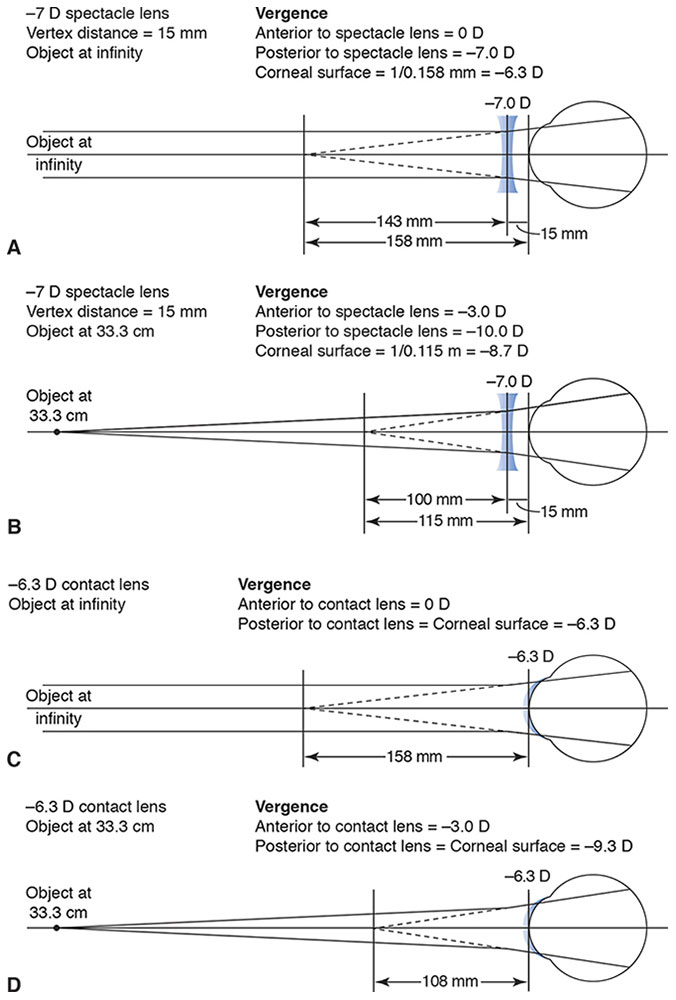
Figure 4-2 Accommodative demand. A, Effective spectacle lens power at the corneal surface. B, Accommodative demand with a –7.0 D spectacle lens. C, Correction with a –6.3 D contact lens. D, Accommodative demand with a –6.3 D contact lens. (Illustrations developed by Thomas F. Mauger, MD.)
The vergence of rays originating at a distance of 33.3 cm after exiting the spectacle lens is –10 D (Fig 4-2B). The vergence is calculated by using the vergence of the light after it leaves the spectacle lens: –3 + (–7) = –10. Due to the vertex distance, the vergence of these rays at the front surface of the cornea (which is approximately the location of the first principal point) is –8.7 D. Use the focal point of the vergence after the light travels through the lens, –10 D, 1/10 = 0.1 m, plus the vertex distance of 0.015 m (0.115 m) to find the vergence at the corneal surface: 1/0.115 m = –8.7 D).
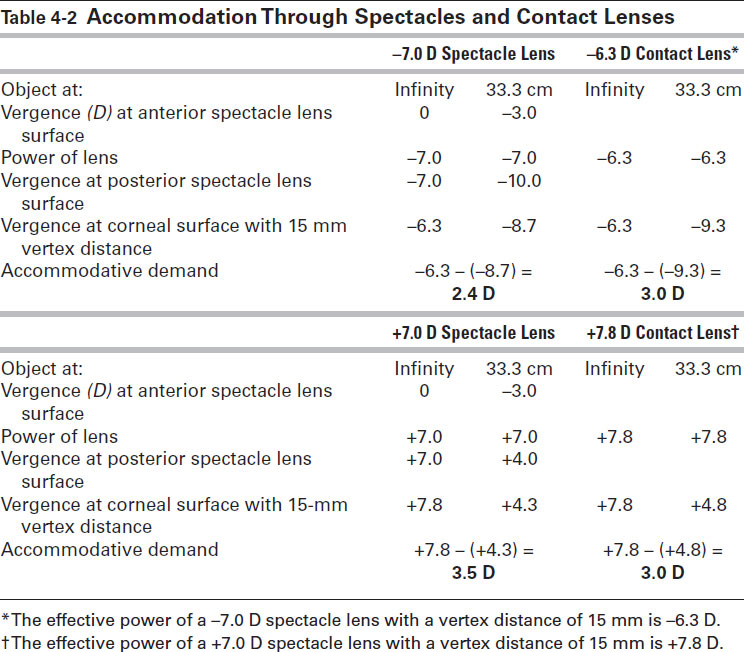
Accommodation is the difference between the vergence at the first principal point between rays originating at infinity and the vergence of rays originating at a distance of 33.3 cm. In this case, the accommodation is 2.4 D: –6.3 – (–8.7) = 2.4. In contrast, the accommodation required with a contact lens correction is approximately 3 D (Fig 4-2C, D). Therefore, this myopic eye would need 0.6 D more accommodation to focus an object at 33.3 cm when wearing a contact lens compared with correction with a spectacle lens. Similarly, the accommodative demands of an eye corrected with a +7 D spectacle lens would be 3.5 D compared with approximately 3 D for a contact lens (Table 4-2).
Table 4-2
Convergence Demands
Depending on their power, spectacle lenses (optically centered for distance) and contact lenses require different convergences. Myopic spectacle lenses induce base-in prisms for near objects. This benefit is eliminated with contact lenses. Conversely, hyperopic spectacles increase the convergence demands by inducing base-out prisms. In this case, contact lenses provide a benefit by eliminating the incremental convergence requirement.
In summary, correction of myopia with contact lenses, as opposed to spectacle lenses, increases both accommodative and convergence demands of focusing near objects proportional to the size of the refractive error. The reverse is true in hyperopia (Fig 4-3).
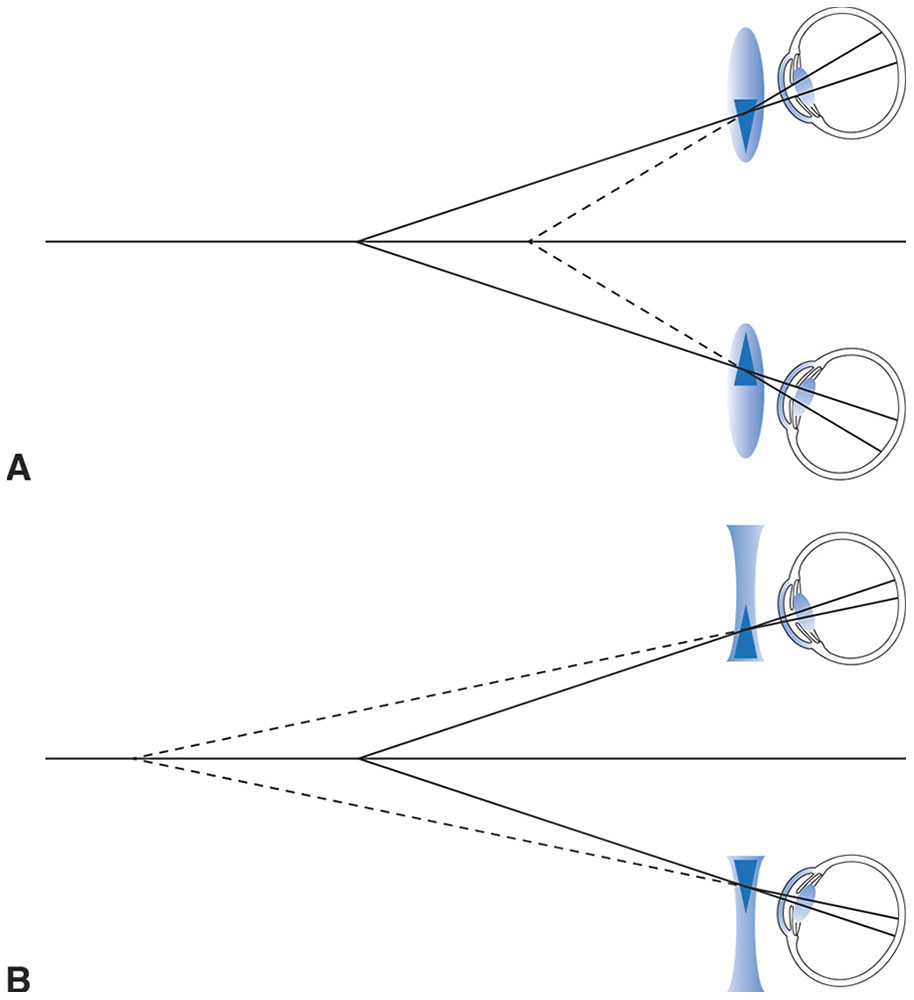
Figure 4-3 Effect of spectacle lenses on convergence demands. A, Lenses for correction of hyperopia create induced base-out prism with convergence, which increases the convergence demand. B, Lenses for correction of myopia create induced base-in prism, which decreases the convergence demand. (Illustrations developed by Thomas F. Mauger, MD.)
Tear Lens
The presence of fluid, rather than air, between a contact lens and the corneal surface is responsible for another major difference between the optical performance of contact lenses and that of spectacle lenses. The tear layer between a contact lens and the corneal surface is an optical lens in its own right. As with all lenses, the power of this tear, or fluid, lens is determined by the curvatures of the anterior surface (formed by the back surface of the contact lens) and the posterior surface (formed by the front surface of the cornea). Because flexible (soft) contact lenses conform to the shape of the cornea and the curvatures of the anterior and posterior surfaces of the intervening tear layer are identical, the power of their tear lenses is always plano. This statement is not generally true of rigid contact lenses: the shape of the posterior surface (which defines the anterior surface of the tear lens) can differ from the shape of the underlying cornea (which forms the posterior surface of the tear lens). Under these circumstances, the tear layer introduces power that is added to the eye’s optical system.
The power of the tear lens is approximately 0.25 D for every 0.05-mm radius-of-curvature difference between the base curve of the contact lens and the central curvature of the cornea (K), and this power becomes somewhat greater for corneas steeper than 7.00 mm. Tear lenses created by rigid contact lenses with base curves that are steeper than K (ie, have a smaller radius of curvature) have plus power, whereas tear lenses formed by base curves that are flatter than K (ie, have a larger radius of curvature) have minus power (Fig 4-4). Therefore, the power of a rigid contact lens must account for both the eye’s refractive error and the power introduced by the tear lens. An easy way of remembering this is to use the rules steeper add minus (SAM) and flatter add plus (FAP) (Clinical Example 4-3).
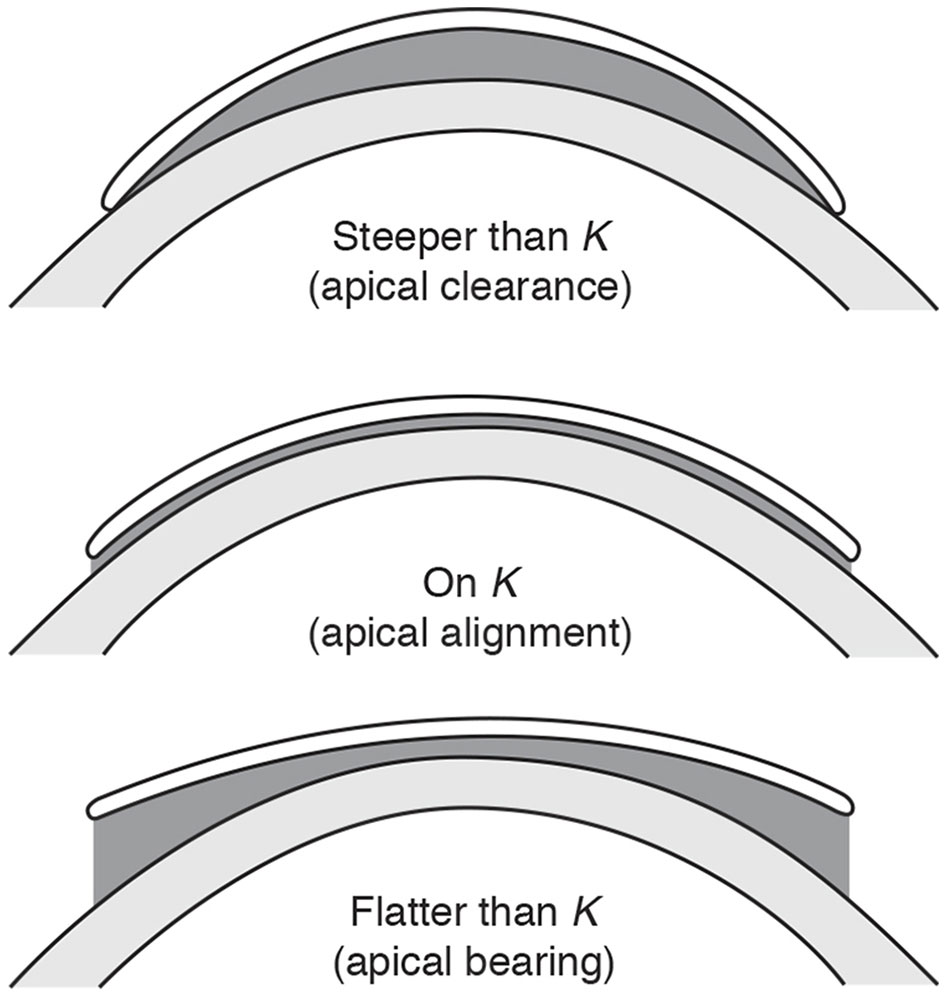
Figure 4-4 A rigid contact lens creates a tear (or fluid) lens whose power is determined by the difference between the curvature of the cornea (K) and that of the base curve of the contact lens. (Courtesy of Perry Rosenthal, MD. Redrawn by Christine Gralapp.)
Clinical Example 4-3
The refractive error of an eye is –3.00 D, the K measurement is 7.80 mm (43.25 D), and the base curve chosen for the rigid contact lens is 7.95 mm (42.50 D). What is the anticipated power of the contact lens?
The power of the resulting tear lens is –0.75 D. This power would correct –0.75 D of the refractive error. Therefore, the remaining refractive error that the contact lens is required to correct is –2.25 D (recall the FAP rule: flatter add plus). Conversely, if the refractive error were +3.00 D (hyperopia), then the necessary contact lens power would be +3.75 D to correct the refractive error and the –0.75 D tear lens (Fig 4-5).
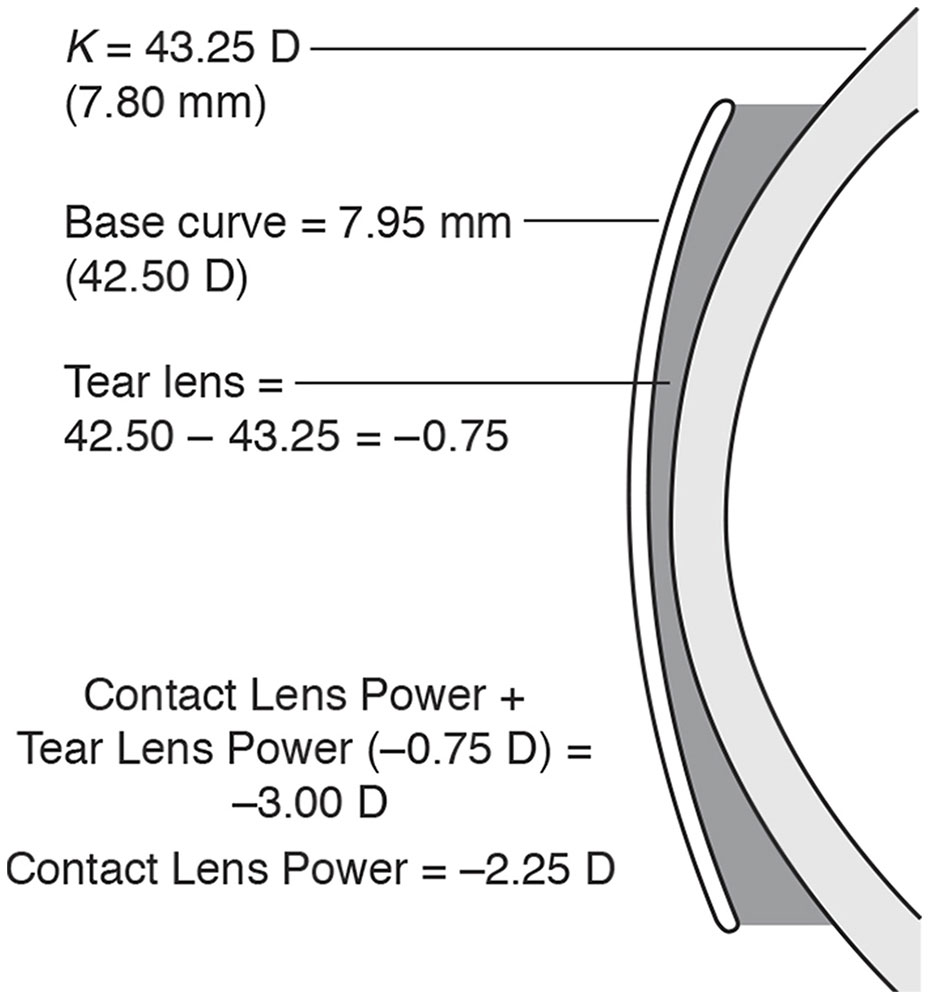
Figure 4-5 Determining the power of a contact lens using the FAP-SAM rules. (Illustration developed by Thomas F. Mauger, MD.)
Because the refractive index of the tear lens (1.336) is almost identical to that of a cornea (1.3765), the anterior surface of the tear lens virtually masks the optical effect of the corneal surface. If the back surface of a contact lens is spherical, then the anterior surface of the tear lens is also spherical, regardless of the corneal topography. In other words, the tear layer created by a spherical rigid contact lens neutralizes more than 90% of regular and irregular corneal astigmatism. This principle simplifies the calculation of the tear lens power on astigmatic corneas: because the powers of the steeper corneal meridians are effectively neutralized, they can be ignored, and only the flattest meridians need to be considered. The refractive error along the flattest meridian is represented by the spherical component of refractive errors expressed in minus cylinder form. For this reason, clinicians should use only the minus cylinder format when dealing with contact lenses (Clinical Example 4-4).
Clinical Example 4-4
The refractive correction is –3.50 +1.75 × 90, and the K measurements along the 2 principal meridians are 7.80 mm horizontal (43.25 D at 180°) and 7.50 mm vertical (45.00 D at 90°). The contact lens base curve is 7.50 mm. What is the anticipated power of the contact lens?
The refractive correction along the flattest corneal meridian (7.80 mm) is –1.75 D (convert the refractive error to minus cylinder form), and the lens has been fitted steeper than flat K, creating a tear lens of +1.75 D. Thus, a corresponding amount of minus power must be added (recall the SAM rule: steeper add minus), giving a corrective power of –3.50 D in that meridian.
The refractive correction along the steepest meridian (7.50 mm) is –3.50 D. The lens is fitted “on K”; therefore, no tear lens power is created. The corrective power for this meridian is also –3.50 D.
Accordingly, the power of the contact lens should be –3.50 D (Fig 4-6).
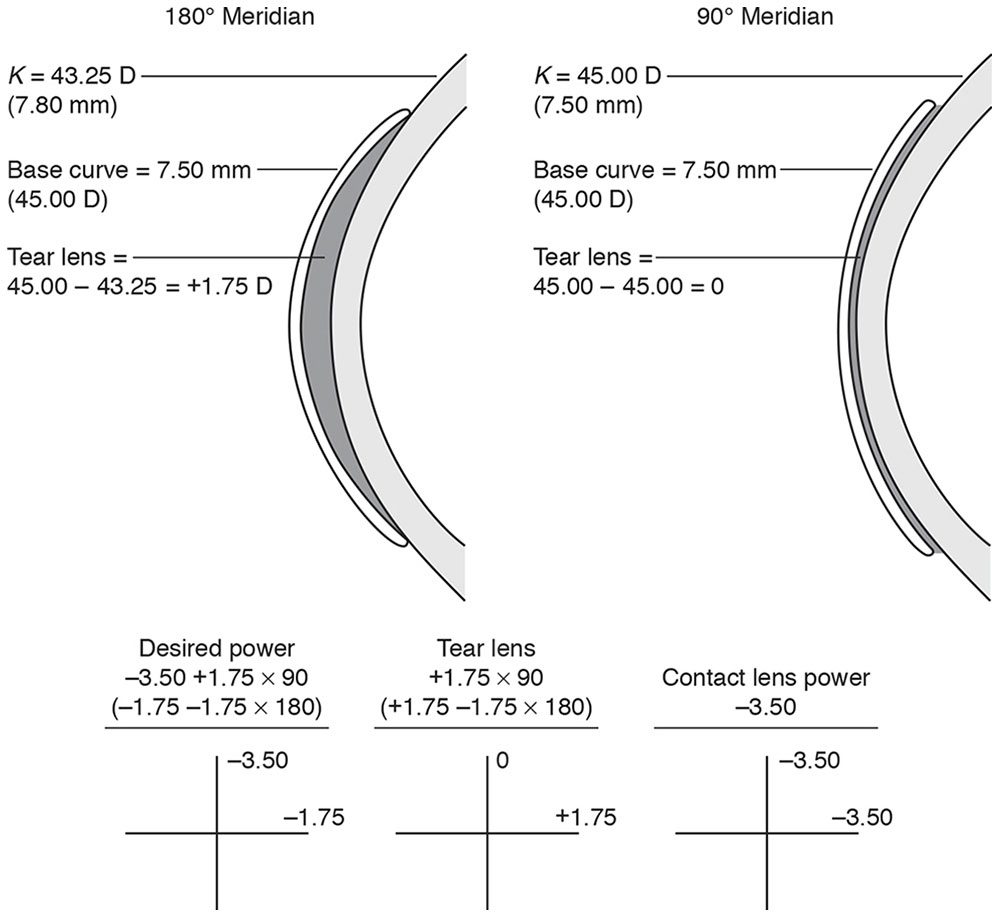
Figure 4-6 Determining the power of a contact lens using the FAP-SAM rules. (Illustrations developed by Thomas F. Mauger, MD.)
Correcting Astigmatism
Because rigid (and toric soft) contact lenses neutralize astigmatism at the corneal surface, the meridional aniseikonia created by the 2 different powers incorporated within each spectacle lens is avoided. For this reason, contact lens–wearing patients with significant corneal astigmatism often experience an annoying change in spatial orientation when they switch to spectacles. However, refractive astigmatism is the sum of corneal and lenticular astigmatism. Lenticular astigmatism, if present, is not corrected by spherical contact lenses. Because lenticular astigmatism usually has an against-the-rule orientation (vertical axis minus cylinder), it persists as residual astigmatism when the corneal astigmatism component is neutralized by rigid contact lenses. This finding is more common among older patients and often explains why their hard contact lenses fail to provide the anticipated vision correction. These cases can be identified via spherocylinder refraction over the contact lens. However, against-the-rule lenticular astigmatism is probably present when against-the-rule refractive astigmatism (adjusted to reflect the power at the corneal surface) exceeds the keratometric corneal astigmatism. Such eyes may have less residual astigmatism when the refractive error is corrected with soft rather than rigid spherical contact lenses if the corneal astigmatism is compensating for lenticular astigmatism.
For example, consider a patient whose refraction is –3.50 –0.50 × 180 and K measurements of the affected eye are 42.5 D (7.94 mm) horizontal and 44.0 D (7.67 mm) vertical. Would a soft or rigid contact lens provide better vision (ie, less residual astigmatism)? The disparity between the corneal astigmatism of 1.50 D and the refractive astigmatism of 0.50 D reveals 1.00 D of against-the-rule lenticular astigmatism that neutralizes a similar amount of with-the-rule corneal astigmatism. Neutralizing the corneal component of the refractive astigmatism with a rigid contact lens exposes the lenticular residual astigmatism. Therefore, a spherical soft contact lens would provide better vision because the residual astigmatism is 1.00 D for a rigid contact lens.
Correcting Presbyopia
Correcting presbyopia with contact lenses can be done in several different ways:
- reading glasses over contact lenses
- alternating vision contact lenses (segmented or annular)
- simultaneous vision contact lenses (aspheric [multifocal] or diffractive)
- monovision
From an optical point of view, the use of reading glasses or alternating vision contact lenses is similar to standard spectacle correction for presbyopia. Simultaneous vision contact lenses direct light from 2 points in space—one near, one far—to the retina, resulting in a loss of contrast. Distant targets are “washed out” by light coming in through the near segment(s), and near objects are “washed out” by light coming in through the distance segment(s). Monovision allows one eye to have better distance vision and the other to have better near vision, but this arrangement interferes with binocular function, and the patient then has reduced stereopsis. For these reasons, it is important to fully explain the options to contact lens wearers with presbyopia. As previously demonstrated, it is important to explain to a new contact lens wearer with presbyopia and myopia that he or she may need near correction or one of the other aforementioned options when presbyopic correction with the spectacles had not previously been required. The contact lens correction of presbyopia is discussed in greater detail in the section Contact Lenses for Presbyopia.
Kastl PR, ed. Contact Lenses: The CLAO Guide to Basic Science and Clinical Practice. 4 vols. Dubuque, IA: Kendall-Hunt; 1995.
Contact Lens Materials and Manufacturing
Various materials have been used to make contact lenses. The choice of material can affect contact lens parameters such as wettability, oxygen permeability, and deposits on the lens. In addition, material choice affects the flexibility and comfort of the lens and the stability and quality of vision. Manufacturing techniques primarily address the ability to make reproducible lenses in a cost-effective manner.
Materials
Contact lens materials can be described in terms of flexibility (hard, rigid gas-permeable [RGP], soft, or hybrid). The first popular corneal contact lenses were made of PMMA, a plastic that is durable but not oxygen permeable. Gas-permeable materials are rigid but usually more flexible than PMMA. RGP lenses allow some oxygen permeability (Dk); this factor may vary from Dk 15 to more than Dk 100. This feature has allowed some RGP lenses to be approved for overnight or extended wear. Currently, most RGP lenses are made of silicone acrylate. This material provides the hardness needed for sharp vision, which is associated with PMMA lenses, and the oxygen permeability associated with silicone. Despite advances, wettability still poses a challenge (Fig 4-7).
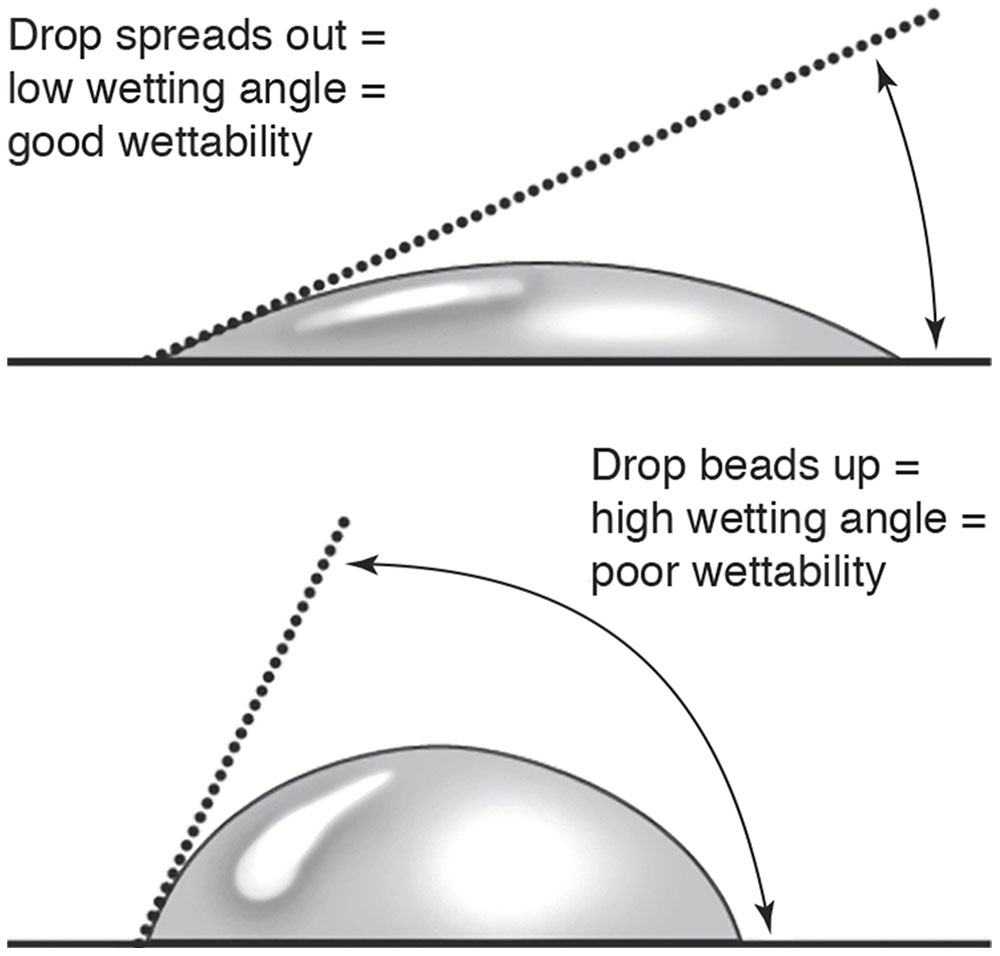
Figure 4-7 The wettability of a lens surface determines whether a wetting angle will be low (greater wettability, greater comfort) or high (less wettability, less comfort). (Modified with permission from Stein HA, Freeman MI, Stein RM. CLAO Residents Contact Lens Curriculum Manual. New Orleans: Contact Lens Association of Ophthalmologists; 1996. Redrawn by Christine Gralapp.)
The newest lenses are made of fluoropolymer, which provides greater oxygen permeability than does PMMA. Disadvantages of fluoropolymer lenses are rigidity and discomfort.
The gas permeability of a material is related to (1) the size of the intermolecular voids that allow the transmission of gas molecules, and (2) the gas solubility of the material. Silicon monomers are the most commonly used materials because their characteristic bulky molecular structure creates a more open polymer architecture. The addition of fluorine increases the gas solubility of polymers and somewhat counteracts the tendency of silicon to bind hydrophobic debris (such as lipid-containing mucus) to the contact lens surface. In general, polymers that incorporate more silicon offer greater gas permeability at the expense of surface biocompatibility.
Soft contact lenses are typically made of a soft hydrogel polymer, hydroxyethylmethacrylate. The surface characteristics of hydrogels can change instantaneously, depending on their external environment. When hydrogel lenses are exposed to water, their hydrophilic elements are attracted to (and their hydrophobic components are repelled from) the surface, which becomes more wettable. However, drying of the surface repels the hydrophilic elements inward, making the lens surfaces less wettable. The hydrophobic surface elements have a strong affinity for nonpolar lipid tear components through forces known as hydrophobic interactions. Such interactions further reduce surface wettability, accelerate evaporative drying, and compromise the clinical properties of soft lenses.
The oxygen and carbon dioxide permeability of traditional hydrogel polymers is directly related to their water content. Because tear exchange under soft lenses is minimal, corneal respiration depends almost entirely on the transmission of oxygen and carbon dioxide through the polymer matrix. Although the oxygen permeability of hydrogel polymers increases with water content, so does their tendency to dehydrate. To maintain the integrity of the tear compartment and avoid corneal epithelial desiccation in dry environments, these lenses are made thicker, thereby limiting their oxygen transmissibility.
High-oxygen-permeability, low-water-content silicone hydrogels are used for extended wear. The oxygen transmission of these lenses is a function of their silicon (rather than water) content and is sufficient to meet the oxygen needs of most patients’ corneas during sleep. The surfaces of these lenses require special coatings to mask their hydrophobic properties. Other clinically important properties of contact lens hydrogels include light transmission, modulus (resistance to flexure), rate of recovery from deformation, elasticity, tear resistance, dimensional sensitivity to pH and the osmolality of the soaking solution and tears, chemical stability, deposit resistance, and surface water-binding properties.
Manufacturing
Several methods are used to manufacture contact lenses. Some contact lenses are spin-cast, a technique popularized with the first soft contact lenses. In spin-casting, the liquid plastic polymer is placed in a mold that is spun on a centrifuge; the shape of the mold and the rate of spin determine the final shape of the contact lens. Soft contact lenses can also be made on a lathe, starting with a hard, dry plastic button; this method is similar to the way that RGP lenses are made. Once the soft lens lathe process is complete, the lens is hydrated in saline solution to create the characteristic softness. Lathes may be either manually operated or automated. In either case, manufacturers can create very complex, variable shapes that provide correction for many different types of refractive error; lenses can even be customized to meet individual needs.
Following the introduction of disposable contact lenses—and thus the need to manufacture large quantities of lenses—cast molding was developed. In this technique, different metal dies, or molds, are used for specific refractive corrections. Liquid polymer is injected into the mold and then polymerized to create a soft contact lens of the desired dimensions. This process is completely automated from start to finish, enabling cost-effective production of large quantities of lenses.
Scleral contact lenses have very large diameters and touch the sclera 2–4 mm beyond the limbus. They have been available for years, but because they were originally made of PMMA—and thus were oxygen impermeable—the lenses were not comfortable. With the use of newer RGP materials, interest in these lenses has resurfaced, especially for patients with abnormal corneas. Scleral contact lenses are made from a mold taken of the anterior surface of the eye; the mold is made of an alginate mix, which hardens in the shape of the ocular surface. This alginate mold is then used to make a plaster mold, which, in turn, is used to make the actual scleral lens.
Patient Examination and Contact Lens Selection
As in all patient care, a complete history and eye examination are needed to rule out serious ocular problems such as glaucoma and macular degeneration.
Patient Examination
A clinician needs specific information to select a contact lens for a particular patient. This information includes the patient’s daily activities (desk work, driving, and so on) and reason for using contact lenses (eg, full-time vision, sports only, social events only, changing eye color, avoiding use of reading glasses). If a patient is already a contact lens user, the fitter must also find out the following: the number of years the patient has worn contact lenses, the current type of lens worn, the wear schedule, and the care system used. In addition, the fitter must determine whether the patient currently has or previously had any problems with lens use.
Factors that may suggest an increased risk of complications with contact lens use include diabetes mellitus, especially if uncontrolled; immunosuppression; long-term use of topical medications such as corticosteroids; and environmental exposure to dust, vapors, or chemicals. Other relative contraindications to contact lens use include an inability to handle and/or care for contact lenses; monocularity; abnormal eyelid function, such as with Bell palsy; severe dry eye; and corneal neovascularization. The primary indications for contact lenses in a patient with preexisting corneal disease are therapeutic or bandage lenses and a rigid contact lens for the correction of irregular astigmatism.
Key areas to observe during slit-lamp examination include the eyelids (to rule out blepharitis or mechanical lid abnormalities such as trichiasis, ectropion, and entropion), the tear film, and the ocular surface (to rule out dry eye). Eyelid movement and blink should also be observed. The cornea and conjunctiva should be evaluated carefully for signs of ocular surface disease, allergy, scarring, symblepharon, or other signs of conjunctival scarring diseases, such as ocular cicatricial pemphigoid (mucous membrane pemphigoid). Through refraction and keratometry, the ophthalmologist can determine whether there is significant corneal, lenticular, or irregular astigmatism. The identification of irregular astigmatism may suggest other pathologies, such as keratoconus, that would require further evaluation.
Contact Lens Selection
The selection of a contact lens for an individual patient and eye is a complex process. Optical, biological, mechanical, and social considerations are among the factors that enter into this process (see Table 4-1).
Soft contact lenses are currently the most frequently prescribed and worn lenses in the United States. They can be classified according to various characteristics. Given this variety, selection of the appropriate lens for each patient may be difficult. Typically, an experienced fitter knows the characteristics of several lenses that cover the needs of most patients.
The main advantages of soft contact lenses are their shorter period of adaptation and their high level of comfort (Table 4-3). They are available with many parameters so that all regular refractive errors are covered. Furthermore, the ease of fitting soft lenses makes them the first choice of many practitioners.



