Fig. 20.1
Typical output properties of a swept laser. (a) Tuning curve. (b) Time trace. (c) Spectrum. (d) Coherence. The definition of each parameter is described in the text
Sweep repetition rate. Figure 20.1b illustrates an exemplary time trace of laser output power that corresponds to a Gaussian-like tuning spectrum shown in Fig. 20.1c. The sweep repetition rate, a reciprocal of sweep period, determines the A-line acquisition rate in OCT. A higher A-line rate can increase frame rate, reduce motion artifacts, and allow screening over a larger tissue surface in a limited time. For these reasons, A-line rates greater than 20 kHz would be required in most clinical applications. On the other hand, the limited bandwidth and data handling speed of currently available hardware put a practical limit on the maximum achievable A-line rate in a system. Depending on applications and system capability, the sweep repetition rate of a source may need to be between 20 and 200 kHz.
Center wavelength (λ 0 ). The optimal center wavelength is somewhat dependent upon the sample and application. Longer wavelengths are less scattered and can penetrate deeper in tissue, but absorption, dominantly by water, has a strong wavelength dependence [2]. In general, there are two distinct spectral windows for imaging. The first window (650–900 nm) is suitable for retinal imaging because of low absorption in vitreous humor. This range can be extended to 1,100 nm where the penetration depth in the retina and choroid is increased. The second window in 1,100–1,360 nm permits even deeper tissue penetration and, therefore, is suitable for most non-ophthalmic imaging. Certainly, other wavelengths, such as visible or beyond 1,500 nm, have potential for specific applications, such as molecular contrast-based imaging or non-biological material with low water concentration.
Tuning range (Δλ). Figure 20.1c depicts an exemplary output spectrum with a truncated Gaussian-like profile, typical of swept lasers. The spectral envelope is related to the point spread function through the Fourier transform, although windowing can be applied in data processing. The tuning range is defined from edge to edge (full range), at –3 dB (full width at half maximum: FWHM), or at 1/e2 level. Assuming a Gaussian spectrum with 1/e2 width of Δλ, the axial resolution, defined as the FWHM of point spread function, is given by
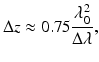
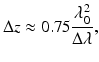
(20.1)
As numerical examples, a tuning range of Δλ = 127 nm at λ0 = 1,300 nm yields Δz = 10 μm; the same resolution is achieved with Δλ = 48 nm at λ 0 = 800 nm.
Instantaneous linewidth (δλ). The laser emits a narrowband spectrum instantaneously. The finite linewidth of the instantaneous output causes the visibility of interference to decrease with path length difference, as illustrated in Fig. 20.1d. The coherence function is related to the instantaneous spectrum through the Fourier transform, just like the point spread function is to the overall tuning spectral envelope. The coherence length is defined as the optical delay when interference visibility drops to 0.5. This corresponds to a full depth range with visibility greater than >0.5. Because SNR is proportional to the square of the visibility, longer coherence length is required in OCT. The coherence length, z c, is related to the FWHM instantaneous linewidth, δλ, via
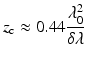
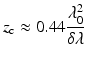
(20.2)
Most OCT applications require a depth range between 2 and 6 mm. Given that positive and negative depths are indistinguishable in normal OCT, a coherence length of 4–12 mm would be required. As a numerical example, δλ = 0.1 nm at λ 0 = 1,300 nm yields z c = 7.4 mm; the same coherence length is obtained with δλ = 0.038 nm at λ 0 = 800 nm.
Intensity noise. Intensity fluctuations of laser output, if they have significant frequency components in the signal detection band, can degrade SNR and may produce image artifacts through frequency mixing with signals. Mechanical vibration and noisy pump sources are two primary sources for 1/f-type intensity noise. Mode partition noise or mode beating noise occurs at the fundamental frequency equal to the reciprocal of the cavity roundtrip time or its harmonics. In swept lasers, multiple path interference due to spurious back reflections in intracavity components or the gain chip can cause intensity modulation at frequencies corresponding to path differences. In OCT detection, the total intensity noise should be smaller than shot noise [3], given as 〈ΔP r 2〉 < 2 hv P r where 〈ΔP r 2〉 is the time-averaged intensity noise power per a 1 Hz bandwidth, hv is a single photon energy (h is Planck’s constant), and P r is the average reference power. The noise power per bandwidth is conveniently characterized with relatively intensity noise (RIN) that is defined as
![$$ \mathrm{R}\mathrm{I}\mathrm{N}=\frac{<\Delta {P}^2>}{P^2}\kern0.1em \left[H{z}^{-1}\right] $$
” src=”/wp-content/uploads/2017/03/A76297_2_En_21_Chapter_Equ3.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(20.3)</DIV></DIV></DIV><br />
<DIV class=Para>Therefore, the shot-noise limit condition is reduced to RIN < 2 <SPAN class=EmphasisTypeItalic>hv</SPAN>/<SPAN class=EmphasisTypeItalic>P</SPAN> <SUB><SPAN class=EmphasisTypeItalic>r</SPAN> </SUB>. Typically, <SPAN class=EmphasisTypeItalic>P</SPAN> <SUB><SPAN class=EmphasisTypeItalic>r</SPAN> </SUB>= 10–100 μW, and therefore, RIN <−135 – −145 dB/Hz. This is achievable in swept lasers. The RIN spectrum of a laser output can be measured with a photodiode and an electrical spectrum analyzer. In an OCT system, the effect of the laser RIN can be reduced by 15–30 dB using dual balanced detection.</DIV><br />
<DIV class=]() Output polarization. Single polarization output is ideal. With a dual polarization source, polarization-dependent delay in the interferometer, such as polarization mode dispersion in a circulator, can cause blurry images. Even when the source output is singly polarized, the specific polarization state may vary as a function of wavelength in a swept laser, particularly if the cavity has strong birefringence. This wavelength dependence should be minimized, because it can lead to an intensity modulation through polarization-dependent loss or splitting ratio in the interferometer or probe optics, resulting in image artifacts.
Output polarization. Single polarization output is ideal. With a dual polarization source, polarization-dependent delay in the interferometer, such as polarization mode dispersion in a circulator, can cause blurry images. Even when the source output is singly polarized, the specific polarization state may vary as a function of wavelength in a swept laser, particularly if the cavity has strong birefringence. This wavelength dependence should be minimized, because it can lead to an intensity modulation through polarization-dependent loss or splitting ratio in the interferometer or probe optics, resulting in image artifacts.




Get Clinical Tree app for offline access
Miscellaneous. A small-sized mechanically durable light source would be highly desirable if it is to be integrated into a compact, portable system for space-limited clinical environment. Long-term reliability and stability are highly desirable for clinical or industrial uses.
20.3 Fundamentals
A laser is an optical oscillator, coined after its underlying physical mechanism: light amplification by the stimulated emission of radiation. Central to laser instrumentation is a gain medium where light is amplified. Another fundamental component is an optical cavity that gives coherent optical feedback for laser oscillation. The optical cavity also provides space to insert other various optical components, such as lenses, nonlinear optical materials, and spectral filters. These intracavity components are used to condition temporal and spectral characteristics of laser light to specific purposes. For example, an intracavity tunable filter is widely used in a tunable laser. In this section, we describe some fundamentals of lasers and their wavelength sweep operation.
20.3.1 Gain Medium
A gain medium that is pumped to reach an electronic population inversion is able to amplify optical energy. Figure 20.2a illustrates this principle with regard to a semiconductor [4]. The valence and conduction bands serve as the ground and excited state. A positive bias is applied to the semiconductor so that injected electrons flow into the conduction band and populate it, whereas holes are created in the valence band. An incoming photon, if its energy is equal to the energy difference between the two bands, can trigger the transition of an excited electron to the valence band, where it is recombined with a matching hole. In this stimulated transition process, the energy difference is radiated optically, resulting in the emission of a new photon that has identical energy, phase, and propagation direction compared with the original photon. This process, called stimulated emission, is the fundamental mechanism for coherent optical amplification. Other types of gain media, such as gas, dyes, crystals, and glass, are based on the same mechanism, although specifics of the transition levels of electrons and pumping methods are different. Gain saturation, or a decrease of gain due to the depletion of population inversion by strong optical intensity, is an intrinsic characteristic of gain media. In typical laser oscillation at the steady state, gain is saturated substantially to a level where the saturated gain is just enough to compensate for the loss in a laser cavity.


Fig. 20.2
Semiconductor optical amplifier. (a) The principle of light amplification in semiconductor. (b) A schematic of quantum-well amplifier. Light is guided and amplified in the active region
20.3.1.1 Semiconductor Optical Amplifier (SOA)
Figure 20.2b shows a schematic of an SOA. SOAs are one of the most widely used gain media for rapidly swept lasers for several reasons. First, the flexibility of semiconductors in making heterogeneous structures offers a wide range of gain center wavelengths. SOAs are typically made from group III–V compound semiconductors such as GaAs/Al x Ga 1–x As (λ0 = 0.75–0.9 μm) and In1−x Ga x As1−y P y /InP (λ0 = 1.1–1.6 μm).
Second, an SOA offers high gain with broad bandwidth. This gives a great flexibility in choosing a filter and cavity configuration for wide range and fast tuning. The high gain of an SOA, typically 20–35 dB, comes in part from its waveguide structure that ensures a long active region, typically 300–1,000 μm. Gain bandwidth, depending on the specific semiconductor materials, chip designs, and the inversion level, can be greater than 10 % of the center wavelength.
Third, the gain response time of an SOA is about 250 ps, much shorter than the micro- or millisecond timescale of other gain media, such as a titanium-sapphire and rare-earth-doped fibers. For fast sweep operation, the short gain response time is highly desirable to minimize the intensity noise of the laser output. With a slow gain medium, even a small magnitude of cavity loss modulation associated with filter sweep can interplay resonantly with gain recovery and lead to self Q-switching or relaxation oscillation [5]. For solid-state gain media, this resonance is typically in the frequency range between 1 kHz and 1 MHz, which becomes a serious problem because it may overlap with the signal band used for imaging. A similar type of intensity modulation can arise in a semiconductor laser, but the modulation frequency is in the GHz range, and it can be easily removed electrically without affecting the signals.
20.3.2 Laser Cavity
A laser cavity is a resonator that gives phase-coherent optical feedback for regenerative amplification in the gain medium [5]. A variety of optical materials and components can be incorporated into a cavity to control and condition the characteristics of a laser. By its geometrical shape, a laser cavity can be categorized into a linear, ring, or hybrid (such as sigma) type. In a linear cavity, exemplified in Fig. 20.3a, intracavity light passes through a gain medium and a transmissive filter twice in each round trip. A ring cavity is often made unidirectional, ensured by a magneto-optic isolator with a direction-dependent insertion loss. The unidirectional ring cavity offers a distinct advantage that the backward reflected light from intracavity components is de-coupled from the main beam path and as a result, often produces more stable laser oscillation than a linear cavity. This advantage may not be evident, however, in most rapidly swept lasers that are less sensitive to the spurious feedback due to oscillation of multiple longitudinal modes.
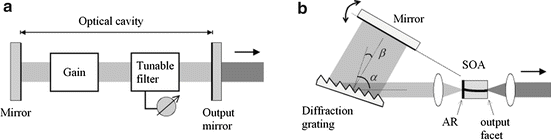

Fig. 20.3
Tunable laser. (a) Basic configuration. (b) A schematic of typical external-cavity semiconductor tunable laser. AR anti-reflection coating, SOA semiconductor optical amplifier
Longitudinal cavity modes are a set of frequency components capable of oscillating resonantly in the cavity. Each mode satisfies the resonance condition that the total optical phase accumulated in one roundtrip propagation is equal to an integer multiple of 2π. The frequency difference between two adjacent modes, or the mode spacing f m , is given by
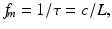
where τ is the total propagation time of cavity roundtrip and L is the total optical length that includes group refractive indices of the cavity.
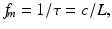
(20.4)
The laser output is obtained through an output coupler of the cavity. Large output coupling can extract larger optical energy from the cavity, thus resulting in a higher output power, but may decrease the tuning range due to resulting increased cavity loss. An optimum output coupling ratio can be chosen with some trade-off in performance, ranging from a few percent in low-gain lasers, such as a titanium-sapphire laser, to several tens of percents in high-gain lasers, such as a semiconductor or rare-earth-doped fiber laser.
20.3.3 Tunable Laser
Wavelength-tunable lasers have developed considerably since the mid-1960s and are now invaluable light sources for numerous scientific and industrial applications. Figure 20.3a represents a schematic of a tunable laser configuration consisting of a broadband gain media, an optical cavity, and a narrowband tunable filter. To illustrate the basic principle of a tunable laser, let us consider an extended-cavity semiconductor lasers, one of the most versatile and commercially successful tunable sources. Figure 20.3b depicts a representative schematic of the laser. One facet of a semiconductor gain chip serves as a partial reflector and output coupler of a laser cavity. Partial reflectance is normally achieved just by cleaving the facet perpendicular to the optic axis, yielding Fresnel reflection by 26–30 % for typical semiconductor materials. Optical reflection at the other facet of the chip is minimized to <0.001 % by anti-reflection dielectric coating (R = 0.1 %) and the curved active waveguide design. At the other end of the cavity, a diffraction grating and a mirror serve as a tunable wavelength selective filter. The angular position of the mirror determines the specific wavelength component that returns to the gain medium via [6]
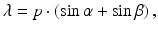
where p denotes the grating pitch, α is the angle between the grating normal and beam incidence axis, and β is the angle between the grating normal to the diffracted beam as determined by the angular position of the end mirror. The reflected spectrum of the grating filter has a narrowband Gaussian-like profile with a width approximately given by λ/N where N denotes the number of grooves illuminated by the optical beam on the grating.
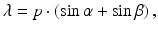
(20.5)
Figure 20.4a depicts the resulting net-gain profile together with the spectrum of oscillating laser modes. The gain profile has a peak at the wavelength determined by Eq. 20.5. The net roundtrip gain becomes close to one in steady-state laser oscillation. Because of the strong gain discrimination by the filter, only the frequency mode closest to the gain peak is able to oscillate. Single-frequency oscillation offers a very narrow linewidth of <100 kHz and a long coherence length exceeding 10 km, typical of an extended-cavity semiconductor laser.
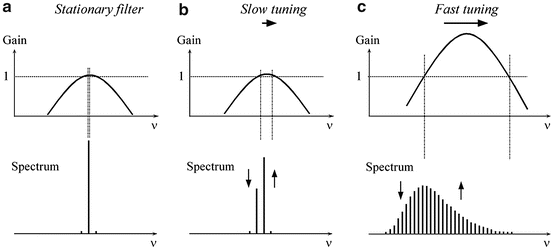

Fig. 20.4
Spectral dynamics in a tunable laser. The net-gain profile and oscillating mode spectrum are illustrated in three distinct cases: (a) fixed-wavelength filter and single-frequency oscillation, (b) slowly tuned filter and mode hopping, and (c) rapidly swept filter and multiple mode oscillation
20.3.4 Sweep Operation
By rotating the end reflector, the gain peak wavelength can be shifted continuously, and the output spectrum can be swept accordingly [7]. Figure 20.4b illustrates this situation in the case of slow adiabatic tuning where steady-state oscillation is reached at any given time. Here, the cavity length is assumed invariant so that the positions of cavity modes are stationary in the frequency domain. Under this condition, as the gain profile is continuously shifted by tuning, the laser spectrum steps from one mode to another – a process called mode hopping.
In some applications such as high-resolution atomic spectroscopy, truly continuous tuning without mode hopping is desirable. The extended-cavity tunable laser shown in Fig. 20.3b offers a simple way to achieve this feature. The underlying idea is to vary the cavity length in conjunction with tuning, such that the frequency of a cavity mode always coincides with the gain peak frequency. This can be achieved by placing the pivot point of the end mirror exactly at the output facet of the gain chip. Using this geometrical arrangement [8], commercial extended-cavity tunable lasers can produce a mode-hop-free sweep over several tens of nanometers. However, their tuning speeds currently are limited to <1 nm/ms, although the technique can work in principle at an arbitrary sweep speed.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


