is an associate professor of ophthalmology at the Cullen Eye Institute, Department of Ophthalmology, Baylor College of Medicine. Her areas of research include various aspects in cataract surgery, refractive surgery, diagnostic devices, optics, and wavefront technology and its use in refractive and cataract surgery.


is an associate professor at the Cullen Eye Institute, Baylor College of Medicine, where he specializes in corneal, cataract, and refractive surgery. His research interests include biomedical optics, anterior segment imaging, intraocular lens technology, and wavefront applications in cataract and refractive surgery. He is the residency program director at the Cullen Eye Institute, Baylor College of Medicine, and the medical director of the Lion’s Eye Bank of Texas.


is professor and the Allen, Mosbacher, and Law Chair in ophthalmology at the Cullen Eye Institute, Baylor College of Medicine, where he specializes in cataract and refractive surgery. His research interests include optics of cataract and refractive surgery, intraocular lens technology, anterior segment imaging, and surgical techniques in cataract and refractive surgery. He is Editor Emeritus of the Journal of Cataract and Refractive Surgery and past president of the American Ophthalmological Society, American Society of Cataract and Refractive Surgery, and International Intraocular Implant Club.


5.1 Introduction
Compared with current accuracy standards for virgin eyes, determining intraocular lens (IOL) power for eyes that have had corneal refractive surgery is difficult [1–3]. IOL power errors in these eyes can be attributed primarily to 2 factors: inaccurate determination of the true total corneal refractive power and incorrect estimation of the effective lens position (ELP) by those third- or fourth-generation IOL power calculation formulas that use corneal powers when calculating ELP [4, 5].
Various methods have been proposed to improve the accuracy of IOL power calculation after corneal refractive surgery. To facilitate this process, Hill, Wang, and Koch developed an internet-based IOL power calculator that can be accessed through the American Society of Cataract and Refractive Surgery (ASCRS) web site (ascrs.org). This online calculator has three categories of formulas: (1) IOL power calculation for eyes with previous myopic LASIK or PRK, (2) IOL power calculation for eyes with previous hyperopic LASIK or PRK, and (3) IOL power calculation for eyes with previous radial keratotomy (RK).
Using the ASCRS online calculator, Wang et al. [6] evaluated the accuracy of methods of IOL power prediction after previous laser in situ keratomileusis (LASIK) or photorefractive keratectomy (PRK). The study compared the following methods: those using pre-LASIK/PRK keratometry and surgically induced change in refraction (so-called “clinical history” methods), methods using surgically induced change in refraction, and methods using no previous data. The predicted IOL power was calculated with each method targeting the post-cataract surgery refraction. The IOL prediction errors were calculated and analyzed. The study found that IOL calculation methods using surgically induced change in refraction and methods using no previous data had smaller mean absolute IOL prediction errors, smaller variances, and greater percentage of eyes within an acceptable range of refractive prediction errors than methods using pre-LASIK/PRK keratometry values and surgically include change in refraction.
With post-refractive surgery IOL power calculations now more accessible via the ASCRS calculator, there have been ongoing investigations into the use of novel technologies to yield more accurate measurements of the cornea. Direct measurement of the posterior corneal power is a promising solution for calculating IOL power after previous laser vision correction. Slit-scanning tomography, rotating-slit Scheimpflug camera, and dual-Scheimpflug systems have been used for this purpose [7–9]. However, the axial (depth) resolutions of these devices are between 50 and 100 μm due to the diffraction limit. This relatively poor resolution can lead to errors in the delineation of the posterior corneal border in the presence of corneal haze or opacity, a problem that is well documented for slit-scanning tomography [10–13].
Optical coherence tomography (OCT) has been proposed as a more accurate method for measuring total corneal power [14, 15]. The higher axial resolution of OCT (3–17 μm in commercial instruments) allows clear delineation of corneal boundaries, even in the presence of opacities [10]. With the recent advance from time-domain to frequency-domain detection, the speed of OCT corneal mapping is now faster than that of slit-scanning or Scheimpflug-based devices. Based on these theoretical advantages, OCT may be a promising technology in this application.
Two prior studies report the development of an OCT-based formula to refine IOL power prediction in post-LASIK eyes [16, 17]. A third study used this OCT-based formula to evaluate the accuracy of IOL power calculation in eyes with prior radial keratotomy (RK). The study found that the OCT-based IOL power calculation is a promising option for calculating IOL power in post-RK eyes and that the adjusted effective corneal power (ECP) formula reduces overall hyperopic surprises and yields higher consistency in IOL prediction [18].
In a recent study, Wang et al. validated the OCT-based IOL power formula and compared it to the methods of the ASCRS calculator in eyes with previous myopic LASIK or PRK. Their preliminary findings, which were presented at ASCRS 2013, are discussed below [19].
5.2 Methods
5.2.1 OCT-Based Power Calculation
Between November 2010 and March 2012, Wang et al. [19] prospectively enrolled patients undergoing cataract surgery with monofocal IOL implantation who had previous myopic laser vision correction. A spectral domain OCT system (RTVue, Optovue Inc.) was used to measure anterior, posterior, and net corneal powers and central corneal thickness (CCT).
The OCT-based IOL power formula was previously described [16]. It used an eye model consisting of four optical surfaces: the anterior corneal surface, posterior corneal surface, IOL, andthe retina. The IOL was modeled as a thin lens. The OCT net corneal power was converted to an effective corneal power (ECP) for insertion into the IOL formula as follows:

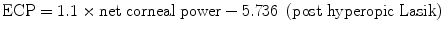

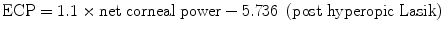
These equations were generated from a linear regression analysis of ECPs that were back-calculated from the postoperative manifest refraction spherical equivalent (MRSE), preoperative ACD, preoperative AL, preoperative posterior corneal power (from OCT), and preoperative CCT (from OCT) [17].
The ASCRS online IOL calculator was used for those formulas for which pertinent data were available. To use the IOL calculator (ascrs.org), all available data before and after LASIK or PRK and the measurements before cataract surgery are entered. The “calculate” button is then clicked, and the results are shown at the bottom of the form (Fig. 5.1).
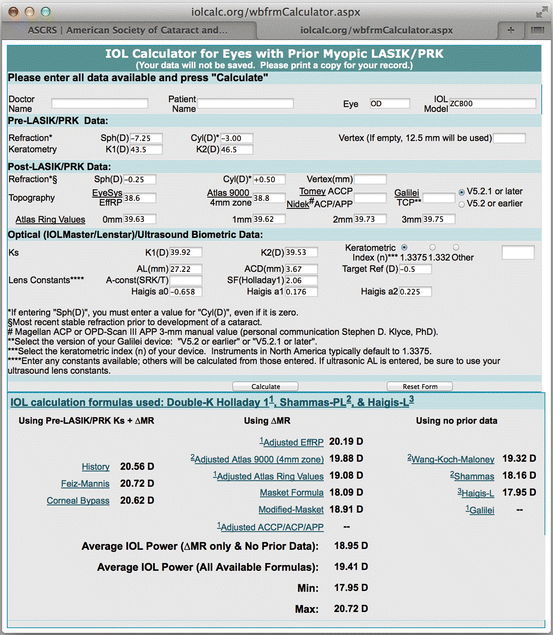

Fig. 5.1
Online IOL calculator for eyes with previous myopic LASIK or PRK
The predicted IOL power was calculated with each method using the actual postoperative refraction as the target. The IOL prediction error was calculated as the implanted IOL power minus the predicted IOL power. The refractive prediction error was calculated by assuming that 1 D of IOL prediction error produces 0.7 D of refractive error. Mean absolute refractive prediction error (MAE) was calculated after adjusting the mean numerical prediction error to zero. Percentages of eyes with 0.5 D and 1.0 D of refractive prediction error were also determined.
5.2.2 Statistical Analysis
For the OCT analysis, the Wilcoxon signed-rank test for paired samples was used to compare the MAEs and adjusted MAEs of refractive prediction between different IOL formulas. The Fisher exact probability test was used to compare the proportion of eyes within 1.0 D of predicted refraction. A P-value of less than 0.05 was considered statistically significant.
5.3 Results
Twenty-eight eyes of 24 patients with previous myopic LASIK or PRK undergoing cataract surgery were enrolled in the study. The mean age at the time of surgery was 62 ± 7 years (SD) (range 46 to 75 years). Fourteen eyes had historic data available; for these eyes, the mean magnitude of previous myopic correction was −5.02 ± 2.91 D (range −0.88 to −11.13 D).
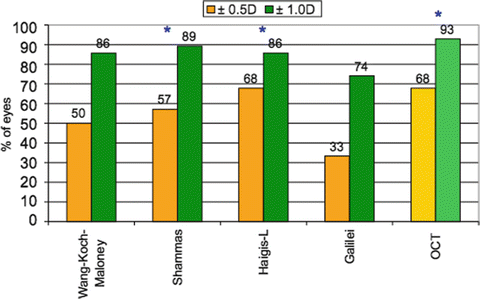
For methods using no prior data (n = 28), the study found that OCT had a significantly lower refractive mean absolute error (MAE) than the Galilei (0.43 D vs. 0.74 D, P < 0.05) (Fig. 5.2). The Shammas and the Haigis-L were also significantly lower than the Galilei.


Fig. 5.2
Refractive MAE with methods using no prior data (n = 28). Significantly greater MAE with Galilei than those with OCT, Shammas, and Haigis-L (all P < 0.05)
The OCT formula, Haigis-L, and Shammas formulas had significantly more eyes within ±1.0 D of refractive prediction errors, compared to the Galilei formula (all P < 0.05). (Fig. 5.3).