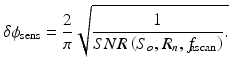Fig. 40.1
Phase contrast microscopy. Brightfield (left) and phase contrast (right) images of a diatom. These are the oldest phase contrast micrographs from Zernike and were taken in 1932 (Figure from Zernike [1])
Phase contrast microscopy has had an immeasurable impact by allowing the user to qualitatively visualize small, subcellular variations in optical index. Quantitative phase microscopy seeks to build upon the principles of Zernike to extract information relating to optical index, birefringence, motion, and flow. In addition to highlighting subcellular detail in unstained cells, quantitative phase techniques can measure small cell motions, small changes in cell index, and cytoplasmic flow.
Because of its sensitivity to phase and its ability to reliably quantify and track changes in coherent wavefronts, interferometry has recently gained momentum as a technique for the implementation of quantitative phase microscopy. This chapter seeks to review several of these interferometric techniques, with an emphasis on broadband interferometric techniques which exploit the principles of OCT. Both the underlying theory as well biological applications are discussed. Although this chapter gives particular focus to biologically relevant applications, the methods are readily extendable for other, nonbiological applications.
40.1.2 Definition of Interferometric Phase
When discussing coherent wavefields, it is usual to represent the wavefield as a complex function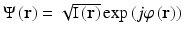 
, where r is a vector representing three-dimensional position, I(r) is the intensity of the wave, and φ(r) the phase of the field [2]. This representation is convenient for several reasons. The surfaces of constant φ(r) represent wavefronts, while ∇φ(r) describes the free-space propagation direction [2]. This definition decouples temporal and spatial variation in the field: the time-varying wavefunction is given by exp(j2πνt)Ψ(r), where ν is the frequency of the field. If Ψ(r) is a one-dimensional wave propagating in a medium of uniform index n, φ(r) can be represented as φ(x) = nkx + φ o, where k is the free-space wavenumber (2π/λ; λ = free-space wavelength), x is the spatial coordinate in the direction of propagation, and φ o is the initial or reference phase of the field. φ o is analogous to a reference electrical potential insofar as both phase and potential are relative measurements.
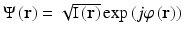, where r is a vector representing three-dimensional position, I(r) is the intensity of the wave, and φ(r) the phase of the field [2]. This representation is convenient for several reasons. The surfaces of constant φ(r) represent wavefronts, while ∇φ(r) describes the free-space propagation direction [2]. This definition decouples temporal and spatial variation in the field: the time-varying wavefunction is given by exp(j2πνt)Ψ(r), where ν is the frequency of the field. If Ψ(r) is a one-dimensional wave propagating in a medium of uniform index n, φ(r) can be represented as φ(x) = nkx + φ o, where k is the free-space wavenumber (2π/λ; λ = free-space wavelength), x is the spatial coordinate in the direction of propagation, and φ o is the initial or reference phase of the field. φ o is analogous to a reference electrical potential insofar as both phase and potential are relative measurements.Interferometry is a powerful, although by no means the only [2], technique for retrieving the phase of coherent wavefields. The interferometric signal is complex in nature and can be related to the linear difference between the sample and reference arm phase functions φ S (x) and φ R (x). If both arms are free space (i.e., n = 1), then φ S(x) − φ R(x) reduces to 2kΔx, where Δx is the free-space path length difference between the two arms (Fig. 40.2). One insight that can be drawn from this representation is that small displacements of the sample reflector can be monitored by holding the reference arm fixed and measuring the phase of the interferometric signal versus time. This is a powerful technique limited by the stability of the reference reflector.
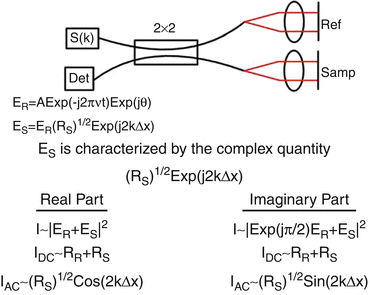
Fig. 40.2
Definition of the complex interferometric signal illustrated in a 2 × 2 50/50 Michelson topology. S(k) represents a monochromatic source. The free-space path length difference between the reference and sample arms is Δx. At the detector the reference electric field is characterized by an amplitude A which incorporates the reference arm reflectivity RR and the double-pass attenuation in the 2 × 2, a time-varying component (ν, optical frequency), and a phase θ which incorporates the initial phase of the light out of the source and phase accumulated in the interferometer. The sample field is an attenuated and phase-shifted version of the reference field. It is attenuated by the square root of the sample reflectivity and phase shifted by twice the product of the path length difference Δx between the reference and sample reflectors and the optical wavenumber k. When mixed at a square-law detector, the real (cosinusoidal) part of the complex interferometric electric field is measured. One method to gain access to the imaginary (sinusoidal) part of the field is to phase shift the reference field by π/2 rad with respect to the sample field
The phase of the interferometric signal is sensitive to changes in optical index as well. Consider the setup in Fig. 40.3. The free-space path length of both arms are identical, but the sample arm has two compartments: one free-space compartment of path length x and another compartment of length x n with a time-varying index n(t). The interferometric phase φ S(x) − φ R(x) is now related to the index by 2kx n [n(t)−1]. Since the index of an aqueous solution is proportional to its osmolarity, this suggests a method for monitoring changes in solution osmolarity by tracking the interferometric phase.
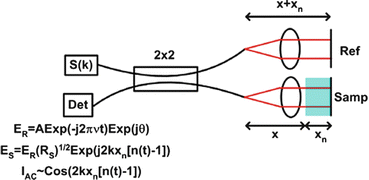
Fig. 40.3
Relationship of interferometric phase to changes in optical index
Just as changes in index and in path length can be monitored by measuring interferometric phase, changes in sample arm wavenumber can likewise be monitored. The sample field frequency can be changed by reflection from a moving reflector or scatterer. This is the familiar Doppler shift that leads the field frequency ν and wavenumber k to be changed by the quantities ν D and k D , respectively (Fig. 40.4). Time variations in phase manifest in the beat term exp(−j2πν D t). It should be noted that the effect of displacement, changing index, and Doppler shifting is inseparable. For example, if the sample reflector in Fig. 40.4 were moving as the index was changing, it would be impossible to establish the relative contribution of each term to the phase measurement.
Fig. 40.4
Interferometric phase and scatterer-induced Doppler shift
40.2 Review of Prior Techniques
40.2.1 Monochromatic Interferometric Techniques
Monochromatic phase-sensitive interferometric techniques in cell biology predate their broadband counterparts by approximately half a decade. These monochromatic techniques are not able to perform depth sectioning and effectively integrate phase content along the optical axis. Nonetheless, their ability to measure cell volumes has yielded impressive results.
The maintenance of cell volume and osmolarity are basic homeostatic functions. As such, there is a keen interest in developing techniques that can quantify the response of various epithelial and endothelial cell types to osmotic and/or pharmacologic challenge. Monochromatic interferometry is an attractive candidate for measuring changes in cell volume because the phase of an optical field that is reflected from (or transmitted through) a cell responds linearly to changes in the thickness or optical index of that cell.
This principle was elegantly demonstrated by Farinas and Verkman in 1996 [3]. They performed full-field and single-point monochromatic Mach-Zehnder interferometry in which the reference optical field was mixed with a sample beam transmitted through a single-layer epithelial cell layer (Fig. 40.5). Since the interferometer was monochromatic, this technique is unable to coherently gate phase information at the cell-perfusate interface from that at other interfaces. Farinas and Verkman cleverly circumvented this problem by placing cells in a perfused flow chamber (Fig. 40.5). If it is assumed that the cell acts as a perfect osmometer (i.e., the product of cell volume and cell osmolarity is constant), it then follows that cell expansion (contraction) results from the influx (outflux) of free water into (out of) the cell, leading to a commensurate decrease (increase) in cell osmolarity. Given that the optical index is proportional to osmolarity, and since cell osmolarity is inversely proportional to cell volume per the perfect osmometer assumption, changes in interferometric phase shift are unambiguously related to changes in cell volume. This relationship is qualified with the assumption that the cell thickness scales linearly with cell volume.
Fig. 40.5
Full-field Mach-Zehnder cell volume interferometer (Images are from Farinas and Verkman [3])
The major drawback to this technique was in the retrieval of the interferometric phase data. The setup in Fig. 40.5 is a homodyne detection system insofar as both the reference and sample arm phase velocities are zero. As such, both non-interferometric and interferometric information reside at baseband, precluding the use of various hardware and software time-domain phase-sensitive retrieval techniques. Farinas and Verkman used a nontraditional technique that involved taking the inverse cosine of the data after it was normalized to have values ranging from −1 to +1. Normalization was aided by fringes generated from a spatial phase gradient placed in the reference arm. This inverse cosine operation yields the interferometric phase, but the sensitivity of this technique is limited by the accuracy of the normalization process. As interferometric images were acquired by the use of a CCD camera, imaging speed matched that of the camera frame acquisition rate (∼1 s).
As expected, cells swell in response to a decrease in perfusate tonicity (Fig. 40.5). Since changes in optical index are small compared to the concurrent changes in path length, the change in phase never exceeded 2π. Since zero phase can be defined at the perfusate-coverslip interface, this technique avoids the commonly encountered 2π ambiguity problem that renders phase measurements relative as opposed to absolute.
The approach used by Farinas and Verkman was revisited in 2005 by M. Feld and colleagues [4, 5]. The setup uses a tilted reference arm to generate spatially varying fringes. Two other advances were introduced. First, Hilbert transformation was used to more directly retrieve the complex spatial interferometric signal. Second, a high-speed CCD camera which acquired 480 × 640 pixel images at a 291 Hz frame rate was used. The imaging speed of these systems is compatible with many cell dynamic applications (Fig. 40.6). Nonetheless, the monochromatic sources used prevent depth-selective isolation of the sample behavior.
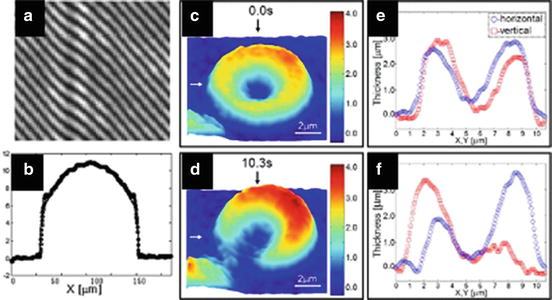
Fig. 40.6
Hilbert phase microscopy applied to static and dynamic objects. Top left: The spatial fringe pattern generated by a tilted reference arm on this image of a bare fiber core has a similar effect to the parallel plates used by Farinas et al. Bottom left: Transverse profile of a fiber core used as a phase object. Rightmost panel of images is the time-varying deformation of a red blood cell recorded using a high-speed version of the technique. (a–b) Are from Ikeda et al. [4] and (c–f) are from Popescu et al. [5]
40.2.2 Broadband Time-Domain Techniques
The use of phase-sensitive detection to extract nonpolarization-based functional information from the interferometric OCT signal was first demonstrated with color Doppler OCT [6, 7]. In CD-OCT, depth-resolved flow information is extracted from the complex-valued signal through a variety of time-frequency analyses. One conceptually straightforward analysis is to calculate the instantaneous Doppler frequency as the derivative of the phase with respect to time. This definition of Doppler shift provides an intuitive understanding of the relationships among phase, Doppler frequency, particle position, and particle velocity. The Doppler frequency (i.e., the derivative of phase with respect to time) is proportional to particle velocity (i.e., derivative of position with respect to time). The phase, which can be viewed as the integral of Doppler frequency, is proportional to the particle position, which is the integral of the particle velocity. Defining phase and position in terms of the integral of Doppler frequency and particle velocity, respectively, has the mathematical convenience of equating the unknown constant of integration with the unknown zero-phase point that generally renders phase, and consequently position, measurements relative as opposed to absolute.
It was in this framework that Yang et al. developed a phase-referenced interferometry (PRI) technique for the measurement of changes in cell diameter in response to an osmotic challenge (Fig. 40.7) [8]. This technique has two advantages over that of Farinas and Verkman [3]. First, because PRI employs a broadband light source, it is able to section via coherence gating signal from interfaces of interest (e.g., cell-perfusate interface) and reject signal from others. Second, since PRI uses a scanning delay line, the interferometric signal was encoded with a characteristic heterodyne beat frequency which allowed for the straightforward extraction of phase by Hilbert transformation of the data. PRI uses a CW source that is harmonically related to the broadband source center wavelength to measure and correct for interferometer jitter introduced by the scanning delay line. This correction was not required in Farinas and Verkman’s full-field setup because data was acquired at a single point in time as opposed to over the course of several seconds. One disadvantage of this setup is that it acquires data pointwise and not in a full-field, parallel manner.
Yang et al. measured the average change in cell thickness of a few cells in response to a moderate hypo- and hypertonic challenge (Fig. 40.7). The reported system sensitivity was 3.6 nm, and the temporal resolution was several hertz. The cells underwent a two-step response to alterations in perfusate tonicity. Upon an increase (decrease) in tonicity, the cells contracted (swelled) for ∼100 s. After this initial response, the cells gradually swelled (contracted) towards a new steady-state thickness.
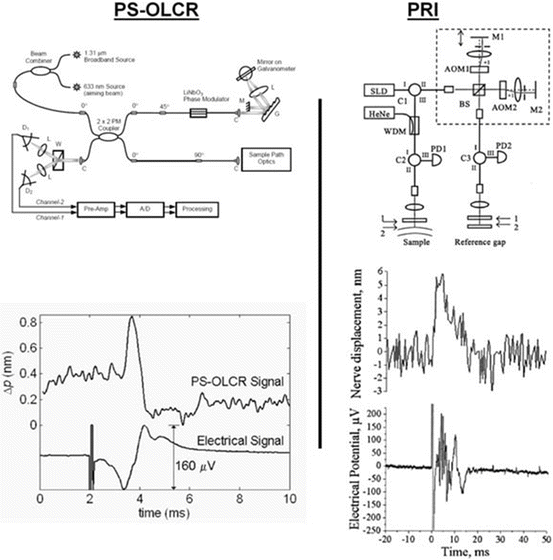
It is a well-established phenomenon that electrical action potentials in a neuron are associated with temporally correlated changes in neuron thickness, birefringence, and optical scattering [9–12]. Fang-Yen et al. [13] employed an improved heterodyne version of the phase-referenced interferometer to visualize such changes in neuron thickness. Rather than using a continuous-wave reference source, this setup employed an additional Michelson interferometer as a phase reference (Fig. 40.8). Phase differences taken between the interrogated sample and a passive reference gap mitigated the effects of phase noise introduced by the added interferometer.
Akkin et al. [14] employed polarization-sensitive optical low-coherence reflectometry (PS-OLCR) to detect action potential-related nerve swelling. The PS-OLCR system (Fig. 40.8) uses two decorrelated polarization channels within a single-mode fiber. Optical path length changes were measured with respect to a selected depth along the optical axis. Longitudinal separation of orthogonal polarization components was achieved by placement of birefringent wedges in path of the sample illuminating light. In the detection arm, the optical phase associated with each polarization was separately detected and determined with the Hilbert transform. The differential phase mitigated common mode noise and provided the relative phase, and therefore path length, change between the two spatially separated polarization channels. Results obtained for electrical stimulation of a crayfish nerve bundle demonstrate subnanometer resolution capabilities of this system (Fig. 40.8).
40.3 Theoretical Limits to Phase Stability in Interferometry
OCT was first demonstrated by Huang et al. in 1991 [15]. Two key insights from this first demonstration were (1) the use of time-domain (TD) low-coherence interferometry techniques developed in telecommunications [16] to obtain depth-reflectivity profiles in biological tissue and (2) the use of laterally scanning sample arm optics to generate two-dimensional optical reflectivity profiles of tissue. It was quickly realized that phase-based information could be extracted from the interferometric OCT signal [6, 7, 17] and that this information could be used to characterize biological tissue.
There are two types of phase information which have been extracted from interferometric OCT signals. The first type is polarization-based phase, which describes the differential propagation of orthogonal polarization states in biological tissue. This technique is not the focus of this chapter and is discussed extensively elsewhere in this book. The second type of phase information is discussed in Sect. 40.1.1 and is referred to here as interferometric phase. This interferometric phase is sensitive to sample motion, Doppler shift, and changes in optical index. For example, in TDOCT, in the absence of sample arm motion and interferometer jitter, the real interferometric phase is proportional to cos(2ko[xR−xS]), where ko is the source center wavenumber, xR is the linearly swept reference arm path length, and xS is the location of a sample reflector of interest. In the setting of sample motion δx, the signal is proportional to cos(2ko[Δx–xo + δx]). If the interferometric phase is measured over successive scans, the relative (but not absolute) position of a reflector can be tracked.
In the early 2000s, it was demonstrated that spectral domain OCT techniques have a substantial amplitude sensitivity advantage over their time-domain techniques [18–20]. This prompted a shift in technology development for amplitude and phase imaging using OCT. With respect to phase imaging, the interferometric phase information is available in the native spectral domain (spectrally but not spatially resolved) or in the time domain (spatially but not spectrally resolved). Data processing to obtain displacement and Doppler data is substantially similar for both TD and SD-OCT. From a practical perspective, SD-OCT holds an advantage over TD-OCT in measuring interferometric phase since SD-OCT systems employ few, if any, moving parts. Additionally, in SD-OCT a common path or coaxial interferometer topology can be employed [21, 22]. This approach has the advantage of forcing virtually all phase noise to be common mode between the reference and sample optical fields. From a theoretical perspective, the phase stability of SD-OCT holds an intrinsic advantage over TD-OCT. This advantage comes from the fact that phase stability is a straightforward function of amplitude stability. This relationship is explored in this section, in the context of SD-OCT. Experimental results that exploit the phase stability of spectral domain techniques are presented later in the chapter.
40.3.1 Phase and Doppler Sensitivity of Spectral Domain OCT
![$$ i(k)=\frac{1}{2}\rho S(k)\delta k\left[{R}_R+{\displaystyle \sum_n{R}_n+2\sqrt{R_r}}{\displaystyle \sum_n\sqrt{R_n}} \cos \left(2k\left[\varDelta {x}_n+\delta {x}_n\right]\right)\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_41_Chapter_Equ1.gif)
Here, S(k) is the source power spectral density, k is wavenumber (radians per meter), δk is the spectral channel bandwidth, ρ is the detector responsivity, R R is the reference arm reflectivity, and R n is the reflectivity of the nth sample reflector. The quantity Δx n + δx n is the position of the nth reflector. Δx n is an integer multiple of the discrete sampling interval in the x-domain, given by mπ/Δk, where Δk is the total optical bandwidth interrogated and m is any positive or negative integer. δx n accounts for subresolution deviations in reflector position away from mπ/Δk. δx n is an important quantity because it primarily manifests in the phase of i(k). Note that n and m are distinct and separate variables: n indexes discrete reflectors in the sample, while m indexes elements in the one-dimensional x-domain A-scan array.
In swept-source OCT, i(k) is directly measured, whereas in spectrometer- based Fourier domain OCT, i(k) is integrated over the A-scan acquisition time in a charge-coupled device (CCD) or similar charge-accumulation detector. In either case, after Fourier transformation of the k-domain signal, the complex-valued x-domain signal and shot noise is given by, respectively,
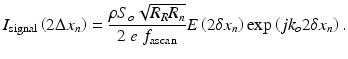
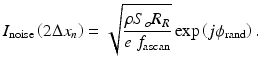
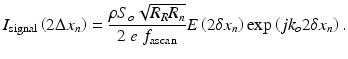
(40.2)
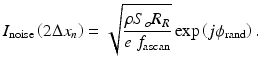
(40.3)
Here, E(·) is the unity-amplitude x-domain autocorrelation function, So is the total sample illumination power (i.e., ∫ S(k)dk), k o is the source center wavenumber, and ϕ rand is the random phase of the shot noise. f ascan is the rate, in Hz, at which A-scans were acquired. In situations where the detector integration time is less than the interval between acquired A-scans, f ascan is the numerical inverse of the integration time. It is assumed that R R >> R n . The amplitude signal-to-noise ratio of the nth reflector is given by the square of the ratio of the amplitudes of Eqs. 40.2 and 40.3. The shot noise-limited phase stability of the nth reflector signal is limited by the phase angle δϕ sens between I signal(2Δx n ) and I(2Δx n ) = I signal(2Δx n ) + I noise(2Δx n ). The issue can be generally approached by considering the average value of the phase angle between I signal(2Δx n ) and I(2Δx n ) over all values of ϕ rand. This is given by (Fig. 40.9)
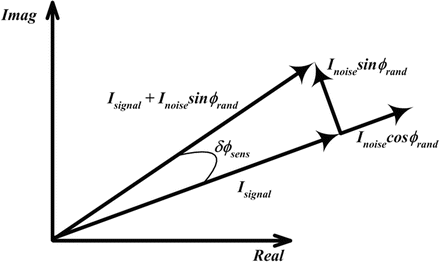
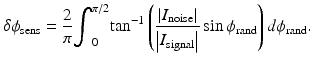
Fig. 40.9
Phase stability of spectral domain phase microscopy. In the x-domain, the signal and noise are complex-valued signals that add in a vectoral manner. If the phase of the noise is defined to be zero when I noise is parallel to I signal, then the error in the phase of I signal is given by the component of I noise that is perpendicular to I signal (i.e., I noise sin ϕrand). The average rotation of I signal caused by I noise sin ϕrand taken over all ϕ rand defines the phase stability
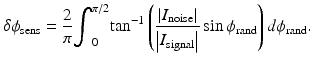
(40.4)
Equation 40.4 is derived in part from the representation of signal and noise in Fig. 40.9. At any particular instant, the signal vector (I signal) and the noise vector (I noise) have a random angular orientation with respect to each other. Since the phase of Isignal is not random, the phase of I noise (i.e. ϕ rand) can be conveniently defined with respect to I signal. I noise can be decomposed into components that are parallel (I noisecosϕ rand) and orthogonal (I noisesinϕ rand) to the signal vector. The parallel component contributes to amplitude sensitivity, while the orthogonal component contributes to the phase sensitivity. The phase noise of I signal is defined by the magnitude of the rotation of I signal by I noisesinϕ rand. The phase noise also defines the phase sensitivity (δϕ sens) since the smallest observable change in the phase of the signal vector is determined by the phase noise. In other words, an observable change in the signal phase must be larger than the phase noise. If ∣I noise∣≪∣I signal∣, which is the usual case, then I signal, I noisesinϕ rand, and I signal + I noisesinφ rand form a right triangle, and δϕ sens is the angle opposite I noisesinϕ rand. δϕ sens is defined by the argument of the integral in Eq. 40.4, while the integral itself takes the average value of δϕ sens over all possible random values of ϕ rand. This integral assumes that ϕ rand has a uniform distribution. If it is assumed that ∣I noise∣≪∣I signal∣, then the arctangent function can be approximated by the value of its argument. The integral in Eq. 40.4 then simplifies to the mean value of the sine function over a quarter period, yielding
