Fig. 9.1
Resolution limits of OCT. OCT can achieve high-axial resolutions independent of numerical aperture. Using low-coherence interferometry, the axial resolution is inversely proportional to the bandwidth of the light source. The transverse resolution is given by the focus spot size. The depth of field is determined by the confocal parameter of the focused beam
As in conventional microscopy the transverse resolution and the depth of focus are determined by the focused transversal spot size, defined as the 1/e 2 beam waist of a Gaussian beam (cf. Fig. 9.1). Assuming Gaussian rays and only taking into account Gaussian optics, the transverse resolution can be defined by
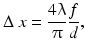
where f is the focal length of the lens and d is the spot size on the objective lens. Increasing the numerical aperture of the objective increases the transverse resolution by reducing the focal spot size, but it decreases the depth of field, quantified by the confocal parameter b, which is 2z R or twice the Rayleigh length 2z R = b = πΔ x 2/2λ. Thus, improving the transverse resolution can be accomplished by increasing the numerical aperture (NA) of the objective, but at the same time decreasing b. A solution to this limitation is the use of a dynamic focus tracking system. Especially for ophthalmic retinal OCT imaging, low numerical aperture focusing is employed, because it is desirable to have a large depth of field and to use OCT to achieve high-axial resolution.
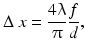
(9.1)
The interference signal detected at the output of the interferometer is the electric field autocorrelation of the light source. As mentioned before, the full width at half maximum (FWHM) of this autocorrelation is the coherence length l c , which gives the axial resolution Δz and is inversely proportional to the width of the power spectrum. The envelope of this field autocorrelation is equivalent to the Fourier transform of the power spectrum. For a source with a Gaussian spectral distribution, the axial resolution Δz is primarily determined by the coherence length of the optical light source given by
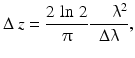
where λ is the center wavelength of the source and Δλ the spectral bandwidth (cf. Fig. 9.1) [12]. Hence, high-axial resolution may be achieved even with low numerical aperture (NA) beam delivery optics. Since the coherence length of a light source is inversely proportional to its spectral bandwidth, broad-bandwidth optical sources are required to improve the axial resolution in OCT, which are important to detect early changes of various diseases occurring at cellular level. To improve axial OCT resolution, the spectral bandwidth must be either increased or the center wavelength decreased. Therefore, novel light sources are necessary – ultrabroad bandwidth solid state lasers have the advantage of providing broad bandwidths necessary for high resolution as well as high power [13]. Since the wavelength in material with a higher refractive index becomes shorter, the actual axial resolution within the imaged tissue can be estimated by dividing the free space resolution by the group refractive index, i.e., 1.35–1.4 for most of the biological tissue. Nevertheless, the axial resolution is also limited not only by the dispersion of the sample but also by absorption and scattering within the sample, where photons with the same path, but backreflected from various imaging depths, are detected.
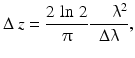
(9.2)
Improving the axial resolution in OCT is challenging and requires the use of highly sophisticated ultrabroad bandwidth light sources. Figure 9.2 depicts “iso-resolution lines,” i.e., the optical bandwidth (at full-width-at-half-maximum (FWHM)) for a given central wavelength necessary to achieve a desired axial OCT resolution. The iso-resolution lines range from 16 to 0.125 μm, measured in free space. For the standard wavelength region used for OCT retinal imaging (800 nm), assuming a Gaussian spectrum of the light source as well as nondispersive imaging medium, this figure shows that for 1 μm axial resolution, an optical bandwidth of ∼200 nm is needed. It also illustrates that in order to achieve the same axial resolution at 1,300 nm, more than 500 nm of optical bandwidth (FWHM) is needed, i.e., more than two times more, compared to what is needed at 800 nm. Finally, in the visible wavelength region (500 nm), only 75 nm is need to achieve 1 μm axial OCT resolution. This demonstrates the significant wavelength dependence and the challenge to balance resolution versus penetration/contrast depending on the particular OCT application.
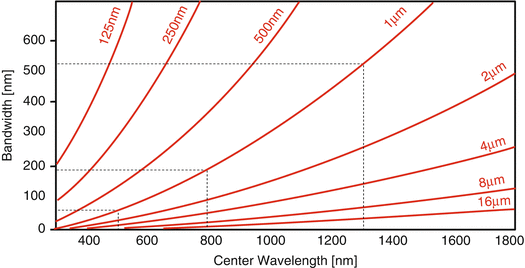

Fig. 9.2
Axial OCT resolution. “Iso-resolution lines” for certain axial OCT resolutions (ranging from 16 to 0.125 μm) indicating necessary optical bandwidth as a function of central wavelength. Significantly broader optical bandwidth is needed for the same axial OCT resolution with increasing central wavelength (cf. dashed lines for 500 nm, 800 nm, and 1,300 nm, respectively)
9.2 Axial Resolution Limits for OCT
9.2.1 Group Velocity Dispersion Limitations to Resolution
Group velocity dispersion (GVD) causes different frequencies to propagate with nonlinearly related phase velocities. A short pulse in dispersive media will broaden if significant dispersion is present. In analogy to the case for short pulses, the interferometric autocorrelation (i.e., the axial PSF) will also broaden if there is GVD mismatch between reference and sample arms. Both the fiber optics and the sample may introduce a significant amount of GVD. To include GVD in the analysis, the propagation constants β R and β S used in the propagation equation are Taylor expanded to second order around the central frequency ω 0.
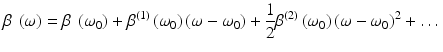
where a GVD mismatch is assumed in a length L of the sample and reference paths. The frequency-dependent phase mismatch
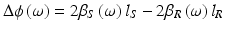
is
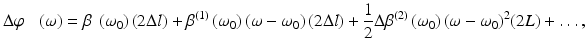
where Δl is defined as the additional geometric path difference and Δβ″ = β″ S (ω 0) − β″ R (ω 0) is the GVD mismatch between the reference and sample paths. Note that only the difference in GVD between the two interferometer arms enters Eq. 9.5. Thus, the deleterious effects of dispersion may be decreased by equalizing the GVD in the two interferometer arms. Inserting Δϕ(ω) into the propagation equation gives the photocurrent
![$$ \begin{array}{l}I\propto \left\{ \exp \left[-j{\omega}_0\Delta {\tau}_{\mathrm{P}}\right]{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}S\left(\omega -{\omega}_0\right) \exp \left[-j\frac{1}{2}\Delta \beta^{{\prime\prime}}\left({\omega}_0\right)\left(\omega -{\omega}_0\right)(2L)\right]}\right.\\ {}\kern0.5em \left.\kern3.5em \times \exp \left[-j\left(\omega -{\omega}_0\right)\Delta {\tau}_{\mathrm{g}}\right]\frac{d\left(\omega -{\omega}_0\right)}{2\pi}\right\},\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_10_Chapter_Equ6.gif)
where Δτ P is the phase delay mismatch and Δτ g is the group delay mismatch. The GVD mismatch multiplies the source power spectral density S(ω − ω 0) in a frequency dependent, quadratic phase term. The interferometric signal looks like a short pulse, with its Fourier transform being S(ω − ω 0), which propagates through a length L of dispersive medium with second-order dispersion equal to the difference in GVD between the interferometer arms. Thus, just as a short pulse broadens and chirps after propagation through a dispersive medium, the interferometric signal should also broaden and chirp due to GVD mismatch in the two interferometer arms.
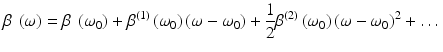
(9.3)
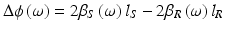
(9.4)
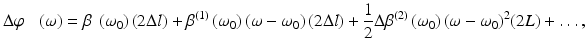
(9.5)
![$$ \begin{array}{l}I\propto \left\{ \exp \left[-j{\omega}_0\Delta {\tau}_{\mathrm{P}}\right]{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}S\left(\omega -{\omega}_0\right) \exp \left[-j\frac{1}{2}\Delta \beta^{{\prime\prime}}\left({\omega}_0\right)\left(\omega -{\omega}_0\right)(2L)\right]}\right.\\ {}\kern0.5em \left.\kern3.5em \times \exp \left[-j\left(\omega -{\omega}_0\right)\Delta {\tau}_{\mathrm{g}}\right]\frac{d\left(\omega -{\omega}_0\right)}{2\pi}\right\},\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_10_Chapter_Equ6.gif)
(9.6)
To establish the analogy further, we assume that the source has a Gaussian power spectral density distribution and after substitution into Eq. 9.6 a modulated interferometric signal with a complex Gaussian envelope is obtained
![$$ I\propto \frac{\sigma_{\tau }}{\Gamma (2L)} \exp \left[-\frac{\Delta {\tau}_{\mathrm{g}}}{2\Gamma {(2L)}^2}\right] \exp \left[-j{\omega}_0\Delta {\tau}_{\mathrm{p}}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_10_Chapter_Equ7.gif)
where σ τ is the single-sided standard deviation. The characteristic width of the axial point spread function in the presence of dispersion Γ(2L) is a complex parameter that depends on both the round trip length of GVD mismatch 2L and σ τ via
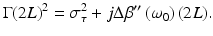
![$$ I\propto \frac{\sigma_{\tau }}{\Gamma (2L)} \exp \left[-\frac{\Delta {\tau}_{\mathrm{g}}}{2\Gamma {(2L)}^2}\right] \exp \left[-j{\omega}_0\Delta {\tau}_{\mathrm{p}}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_10_Chapter_Equ7.gif)
(9.7)
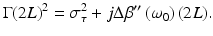
(9.8)
The real and imaginary components of 1/Γ(2L)2 describe the broadening and chirping, respectively, of the interferometric signal and are
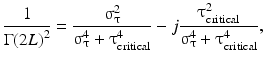
where we have defined the dispersion parameter
![$$ {\tau}_{\mathrm{critical}}={\left[\Delta {\beta}^{{\prime\prime}}\left({\omega}_0\right)(2L)\right]}^{\frac{1}{2}}. $$](/wp-content/uploads/2017/03/A76297_2_En_10_Chapter_Equ10.gif)
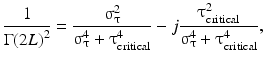
(9.9)
![$$ {\tau}_{\mathrm{critical}}={\left[\Delta {\beta}^{{\prime\prime}}\left({\omega}_0\right)(2L)\right]}^{\frac{1}{2}}. $$](/wp-content/uploads/2017/03/A76297_2_En_10_Chapter_Equ10.gif)
(9.10)
Substituting the expression for 1/Γ(2L)2 into Eq. 9.7, we discover that the Gaussian envelope is broadened to the new standard deviation width
![$$ 2{\tilde{\sigma}}_{\tau }=2{\sigma}_{\tau }{\left[1+{\left(\frac{\tau_{\mathrm{critical}}}{\sigma_{\tau }}\right)}^4\right]}^{\frac{1}{2}}. $$](/wp-content/uploads/2017/03/A76297_2_En_10_Chapter_Equ11.gif)
![$$ 2{\tilde{\sigma}}_{\tau }=2{\sigma}_{\tau }{\left[1+{\left(\frac{\tau_{\mathrm{critical}}}{\sigma_{\tau }}\right)}^4\right]}^{\frac{1}{2}}. $$](/wp-content/uploads/2017/03/A76297_2_En_10_Chapter_Equ11.gif)
(9.11)
The broadening factor becomes appreciable when the magnitude of the dispersion parameter τ critical becomes greater than the non-broadened temporal standard deviation σ τ . For a typical fused silica fiber at 800 nm, 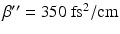 . For a standard resolution achieved by OCT, Δl = 10 μm, implying σ τ = 28 fs. Thus, dispersive broadening becomes a factor if the fiber arm lengths are mismatched by at least 1 mm.
. For a standard resolution achieved by OCT, Δl = 10 μm, implying σ τ = 28 fs. Thus, dispersive broadening becomes a factor if the fiber arm lengths are mismatched by at least 1 mm.
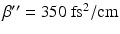 . For a standard resolution achieved by OCT, Δl = 10 μm, implying σ τ = 28 fs. Thus, dispersive broadening becomes a factor if the fiber arm lengths are mismatched by at least 1 mm.
. For a standard resolution achieved by OCT, Δl = 10 μm, implying σ τ = 28 fs. Thus, dispersive broadening becomes a factor if the fiber arm lengths are mismatched by at least 1 mm.The chirping of the interferometric signal with increasing path length mismatch Δl can be described by differentiating the phase in the exponent of Eq. 9.7, leading to
![$$ k=\frac{d\phi }{d\Delta l}=2\beta \left({\omega}_0\right)-\frac{\tau_{\mathrm{critical}}^2}{\sigma_{\tau}^4+{\tau}_{\mathrm{critical}}^4}\left[4\Delta \beta^{{\prime\prime} }{\left({\omega}_0\right)}^2\right]\Delta l, $$](/wp-content/uploads/2017/03/A76297_2_En_10_Chapter_Equ12.gif)
where k describes the spatial frequency of the interference fringes versus the distance measured Δl. For example, in the positive dispersion mismatch regime Δβ″(ω 0) > 0, when the reference arm path length is increased, Δl decreases, the wavenumber k increases, and the interference fringes occur at the detector more often. It is important to note that GVD changes the phase but not the bandwidth of the interference signal.
![$$ k=\frac{d\phi }{d\Delta l}=2\beta \left({\omega}_0\right)-\frac{\tau_{\mathrm{critical}}^2}{\sigma_{\tau}^4+{\tau}_{\mathrm{critical}}^4}\left[4\Delta \beta^{{\prime\prime} }{\left({\omega}_0\right)}^2\right]\Delta l, $$](/wp-content/uploads/2017/03/A76297_2_En_10_Chapter_Equ12.gif)
(9.12)
Dispersion mismatch also degrades the peak height of the interferometric envelope, which reduces the system dynamic range. The degradation in the photocurrent amplitude is described by the multiplicative factor of Eq. 9.7.
![$$ \frac{\sigma_{\tau }}{\left|\Gamma (2L)\right|}=\frac{1}{{\left[1+{\left({\tau}_{\mathrm{critical}}/{\sigma}_{\tau}\right)}^4\right]}^{\frac{1}{4}}}. $$](/wp-content/uploads/2017/03/A76297_2_En_10_Chapter_Equ13.gif)
![$$ \frac{\sigma_{\tau }}{\left|\Gamma (2L)\right|}=\frac{1}{{\left[1+{\left({\tau}_{\mathrm{critical}}/{\sigma}_{\tau}\right)}^4\right]}^{\frac{1}{4}}}. $$](/wp-content/uploads/2017/03/A76297_2_En_10_Chapter_Equ13.gif)
(9.13)
The reduction of the signal amplitude peak scales as the square root of the broadening. Assuming that the dynamic range is measured in terms of reflected optical power, which is proportional to photocurrent power, the loss in dynamic range scales linearly with the broadening.
While first-order dispersion only affects the electromagnetic phase inside the envelope of the signal, leaving the envelope itself unaffected, the second-order frequency dependent refractive index of material introduces a time-dependent change of the instantaneous frequency and an increase of the envelope’s width, which are associated with a loss of signal intensity. Commonly this effect is also called “chirp,” since the acoustic analogue for dispersion is found in the sound that songbird makes. The different frequencies are also shifted in respect to each other, resulting in a high pitched tone that falls for each chirp. The zero-order term of dispersion only introduces a temporal shift of the whole pulse and is equivalent to the refractive index; the higher indices distribute the phase of different frequencies in time and alter the shape of the pulse envelope (cf. Fig. 9.3). Dispersion distributes signal power away from the central peak where all spectral components are in phase to the wings, thereby distorting the envelope of the signal. In case of an originally unchirped pulse with Gaussian envelope second-order dispersion, also called group dispersion delay (GDD) generates symmetric side lobes where parts of the different continuous wave components interfere constructively. Higher-order dispersion, such as third-order dispersion (TOD) or fourth-order dispersion (FOD), introduces satellite pulses, in the form of a pulse train. In contrast to the generation of ultrashort pulses, the dispersion effects in OCT do not involve complete reversion, but can be cancelled (in the case of static dispersion) by balancing the dispersion in both arms of the interferometer. Therefore, the cross-correlation becomes a linear autocorrelation again, which is indistinguishable if the spectral content is constant. Compensation of a lens systems consisting of multiple exotic glass types involves a comparable, complex mixture of dispersion compensation materials.
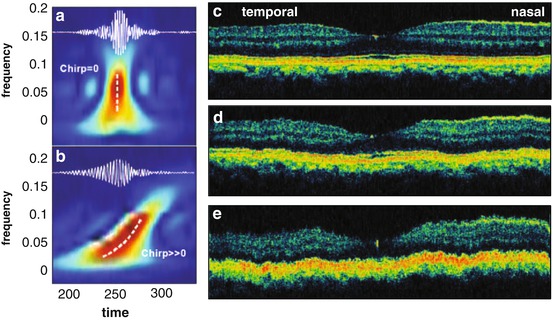

Fig. 9.3
Group velocity dispersion effect on axial resolution in ultrahigh-resolution OCT. Dispersion effect on an actual pulse (a, b); inlet: measured cross-correlation interference pattern and time-frequency diagram of a pulse pair without (a) and with (b) high-order dispersion difference. Frequencies are shifted in time (chirp) and the amplitude is reduced, while the envelope is broadened. Effect of dispersion mismatch in in vivo ultrahigh-resolution retinal imaging (c–e). Dispersion matched (c); artificially introduced dispersion mismatch by 3 mm (d) as well as 9 mm (e) fused silica in the reference arm. Clear axial resolution as well as sensitivity (–5 dB) degradation is observed
In summary, the two arms of an OCT interferometer must have almost the same delay as well as similar second- and higher-order dispersion (GDD, TOD). The first-order dispersion, however, does not play a role for the interference envelope and therefore is irrelevant for measuring the position. However, FOD does affect the phase and changes the readings for complex analysis of material properties (see in the following chapters). For ultrahigh-resolution retinal OCT imaging, the dispersion of approximately 25 mm ocular media can be compensated by using 25 mm of water in the reference arm, since previous in vivo studies of dispersion measurements have shown that the dispersion of ocular media averaged over 25 mm is similar to the that of 25 mm of water [14]. Balancing the higher-order contributions to dispersion of the 25 mm ocular media in front of the retina is more critical for obtaining high resolution than balancing the dispersion of the system itself. Figure 9.3 depicts the effect of dispersion mismatch in the case of in vivo ultrahigh-resolution retinal imaging of a normal human fovea (cf. Fig. 9.3c). By artificially introducing dispersion mismatch by inserting 3 mm (cf. Fig. 9.3d) and 9 mm (cf. Fig. 9.3e) fused silica in the reference arm of the OCT interferometer, it is obvious that both OCT resolution and sensitivity (up to –5 dB) decrease. Clinical studies with ultrahigh-resolution ophthalmic OCT utilizing ∼100 nm broad spectra revealed that by using a dispersion compensation of 25 mm of water in the reference arm of the interferometer, patients with axial eye lengths between 23 mm and about 27 mm can be imaged with tolerable dispersion mismatch-induced axial resolution loss. Furthermore, numeric compensation can be used for further enhancement and fine tuning of the physical compensation, but not as a replacement. This is the result of the inevitable detection and amplification noise in the original signal. In case the signal is so strongly dispersed, that it is below the noise level, the signal is completely corrupted by noise and cannot be recovered numerically. Therefore, it is favorable to physically compensate static dispersion mismatch.
9.2.2 Dispersion and Resolution in FD OCT
The interference signal in spectrometer-based frequency-domain OCT can be recorded as a function of wavelength rather than time. In case of a single reflecting surface in the sample arm, it is of the general form
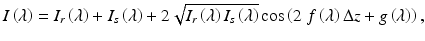
where I r and I s are the intensity of the reference and sample arm light, respectively, and Δz is the relative optical path length between both arms. The functions f(λ) and g(λ) are crucial, since they determine the resolution of the OCT system. In general one needs to Fourier transform the backscattered intensity as a function of wavenumber k or frequency ν in order to reconstruct the associate time-domain depth profile. Ideally g(λ) is only an arbitrary phase constant that can be neglected without loss of generality, and f(λ) = K = 2π/λ. Assuming, however, a dispersion mismatch between both arms associated with a material thickness d, g(λ) will no longer be constant but of the form g(λ) = 2d/f(λ)(n(λ) −1), where n(λ) is the wavelength-dependent refractive index of the dispersive material. It is well known that the dispersion dn(λ)/dλ and higher-order terms cause a broadening of the envelope of the time-domain signal; therefore, the dispersion mismatch between reference and sample arm needs to be minimized to achieve optimal depth resolution. Especially in the case of retinal imaging, one also needs to compensate for the dispersive ocular media that the light double passes on its way to the retina and back to the detector [15].
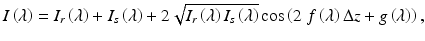
(9.14)
In order to minimize g(λ) one needs to balance the dispersion mismatch between both interferometer arms. Once g(λ) has been optimized, we are still left with f(λ) which describes a nonlinear phase as a function of wavelength λ in the cosine term of Eq. 9.14. This nonlinearity causes an additional broadening of the coherence envelope after discrete Fourier transform (DFT) of Eq. 9.14. Apart from the relation λ ↔ K, it is due to dispersion of the diffraction grating, imaging errors of the optical system in front of the CCD, misalignment, finite CCD pixel sizes, or surface imperfections of the optics. The actual nonlinear phase function needs to be resampled to provide equally spaced interference fringes. There is a residual nonlinearity due to the factors that have been mentioned previously which causes a broader coherence envelope as compared to that obtained with the resampling technique. It is obvious that a small nonlinearity already causes a significant decrease of depth resolution. Further resolution and sensitivity loss occurs as a result of the finite pixel width of the spectrometer together with the limited dynamics of the individual pixel. Due to the recorded chirped interference pattern, there will be always higher frequencies at one end of the modulated spectrum which appear with a reduced modulation depth, as will be explained in the next section. Hence, the effective spectral width of the FD OCT signal is reduced, which results in a resolution loss for structures which are closer to the maximal depth position.
9.2.3 Spectral Shape of Ultrabroad Bandwidth Light Sources
Light sources for UHR OCT not only require high spatial coherence and ultrabroad bandwidth emission with enough output power and low noise but should also have an optimal spectral shape. Since the coherence length is defined as the full width at half maximum of the field autocorrelation measured by the OCT interferometer, the width and also the shape of the coherence function of an OCT system depend on the spectral shape of the light source as well as on the transfer function of the OCT system. The transfer function is mainly determined by the optical properties of the interferometer, as described in detail later. The ideal spectrum for OCT would have Gaussian spectral shape, resulting in a Gaussian coherence function with no side lobes. Large spectral modulations would reduce sensitivity and resolution, due to the presence of side lobes in the fringe pattern that appear symmetrically to the coherence-function maximum. There are several approaches to change the shape of the emission spectrum of the light source. The easiest way is to introduce optical dichroic or interference filters that suppress certain wavelength regions. Another possibility, especially for very wide spectra, is to spatially disperse the optical beam with prisms and to induce local and therefore wavelength-dependent losses by filtering the dispersed light beam. Especially for nonlinear laser sources, the temporal stability of the spectral properties, i.e., at the time frame of the single depth measurement is essential to maintaining high resolution. Spectral noise, which cannot be optically filtered, can be reduced numerically during post-processing, but always results in a loss of dynamic range and reduction in the full spectral potential.
9.2.4 Chromatic Aberration Limitations to Resolution
Another limitation for achieving ultrahigh resolution is the chromatic aberration of the optics used in the system. Conventional lenses have a focal length which varies with wavelength and thus focus ultrabroad bandwidth light to different planes. This variation in focal position for different wavelengths alters the local effective bandwidth and therefore degrades resolution. For specially corrected achromatic optics, different imaging distances introduce a wavelength-independent attenuation of the whole spectrum, thereby maintaining the spectral shape, optical bandwidth, and therefore axial resolution. Hence, appropriate achromatic objectives have to be used to maintain the ultrabroad bandwidth of the light in order to achieve ultrahigh resolution. Alternatives are reflective objectives like catadioptrics, consisting of parabolic mirrors that have no chromatic aberration and do not introduce dispersion as found in transmittive elements. For ophthalmic OCT chromatic aberration of the eye itself ultimately limits the axial resolution of ultrahigh-resolution retinal OCT imaging if not properly compensated [16–18].
9.2.5 Other Limitations to Resolution
9.2.5.1 Polarization
Another effect that limits axial OCT resolution in UHR OCT systems is polarization mismatch between the interferometer arms and polarization dispersion (loss of polarization) that introduce a phase difference and therefore a change in the shape of the coherence function and axial resolution, respectively. Polarization changes of the static system can be compensated; however, the loss of a single polarization state and sample birefringence leads to an improper overlapping of the reference and sample light, with severe modulations of the interference spectrum. UHR OCT therefore requires careful polarization control and the polarization dependence of light sources is also an important parameter.
9.2.5.2 Optical Components
The optical transmittance, coating, and wavelength-dependent losses of the bulk or fiber optics, delivery system optics, and also the human eye itself – in case of ultrahigh-resolution ophthalmic OCT – strongly influence the axial resolution as well as the sensitivity of the OCT system. Single-mode and sometimes polarization-maintaining fibers with appropriate cutoff wavelengths should be used to provide light propagation without intra- and inter-fiber interference. Conventional fiber couplers are designed to maintain 3 dB splitting over a narrow wavelength range of typically ± 10 nm. By using these fiber couplers for delivery of broad bandwidth laser light, unequal beam-splitting with respect to wavelength and power can occur and reduce resolution. Hence, special broad bandwidth and wavelength flattened fiber or bulk optic beam splitter have to be used to maintain broad bandwidths and consequently high-axial resolution. Optical circulators are often used in OCT systems in order to design more power efficient and sensitive interferometers, since nonreciprocal elements reduce power delivery losses from the source to the sample and signal losses from the sample to the detector. However, the large optical bandwidths of more than a fourth of an optical octave (e.g., 200 nm bandwidth at 800 nm) require extremely broad band components to avoid impose wavelength-dependent losses.
9.2.5.3 Detection System
Depending on the method of acquiring the interference signal, the detection system, including electronics as well as digitization and acquisition of the interference signal, must avoid degradation of axial OCT resolution. Hence, the transimpedance amplifier used in time-domain and tunable laser-driven FD-OCT systems, and in particular the electronic band pass filtering, must be designed properly and adapted to the ultrabroad optical bandwidth. The electronic bandwidth of the band pass filter must not be too narrow to reduce the axial resolution, but must also not be too broad to reduce sensitivity by introducing noise. Real-time adaptive filtering can help to optimize sensitivity and maintain axial resolution. In time-domain OCT hardware demodulation must be adapted to the scanning speed and optical bandwidth to avoid broadening caused by the time response of the electronics, resulting in a larger coherence length of the envelope as compared to the full interference fringe signal. Finally, the signal must be correctly temporally digitized with at least five to ten times over sampling in respect to the central wavelength, Doppler shift, as well as scanning speed in order to not degrade the achieved axial resolution. With tunable lasers, the linearity of the scan has to be adjusted or alternatively the k-trigger can be used to generate a scan discretely sampled in k-space. Most tunable laser technology, however, usually is limited to standard bandwidths and cannot achieve ultrahigh resolution. To utilize broadband light sources in the frequency domain, the camera technology and the already-mentioned nonlinearities and sampling problems are the factor that can be compensated with sophisticated post-processing techniques.
9.2.5.4 Mechanical Components
Finally the mechanical performance of the scanners used for transverse and/or depth scanning should be accurately selected and correctly controlled. Mechanical jitter or displacement of adjacent depth scans as well as noisy control signals of the scanner might result in distorted and therefore degraded resolution UHR OCT tomograms.
Figure 9.4 summarizes the different factors that limit axial resolution performance in OCT for a time-domain-based ophthalmic UHR OCT system. In this case, the delivery systems as well as the eye itself impose challenges for accomplishing ultrahigh-axial OCT resolution. The limitations indicated are also valid for swept source OCT and Fourier-domain OCT systems. In addition to the limitations mentioned in Figure 9.4, specifications of the tunable light source (e.g., linearity, speed, and linewidth of the sweep across a certain optical bandwidth) for swept source/Fourier-domain OCT as well as specifications of the spectrometer for spectral/Fourier-domain OCT have to be taken into account.
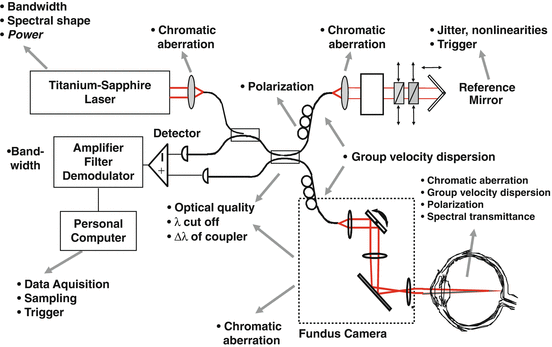

Fig. 9.4
Axial resolution limits in ultrahigh-resolution OCT. Summary of all limitations for a time-domain OCT based system for ophthalmic imaging: light source, spectral transmittance of OCT system, delivery system, spectral properties of sample (in this case the human eye), as well as detection and data acquisition specifications
9.3 Ultrahigh-Resolution OCT at 800 nm
As mentioned above, a significant difference between OCT and conventional microscopy is that OCT achieves very high-axial image resolutions independent of focusing conditions, because the axial and transverse resolution are determined independently by different physical mechanisms. The axial OCT resolution can be enhanced using broad bandwidth, low-coherence length light sources. It is important to note that the light source not only determines axial OCT resolution via its bandwidth and central emission wavelength but also influences both the penetration in the sample (biological tissue) and the OCT transverse resolution. A tissue-specific output power and low noise is necessary to enable high sensitivity and high-speed, real-time, OCT imaging. Hence, it is obvious the light source is the key technology for an OCT system and proper choice is imperative [13].
Historically the longitudinal resolution of OCT systems was limited by the optical bandwidth of the light source. Typically superluminescent diodes with 20–30 nm bandwidth yielded ∼10–15 μm axial resolution. In ophthalmic applications, this provided more detailed structural information than any other standard retinal imaging technique. However, the resolution is significantly below what can be achieved technically and is insufficient to identify individual cells or to assess subcellular structures such as nuclei or mitotic figures. Due to the lack of broad bandwidth, spatially coherent light sources, OCT imaging has been mainly limited to the 800 nm and 1,300 nm wavelength region. Incandescent light sources, although broad bandwidth, produce very little intensity in a single spatial mode. Nevertheless, some research groups have demonstrated these broadband light sources for improving axial imaging resolution by employing a technique that uses a multitude of mutually incoherent low-coherence interferometry channels in order to increase the probe beam power [19] or by using a Linnik-type interference microscope in combination with a CCD camera-based parallel detection scheme [20, 21]. 1 μm isotropic free space axial resolution could be accomplished for in vitro UHR OCT. The first demonstration of sub-10-μm-axial-resolution was achieved by using broadband fluorescence from organic dye [22] and fluorescence from titanium:sapphire [23]. However, biological imaging could not be performed with these light sources due to their low brightness. By multiplexing spectrally displaced superluminescent diodes to increase optical bandwidth [24–26], OCT tomograms with improved ∼7 μm axial resolution in the retina were demonstrated several years ago [27]. More recently, cost-effective, broad bandwidth advanced SLD light sources have become available which approach the image resolutions achieved by femtosecond lasers [28, 29]. These light sources are multiplexed SLDs consisting of two or three spectrally displaced SLDs which are combined to synthesize a broad bandwidth spectrum. Multiplexed SLD light sources have the disadvantage of having spectrally modulated emission spectra that can produce sidelobes in the coherence function or axial point spread function, resulting in image artifacts. In addition, the emission wavelength of multiplexed SLDs is typically centered at the longer 900 nm wavelength range, overlapping the water absorption at 980 nm, which can limit the resolution for retinal imaging. On the positive side, multiplexed SLD light sources are much lower cost and more robust than femtosecond lasers and promise to enable wider availability of ultrahigh-resolution OCT. However, at the present time, the price vs. performance trade-off remains such that UHR OCT instruments with 2–3 μm axial resolution are still limited to research applications. The newest commercial ophthalmic instruments have broad bandwidth, single SLDs and provide 5–8 μm axial image resolution.
Nowadays, ultrashort light pulses can be generated by a range of laser technologies and have widespread applications for ultrafast measurement. Femtosecond laser development has concentrated mainly on the temporal features of the pulses, which were sometimes optimized to the detriment of the spectral shape. In OCT, the pulse shape and duration are irrelevant, while the spectral shape and width play a crucial role. However, unlike ultrafast femtosecond time-resolved measurements where special care must be exercised to maintain the short pulse duration, OCT measurements depend on field correlation, rather than intensity correlation, and every wavelength component interferes independently. Field correlation is preserved even if the pulse duration is long. Femtosecond mode-locked solid state lasers can generate ultrabroad bandwidth, low-coherence light with a single spatial mode and high power, providing both high resolution and high power necessary for high-speed OCT imaging. These lasers can operate over a broad range of wavelengths extending beyond their gain bandwidth by employing nonlinear broadening effects. These spectra are useful for ultrahigh-resolution as well as spectroscopic OCT imaging in tissue. In an early demonstration, a titanium:sapphire laser was used for in vitro OCT imaging in nontransparent tissues with 4 μm axial resolution [30]. In preliminary studies, an OCT system was developed and optimized to support 260 nm of optical bandwidth from a state-of-the-art titanium:sapphire laser [8]. This laser was developed in collaboration with other investigators (Franz Kaertner and Erich Ippen) at M.I.T. and generated pulses of <5.5 fs duration, corresponding to bandwidths of more than 350 nm at 800 nm center wavelength [31]. This high performance was achieved using specially designed double chirped mirrors with high reflectivity bandwidth and controlled dispersion response. Figure 9.5 shows a comparison of the spectra and resolution of an OCT A-scan using a conventional superluminescent diode light source versus the femtosecond titanium:sapphire laser source. The ultrabroad bandwidths which are generated by the femtosecond laser enable the axial resolution of OCT to be improved by a factor of nearly 10× compared to standard OCT technology. This femtosecond laser source was used for imaging studies using an OCT microscope as well as an ophthalmic system interfaced to a biomicroscope system.
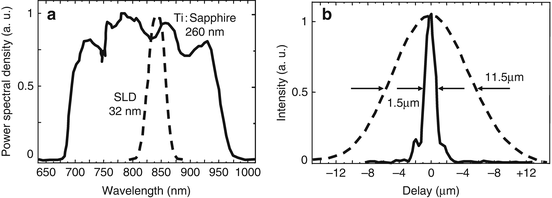

Fig. 9.5
Light source technology for ultrahigh-resolution OCT. Solid state laser light sources enable ultrahigh-resolution imaging. The spectrum of the titanium:sapphire laser versus a standard superluminescent diode (SLD) is shown depicting their respective wavelength bandwidths (a). Demodulated OCT axial scan showing the axial resolution of OCT using titanium:sapphire (solid) versus a superluminescent diode SLD (dashed) light sources (b). Solid state lasers enable almost a 10× improvement in resolution [8]
Figure 9.6a, d show the first in vivo UHR OCT results (presented at SPIE – Photonics West in San Jose, CA in January 1999). The images demonstrate the feasibility of this novel OCT system for in vivo subcellular imaging of a Xenopus laevis (African tadpole, left) mesenchymal cells at 1 × 3 μm (longitudinal × transverse) resolution, consisting of 1,600 × 1,200 pixels and 0.4 × 0.5 μm pixel spacing. Figure 9.7b, c, d show preliminary results demonstrating in vivo ultrahigh-resolution retinal OCT imaging in human subjects [9, 32]. These results were achieved with an ultrahigh OCT system based on a laboratory laser system that was not suited for clinical studies. Therefore, a new generation of compact ultrahigh-resolution OCT system was developed. Femtosecond lasers with record low pump requirements enabled a significant reduction in cost [33]. With advanced mirror technology, dispersion control, and adapted cavity design, optical bandwidth of up to 300 nm at full width of half maximum (FWHM) centered at 790 nm could be achieved resulting in sub-μm axial resolution OCT in tissue. Light sources were optimized with respect to compactness, cost-effectiveness, and applicability in the clinical environment with the aim of realization of a commercially available product for UHR OCT. An integrated and sealed system including a low-cost pump laser on a small footprint of about 500 mm × 180 mm was developed. Due to its compactness, the system shows a high stability and reproducibility and facilitated the technology transfer to a commercial product. With the release of compact, cost-effective, user-friendly state-of-the-art titanium:sapphire laser (Integral OCT), Femtolasers Produktions GmbH has established this novel OCT light source in industry. A compact design as well as active feedback loops guarantees output parameters of unprecedented quality, stability, and reproducibility. In addition, recently reported, cost-effective approaches for broad bandwidth light sources also took advantage of the lower power demand with ultrahigh-resolution OCT imaging [33–37].

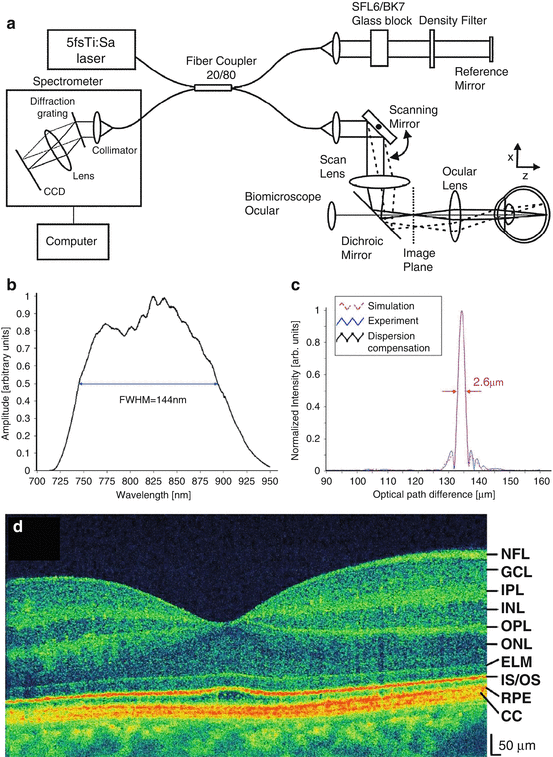

Fig. 9.6
First in vivo ultrahigh-resolution OCT. In vivo subcellular resolution OCT (a, d) in a developmental biology animal model (African tadpole). Standard resolution OCT (performed with the second generation commercial OCT system – OCT II; b) versus ultrahigh-resolution ophthalmic OCT (c–e) of the living human retina. Preliminary results presented in 1999 at SPIE Photonics West (a–c); improved results published in [8, 9] (d, e)

Fig. 9.7
High-speed, ultrahigh-resolution OCT imaging of the human retina. A spectral/Fourier-domain OCT system (a) using a 5 fs laser was used to demonstrate high-speed, ultrahigh-resolution imaging with an axial line rate of 16,000 lines/s. Source bandwidth (b) measured ∼144 nm, which provided resolution of ∼2.1 um in tissue (c). The system enabled high-definition, motion-free imaging of the human retina (d)
Ophthalmic UHR OCT using these state-of-the-art light sources achieves superior axial image resolutions of 2–3 μm as compared to ∼10 μm resolution in standard OCT, enabling the visualization of intraretinal structure. UHR OCT is a key step toward achieving noninvasive optical biopsy of the human retina, i.e., visualization of intraretinal morphology in retinal pathologies approaching the level achieved with histopathology. UHR OCT technology has been investigated in clinical settings to assess its clinical utility. Cross-sectional studies in ∼1,000 eyes with different pathologies demonstrated unprecedented visualization of all major intraretinal layers and provided especially significant information about the photoreceptor layer [10, 38–46]. These studies demonstrated visualization of photoreceptor layer impairment in macular pathologies such as macular holes, central serous chorioretinopathy, age-related macular degeneration, foveomacular dystrophies, Stargardt’s dystrophy, and retinitis pigmentosa (cf. also Chap. 34, “MUW Approach of PS OCT”).
More recently, high-speed and three-dimensional techniques have been developed for ultrahigh-resolution ophthalmic OCT. Spectral/Fourier-domain OCT methods make use of a spectrometer and a line scan camera to acquire all depths of the OCT axial scan simultaneously in the frequency domain [47, 48]. Fourier-domain OCT can also be performed using the swept source method, whereby a narrowband laser source is scanned in wavelength over a broad bandwidth and the frequency encoded OCT axial scan is acquired as a function of time with a balanced photoreceiver [49]. In either case, the signal is reconstructed using a Fourier transform. The Fourier-domain approaches are performed without the need for moving part scanners in the reference arm and are therefore scalable to much higher speeds than traditional time-domain OCT scanners. High-speed imaging is further facilitated by the fact that spectral and swept source OCT leads to a sensitivity advantage compared to time-domain OCT that scales with the number of points in the acquired data set and is typically in the range of 20–30 dB improvement [50–52]. High-speed ophthalmic OCT was first demonstrated with standard resolution using the spectral domain approach at 800 nm [47, 48]. Subsequent work then demonstrated high-speed, ultrahigh-resolution OCT [53–55]. Figure 9.7 presents results from a high-speed, ultrahigh-resolution OCT system using a 5 fs Ti: Sapphire laser source [53]. The system schematic in Fig. 9.7a illustrates the spectrometer detection system and the static reference arm. The broadband spectrum measuring ∼144 nm FWHM is shown in Fig. 9.7b. This resulted in an axial resolution of 2.1 um in tissue, shown in Fig. 9.7c. The high-phase stability of Fourier OCT systems facilitates numerical processing techniques there were previously difficult with time-domain OCT, such as numerical dispersion compensation. A representative image of the human macula is shown in Fig. 9.7d. High-speed acquisition of ultrahigh-resolution scans enables motion-free, high-definition images.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


