, Anne Latrive2, 1 and A. Claude Boccara1, 3, 4
(1)
LLTech SAS Pépinière Paris Santé Cochin, 27 rue du Faubourg Saint Jacques, Paris, 75014, France
(2)
Institut Langevin, ESPCI ParisTech, Paris, France
(3)
LLTech, Princeton, NJ, USA
(4)
Institut Langevin, ESPCI–ParisTech, Paris, France
Keywords
Full field OCTFull Field OCMSignal to noise ratioEndoscopy25.1 Signal Introduction: OCT Acquisition and Multiplexing
For time- or frequency-encoded OCT systems samples, sections are obtained by quickly acquiring voxels along the optical axis of the imaging system [1–5]. More precisely the data is acquired along cylindrical sections of the samples that have roughly the length of the depth of field and then by scanning the beam along the sample surface. Differently, full-field OCM (FFOCM) [6–9] produces “en face” images (i.e., of a plane layer parallel to the sample surface) without scanning the light beam. FFOCM detects the interferometric signal across a plane section of the sample at a given depth and a 2D slice is thus obtained directly. When using this geometry, we can understand the main advantage of FFOCM over the competing OCT approaches: it allows the use of medium to large numerical aperture microscope objectives with a high transverse resolution of about one micrometer. For this reason in our first paper, we called it full-field optical microscopy (FFOCM) [10] and other authors did the same later [11], so we will continue here to use FFOCM because the microscopic resolution is more and more required for the various applications of this technique.
To record these images, the entire field is illuminated by a spatially incoherent source with low temporal coherence length (i.e., broadband) and is acquired on megapixel detectors such as CCD or CMOS cameras. The difference between FFOCM and OCM (see Chap. 26, “Assessment of Breast, Brain and Skin Pathological Tissue Using Full Field OCM” about OCM) is that OCM takes also “en face” images but uses a single spatial mode optical source (laser or SLD) that is focused by a microscope objective and scanned at the required depth [12, 13].
In the time-domain OCT approach, each voxel of the sample volume is scanned sequentially; a significant improvement has been achieved using spectroscopic or Fourier domain OCT that multiplexes the data by acquiring in parallel all the voxels along a line: typically a few hundred voxels are simultaneously acquired using a fast linear detector working in the kHz range. Typical values are of the order of megavoxels/s.
FFOCM allows millions of voxels acquisition in a few tens to thousand images/s range depending of the camera speed and the required signal-to-noise ratio. Here typical values are in the range of 100 megavoxels/s.
25.2 Full-Field Optical Coherence Microscopy
25.2.1 FFOCM: The Experimental Setup
In the case of full-field optical coherence microscopy, we combine an interferometer and a microscope. The experimental setup is shown schematically in Fig. 25.1. This is a Michelson interferometer in the Linnik configuration where two identical microscope objectives are used in the object arm and in the reference arm.
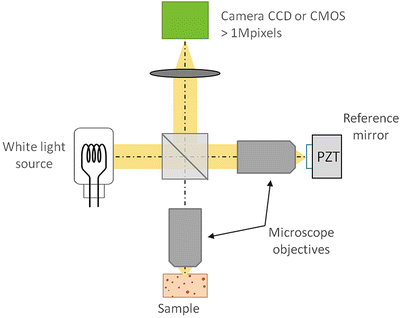
Fig. 25.1
Principle of the full-field OCM setup
Here we will describe the basic principles of the setup and the elementary signal processing.
The light source chosen for our system is a simple halogen lamp tungsten filament with a nominal power of 150 W that illuminates the interferometer via a Koehler illumination device that allows obtaining a homogeneous illumination of the sample. The emission spectrum of the source is very broad and can be modeled by that of a black body centered in the near infrared around 800 nm. This broadband incoherent source has a very short spatial and temporal coherence length leading to a sub-micrometer sectioning ability and avoiding cross talk.
The light beam emitted by the source is divided into the two arms of the interferometer through a broadband non-polarizing beamsplitter cube. The average power impinging the sample is of the order of 1 mW/mm2.
The objectives that are mostly used for biomedical applications are immersion ones (oil or water) in order to reduce the surface reflection and to minimize the aberrations induced by the surface topographic irregularities. Routinely 10× water immersion objectives with a 0.3 numerical aperture (NA) are used but we have also used 20× (0.5 NA, water), 40× (0.8 NA, water), and 30× (1.05 NA, silicone oil) and a few more objectives working in air. The choice of two identical microscope objectives minimizes the path differences between the two arms and maximizes the overlap between the interfering wavefronts. The use of a sample immersion liquid (mostly buffer solutions) increases the duration of biological samples observation without damaging them under illumination.
Furthermore, using liquid immersion microscope objectives minimizes chromatic dispersion between the two arms when images are formed in depth.
25.2.1.1 Image Acquisition
The tomographic image intends to reveal the intensity reflected by a slice at a chosen depth; we call it R obj (x, y). The backscattered amplitude is calculated using the combination of two or four images obtained for two or for values of the phase ψ shifted by π or π/2, respectively. The recorded signal is given by
![$$ I\left(x,y,t\right)=\frac{I_0}{4}\left\{{R}_{inc}\left(x,y\right)+{R}_{ref}\left(x,y\right)+2\sqrt{R_{obj}\left(x,y\right){R}_{ref}\left(x,y\right)} \cos \left[\phi \left(x,y\right)+\psi \right]\right\} $$](/wp-content/uploads/2017/03/A76297_2_En_26_Chapter_Equa.gif)
where ϕ is the (unknown) phase difference between the reference signal and the object signal of the signal, ψ is the phase shift induced by the shift of the reference mirror, I 0 is the photon flux at the entrance of the interferometer, R ref is the (rather uniform) reference mirror reflectivity, R obj (x, y) is the fraction of light reflected by the object that interferes with the reference beam, and R inc (x, y) is the fraction of light that does not interfere (light backscattered by the other slices of the sample, and the stray light of the interferometer). More precisely R obj (x, y) represents the reflectivity distribution of the sample structures contained in the coherence volume. R obj (x, y) thus corresponds to an en face tomographic image.
The two possible choices of two or four images need to be clarified:
One can see easily that if R ref is uniform over the field of view, four successive values of ψ (e.g., 0, π/2, π, 3π/2) allow to isolate the term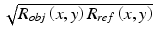
that is proportional to 
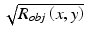that is the amplitude of the backscattered signal intensity.
OCT images always contain speckle because of the interference of the light backscattered by different tissue microstructures located inside the coherence volume. For this reason the amplitude and the phase of the recorded backscattered signals are random and we do not lose too much information by simply taking two images (instead of four) and rely on the absolute value of the real part of the complex signal (instead of the amplitude).
A software was developed to calculate and display the tomographic image in real time (at several tens of Hertz, depending on the camera frame rate and the computer speed).
By moving the sample step by step in the axial direction, one may acquire a stack of en face tomographic images. Once a three-dimensional data set is recorded, sections of arbitrary orientation can be extracted. Volume-rendering images can also be computed.
25.2.1.2 Full-Field OCM: Spatial Resolution and Sensitivity
As we mentioned earlier since conventional OCT produces axially oriented images, a depth of field equal to the axial extent of the images is required to avoid dynamic focusing as the coherence gate is scanned. Low-NA lenses are then used in order to obtain a large depth of field, which consequently limits the transverse resolution.
Full-field OCM produces en face tomographic images. In this configuration, microscope objectives with relatively high numerical aperture (NA) can be used. The transverse resolution of full-field OCM is that of a microscope, i.e., of the order of 1 μm.
Nevertheless as conventional OCT, full-field OCM has an axial resolution determined by the coherence length of the illumination source. In contrast to the spectrum of ultrashort femtosecond lasers, the spectrum of a thermal light source is very smooth. It does not contain spikes or emission lines that could cause side lobes in the coherence function and create artifacts in the images. In addition, the optical power is much more stable. The effective spectrum of the system is actually imposed above all by the spectral response of the detector. With our silicon-based CCD (e.g., DALSA), the effective spectrum is centered around λ = 750 nm, with width Δλ = 300 nm (FWHM). Using the usual formula that supposes a Gaussian shape spectrum:
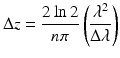
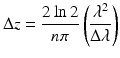
The theoretical axial resolution in a medium with refractive index n = 1.33 (water) is Δz = 0.5 μm. We have experimentally measured 0.7 μm as can be seen on Fig. 25.2.
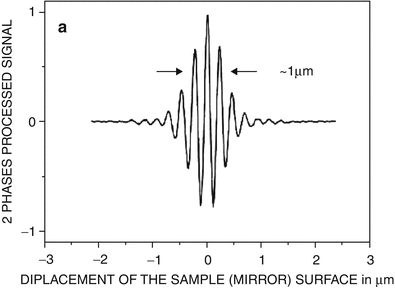
Fig. 25.2
Axial response of the Linnik interferometer (silicon camera, tungsten source)
If dispersion mismatch occurs in the two arms of the interferometer, the axial resolution is degraded. Since biological tissues are constituted mainly of water, the use of water immersion or silicone oil microscope objectives minimizes dispersion mismatch.
What Are the Parameters that Limit the FFOCM Sensitivity?
In general when using a standard tungsten halogen illuminators, we are not limited by the light level impinging the camera; indeed, we can work close to the saturation level for an optimum signal-to-noise ratio. More precisely the important parameter is the amount of electrons stored during the acquisition time. In order to get the maximum signal-to-noise ratio, one must optimize the following performances of the camera:
The images close to the saturation level must be shot noise limited. The test for that is that the difference between two successive identical images must be much higher that the difference between two dark images (see Appendix).
The full-well capacity W must be as high as possible (typically between 100,000 and 1,000,000 of charges for silicon cameras and around 1,000,000 for InGaAs cameras).
Both for the signal-to-noise ratio and to be able to perform in vivo experiments, we need frame rate higher than Fr = 150 frames/s.
The digitalization must be achieved with at least 10 bits in order to avoid sampling errors.
The number N of pixels that we currently use today is one to four million for silicon cameras and 250,000–500,000 for InGaAs cameras.
The camera must be equipped with an external trigger or at least an internal trigger in order to synchronize the image acquisition with the piezoelectric modulation of the path difference.
To summarize our overall quality factor Q for maximizing the signal-to-noise ratio, Q = W.Fr.N; it represents the amount of charges that can be stored during one second on the camera chip.
In order to increase the signal-to-noise ratio, the reference arm mirror must have a reflectivity that ensures a reference power equal or higher than all the incoherent light impinging the camera (light diffused by the sample that is function of the numerical aperture, or stray light of the setup).
As discussed in the Appendix, the images are mainly shot noise limited and one can show that a detection sensitivity of the order of 90 dB (R min = 10−9) can be obtained by accumulating images during a full acquisition time of less than a second.
25.2.2 FFOCM: The LLTech Research Setup
In 2011, LLTech, an ESPCI ParisTech spin-off, has launched the first FFOCM system for clinical research applications (Fig. 25.3).
Fig. 25.3
Picture of the LLTech light CT scanner
This system is based on the principle that we have described but it contains a number of improvements that are necessary in the framework of clinical research:
It is a “plug-and-play” system, for instance, the zero path difference, which is often tricky to find in a Linnik configuration (1 μm position with 10 cm long arms!), is automatically positioned.
The field of view that is required for pathology is typically of the order of 1″ (2.5 cm) in diameter whereas the standard field of view of the cameras using 10× objective is close to 1 mm. Stitching of elementary sub-images is then required to make such large images; because the transverse resolution is 1.4 μm (sampling 0.7 μm/pixel), it is possible to zoom in and out in these large images that are recorded in about 5 min.
For ex vivo experiments, the sample is placed in its sample holder and gently pressed against a transparent window. Incorporation of a liquid avoiding sample drying is ensured.
When exploring a sample in depth, the following problem has to be solved: the refractive index of the tissue being generally different from the immersion liquid index, there is a shift between the focus and the zero path difference (coherence volume) as can be seen on Fig. 25.4 [14–16].
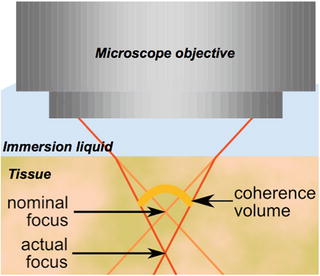
Fig. 25.4
The refractive index mismatch between the immersion liquid refractive index and the tissue refractive index induce a shift between the coherence volume and the focus (From Jonas Binding PhD defense, Paris 2012)
When this shift turns to be larger than the depth of field (e.g., 8 μm for 0.3 NA water immersion objectives), one can observe a reduction of the signal and a degradation of the image quality. The software that drives the system motors automatically compensates for this shift. For ex vivo or in vivo samples, at the end of the sample arm is the biological tissue to be imaged. It could be placed within a specific sample holder. Usually one explores either a large field of view obtained at a few depths or a stack of tomographic images of smaller lateral size.
Finally the LLTech system being designed to be placed in a research hospital environment, the images are available using DICOM data format that is a standard in medical imaging for handling, storing, printing, and transmitting information.
25.2.3 Improving the Available Depth Using InGaAs Cameras
In order to extend the capabilities of the full-field OCM technique and to improve the penetration, an infrared InGaAs FFOCM system has been developed [11, 17, 18]. Indeed in biological tissues there is a decrease in scattering coefficient with increasing wavelength.
For FFOCM tissue imaging systems, the camera detection sensitivity range is the limiting factor and silicon-based cameras are used to probe the 600–1,000 nm wavelength region. For wavelengths >1,000 nm, indium gallium arsenide (InGaAs) chips allow a detection range in the 900–1,700 nm band.
Results presented here have been carried out using silicone oil immersion instead of water. This type of configuration has seemingly not been used in the past.
An infrared beamsplitter was used but microscope objectives were not optimized for this particular wavelength range: we only replaced Olympus 10× objectives by Zeiss 10× ones because their transmission is better above 1 μm. The InGaAs camera (Xeva-1.7-640c, Xenic, Leuven, Belgium) has been mounted onto the full-field OCT setup described on Fig. 25.1. This InGaAs camera full-well capacity (the largest charge that the camera can hold per pixel before saturation) is larger than two million e− with and a frame rate of 25 Hz.
Water absorption spectrum is a major limitation when imaging at wavelengths higher than 1.25 μm (the working distance of the objective being about 3 mm, 6 mm of water has to be considered).
Silicone oil refractive index is about 1.41, which limits its usage to medium numerical aperture water immersion objectives (typically NA <0.35 unless spherical aberration would limit the transverse resolution). Nonetheless, it allows an almost full transmission from 0.9 up to 1.6 μm except for two absorption bands as shown on Fig. 25.5.
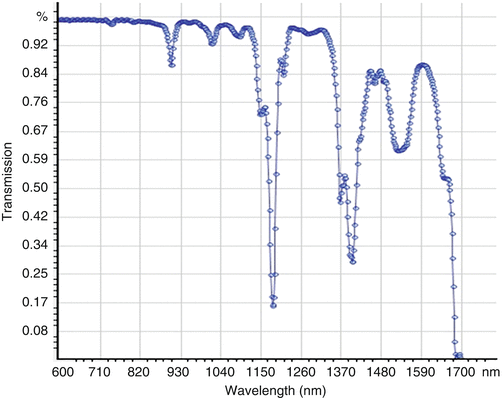
Fig. 25.5
Near-IR transmission of silicone oil (1 cm path)
Indeed, the advantage of silicone oil can be appreciated by comparing the number of fringes observed on a mirror when measurements are performed in oil immersion (about three periods, FWHM) for the near-infrared setup (InGaAs) in comparison to water immersion (about eight periods, FWHM).
In comparison to a configuration with silicone oil in the visible range (i.e., CMOS camera), the spectral bandwidth achieved by the InGaAs setup is significantly larger (i.e., ∼ 600 nm vs. 150–200 nm), but the central wavelength being about two times larger, the theoretical axial resolution is approximately similar to what we get using silicon cameras (around 1 μm). However, the gain lies in the effective spectrum achieved with silicone oil immersion and therefore a gain in penetration depth. The high absorption of water above 1,100 nm is thus drastically reduced by the oil immersion medium in both arms, allowing to fully benefit from the near-infrared part of the polychromatic light source. Recently, Dubois’s group compared two similar FFOCM configurations (both silicon and InGaAs cameras) but within water as immersion medium showing limited or no gain in the near-infrared range [18].
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
