Fig. 21.1
External cavity laser with reflective Fabry-Perot MEMS tunable filter
Many rapidly swept lasers exhibit a preference for tuning short to long wavelength [4–6]. They have higher power and are more stable in that direction. This behavior has been attributed to four-wave mixing in the gain medium [6, 7] coupled with the Bogatov effect [8]. Computer simulations have predicted this red tuning behavior and laser pulsation under some conditions [7] and mode locking in some configurations [9]. We have shown both experimentally [3] and theoretically that sweeping the laser rapidly induces passive mode locking in the Axsun laser. Here we describe the basic dynamics of the laser.
Rapidly swept lasers tune too quickly for lasing to build up anew from spontaneous emission at each new wavelength [10]. A nonlinear optical mechanism is required to shift the wavelength of light circulating within the laser cavity to match the wavelength of the filter on successive round trips. In the case of the Axsun laser, a Doppler shift from the moving MEMS filter mirror does part of the job, although it is small compared to the wavelength shift required. Most of the shift comes from self-phase modulation induced by depletion of the gain as the mode-locked pulse travels through the semiconductor gain medium. Gain depletion is accompanied by a rise in refractive index. The coupling between the index and the power gain can be described using the linewidth enhancement factor, α, as
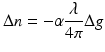
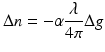
The mode-locking process is illustrated in Fig. 21.2. The SOA becomes optically longer as the pulse travels through, red shifting the light field. The laser does not tune continuously, but rather hops discretely to the next wavelength on each new pulse. The frequency hop for a SOA of length l is
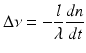
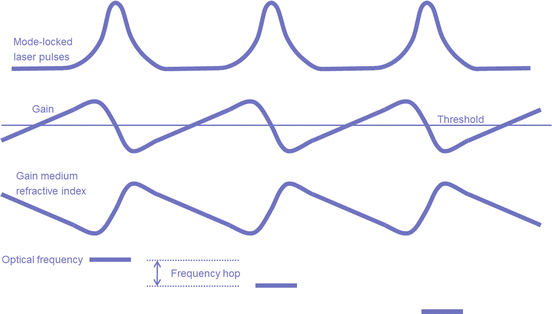
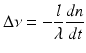

Fig. 21.2
Mode-locking and frequency hopping dynamics of a rapidly swept laser
The pulse energy and width determine the magnitude of the frequency hop. The laser operates in this manner because the lowest threshold is obtained when the pulse frequency hops to follow the filter tuning. A feedback mechanism built into the laser dynamics naturally ensures the pulse hops to follow the filter. In the swept steady state, the pulses are tuned slightly to the long wavelength side of the filter and away from the reflection peak. If a pulse gets ahead of the filter (gets too red), it is attenuated by the filter and the lower power ensures the next pulse does not hop as far. Similarly, if a pulse falls behind (gets too blue), it becomes more powerful and catches up with the filter.
The filter line width and sweep rate play a critical role in ensuring proper mode-locking behavior throughout the sweep. The MEMS filter sweep is linearized to provide a nearly constant sweep rate during the tuning cycle. Stable passive mode-locking behavior can be maintained over the 100 nm data collection range of the laser with a total sweep range of 110 nm. This is essential for obtaining low relative intensity noise (RIN) and maintaining clean k-clocks for the optical engine.
We have developed a theory of these rapidly swept lasers, building on the mode-locking work by Haus [11]. This theory describes this mode-locking behavior in detail and can accurately predict a variety of laser characteristics, such as coherence lengths, as indicated in Fig. 21.3 below, and coherence revival properties, as discussed in the next section.
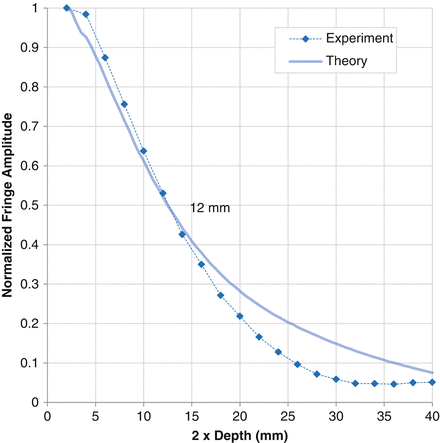

Fig. 21.3
Coherence length measurement compared with mode-locking model calculation
The upper limit of the coherence length of the mode-locked swept laser is determined by the pulse width. Theory predicts considerable chirp to the pulses, reducing the coherence lengths below this upper limit. The coherence length of these lasers is typically 12 mm, which ensures deep imaging capability required for many applications.
21.3 Coherence Revival
The 1,060 nm, 100 kHz laser operates with two pulses traveling in the cavity at once, with the two pulses separated by half the cavity roundtrip time. This can be seen with a high-speed detector and oscilloscope. Normally, an OCT interferometer is set up for short path mismatches, where laser pulses are interfering with themselves. With longer path mismatches, pulses can interfere with their neighbors, leading to the “coherence revival” phenomenon [12]. This behavior is shown in Fig. 21.4. The physical cavity length is 104 mm, but there is also interference at 52 mm due to the double pulsation. A pulse two away is an amplified copy of the first, whereas an adjacent pulse is not. There are two semi-independent pulse trains inside the cavity, leading to a 52 mm coherence function revival that is weaker than the revival at 104 mm.
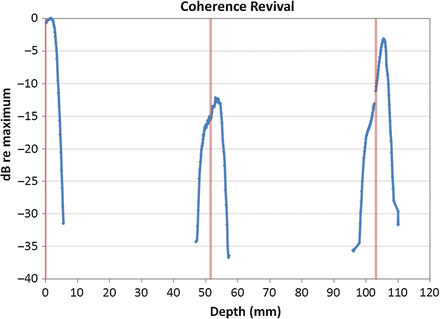

Fig. 21.4
Coherence function of the laser over a wide depth range showing the coherence revival phenomenon. The red vertical lines show the depths where the electrical signal frequency is zero. This measurement was made using an engine with a limited detector bandwidth, so the roll off of the curves reflects the detector bandwidth rather than the coherence length of the laser
Coherence revival is important because it can be a source of artifacts in an OCT system. An OCT interferometer needs to be carefully designed so that small stray reflections are not separated by intervals of half-cavity lengths, 52 mm, 104 mm, 156 mm … etc., where they can produce artifacts in the OCT image.
Coherence revival has also been used to advantage to extend the imaging range of an OCT system [12]. Figure 21.4 shows that the 104 mm peak is displaced from the zero beat location. This means that the signal first goes up with depth before eventually rolling off. The imaging range, which normally is limited by the coherence length, is effectively doubled for this laser when operating at interferometer path mismatches near the 104 mm coherence revival peak. This coherence peak shift is a consequence of the pulse chirp and is a property of this particular laser design. By modifying the cavity design, it is possible to produce sources that do not have this behavior.
21.4 OCT Engine Design
The OCT engine consists of the swept laser module along with control electronics, a calibration k-clock, detection/receiver electronics, and a data acquisition board which samples on k-clock transitions. The engine is designed to simplify construction of OCT imaging systems; the end user provides the optical probe/interface, application control electronics, computing, and specialized software. Figure 21.5 shows a block diagram of the OCT engine.
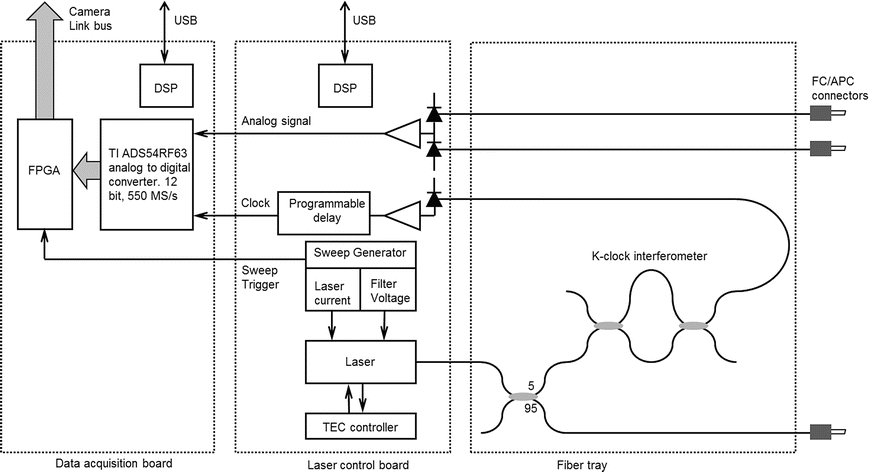

Fig. 21.5
Block diagram of the Axsun OCT engine
The laser control board drives the SOA and MEMS tunable filter. The SOA current and filter drives are controlled through a file stored in flash memory. The control file specifies the SOA current and filter voltages as a function of time. In addition, the board contains two optical receivers. The first is for the calibration k-clock. The k-clock serves as an external clock input to the data acquisition (DAQ) board analog to digital (A2D) converter. A balanced receiver detects light from the main OCT imaging interferometer. The balanced receiver output, k-clock, and sweep trigger are differential signals for noise immunity and are run between the boards over SATA cables commonly used for disk drive interfaces.
In swept-source OCT, it is necessary to translate the raw OCT signal from one that is evenly spaced in time to one with data points evenly spaced in optical frequency, or k. This is often done through various software resampling approaches that interpolate the raw OCT signal. The resampling coefficients can be derived at predetermined intervals or on every A-line, depending on the stability of the swept source and the required imaging accuracy. Either way, the raw OCT signal must be resampled during each A-line.
An alternative approach, and the one used in the Axsun OCT engine, is to use a digital k-clock [13, 16]. The k-clock is derived from a fiber-based Mach-Zehnder interferometer (MZI) as shown in Fig. 21.5. As the laser source sweeps across its wavelength tuning range, the MZI receiver has zero-crossings that are evenly spaced in optical frequency. The MZI path length difference must be four times the maximum imaging depth (interference length = 2 × depth) in order to satisfy the Nyquist sampling limit. This approach speeds up data acquisition by eliminating the computing time for external resampling. However, this approach requires the A2D converter to handle a wide range of k-clock frequencies and duty cycles due to the nonlinear sweep dynamics of the laser.
The data acquisition card in the Axsun OCT engine utilizes a 12-bit Texas Instruments ADS54RF63 analog to digital (A2D) converter. This chip is very tolerant of varying clock frequencies and duty cycles. Its clock specification is 40–550 MHz. We have verified that the DAQ card performs up to the limits of the chip. The FPGA presents the glue logic between the A2D converter and the Camera Link bus. The Camera Link bus can be set to run at 83.3, 41.7, 20.8, or 10.4 MHz. Two 12-bit samples are issued per clock cycle. There is no on-board data storage, but there is an FIFO buffer that mediates between the incoming variable data rate samples and the fixed rate Camera Link output samples. The engine must fill the FIFO faster than it is emptied and must not issue more samples than can be transferred between sweep trigger pulses. The system described in this chapter runs the Camera Link bus at 83.3 MHz. The laser is swept to keep the k-clock frequency greater than 167 MHz, so the FIFO is never empty. At the 100 kHz sweep rate, it transfers 1,376 out of a maximum of 1,670 samples.
The fiber Mach-Zehnder k-clock interferometer is located in the fiber tray. It is precisely cut and fusion spliced to set the maximum depth (Nyquist fold over distance) to an accuracy of ±100 μm. Figure 21.6 shows a picture of the OCT engine stack.


Fig. 21.6
Physical construction of the Axsun OCT engine
Both laser control and DAQ boards can communicate with a personal computer via USB interfaces. A control program, OCTHost, is provided, but customer software can utilize a Windows .NET assembly for custom control.
21.5 System Performance
The Axsun OCT engine described in this chapter is set up for the scan plan in Fig. 21.7. The maximum imaging depth, set by the k-clock interferometer mismatch, is 3.7 mm. The laser sweeps over 110 nm at 100 kHz sweep rate. One thousand three hundred and seventy-six (1,376) samples are acquired, which represents 100 nm of data out of the 110 nm sweep. Although the laser power output is not flat across the sweep, imaging depth resolutions very close to the limits imposed by the pre-FFT window function are obtained. All of the data presented here use a Hann window, though other windows can be chosen to trade resolution for side mode suppression. Calculated theoretical resolutions at 3, 10, and 20 dB from the point spread function peak are listed in the table.




