(1)
Superlum Diodes Ltd., Vvedenskogo N 3, Moscow, 117342, Russia
Contrary to laser diodes, the way of superluminescent diodes (SLDs) to their wide use in practice was much longer. There was always a certain scientific interest to “superluminescent” light output from laser diode structures slightly below threshold that might be considerably enhanced by “damping” of laser resonator (e.g., by tilting of mesa structures) [1–3]. However, there was no considerable practical interest to such light sources until it was proved that SLDs are the real “light sources of choice” for fiber-optic gyroscopes [4]. Successful use of first SLDs in gyros in the early 1980s, as well as some overestimated market demand for gyros, had considerably intensified SLD design efforts. This resulted in the development of “first generation of SLDs” with gyro-rated output power, a few milliwatt or less in single-mode (or polarization maintain) fiber at 800–850 nm and 1,300–1,550 nm bands. Development of gyro-graded SLDs also gave some additional impetus to their usage as light sources in other prospective sensing systems, such as Faraday effect electric current sensors, distributed Bragg grating sensor systems, and some others.
The “second wave” of interest to SLDs as light sources came after successful demonstration of OCT technique and its advantages comparing with other probing techniques in medicine, as well as in other applications [5]. OCT required much more powerful SLDs than those existed in the earlier 1990s, particularly with output power of at least 10 mW from SM fiber with still wide and flat optical spectrum of few tens of nanometers. At the same time, other new applications for such SLDs appeared, for example, testing of fiber-optic telecom components (including WDM/DWDM). This additionally intensified design efforts, which resulted in the development of SLDs with outputs comparable to that of laser diodes, thus ensuring their successful usage in applications where high spatial but low temporal coherence is required.
Each application has its own specific requirements to SLD performance parameters, but OCT requirements are the most hard to meet. The main reason for this is the fact that high optical power, very wide-spectrum, and negligible parasitic spectral modulation must be realized simultaneously. From this point of view, OCT may be considered as “the main driving vehicle” for significant improvement of SLD performance and for developing of new approaches to increase SLD power and decrease coherence length. We will overview and discuss the main principles of developing of powerful broadband SLDs and their performance parameters. Some important aspects of SLD use in practice will be discussed. We will also describe ultra-low-coherence light sources based on the combination of different SLD modules. Possibilities for further improvement of SLDs and SLD-based light sources will be discussed as well.
17.1 Main Principles of SLD Operation and SLD Spectrum Broadening
The unique property of superluminescent diodes is the combination of laser diode-like output power and brightness with broad, LED-like, optical spectrum. Such combination is allowed by high optical gain and wide gain spectrum in semiconductor laser materials.
In fact, any “ideal” SLD is optimized traveling wave semiconductor optical amplifier (SOA) with zero reflections from the ends of active channel (“end reflections” below). In every SLD, two counterpropagating beams of amplified spontaneous emission are traveling along the active region. For estimation of its output power, SLD may be described relatively well by a simple model that does not take into account spectral effects and considers uniform distribution of carriers’ density in SLD active region [6, 7]. Stationary distributions of photon densities in each direction, carrier density, and driving current density are described by well-known rate equations of traveling wave laser diode amplifier [6, 7]:
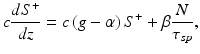
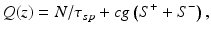
where S + and S − are photon densities of forward and backward propagated waves in active region, g is modal optical gain, α is non-resonant optical losses of waveguided mode, β is fraction of spontaneous emission coupled into guided mode, N is carrier density, τ sp is spontaneous lifetime, Q is driving current density, and c is the velocity of light.
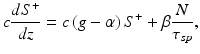
(17.1)
(17.2)
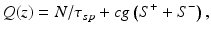
(17.3)
Equations 17.1–17.3 may be solved analytically assuming that carrier density is constant across the active region [6], that should be a good approximation in the case of superluminescent diodes, at least with reasonable (1.5 mm or less) length of active region. In such a case, SLD output power P +(O) on the “output end” of active region of the length L and residual end-reflection coefficients R out and R b may be expressed from Eq. 17.1 as
![$$ {P_{out}}^{+}(O)\propto {S}^{+}(O)={R}_b{S}^{-}(L) \exp \left[\left(g-\alpha \right)L\right]+\frac{\beta N}{c{\tau}_{sp}}\frac{ \exp \left[\left(g-\alpha \right)L\right]}{g-\alpha } $$](/wp-content/uploads/2017/03/A76297_2_En_18_Chapter_Equ4.gif)
and SLD power P −(L) on the back end of the active region may be expressed as
![$$ {P_{back}}^{-}(L)\propto {S}^{-}(L)={R}_{out}{S}^{+}(O) \exp \left[\left(g-\alpha \right)L\right]+\frac{\beta N}{c{\tau}_{sp}}\frac{ \exp \left[\left(g-\alpha \right)L\right]}{g-\alpha } $$](/wp-content/uploads/2017/03/A76297_2_En_18_Chapter_Equ5.gif)
(17.4)
(17.5)
In case of “ideal SLD,” end-reflection coefficients are zero and SLD output power is expressed as
![$$ {P_{out}}^{+}(L)=h\upsilon\;\Pi c{S}^{+}(L)=h\upsilon \Pi \frac{\beta N}{\tau_{sp}}\frac{ \exp \left[\left(g-\alpha \right)L\right]-1}{g-\alpha }, $$](/wp-content/uploads/2017/03/A76297_2_En_18_Chapter_Equ6.gif)
where Π is the cross-section of active region.
(17.6)
For simple estimations, linear dependence of modal gain on carrier density may be used, i.e.,
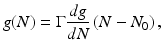
where Γ is optical confinement factor.
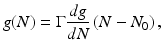
(17.7)
Expressions (17.6) and (17.7) allow to estimate optical gain required to get high output powers. Particularly, considering SLD at 850 nm, carrier density N = 2 × 1019 cm−3, transparency threshold N 0 = 5 × 1017 cm−3, differential gain dg/dN = 0.5 × 10−16 cm−2, optical confinement factor Γ = 0.3, spontaneous emission factor β = 5 × 10−4, τ sp = 2 ns, size of optical mode 0.3 × 5 μm, losses α = 5 cm−1 and length of SLD active waveguide of 1 mm, net gain G = exp[(g−α)L] of ∼30 dB is necessary to realize output power of 30–50 mW. Similar gain is required to make powerful SLDs at other wavelengths.
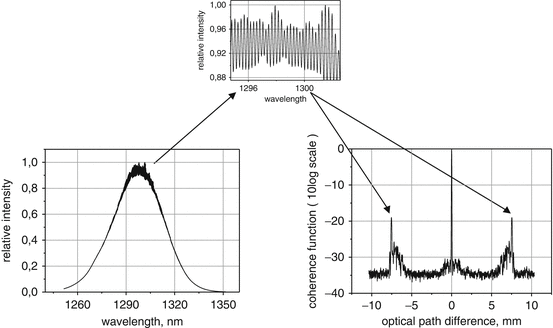
However, it is practically impossible to achieve zero reflections from the ends of semiconductor optical amplifiers due to high reflection coefficient of as-cleaved semiconductor crystals. Such residual reflections always result in parasitic Fabry-Perot modulation (so-called spectral ripple) with period and depth determined by length of amplifier, optical gain, losses, and reflection coefficients. This parasitic modulation results in so-called secondary coherence subpeaks in coherence function, as it is shown on Fig. 17.1. Averaged spectral modulation of 2–4 % usually results in intensity of correspondent secondary coherence subpeak of −25…−20 dB that may cause problems in OCT systems due to correspondent “ghost” images. In case of low modulation index, parasitic Fabry-Perot modulation depth of SLD spectrum may be expressed as [8, 9]
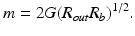
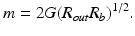
(17.8)
Fig. 17.1
Residual Fabry-Perot spectral modulation in SLD centered around 1,300 nm and correspondent secondary coherence subpeaks
Comparison of (17.6) and (17.8) leads to one of the most important properties of SLD performance that is linear increasing of SLD spectral ripple with output power. In fact, both power and residual spectral modulation indices depend linearly on net gain G (6,8) because N>>N 0 (17.7) and g>>α in all high-power (i.e., high optical gain) SLDs.
Let us now estimate values of end reflections from SLD active region that are necessary to keep residual spectral modulation at low level. As it was pointed out above, net optical gain around 30 dB is required to produce output power of few tens of milliwatt per facet in single-transverse-mode SLDs. Therefore, product R out R b must be as low as 10−10 (i.e., 10−5 per “reflective end”) in order to keep residual spectral modulation in a range of 1–2 % in high-power SLDs.
This is very hard to do such low residual reflections in laser diode materials. Reflection coefficient of as-cleaved crystal facets in most of laser diode structures at 600–1,600 nm is around 0,35. Although a possibility for reaching of 10−5 residual reflection coefficient in AR-coated laser diode crystals was demonstrated in [10], in practice, all SLDs made by AR coating of laser diodes show very strong, 10 % and much higher, residual Fabry-Perot ripple starting some “low-to-moderate,” 3–5 mW, output power per facet (see, e.g., [11, 12]; to our knowledge, there are no reports about SLDs based on AR-coated lasers with better performance parameters). Most probably, the reason for why it is impossible to do even “low-to-moderate” power low-rippled SLDs by simple antireflection coating of laser diode crystals is that required residual reflection cannot be realized technologically on big lots due to minor lot-to-lot variations of center wavelength and far-field divergence in laser diode structures. The problem of high spectral ripple in SLDs based on AR-coated laser diodes resulted in the development of specific SLD geometries that allowed strong damping of residual “end reflections.”
All low-rippled SLD geometries may be divided into two main categories: so-called “angled” (tilted, slanted) structures, where active waveguide is tilted to SLD crystal facet [2], and structures where ends of SLD active region are followed by relatively long “transparent window” regions and/or integrated absorbing region on the back side of SLD waveguide [7]. All modern powerful and low-rippled SLDs are based either on “tilted” or “transparent window” or “integrated absorber” designs, or on their combinations [see, e.g., 13–17].
But even after the problem of end reflections is solved on “design level” by appropriate SLD geometry, it is still necessary to apply antireflection coating on at least output facet of SLD crystal. Although “simple” AR coating may be used for medium-power SLDs, specific coating, that is not only antireflective but also protective, should be used in powerful diodes, especially in AlGaAs-based SLDs (AlGaAs is known for its relatively low catastrophic optical damage, COD, threshold). This problem may be solved by double-layer coating of output facet with the first layer working as protective layer and finishing layer optimized for best antireflection properties of resulted multilayer structure [18].
Let us now consider spectrum width of SLDs. Obviously, SLD spectrum is determined by the width of optical gain spectrum of active media. Optical spectrum width of the first SLDs, all based on bulk semiconductor heterostructures with relatively thick active layer, varied from (typical) 15–20 nm in 850 nm AlGaAs emitters to 30–40 nm in 1,300–1,550 nm InGaAsP SLDs. Although some exotic designs were proposed to broaden spectrum of “bulk” active layer SLD (particularly “stacked-layer-SLD” with two active layers with different material composition [19]), the real progress in SLD spectral broadening started after successful demonstration of quantum-well (QW) SLDs in [20].
Spectral broadening in QW SLDs is based on two main principles. The first one is a possibility for spectral broadening of optical gain due to very high density of states in QW structures with respect to bulk structures in case of the same driving current density [20]. Additional possibility for spectral broadening appears when transitions from different subbands in QW active layers are utilized to produce SLD output [21, 22]. Particularly, in single-quantum-well (SQW) AlGaAs laser structures, transitions from two, n = 1 (sometimes called “ground state”) and n = 2 (sometimes called “excited state”), states in conductive band are possible [21]. While output power of only 3 mW and 50 nm spectrum width was realized in [20] for the first time from QW SLDs at 850 nm, it was shown in [22] that optimization of SLD active length and geometry allows additional spectral broadening by simultaneous amplification at n = 1 and n = 2 transitions and further increasing of SLD power; spectrum width of 70 nm was realized at 10 mW output power. Possibility for considerable spectral broadening by MQW (multiple-quantum-well) SLDs at longer wavelength (1,550 nm) was also demonstrated for the first time in [22]. Nowadays most of powerful and broad-spectrum SLDs at all spectral bands are based on SQW or MQW structure.
It should be pointed out, though, that SQW/MQW SLD spectrum width may depend on drive current much stronger than that of bulk SLD. Particularly, in bulk AlGaAs/GaAs heterostructures, spectrum width of optical gain is usually around 20 nm (around room ambient temperature; it may depend slightly on material composition and active layer doping, see, e.g., [23]). This is why all ever-reported bulk active region AlGaAs SLDs had spectrum width of 15–20 nm with weak dependence of spectrum width on drive current. In SQW/MQW SLD, spectrum width depends on drive current much stronger [21, 22]; particularly, it was broadened by 2–3 times in 820 nm and 1,550 nm SLDs reported in [21, 22] but became strongly non-Gaussian reaching its widest value at some “fixed” value of output power and driving current. Spectral shape of such SLDs is usually “double humped” due to energy separation between different subbands in quantum wells. Changing of driving current results in domination of one of the spectral maxima and narrowing of optical spectrum. Note also that complex form of spectrum may result in strong distortions of coherence function. Figure 17.2 shows main autocorrelation maxima of “bulk” and broadband SQW AlGaAs SLDs. Though some negligible distortions of coherence function due to spectrum asymmetry are seen in bulk SLD, they are much less than that of SQW SLD with very wide but double-humped spectrum.
Fig. 17.2
Spectrum and coherence functions of bulk (1) and SQW (2) SLDs at 820 nm band. It is seen that unless SQW SLD coherence function is much narrower, sidelobes in main autocorrelation maximum of bulk SLD with Gaussian spectrum are well below –15 dB and are roughly 10 dB less than that of SQW SLD with “double-humped” spectrum
During the last couple of few years, a possibility of further broadening of SLD spectrum by using quantum dot (QD) structures had been studied [24–26]. Principle of spectral broadening in QD structures is similar to that in QW structures. Considerable broadening is obtained when optical gains at “ground state” and “excited state” in QDs are equal. Additional broadening of entire spectrum is possible due to considerable fluctuation of dots size in today’s QD structures. Electroluminescence covering almost 350 nm had been reported in QD structures centered at ∼1,200 nm [27]. However, performance of QD SLDs reported so far (which will be reviewed below) is comparable with that of QW SLDs (in terms of combination of high power and wide spectrum, although wider spectra were demonstrated at low levels of output power).
17.2 Reported SLD Performance Parameters
In this chapter we will review main achievements in development of very high-power and broad-spectrum SLDs at different spectral bands. The main attention will be paid to SLD output power and spectrum width, but some other issues like far-field, polarization, and noise will be discussed as well.
17.2.1 AlGaInP SLDs at 680 nm
Output power up to 4 mW was realized from bulk SLD [15]; output power was increased considerably, up to 50 mW, by using MQW active layer [28]. However, spectrum width of only 8–10 nm was reported in both publications. Commercially available SLDs have the same width of spectrum and output power of up to 5 mW from SM fiber.
17.2.2 AlGaAs SLDs at 780–870 nm Band
A lot of powerful SLDs at this spectral band had been reported. Output power of ∼100 mW before COD was successively demonstrated in [18, 29]. It was also shown in [30] that COD threshold may be increased considerably by adding of short unpumped regions near SLD crystal facets. Free-space output power 250 mW per facet was realized by optimization of the length of such regions. SM fiber output power in excess of 100 mW was realized from such SLDs by coupling via cylindrical microlens on the fiber end. Such output power is comparable with powerful single-mode fiber-coupled laser diodes at this band.
In QW SLDs, output power up to 100 mW with 50 nm FWHM was realized by optimization of SLD structure and length of active region [28]. Commercially available SLDs at this spectral band now produce up to 30 mW output with up to 60 nm spectrum width. This spectrum width corresponds to coherence length in the air of less than 10 μm.
Possibilities to realize much broader spectrum in 820 nm SLDs were also demonstrated in [31, 32]. In [31], 100 nm averaged spectrum width was obtained by combined DC and pulse driving of SQW SLD. In [32], up to 90 nm spectrum width was obtained in SLDs with MQW active layer consisted of four layers with thickness varied from 2 to 12 nm. Though reaching of 100 nm spectrum width will allow ultrahigh-resolution OCT at 850 nm band by “single-SLD-emitter” light source, until now there are no commercially available powerful SLDs at 820 nm band with spectrum width exceeding 65 nm.
17.2.3 InGaAs SLDs at 920–1,060 nm Spectral Band
Very broad-spectrum and very high output power had been demonstrated for InGaAs SLDs at 920–980 nm, too. In [9, 28], output power in excess of 100 mW was reported for SLDs around 960–980 nm with bell-like spectrum with approximately 25–30 nm spectrum width and 70 nm wide spectrum with output power around 30 mW. Later, 100 nm spectrum width was realized from optimized QW SLD at 920 nm with free-space output power up to 30 mW (>10 mW ex SM fiber) [33]. Commercial SLDs emit up to 30 mW (SM fiber) output power with 50 nm wide bell-like spectrum and up to 100 nm wide spectrum and 10 mW SM fiber power.
It should be pointed out again that the most broadband and powerful SLDs at 780–1,000 nm have “double-humped” spectrum as simultaneous emission from different subbands of QW active region is used for spectral broadening. Figures 17.3 and 17.4 show spectrum of single-mode fiber-coupled SLD modules emitting 35 mW at 840 nm with 50 nm spectral bandwidth and 10 mW at 930 nm with 100 nm spectral bandwidth and their coherence functions.
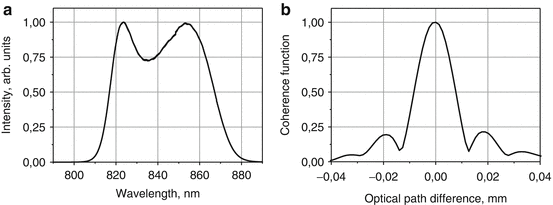
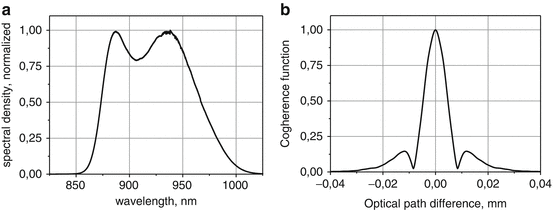
Fig. 17.3
Spectrum and coherence function of 35 mW SM fiber output power QW SLD module at 840 nm
Fig. 17.4
Spectrum and coherence function of 10 mW SM fiber output power QW SLD module at 930 nm
InGaAs/GaAs heterostructures were also used to make SLDs at 1,060 nm, the wavelength of growing interest for OCT [34, 35]. The first SLDs reported at this spectral band had output power less than 10 mW (less than 2 mW ex SM fiber [18]). Output power around 50 mW and spectrum width of 110 nm were demonstrated in SLDs centered at 1,030 nm later [36]. Currently, SLDs with spectrum width of ∼50–60 nm (bell-shaped spectrum) and ∼100 nm (double-humped spectrum) are commercially available.
A possibility of further improving of SLD output power and spectrum width in devices emitting around 1,000–1,060 nm was demonstrated by using of quantum dot (QD) structures. As mentioned above, such structures allow additional broadening of optical gain spectrum due to inhomogeneous dot size distribution in QD active layers. Being a disadvantage to do high-performance QD lasers such “QD dispersion” allows considerable broadening of SLD spectrum [37]. Very broad spectrum had been obtained in SLDs centered at 1,180 nm (up to 150 nm), but SLD power was below 100 μW in this case [38]. However, spectrum width became comparable with that possible by QW structures when shorter wavelengths were targeted. Particularly, free-space output power up to 200 mW with spectrum width around 60 nm was realized in such SLDs centered around 1,000 nm [39].
17.2.4 InGaAsP/InP SLDs at 1,300–1,600 nm Spectral Band
SLDs at this band, especially those centered around 1,300 nm, are very attractive for OCT due to better penetration into tissue. However, increasing of wavelength results in decreasing of coherence length proportionally to square of wavelength. This makes requirements to a long-wavelength SLDs more “stressed” as, for example, spectrum of 1,300 nm SLD must be at least 2.5 times broader with respect to 800 nm counterpart in order to get the same spatial resolution.
Numerous efforts had been put for the development of powerful and broadband SLDs at this spectral band, including optimization of quantum-well (usually multiple QWs) structures and QD structures [26, 39–45]. High output power and wide bell-shaped spectrum had been demonstrated at different center wavelengths. SLD modules with single-mode fiber output of 10–20 mW and spectrum width of up to 80 nm (bell-shaped) and 100 nm (double-hump) are now commercially available.
Let us now discuss briefly other important SLD performance parameters, starting from far-field pattern.
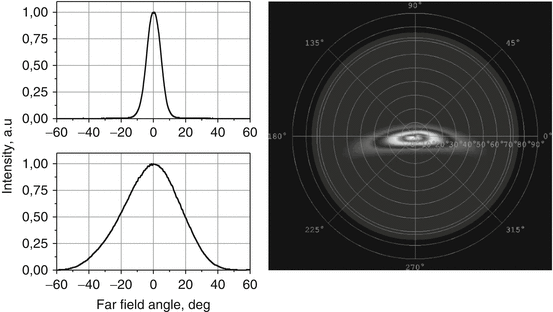
In principle, far field of any single-transverse-mode SLD should be similar to that of conventional single-transverse-mode laser diode (LD) as similar waveguide structures are used in both. However, analysis of SLD literature shows that in most of powerful SLDs active waveguide is tilted to crystal facets. Such tilting results in “crescent” structure of far field, like it is shown on Fig. 17.5 for SLD at 680 nm reported in [28]. Therefore, though conventional LD-graded optics may be used for collimation/focusing of SLD beams, additional optical elements may be required for focusing to diffraction-limited spots. As well, detailed study of spatial coherence [46] shows that even narrow active waveguide SLDs with far-field pattern similar to single-transverse-mode structure may be not 100 % spatially coherent, most probably due to additional high-order mode(s) of lower intensity. From this point of view, SM fiber-coupled SLDs may be more useful also for free-space OCT systems.
