Fig. 36.1
Absorption spectra of common chromophores in human tissue, total tissue absorption, and tissue scattering for biologically normal concentrations (Data obtained from Ref [44]). Scattering is assumed to follow power-law dependence on wavelength μ s = a λ −b
Roughly, the scattering coefficient μ s shows an inverse power-law dependence on wavelength μ s = aλ −b , from which the parameters (a,b) depend on the size distribution, concentration, and relative refractive index of the scattering volume elements (e.g., cell membranes, collagen fibers, mitochondria). A light scattering experiment thus provides information on the structural organization of the probed tissue. A demonstration of this paradigm was given by Van der Meer et al. [15] by determining the attenuation coefficient μ LCI (see Sect. 36.2.2, Eq. 36.8) averaged over the bandwidth of an 800 nm OCT system, of cells forced into apoptosis and necrosis. Both apoptosis, programmed cell death, and necrosis, accidental cell death, are processes that are known to follow a cascade of morphological changes at the (sub)cellular level. The experiment shown in Fig. 36.2 demonstrates that, even though OCT does not have sufficient resolution to directly image processes at the subcellular level, it is still sensitive to the associated morphological changes through changes in light scattering.
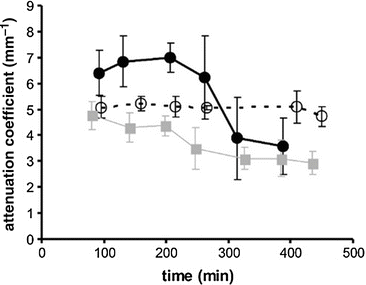

Fig. 36.2
The measured attenuation coefficient for 800 nm light in pelleted human fibroblasts, as a function of time. Time was measured in minutes from the point that the cells forced into necrosis (filled squares) or apoptosis (filled dots). Untreated control cells show no change in scattering (open circles)
A major application of spectroscopic LCI is the quantification of spatially localized hemoglobin concentration and oxygen saturation which, combined with local perfusion measurements, can have significant impact on cancer care. A tumor’s local oxygen status, specifically hypoxia, is considered one of the “hallmarks of cancer” predicting progression and response to therapy. The potential of spectroscopic LCI may be further enhanced by quantification of changes in tissue morphology during disease progression based on spectrally resolved scattering properties. The potential of this method is illustrated in Fig. 36.3, showing in panel A and B in vivo obtained volume rendering resp. individual B-scans of vulvar intraepithelial neoplasia (VIN), a precursor of cancer. Panel C sketches how the signal decay with depth is quantified though the attenuation coefficient μ LCI , a procedure that is detailed in Sect. 36.2.2. Panel D indicates the potential of discriminating between normal and premalignant tissue using μ LCI [16]. Similar results were obtained discriminating between normal kidney tissue and kidney cancer [17, 18].
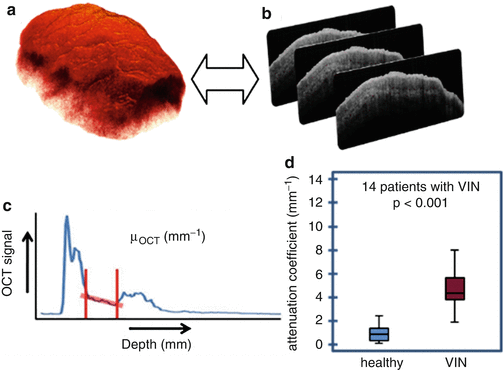

Fig. 36.3
(a) 3D image obtained in the clinic from a lesion suspected for vulvar intraepithelial neoplasia (VIN), a precursor of cancer. (b) Constituting 2D-OCT images of this lesion. (c) The decay of the OCT signal versus depth in a region of interest selected from the images of panel (a) or (b) is determined by fitting a mathematical model of the OCT signal to this data (after careful calibration of the system). (d) Results demonstrating the capability of differentiating between normal and VIN tissues by the attenuation coefficient μ LCI [16]
Despite this application potential, clinical studies have been reported where the measurement of only one parameter (e.g., the value of μ LCI averaged over the bandwidth of an OCT system) was not sufficient to differentiate between different grades (pathologists’ assessment of tumor aggressiveness) of urothelial carcinoma of the bladder [19]. As we discuss in the next sections, spectroscopic LCI provides the possibility of retrieval of not only μ LCI (λ) but also of backscattering coefficients μ b (λ) which shows large sensitivity to morphology.
This chapter starts with outlining the theory of spectroscopic LCI, describing methods to quantitatively obtain localized spectra. This includes computational and instrumental considerations such as proper correction for point spread functions of the LCI equipment. We then discuss the retrievable optical property spectra, e.g., absorption and scattering spectra that can be derived from these measurements and their interpretation in terms of physiologically relevant tissue characteristics. We conclude by presenting clinical examples of spectroscopic LCI.
36.2 Theory
The general form of the detected LCI interferogram is written as:
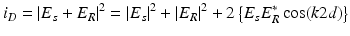
where E S and E R are the fields returning from sample and reference arm, respectively, with wave number k = 2π/λ with λ the wavelength. Further, 2d is the optical path length difference so that d is the assigned depth location in the tissue. Wave number k and optical path length difference 2d form the fundamental Fourier pair in LCI data analysis. Classic time domain detection receives all wavelengths at once, while modulating 2d using a moving reference arm (effectively integrating Eq. 36.1 over k), whereas in Fourier domain OCT, the signal is obtained as function of k, integrating over 2d. The goal of spectroscopic LCI modalities is to obtain information in k and d domains simultaneously, with high resolution in both domains.
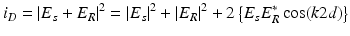
(36.1)
Both 2d-domain and k-domain descriptions of the OCT signal i D are equivalent and are related by Fourier transformation:
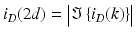
where ℑ denotes the Fourier transform. Since the wave number k is directly related to wavelength λ, wavelength dependent spectra i D (λ) can be obtained from the backscattered LCI signal. We drop the factor “2” going onward and use the concepts “spatial domain” and “depth domain” interchangeably.
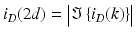
(36.2)
36.2.1 Localized Spectroscopic Information
Time-frequency analysis – Due to wavelength-dependent scattering and absorption by the different structures in tissue, the spectral content of the OCT signal changes with depth. Therefore direct application of the Fourier transform on either spatial or spectral domain detected signal Eq. 36.2 is not appropriate to obtain localized spectroscopic information because the depth resp. wave number varying information will be lost. Instead, spectral analysis methods, conventionally called time-frequency (TF) [20] analysis must be used (or, for the present context, depth-wavelength analysis). In most studies, the preferred method has been to use short-time Fourier transforms (STFT):
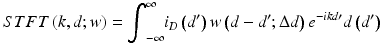
where w is an analysis window confined in space around d with spatial width Δd, for example, a Gaussian function. The multiplication with a relatively short window effectively suppresses the signal outside the analysis point d±Δd. Physically, the STFT can be considered as the result of passing a signal through an array of band-pass filters with linearly increasing center frequency and constant bandwidth which is inversely proportional to Δd. Thus, there is an inherent trade-off between spectral and spatial resolution. A window with short spatial width Δd will localize the signal well in space but will have reduced k-resolution; conversely a signal with long width will be less well localized in space with the benefit of increased spectral resolution. For a Gaussian window, a spatial domain width Δd will yield a spectral resolution of Δk = 1/(2Δd).
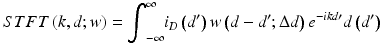
(36.3)
The wavelet transform was introduced to partially overcome this trade-off by adjusting the window size to the frequency being considered. The basic difference between the wavelet transform and the STFT is that the duration and the bandwidth of the wavelet are both changed (while shape remains the same). Physically, the wavelet transform can also be seen as an array of band-pass filters with constant relative bandwidth with respect to the center frequency. In contrast with the STFT, which uses a single analysis window, the wavelet transform uses short windows at high frequencies and long windows at low frequencies. Again, there is a trade-off between time and frequency resolutions. However, these resolutions depend on frequency: the frequency (resp. time) resolution becomes poorer (resp. better) with increasing analysis frequency.
The wavelet transform projects a signal on a family of functions deduced from a (complex) window function w, the “mother wavelet,” by translations and dilations:
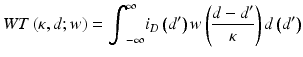
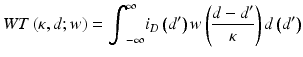
(36.4)
The variable κ is the scale factor, dilating (|κ| >1) or compressing (|κ| <1) the wavelet w. When mother wavelets are used that are well localized around a wave number k 0, then a time-frequency interpretation is possible through k = k 0/κ.
Bilinear TF distributions do not suffer from the resolution trade-off between both domains. The most important member of this class is the Wigner distribution:


(36.5)
The Wigner distribution is the Fourier transform of an autocorrelation measure of the signal i D(d). Whereas in conventional autocorrelation computations, the result is a function of lag only, here the functional dependence on d is maintained. In concordance with the Wiener-Khinchine theorem, the straightforward interpretation of the WD is as a localized power spectral density of the detector signal.
The drawback of the WD lies in its quadratic nature: whereas the STFT of two signals X and Y yields STFT x (k, d) + STFT y (k, d), the WD will contain interference terms, e.g., WD x+y (k, d) = WD x (k, d) + WD y (k, d) + 2Re[WD x,y (k, d)]. Even though the interference term contains information on the separation of X and Y (e.g., in space), when it overlaps with the signal terms, interpretation of the WD becomes challenging. In practice (like with the STFT), the signal is analyzed using a window w. This pseudo-WD effectively smoothens the time-frequency distribution, suppressing the interference terms. However, a short smoothing window will be narrow in time and wide in frequency, leading to a good time resolution but bad frequency resolution and vice versa. It is possible to add a degree of freedom by considering a separable smoothing function Π(k, d) = w 1(k, Δk)w 2(d, Δd) that allows independent control in both time and frequency of the smoothing applied to the WVD; Δk and Δd denote the width of the window functions in the spectral and spatial domain, respectively. The STFT compromise between time and frequency resolution is now replaced by a compromise between the joint time-frequency resolution and the level of suppression of the interference terms. Robles et al. showed that the pseudo-WD can also be obtained by STFT analysis using two k-domain window sizes Δk 1>> Δk 2. The result STFT1(k, d) × STFT2(k, d) is mathematically equivalent to a pseudo-WD with window widths of W 1(k, Δk = k 2/2) in the spectral domain and window W 2(d, Δd = 1/(2 k 1)) in the spatial domain. As for the WD, any remaining interference terms may carry information, for example, on average spatial scatterer separation [7–9].
Xu et al. [21] also define a third class of time-frequency distributions, based on the presumed known spectral profiles of the laser source and the sample. This allows for fitting the obtained OCT signal to this model equation, thereby retrieving the sought spectral properties. In practice, there may exist an optimal time-frequency analysis depending on the application. For example, the STFT is completely free of artifacts such as introduced by the quadratic analysis of the energy distributions. The poor depth resolution resulting from the requirement of a high spectral resolution may not be a problem at all when analyzing relatively large tissue structures, where a spatially averaged spectrum over the entire tissue structure is required. For example, a spectral resolution of 6 nm in LCS corresponds to a depth resolution of 22 μm, which is sufficient to measure hemoglobin concentrations from optical property spectra in distinct regions of the epidermis and the dermis [12] (see Sect. 36.3.2).
Hardware-based approaches and considerations – For proper quantification of local spectra, signal attenuating factors caused by the LCI system need to be accounted for. The two dominating factors are the confocal point spread function (e.g., loss of sensitivity away from the focal region) and the sensitivity roll-off in depth for spectral domain LCI, caused by the finite resolution of the spectrometer (or the finite instantaneous bandwidth of the swept source).
Confocal point spread function – The confocal point spread function (PSF) for a single-mode fiber-based OCT system was derived in [22] and validated experimentally in [23]. It can be directly imaged using OCT on a highly diluted (e.g., negligible scattering) sample.
An example of this procedure is shown in Fig. 36.4 for LCS, in a weakly scattering medium (0.038 vol.% of ø198 polystyrene spheres, μ s <<1 mm−1). The PSF is then given by

where α is a scaling factor, d focus is the geometrical position of the focus in the sample, and Z R is the Rayleigh length of the system (Fig. 36.4b). From Z R , the beam waist can be computed as ω = (Z R λ/2π)½, and from that the NA can be derived, using NA = sin(θ) ≈ sin(λ/(π ω)). In the preceding definitions, Z R ω and NA are defined in the medium, e.g., Z R = nZ 0 where Z 0 is the Rayleigh length of the system measured in air and n is the refractive index. Clearly, the PSF is therefore wavelength dependent. When possible the calibration should be performed wavelength resolved (Fig. 36.4).
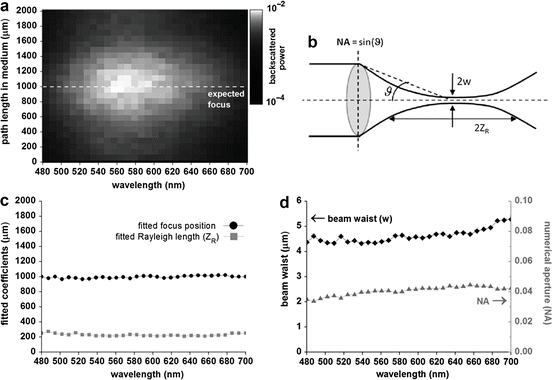

(36.6)

Fig. 36.4
(a) Point spread function measurement (PSF) on a weakly scattering sample of ø198 spheres (0.038 vol.%), (b) schematic illustration of focus geometry, (c) fitted focus position (dfocus) and Rayleigh length (ZR) on the measured PSF, (d) calculated beam waist (ω) and numerical aperture (NA). The parameters ZR, ω, and NA are defined within the medium (n = 1.35)
The confocal PSF can also be exploited to optimize the trade-off between spatial and spectral resolution by restricting the spatial extent of the collected data region. Xu et al. used high-numerical-aperture optics, geometrically restricting the spatial extent of the signal while using long analysis windows to extract high-resolution spectral information [24].
Sensitivity roll-off – SOCT suffers, when using spectral domain detection (Chaps. 5, “Spectral/Fourier Domain Optical Coherence Tomography”, 6, “Complex and Coherence-Noise Free Fourier Domain Optical Coherence Tomography”, and 7, “Optical Frequency Domain Imaging”), from the inherent loss of sensitivity with depth due to the finite resolution of the detecting spectrometer (or the finite instantaneous bandwidth/sampling time in swept-source implementations). This causes unwanted signal attenuation that can, similarly to the confocal PSF correction, be accounted for in post-processing. Here too, the effect can be turned to advantage by limiting the spatial extent of the collected data. Figure 36.5 shows the theoretical and measured roll-off of an LCS system based on a commercially available Ocean Optics USB4000 spectrometer. The “low” spectral resolution of 8 nm of this device results in roll-off function with full width at half maximum of FWHM ∼10 μm, so that meaningful interference signals are only collected in a window of approximately 20 μm around the equivalent position of the reference arm in the sample. Details of spectral domain LCS can be found in [13].
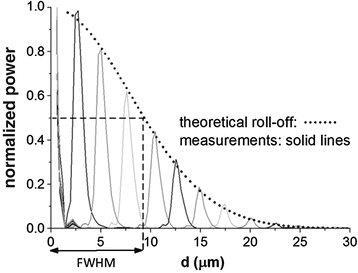

Fig. 36.5
Theoretical and measured sensitivity roll-off of a spectral domain LCS setup using an Ocean Optics USB4000 spectrometer
36.2.2 Quantitative Determination of Optical Properties
Retrievable properties using spectroscopic low-coherence interferometry – In general, all methods described above result in a wavelength-resolved power spectrum S acquired within a depth window Δd around a depth d in the sample. We will indicate all wavelength-dependent parameters in the remainder of this chapter by a bold-faced character. The following theory assumes validity of the 1st Born approximation, e.g., the illuminating field is much stronger than the scattered field. Under this assumption, the LCI signal is formed by single backscattering, so that the amplitude of S (d) decreases exponentially with measurement depth and the attenuation coefficient μ LCI of the sample. Hence, we can describe S (d) using Beer’s law:
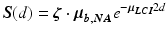
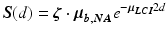
(36.7)
The factor 2 in Eq. 36.7 accounts for round-trip attenuation to and from depth d. We note that if the amplitude E(d) of the LCI signal is considered, rather than backscattered power, this factor drops from Beer’s law since E(d) is proportional to the square root of S (d). We also assume that the influence of the PSF and sensitivity roll-off have been accounted for in preprocessing. The LCI-attenuation coefficient μ LCI is given by
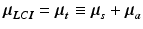
with μ t the attenuation coefficient, defined as the sum of the scattering coefficient μ s and the absorption coefficient μ a . The latter 3 parameters are formally defined in textbooks, e.g. [25], and are discussed in more detail below. We introduce the LCI-attenuation coefficient μ LCI (the experimental outcome) because in practice, even when correction for PSF and roll-off is not (optimally) performed, and/or when the first Born approximation does not hold, a single exponential decay model Eq. 36.7 is often suitable for fitting the OCT system [23]. In these cases, the simple relation of Eq. 36.8 breaks down, i.e., μ LCI ≠ μ t . However, the μ a can still be retrieved because absorption takes place along the photon’s path (regardless of its trajectory), but values for “μ s ” should be interpreted with caution in this case.
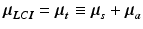
(36.8)
The parameters ζ and μ b, NA determine the amplitude of S (d) at d = 0. The system-dependent parameters are defined by ζ = S 0 ∙ T ∙2Δd, with S 0 the source power spectrum incident on the sample and T the axial point spread function Eq. 36.6. The backscattering coefficient μ b, NA is a sample-dependent parameter, which is defined as the product of the scattering coefficient μ s and the scattering phase function p (θ), integrated over the numerical aperture (NA) of the detection optics:
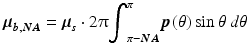
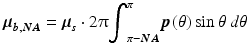
(36.9)
To quantitatively determine the μ b, NA of the sample using Eq. 36.8, knowledge of ζ is required. A method to determine ζ is by a separate calibration measurement on a sample with a known μ b, NA , e.g., using Mie theory on well-defined scattering particles [11].
To determine μ LCI the same calibration measurement may be used, although it is not always necessary since μ LCI can be obtained directly from the slope of the exponential decay between two or more chosen depths d (according to Eq. 36.7, see also Fig. 36.3c). As a consequence, μ LCI can be determined in any depth region of interest. The sample’s attenuation is composed of the losses due to both scattering and absorption. When correcting S (d) for the attenuation, also the μ b, NA can be determined at any depth of interest.
Interpretation of measured properties – The absorption coefficient μ a is directly related to the individual absorption spectra and concentrations of chromophores (e.g., water, hemoglobin, bilirubin) present in the probed volume. The diagnostic value of μ s measurements depends on its relation to tissue morphology and organization. Ideally, tissue classification based on μ s would be highly correlated with classification by the pathologist based on microscopic evaluation. The classic approach is to model tissue as an ensemble of spherical scatterers with an effective size to match the experiment. The scattering cross section σ s and phase function p(θ) are then obtained, e.g., by Mie theory [25]. The scattering coefficient follows from

![$$ {\boldsymbol{\mu}}_s=\frac{f_v}{V}{\boldsymbol{\sigma}}_{\boldsymbol{s}}\left[2\pi {\displaystyle {\int}_0^{\pi }{\boldsymbol{S}}_{\boldsymbol{P}-\boldsymbol{Y}}}\left({f}_v,\theta \right)\boldsymbol{p}\left(\theta \right) \sin \theta\;d\;\theta \right] $$](/wp-content/uploads/2017/03/A76297_2_En_37_Chapter_Equ10.gif)


