(5.1)
with e the electron charge; P ref and P sample , respectively, the reference arm and sample arm power per detector element at the detection arm fiber tip; τ i the integration time; and E v the photon energy.
The readout and dark noise, shot noise, and relative intensity noise (RIN) contributions to the overall noise in electrons squared per read out cycle and per detector element are given by, respectively [6, 7],
![$$ {\sigma}_{noise}^2={\sigma}_{r+d}^2+\frac{\eta\;{e}^2{P}_{ref}{\tau}_i}{E_{\nu }}+{\left(\frac{\eta\;e{P}_{ref}}{E_{\nu }}\right)}^2{\tau}_i{\tau}_{coh}\kern1em \left[{e}^2\right], $$](/wp-content/uploads/2017/03/A76297_2_En_6_Chapter_Equ2.gif)
where the sample arm power was assumed to be much smaller than the reference arm power [22], with σ r + d 2 the sum of readout noise and dark noise and 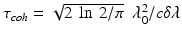 the coherence time, with c the speed of light [23]. The optimal signal-to-noise performance is achieved when shot noise dominates both readout noise and relative intensity noise (RIN) [22]. Shot noise dominates readout noise and dark noise when η e 2 P ref τ i /σ r+d 2 E ν > 1, and shot noise dominates RIN when their ratio is larger than one, i.e., E ν /ηP ref τ coh > 1. The optimal reference arm power is found when readout noise and dark noise are equal to the RIN [24]:
the coherence time, with c the speed of light [23]. The optimal signal-to-noise performance is achieved when shot noise dominates both readout noise and relative intensity noise (RIN) [22]. Shot noise dominates readout noise and dark noise when η e 2 P ref τ i /σ r+d 2 E ν > 1, and shot noise dominates RIN when their ratio is larger than one, i.e., E ν /ηP ref τ coh > 1. The optimal reference arm power is found when readout noise and dark noise are equal to the RIN [24]:
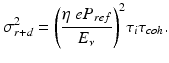
![$$ {\sigma}_{noise}^2={\sigma}_{r+d}^2+\frac{\eta\;{e}^2{P}_{ref}{\tau}_i}{E_{\nu }}+{\left(\frac{\eta\;e{P}_{ref}}{E_{\nu }}\right)}^2{\tau}_i{\tau}_{coh}\kern1em \left[{e}^2\right], $$](/wp-content/uploads/2017/03/A76297_2_En_6_Chapter_Equ2.gif)
(5.2)
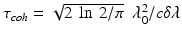 the coherence time, with c the speed of light [23]. The optimal signal-to-noise performance is achieved when shot noise dominates both readout noise and relative intensity noise (RIN) [22]. Shot noise dominates readout noise and dark noise when η e 2 P ref τ i /σ r+d 2 E ν > 1, and shot noise dominates RIN when their ratio is larger than one, i.e., E ν /ηP ref τ coh > 1. The optimal reference arm power is found when readout noise and dark noise are equal to the RIN [24]:
the coherence time, with c the speed of light [23]. The optimal signal-to-noise performance is achieved when shot noise dominates both readout noise and relative intensity noise (RIN) [22]. Shot noise dominates readout noise and dark noise when η e 2 P ref τ i /σ r+d 2 E ν > 1, and shot noise dominates RIN when their ratio is larger than one, i.e., E ν /ηP ref τ coh > 1. The optimal reference arm power is found when readout noise and dark noise are equal to the RIN [24]: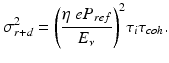
(5.3)
Thus, for a system to operate close to shot noise limited performance, shot noise should dominate thermal and RIN at the optimal reference arm power:
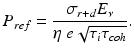
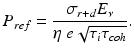
(5.4)
At this optimal reference arm power, the inequalities describing shot noise dominance over readout noise and RIN, respectively, reduce to the same equation:
![$$ \frac{\;e\sqrt{\tau_i}}{\sigma_{rd}\;\sqrt{\tau_{coh}}}>1. $$
” src=”/wp-content/uploads/2017/03/A76297_2_En_6_Chapter_Equ5.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(5.5)</DIV></DIV></DIV><br />
<DIV class=Para>In general, one would like to choose the integration time <SPAN class=EmphasisTypeItalic>τ</SPAN> <SUB><SPAN class=EmphasisTypeItalic>i</SPAN> </SUB>as short as possible and the coherence time <SPAN class=EmphasisTypeItalic>τ</SPAN> <SUB><SPAN class=EmphasisTypeItalic>coh</SPAN> </SUB>as long as possible. The coherence time is inversely related to the spectral resolution of the spectrometer which in turn relates linearly to the maximum depth range of the system. In conclusion, the parameter that most determines the system performance is the readout and dark noise of the detector <SPAN class=EmphasisTypeItalic>σ</SPAN> <SUB><SPAN class=EmphasisTypeItalic>rd</SPAN> </SUB>.</DIV><br />
<DIV></DIV><br />
<DIV id=Sec4 class=]()




5.1.3 Autocorrelation Noise: Dynamic Range and Digitization Depth
SD-OCT is based on spectral interferometry, where recombined light from reference and sample arms is spectrally separated, detected, and converted into a depth profile. The detected interference signal at the spectrometer may be expressed as [4]
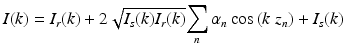
where I r (k) and I s (k) are the wavelength-dependent intensities reflected from reference and sample arms, respectively, and k is the wave number. The second term on the right-hand side of Eq. 5.6 represents the interference between light returning from reference and sample arms. α n is the square root of the sample reflectivity at depth z n . Depth information is retrieved by performing an inverse Fourier transform of Eq. 5.6, yielding the following convolution [4]:
![$$ {\left|F{T}^{-1}\left[I(k)\right]\right|}^2={\Gamma}^2(z)\otimes \left\{\delta (0)+{\displaystyle \sum_n{\alpha}_n^2\delta \left(z-{z}_n\right)+}{\displaystyle \sum_n{\alpha}_n^2\delta \left(z+{z}_n\right)+\kern0.5em }O\left[{I}_s^2/{I}_r^2\right]\right\}, $$](/wp-content/uploads/2017/03/A76297_2_En_6_Chapter_Equ7.gif)
with Γ(z) representing the envelope of the coherence function. The first term in the braces on the right-hand side describes the autocorrelation signal from the reference arm and has magnitude unity. The second and third terms are due to interference between light returning from reference and sample arms and form two images, where each has magnitude on the order of I s /I r . These two terms provide mirror images, where one is retained. The final term, with magnitude on the order of I s 2/I r 2, describes autocorrelation noise due to interference within the sample arm [4, 9]. I s and I r represent the total intensity reflected from sample and reference arms, respectively. Equation 5.7 indicates that the relative contribution of sample autocorrelation noise can be reduced by increasing the reference arm power with respect to the signal. Decreasing the detector integration time permits an increase in the reference arm power without saturating the detector, decreasing the ratio I s 2/I r 2 and consequently reducing the contribution of autocorrelation noise in ultrahigh-speed SD-OCT.
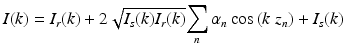
(5.6)
![$$ {\left|F{T}^{-1}\left[I(k)\right]\right|}^2={\Gamma}^2(z)\otimes \left\{\delta (0)+{\displaystyle \sum_n{\alpha}_n^2\delta \left(z-{z}_n\right)+}{\displaystyle \sum_n{\alpha}_n^2\delta \left(z+{z}_n\right)+\kern0.5em }O\left[{I}_s^2/{I}_r^2\right]\right\}, $$](/wp-content/uploads/2017/03/A76297_2_En_6_Chapter_Equ7.gif)
(5.7)
In the shot noise limit, the signal-to-noise ratio (SNR) in the spectral domain system has been shown to be [7]
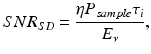
where η is the spectrometer efficiency, P sample is the sample arm power returning to the detection arm, τ i is the detector integration time, and E v is the photon energy. Unlike the SNR in the time domain, Eq. 5.8 demonstrates that in the shot noise limit, SNR SD is independent of the spectral width of the source. This implies that the axial resolution can be increased at no penalty to the SNR, provided that the full spectral width of the source can be imaged onto an array detector. However, this result should be interpreted with some care. The sample arm power returning to the detection arm is assumed to come from a single reflecting surface. In tissue, however, the reflected power comes from multiple structures along a depth profile. The SNR for a particular position along the depth profile is given on average by the total power reflected by all structures within the coherence length of the source. As the resolution increases (the coherence length decreases), the total reflected power within the coherence length decreases. As a consequence, the SNR at a particular position along the depth profile will reduce as the resolution increases by increasing the source optical bandwidth.
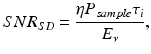
(5.8)
5.1.4 Bit Resolution and Well Depth of the CCD, Dynamic Range, and Sensitivity
Earlier SD-OCT system designs emphasized the necessity of large well depth (number of electrons that could be stored in a single element of the CCD) and large bit depth as an important consideration to realize the high sensitivity and dynamic range that can be achieved by OCT. Sensitivity is the ratio of maximum signal over noise floor, where the maximum signal is defined by placing a perfect reflector in the sample arm. The dynamic range of a system is the maximum signal over the noise floor that a particular system can measure without, e.g., saturating a detector, overloading an amplifier, or exceeding a digitization range. In practice, no TD- or SD-OCT system realizes a dynamic range equal to the sensitivity, which can easily be over 100 dB. In general, this is not necessary, since tissue reflectivity is at least four orders of magnitude smaller than a perfect reflector. A system dynamic range of 40–60 dB suffices in most cases.
A 60-dB dynamic range in a TD-OCT system would require at least a 10-bit A/D range (6 dB per bit) digitizing the interference modulation on the DC background. An advantage of TD-OCT systems is that the signal can be high-pass filtered to remove the DC component and only pass the interference modulation to the digitization circuitry. In SD-OCT, the CCD detectors do not easily permit removal of a DC component, and considerations similar to that for a TD-OCT system suggest that for an SD-OCT system the A/D range needed to capture the interference modulation on top of the DC background with sufficient resolution to provide 40–60-dB dynamic range would require an A/D resolution significantly exceeding that of a TD-OCT system. Fortunately, the required bit resolution capturing the interference modulation to achieve 40–60-dB dynamic range turns out to be much smaller.
In SD-OCT the reflectivity in z-space is given by the square of the Fourier component in k-space (Eq. 5.7). The resolution of the Fourier component is proportional to the resolution of the modulation depth of the spectrum, multiplied with the number of illuminated pixels of the camera (on the order of ∼1,000). Thus, a relative small resolution of the modulation depth of the spectrum (on the order of a few bits) gets amplified by the number of illuminated pixels, easily providing a dynamic range in z-space exceeding 40–60 dB. The presence of multiple reflecting structures complicates matters. For example, two strong reflectors in the sample arm each create a periodic modulation of the spectrum. These modulations are summed and create a larger modulation depth of the spectrum on the DC background that should be captured without saturation of the CCD or clipping of the digitization circuitry. Therefore, the calculation of the dynamic range of an SD-OCT system is not a straightforward calculation of the strongest single reflector that can be measured, but depends on the total power reflected by the sample. As the total reflected power increases, the dynamic range with which the reflectivity of a particular location can be measured decreases.
5.1.5 Experimental Demonstration of SNR Advantage
A number of groups have presented empirical evidence demonstrating the SNR advantage of SD-OCT over time domain OCT. The following section describes a direct comparison between a TD-OCT and an SD-OCT system [10]. To compare directly the SNR performance of TD- and SD-OCT, a weak reflector was placed in the sample arm of our system (Fig. 5.1).
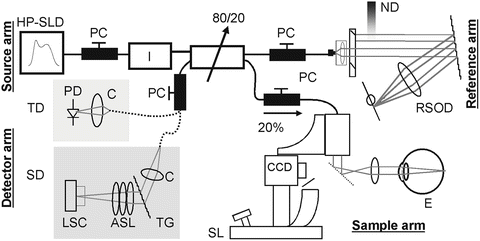

Fig. 5.1
Time and spectral domain system integrated into a single instrument for a direct comparison of the SNR (Reproduced from Ref. [10] with permission from the Optical Society of America)
The power reflected by the weak reflector measured at the fiber tip in the detection arm was 1.3 nW. The polarization states of sample and reference arm light were carefully aligned to maximize interference. First, 256 depth profiles at a speed of 4 ms per depth profile were acquired with our TD-OCT system, scanning over a depth of 1.4 mm in air. The signal pass bandwidth (BW) was 100 kHz. Then the detection arm was connected to the spectrometer, and 256 spectra were acquired at a speed of 100 μs per spectrum. To reduce fixed pattern noise in the SD-OCT measurement [6], each individual spectrum was divided by the average spectrum of 1,000 reference arm spectra. The resulting spectrum was multiplied by a Gaussian to reshape the spectrum [25]. A Fourier transform links z- and k-space. Because of the nonlinear relation between k and λ, the spectra were interpolated to create evenly spaced samples in the k domain [9] before Fourier transformation of the spectra to generate depth profiles.
Figure 5.2 shows the averaged depth profiles acquired with the respective configurations, demonstrating an SNR of 44.3 and 50 dB for TD- and SD-OCT, respectively. Both depth profiles were normalized on the reflectivity peak. The TD measurement was shifted such that the peaks coincide. Some fixed pattern noise was still present in the SD-OCT measurement, resulting in peaks at 84 and 126 μm. Since the SD-OCT system was 5.7 dB more sensitive, operated at a speed 40 times faster (corresponding to 16 dB) than the TD-OCT system, the combined sensitivity improvement was 21.7 dB or a factor of 148. The theoretical shot noise limited SNR in TD and SD is given by, respectively [6, 7],
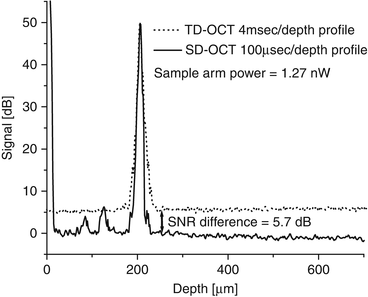
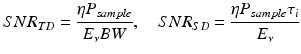
resulting in 46.7 dB (TD) and 51.9 dB (SD), where η = 0.85 was used for a PIN diode in TD. The measured TD and SD SNRs were, respectively, 2.4 and 1.9 dB less than the theoretical optimal performance, where 1 dB in TD was determined to be due to thermal noise contributing to the total noise. The measured coherence function FWHM in air was 6.3 μm in both TD and SD.

Fig. 5.2
Direct comparison of the SNR between SD- and TD-OCT (Reproduced from Ref. [10] with permission from the Optical Society of America)
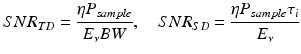
(5.9)
5.1.6 Shot Noise Limited Detection
The different noise components present in the system were measured and analyzed to demonstrate that performance was shot noise limited. The readout and shot noise at a 29.3 kHz readout rate are shown in Fig. 5.3.


Fig. 5.3
Noise components in the detector. The shot noise level was determined with illumination of the reference arm only and was used to determine the A/D resolution of the detector. The theoretical shot noise curve was fit using Eq. 5.10 to the measured noise, giving a Δe of 173 electrons and a corresponding well depth of 177,000 electrons (Reproduced from Ref. [11] with permission from the Optical Society of America)
The noise was determined by calculating the variance at each camera pixel for 1,000 consecutive spectra. Dark noise measurements were taken with the source light off. Only light returning from the reference arm was used to measure the shot noise in the system. The shot noise expressed in number of electrons is (I PV (λ)Δe)1/2, where I PV (λ) is the pixel value corresponding to the intensity at each CCD element, with values ranging from 0 to 1,024 (10 bits), and Δe is the analog-to-digital conversion resolution, which corresponds to the number of electrons required for an incremental increase of 1 pixel value. Thus, the variance as measured in pixel values is defined as
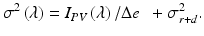
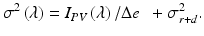
(5.10)
The first term on the right-hand side of Eq. 5.10 is the shot noise contribution and the second term is the readout contribution to the total noise. The CCD well depth was determined by fitting the theoretical expression for shot noise to the measured shot noise, using Δe as the fitting parameter, and limiting the fit to the central 700 pixels. From this measurement, Δe was calculated to be 173 electrons. Assuming that the maximum pixel value corresponds to the full well depth, a well depth of 177,000 electrons was calculated, in agreement with our previously published result [10]. Shot noise dominated readout and dark noise when the intensity reached 6 % of the saturation value. Relative intensity noise (RIN) is never dominant in this setup, since the maximum power per pixel (4.6 nW) at a 34.1 μs integration time does not meet the criteria for RIN-dominated noise [10].
5.1.7 Remapping to k-Space, Sensitivity Drop-Off as a Function of Depth, Spectrometer Resolution, Fixed Pattern Noise Removal
In SD-OCT, the structural information, i.e., the depth profile (A-line), is obtained by Fourier transforming the optical spectrum of the interference as measured by a spectrometer at the output of a Michelson interferometer [3, 9]. Fourier transformation relates the physical distance (z) with the wave number (k = 2π/λ). The spectra obtained with SD-OCT are not necessarily evenly spaced in k-space. A proper depth profile can be obtained only after preprocessing to obtain data that is evenly spaced in k-space [9], and this requires accurate assessment of the wavelength corresponding to each spectral element.
Determination of this wavelength mapping is typically performed using separate measurements of a reflective surface at different positions in the sample arm [9, 26]. The importance of proper wavelength assignment for SD-OCT was first noted by Wojtkowski et al. [9]. Incorrect wavelength mapping generates a depth-dependent broadening of the coherence peak similar in appearance to dispersion in structural OCT images. The disadvantage of such calibration methods is that they typically require separate measurements of a reflective surface. Using the example of a clinical ophthalmic system, calibration data from a model eye are acquired before or after imaging of the patient in order to later determine the appropriate wavelength mapping. The calibration procedure may be necessary for each measurement session due to thermal and mechanical instabilities of the spectrometer, which is not practical in a clinical setting. Recently we proposed an autocalibration technique wherein the calibration data does not have to be acquired separately, but is contained within the data of interest [27].
Proper wavelength assignment can be achieved by imposing onto the spectrum a known modulation that can be used for calibration. In the system presented here, we introduce a perfect sinusoidal modulation as a function of k by passing the light through a microscope cover slip in the interferometer’s source arm. This slide creates spectral modulation by combining the light that passes directly through the glass with the light that is internally reflected twice before transmission. The interference can be characterized by an optical path mismatch of 2dn, where n is the refractive index and d is the thickness of the glass cover slip, and is of the form cos(2dnk). This spectral modulation is a perfect cosine as a function of k, assuming that n is independent of the wavelength for the bandwidth of the light source.
The presence of this spectral modulation is key in assigning the correct wavelength to each pixel of the CCD in the spectrometer case. In general, the pixels do not correspond to evenly distributed k, and therefore, the detected intensity modulation is not a perfect sinusoid. The autocalibration technique alters the wavelength assignments until the resulting spectral modulation matches a perfect sinusoid as a function of k. This sinusoidal intensity modulation produces in all A-lines an identical strong peak along z corresponding to the optical thickness of the slide. This peak can be easily removed as fixed pattern noise from the structural intensity images in a patient scan.
Figure 5.4a shows a typical intensity modulation generated by the slide for the spectrum of a Ti:sapphire laser (INTEGRAL OCT, FEMTOLASERS, Austria) with a spectral bandwidth of 150 nm centered at 800 nm. This spectrum has been obtained from a patient scan by taking the mean of 1,000 spectra corresponding to one OCT image. The interference fringes resulting from the retinal structure are washed out in this mean, while the fringes from the slide in the source arm are unaffected since they are the same in each spectrum. The spectral interference fringes from the slide are isolated with a band-pass filter in Fourier space, and the result is shown in Fig. 5.4b in the CCD pixel space. By keeping only the peak from the slide, we also remove the DC component of the spectral interference, illustrated in Fig. 5.4b as a zero-mean interferogram. When represented as a function of k, the fringes in Fig. 5.4b should be perfectly periodic. For a perfect sinusoid, the phase, or the argument of the sinusoidal oscillation, is linearly related to k. This condition is used to determine the accuracy of the wavelength assignment; an improper wavelength assignment results in phase nonlinearity as a function of k. The wavelength mapping is determined by minimizing the nonlinearity of this phase. An initial estimate of the wavelength array W is generated using the grating equation based on the geometrical design of the spectrometer [26] or, alternatively, with a third-order polynomial bringing the generated wavelengths in the spectral range of the light source. W is used to interpolate the spectral interference fringes to equally spaced k values. The quality of this interpolation process is improved by zero padding the spectrum. The next step is to iteratively determine and apply corrections to the wavelength assignment by reducing the phase nonlinearity. The phase of the zero-padded and k-space interpolated spectrum is determined and fit with a third-order polynomial. The nonlinear part σ(k) of the polynomial fit (which only has the quadratic and cubic dependence on k and represents the deviation from a perfect linear phase) is used for correcting the wavelengths W based on the assumption that this nonlinearity is generated by wrong wavelength assignment.
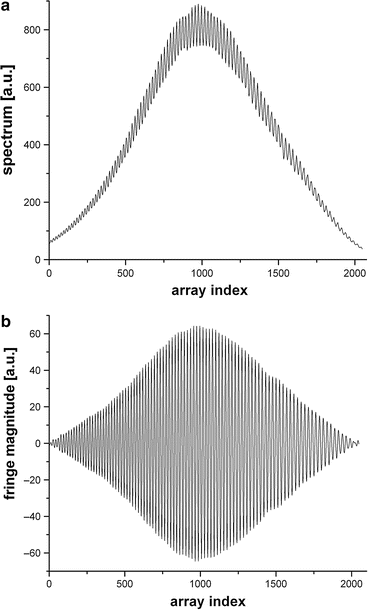

Fig. 5.4
(a) Spectrum (in arbitrary units) of interference generated by the slide as a function of the index of the CCD pixels. The spectrum was obtained by averaging 1,000 spectra from a retinal scan of a patient. Since the retinal structural information changes in each consecutive spectrum, but the spectral modulation by the glass cover slip is constant, only the spectral modulation by the cover slip is retained after averaging 1,000 spectra. (b) Spectral interference fringes (in arbitrary units) corresponding to the slide, shown in CCD pixel space (Reproduced from Ref. [27] with permission from SPIE)
Therefore, we calculate a new k-array k′, starting from the previous k = 2π/W array and σ(k), using the equation k′ = k + σ(k)/z peak , where z peak is given by z peak = 2πPeak _ Index/(k max − k min). Peak_Index is the location of the coherence peak corresponding to the slide in index space, and kmax and k min are the extremes of k. This correction is applied iteratively to the original spectral interference, and the final result is the wavelength array W′ = 2π/k′ that corresponds to basically linear phase as a function of k′. The condition to be met in order to exit the loop could be either a maximum number of iterations or a tolerance in the change of the wavelength array after each iteration. The wavelength array W′ can now be used to map the spectrometer data to the correct k values for processing the data into depth profiles.
5.1.8 Dispersion Compensation
One difficulty that arises from using ultra-broadband sources in a fiber-based OCT setup is chromatic dispersion in optically dense materials like glass, tissue, and water. The speed of light depends on the refractive index n(k) of the material, slowing down certain spectral components to a greater extent than others, hence dispersing the light. The total amount of dispersion increases linearly with length of the dispersive medium as well. Chromatic dispersion in air is negligible. Considerable amounts of dispersion can be tolerated if the dispersion in the two arms of the interferometer is equal, thus creating a coherence function that will be free of dispersion artifacts. However, when sample and reference arms contain different lengths of optical fiber or other dispersive media, a dispersion mismatch occurs. In the sample arm, the introduction of an eye with unknown axial length creates a similar effect. The coherence function will not only be broadened by unbalanced dispersion, but its peak intensity will decrease as well [28]. Second-order or group-velocity dispersion can be compensated for by changing the lens to grating distance in a rapid-scanning optical delay line [29]. However, this method does not compensate for higher orders of dispersion. Alternatively, one can balance dispersion in an OCT system by inserting variable-thickness BK7 and fused silica prisms in the reference arm [30]. The previously mentioned unknown factor introduced by an eye with unknown axial length requires a flexible method for dispersion compensation. An alternative to compensation in hardware is dispersion compensation in software. De Boer et al. induced dispersion in the delay line of a TD-OCT system equipped with an optical amplifier-based source (AFC technologies, λ0 = 1,310 nm, Δλ = 75 nm) and compensated for dispersion artifacts in structural intensity images obtained in an onion [31]. Fercher et al. compensated for dispersion induced by a glass sample [32, 33]. Other dispersion compensation algorithms are described by Marks et al. [34, 35]. Below we will give an example of compensation in software for dispersion induced by an ultra-broadband source and remove artifacts from retina data [12]. A nearly identical approach was virtually simultaneously published [13].
A dispersion mismatch introduces a phase shift e iθ(k) in the complex cross-spectral density I(k) as a function of wave vector. Since spectrometer data is acquired as a function of wavelength, data has to be transformed to k-space first as detailed above. The relation between the phase θ(k) and the multiple orders of dispersion can best be described by a Taylor series expansion:
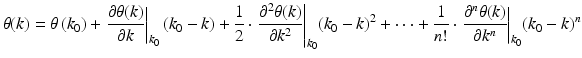
with λ 0 the center wavelength and k 0 equal to 2π/λ 0. The first two terms describe a constant offset and group velocity, respectively, and are not related to dispersive broadening. The third term represents second-order or group-velocity dispersion. Dispersion mismatch in sample and reference arms is largely compensated by this term, although adjustment of higher-order dispersion can be necessary as well, especially when an ultra-broadband source is used. Dispersion can be removed by multiplying the dispersed cross-spectral density function I(k) with a phase term e −iθ(k) .
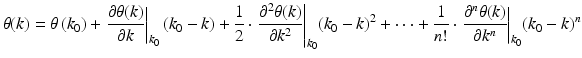
(5.11)
We will illustrate a method to obtain the phase term e −iθ(k) . To determine this phase term for dispersion compensation of data obtained in the human eye in vivo requires a coherence function obtained from a well-reflecting reference point in the eye. We found that it is possible to use the center of the fovea (foveal umbo) for this purpose because this part of the eye acts as a good reflector [12]. To determine the phase term, after linear interpolation to k-space, the spectrum is Fourier transformed to z-space, where it is shifted such that the coherence function is centered on the origin. A complex spectrum in k-space is obtained after an inverse Fourier transformation. The phase term θ(k) is equal to the arctangent of the imaginary component divided by the real component and indicates how much subsequent wave numbers k are out of phase with each other. This function was fit to a polynomial expression of the 9th order, yielding a set of coefficients α 1–9. Individual spectra obtained from a volunteer were first multiplied with a phase e −iθ(k) as determined from the last seven polynomial coefficients and then inversely Fourier transformed into A-lines, thus removing dispersion.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


