Fig. 48.1
Low-coherence Michelson interferometer
A low coherent light source, e.g., an SLD, emits a light beam with short coherence length towards the Michelson interferometer, where it is first split by a beam splitter. The split field travels in a reference path, reflecting from a reference mirror, and also in a sample path where it is reflected from multiple layers within a sample. Due to the broadband nature of the light, interference between the optical fields is only observed when the reference and sample arm optical lengths are matched to within the coherence length of the light. Therefore, the depth (axial) resolution of an OCT system is determined by the temporal coherence of the light source. Sharp refractive index variations between layers in the sample medium manifest themselves as corresponding peaks in the interference pattern.
To describe OCT mathematically, it is useful to express the electric field E(ω, t) as a complex exponential.
![$$ E\left(\omega, t\right)=s\left(\omega \right) \exp \left[-i\left(\omega t+kz\right)\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_49_Chapter_Equ1.gif)
![$$ E\left(\omega, t\right)=s\left(\omega \right) \exp \left[-i\left(\omega t+kz\right)\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_49_Chapter_Equ1.gif)
(48.1)
This is a plane-polarized solution to the wave equation, with source field amplitude spectrum s(ω), frequency ω, and time variation t. The second term in the exponential, in terms of wave number k and distance z, simply accounts for phase accumulated throughout the interferometer. Since the input phase is arbitrary and the interferometer only measures the relative output phase between the two optical paths, the phase term can be dropped from the input electric field. The field in each part of the interferometer is denoted by subscripts as follows: E out, E r, and E s corresponding to the input, output, and reference and sample arm optical fields, respectively. The sample has a frequency-domain response function H(ω) that describes its internal structure and accounts for phase accumulation therein. Optical detectors are square law intensity detection devices, where the recorded intensity is proportional to a time average over the electric field multiplied by its complex conjugate. Assume that the interferometer operates in air, then the output from the detector is
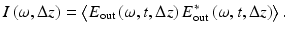
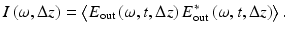
(48.2)
The angled brackets denote a time average, given by


(48.3)
It can be shown that the intensity is a sum of three terms
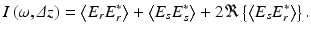
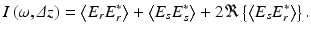
(48.4)
Here, Δz = Δtc/n air is the mismatch distance between the reference and sample arm. The first two terms can be identified as “self-interference” that is not relevant to the OCT imaging and therefore is dropped in the following treatment. The last term is the real part (denoted by ℜ) of the complex “cross-interference” that is the interest of concern. Making the relevant mathematical operations and substituting for the field spectrum s(ω) a corresponding intensity spectrum S(ω) = ∣s(ω)∣2, the frequency and path difference-dependent intensity is given by
![$$ I\left(\omega, \Delta z\right)=\Re \left\{S\left(\omega \right)H\left(\omega \right) \exp \left[-i\phi \left(\Delta z\right)\right]\right\} $$](/wp-content/uploads/2017/03/A76297_2_En_49_Chapter_Equ5.gif)
where ϕ(Δz) is the phase accumulated in translating the reference mirror by a geometric distance Δz, ϕ(Δz) = 2ωn airΔz/c. The sample response function H(ω) describes the overall reflection from all structures distributed in the z direction within the sample and is given by
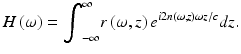
![$$ I\left(\omega, \Delta z\right)=\Re \left\{S\left(\omega \right)H\left(\omega \right) \exp \left[-i\phi \left(\Delta z\right)\right]\right\} $$](/wp-content/uploads/2017/03/A76297_2_En_49_Chapter_Equ5.gif)
(48.5)
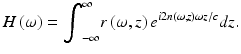
(48.6)
The function n(ω, z) is the frequency-dependent, depth-varying group refractive index and r(ω, z) is a function of the reflected photons escaped from the sample at depth z that bears the structure features of the sample. The exponential term accounts for phase accumulated by the multiple optical paths within the sample.
From Eq. 48.6 it is evident that information about the optical structure of the sample can be obtained from measurements in both the time and frequency domains. Clearly the imaging depth and contrast are related to the function r(ω,z). Assuming that the sample is transparent consisting of N multiple layers that do not absorb and scatter the incoming light, r(ω, z) can be simplified as the reflectivity of each layer, r j (j = 1,2,…, N), that can be determined by the application of Fresnel’s equations:


(48.7)
Thus, for such a simple multilayered sample, the sample response function can be modeled as a summation over N individual layers and assuming negligible dispersion [9]
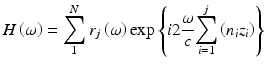
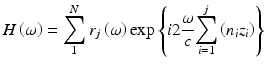
(48.8)
Here, z i is the thickness of the ith layer with a group refractive index n i . However, it will never be the case for the biological tissues where there are almost no planar boundaries, i.e., the interfaces distinguished by the refractive index. And more important, there are other optical properties of tissue that are detrimental to the OCT imaging of microstructures inside the tissue. The most notable optical properties that are responsible for degrading the imaging depth and contrast are the absorption and scattering. It is reasonable to consider that biological tissue has depth-varying distribution of absorption and scattering. Thus, the sample response function will be modulated by the local optical properties. For the case of only one scatter within the coherence volume, the sample response function from this particular scatter at the depth z can be expressed as the multiplication of backscattering profile r b (ω, z) and the accumulated attenuation r a (ω, z) along the optical path in the sample before that scatter, such that
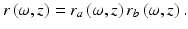
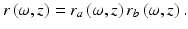
(48.9)
The accumulated attenuation r a (ω, z) along the optical path has both scattering and absorption contributions. In simple cases, it follows Beer’s law:
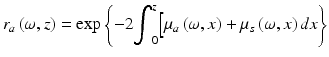
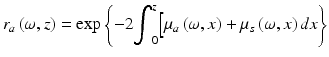
(48.10)
Here, μ a (ω, z) and μ s (ω, z) are wavelength dependent and spatially varying absorption and scattering coefficients of the biological sample, respectively. The backscattering coefficient at depth z, r b (ω, z) is determined by the local refractive index variation that gives the imaging contrast of the final OCT image. Therefore, the sample response function at depth z can now be expressed by
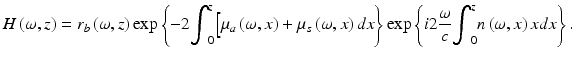
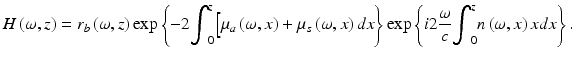
(48.11)
Thus, the explanation of OCT imaging contrast and depth can be decoupled from the above equation, where the imaging contrast is provided by the local backscattering coefficient, r b (ω, z), and the imaging depth is determined by the attenuation coefficient of the targeted sample. In particular, the imaging contrast at a certain depth z is severely affected by the accumulated light attenuation before the depth z. That is to say, if there is no attenuation of light before the depth z, theoretically the imaging depth z can approach infinity while the imaging contrast is provided by the true local reflectivity of the sample. However, as we are dealing with the biological tissue which is highly scattering in nature, the imaging depth would be determined by the point at which the light is attenuated to the limit of the system noise floor. Thus, the weaker the light attenuation before the depth z, the higher the imaging contrast at the depth z and the further the light can reach beyond z.
48.2.2 Light Scattering in Tissue
As explained in the previous section, the OCT imaging depth and contrast are affected by the total spectral-dependent attenuation coefficient of the sample. That is to say, the depth of penetration for the light into a biological tissue depends on the scattering characteristics and absorptivity of the tissue. To simplify the discussion, here we assume that the absorption and scattering coefficient of the sample are not wavelength dependent. Further, as the OCT imaging is usually performed in the near-infrared region of spectrum, compared to the scattering effect the absorption is relatively small and is therefore not discussed in the following sections. However, this is by no means to say that the absorption is not a factor in influencing OCT imaging performance. Please refer to the other chapters in this book, particularly the spectroscopic OCT, for details of exciting usage of OCT to sense the absorption in tissue, thereby the molecular-sensitive detection.
Optically, tissue can be described as a spatial distribution of refractive index on the microscopic scale that could be classified into those of the extracellular and intracellular components [63–65]. The local refractive index within the tissue can vary from anywhere within the background refractive index, i.e., 1.34 and 1.50 depending on what type of soft tissue is concerned. It is this variation of refractive index distribution within the tissue that causes a strong light scattering. Figure 48.2 shows a hypothetical index profile formed by measuring the refractive index along a line in an arbitrary direction through a volume of tissue and corresponding to the statistical mean index profile. The widths of the peaks in the actual index profile are proportional to the diameters of the elements, and their heights depend on the refractive index of each element relative to that of its surroundings. This is the origin of the tissue-discrete particle model. In accordance with this model, the index variations may be represented by a statistically equivalent volume of discrete particles having the same index but different sizes.
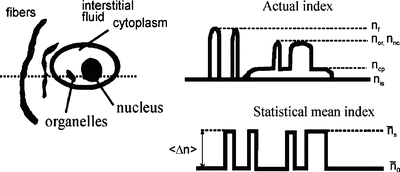

Fig. 48.2
Spatial variations of the refractive index of a soft tissue. A hypothetical index profile through several tissue components is shown, along with the profile through a statistically equivalent volume of homogeneous particles. The indices of refraction labeling of the profile are defined in the text [63, 66]
To describe theoretically the optical scattering in tissues, attempts have been made using the particle model with some success [63, 64]. Based on the model, the biological tissue is treated as that consisting of the discrete scattering centers with different sizes randomly distributed in the background media. According to the Rayleigh-Gans approximation, the reduced scattering, μ s ′ = μ s(1 − g), of turbid media is related to the reduced cross section, σ s ′, and the total number of scattering particles per unit volume, i.e., number density, ρ:
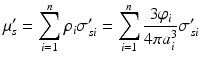
and
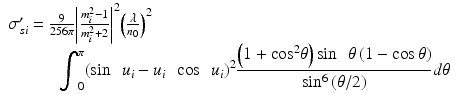
where u i = 2(2πa i n 0/λ)sin(θ/2), m i = n si /n 0 with n si and n 0 being the refractive indices of the ith scattering centers and background medium, φ i the volume fraction of the ith particles, and a i the radius of the ith scatterer. This equation is valid for non-interacting Mie scatterers, g > 0.9, 5 < 2πa/λ < 50, and 1 < m < 1.1.
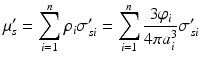
(48.12)
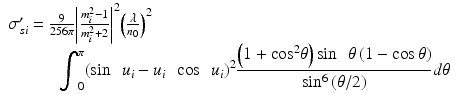
(48.13)
It can be seen that the reduced scattering coefficient of the scattering medium is dependent on both the refractive index ratio, m i , and the size of the scattering centers. A study by Schmitt and Kumar [66] reveals that the spectrum of index variation exhibits a power law behavior for spatial frequencies from 0.5 to 5 μm–1. In other words, they found evidence for a broad distribution of scatters in tissue cells with sizes ranging from 0.2 to 2 μm. Studies by Beauvoit et al. [40] and Mourant et al. [67] revealed that the size of scattering centers varies in radius from less than 0.2 μm to more than 1 μm. Thus, the particles inside the tissue with sizes in microscopic scale are mainly responsible for the light scattering.
The refractive indices of tissue structure elements, such as fibrils, interstitial medium, nuclei, cytoplasm, organelles, and the tissue itself can be derived using the law of Gladstone and Dale, which states that the resulting value represents an average of the refractive indices of the components related to their volume fractions
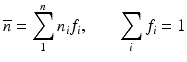
where n i and f i are the refractive index and volume fraction of the individual components, respectively, and N is the number of components. The statistical mean index profile in Fig. 48.1 illustrates the nature of the approximation implied by this model. According to Eq. 48.13, the average background index is defined as the weighted average of the refractive indices of the cytoplasm and the interstitial fluid, n cp and n is , as
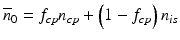
where f cp is the volume fraction of the fluid in the tissue contained inside the cells. For the human soft tissues, the total fluid occupies approximately 60 % of the body weight, of which 40 % is the intracellular component and 20 % the extracellular component. As a result, approximately 70 % of the total fluid in the soft tissue is contained in the intracellular compartment and 30 % in the extracellular compartment. Estimated from the dissolved fractions of proteins and carbohydrates in the intracellular and extracellular fluids, refractive indices of the extracellular fluid, ne, and the intracellular fluid, ni, are found to be approximately 1.34 and 1.36, respectively [6]. The average background refractive index of a soft tissue can thus be estimated from the weighted refractive indices of ne and ni as
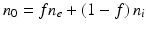
where f is the fraction of the fluid in tissue contained in between the cells. Therefore, it follows from Eq. 48.15 that n 0 = 0.3 × 1.34 + 0.7 × 1.36 = 1.354.
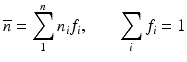
(48.13)
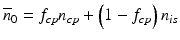
(48.14)
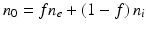
(48.15)
Figure 48.3 illustrates the reduced scattering coefficient of the turbid medium, predicted by the Rayleigh-Gans approximation, against the refractive index of background medium for the wavelengths at 800 nm and 1,300 nm, respectively. The parameters taken for scattering centers in the numerical evaluation were the refractive index n s = 1.46, the volume fraction φ = 0.3, and the radius a = 1 μm. It is clear from Fig. 48.3 that the reduced scattering of the tissue is dramatically reduced with the increase of refractive index of the background medium. The reduction rate is approximately the same for both the wavelength applied, with 800 nm being a little bit faster than that of 1,300 nm. At least threefold reduction is expected if the refractive index of the background medium is changed from n 0 = 1.354 to n 0 = 1.4.


Fig. 48.3
Reduced scattering coefficient calculated from Rayleigh-Gans approximation as a function of the refractive index of the background medium for the wavelength at 800 and 1,300 nm, respectively. Please see the text for the parameters used in the numerical evaluation [54]
It is possible to achieve a marked impairment of scattering by means of the intra-tissue administration of appropriate chemical agents. Conspicuous experimental optical clearing in human and animal sclera; human, animal, and artificial skin; human gastrointestinal tissues; and human and animal cartilage and tendon in the visible and NIR wavelength ranges induced by the administration of x-ray contrast agents (Verografin, Trazograph, and Hypaque-60), glucose, propylene glycol, polypropylene glycol-based polymers (PPG), polyethylene glycol (PEG), PEG-based polymers, glycerol, and other solutions as has been described in Refs. [27, 34–62].
With the connection from the last section, such effect of reduction of scattering in biological tissue can be explored in the OCT to enhance its imaging performance, aspects which will be discussed in the following sections.
48.3 Monte Carlo Simulations
To illustrate how the multiple scattering has the effect on the OCT imaging performance, recently, Wang [32] used the Monte Carlo simulation technique (refer to ref [68] for details of Monte Carlo techniques) to systematically simulate such effects with an emphasis on the effects on imaging depth, resolution degradation, and signal localization. Generally from the results, it was found that signal localization and attenuation are dependent on the optical properties of tissue. The high scattering coefficient and the low degree of forward scattering are the primary causes for the degradation of signal localization and attenuation, leading to complication of interpretation of the measured OCT signals. More importantly, it was found that the imaging resolution is a function of the probing depth within the medium, as opposed to the claimed OCT system resolution. This fact has been overlooked recently in the OCT imaging applications. The imaging resolution is greatly reduced with increasing depth; this case is even more severe for the highly scattering medium. Therefore, attention must be paid to this fact when applying the OCT to human organs because of the high scattering nature of tissue.
Let us revisit the OCT system by looking closely at the backscattering light from the high scattering medium that has the possibility to contribute to the interference signal. A simple schematic of OCT system when probing the highly scattering medium is illustrated in Fig. 48.4, where the sample beam progressively loses its spatial coherence as it penetrates a turbid biological tissue. This loss of coherence results from the scattering by a variety of cellular structures with sizes ranging from less than one wavelength (e.g., cellular organelles) to several hundreds of micrometers (e.g., the length of a collagen fiber). As illustrated in Fig. 48.4, the dominant scattering interaction of the probing beam in the turbid medium can be categorized into three types [32, 69]: single backscatter a, small-angle forward scatter b, and extinction by absorption or wide-angle scatter c (i.e., light scattered out of the view of the interferometric receiver). The detector will only receive the first two categories of scatters because of the heterodyne detection characteristics of the OCT system. Furthermore, the low-coherence light source used, as stated in Sect. 12.2, provides a time gate to enable the detector to receive only those photons that traveled beneath the tissue surface with their optical path lengths matching the optical path length of the reference arm to within coherence length of the light source. Consequently, the OCT system in reality plays a role to sieve all the backscattering photons that emerged at the detector according to their arrival times or equivalently the optical path lengths that the photons have traveled. Therefore, to enable the detector to produce the signal, the following criteria must be fulfilled:
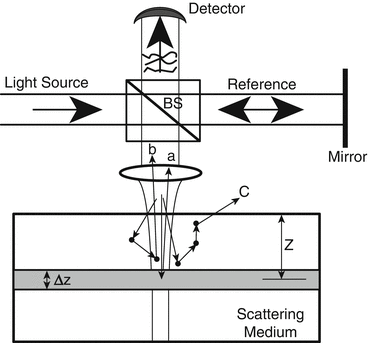
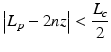
where L p is the optical path length that the photon has traveled within the tissue, n is the refractive index of the medium, and z is the depth of a layer whose distance from the tissue surface matches the scanning distance of the mirror, nz, in the reference arm. For signal localization, we normally expect that the detected photons would be backscattered from the layer whose thickness is determined by


Fig. 48.4
Simple schematic of OCT system showing scattering interactions between a probing beam and biological tissue. Three types of interactions are backscattered from within the tissue: single scatter a, small-angle scatter b, and wide-angle scatter c. A layer with a thickness Δz at the depth of z is the expected layer for OCT localization
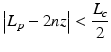
(48.16)

(48.17)
However, because of the multiple scattering, there are possibilities for those photons contributing to the detected signal that are not backscattered from the expected layer, z, but fulfill the criteria of Eq. 48.17. As a consequence, these photons degrade the signal attenuation, localization, and resolution because they are not from the desired layer, leading to a signal artifact complicating the interpretation of the OCT image. The author in the paper [32] termed the photons that satisfy Eq. 48.17 as the least-scattered photons (LSP) and otherwise as the multiple-scattered photons (MSP). It is clear that the MSP comes solely from the interaction type b, while the LSP includes the interaction type a and part of type b because the photons backscattered from the desired layer might be subject to multiple scattering but with very small angle scattering. A distinct advantage of MC simulation technique is its ability to sort the LSP and MSP according to their optical path lengths, thereby enabling the investigation of their influence on the OCT signal attenuation and localization. Signal localization can be investigated systematically by means of the point spread function (PSF) at the specific depth for different optical properties to illustrate how the LSP and MSP contribute to signal localization.
With these conventions in mind, we now turn to looking at some results of how multiple scattering affects the OCT imaging performances by the use of the Monte Carlo simulation technique. For details, refer to the reference [32].
Figure 48.5 gives typical examples of depth point spread function (zPSF) at different probing depths for the turbid media representing moderate scattering in the left column (μ s = 10 mm–1) and highly scattering in the right (μ s = 67 mm–1). The figures were obtained for g = 0.7, 0.9, and 0.98 from top to bottom, respectively, to allow us to scrutinize the influence of the anisotropic parameter of the medium on the signal localization. The depths monitored are indicated in each figure. The filled symbol curves are the actual PSFs that are the summation of LSP and MSP signals from a specific depth. However, to investigate the effects of LSP and MSP signals separately on the PSFs, the signals from the LSP alone are plotted in each case, represented by the hollow symbol curves. Firstly, it is obvious that the worst case is from the medium with the highest scattering coefficient and lowest degree of forward scattering, i.e., μs = 67 mm–1 and g = 0.7 in this case (see the top right figure), where signal localization is merely discerned at a depth of 50 μm. Even at this depth, the contribution from an MSP signal is big enough to degrade the signal localization, where it can be seen that the PSF curve is skewed towards the nominal probing depth, indicating that the photons multiply scattered within the medium before this depth have more chances of surviving to reach the detector. Moreover, the photons backscattered from a very shallow depth at approximately 5 μm still survive the scattering to meet the criterion of Eq. 48.17 for depth localization at 50 μm. With an increase in probing depth to 150 μm, the PSF is overwhelmed by the MSP signal with only a few photons belonging to the LSP category. At this depth the signal localization is totally lost for OCT imaging. Furthermore, the axial resolution and imaging contrast are greatly reduced. The claim of high-resolution optical imaging of OCT is therefore questionable for highly scattering biological tissues. The axial resolution of OCT imaging is dependent on the optical properties of tissue and is a function of depth.
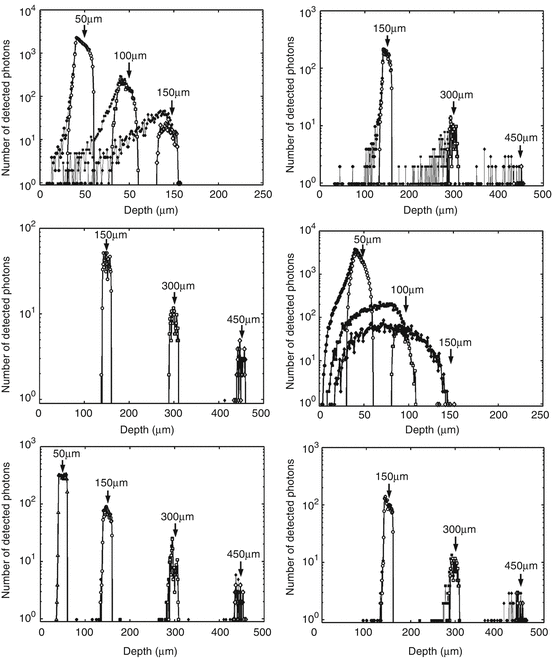

Fig. 48.5
Depth point spread functions (solid symbol curves) at different probing depths as indicated for the turbid media representing moderate scattering (μs = 10 mm−1) in the left column and high scattering (μs = 67 mm−1) in the right. From top to bottom, g = 0.7, 0.9, and 0.98, respectively. The LSP photons are plotted as the curves with hollow symbols [32]
Figure 48.6 illustrates the measured axial resolution from the simulation results as a function of depth for the cases of (μs, g) = (67 mm–1, 0.7), (67 mm–1, 0.9), and (10 mm–1, 0.9), respectively. The axial resolution of the OCT system is merely kept up to the depth of 50 μm for the case of (μs, g) = (67 mm–1, 0.7). After this depth, the actual axial resolution degrades exponentially with the increase of depth, where it becomes approximately 220 μm at the depth of 200 μm as opposed to the system resolution of 40 μm. With the increase of g to 0.9, this performance has been improved, with system resolution retained up to a depth of 100 μm. If in the meantime the scattering coefficient of the medium is reduced, for example, to μs = 10 mm–1 in this case, the probing depth at which imaging resolution is retained to the theoretical value would dramatically improve. This result is particularly welcome for the optical clearing of tissues with the purpose of enhancing the imaging depth of OCT which will be discussed in the next section.
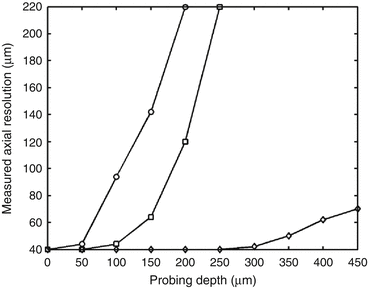

Fig. 48.6
The measured axial resolution from the simulation results plotted as a function of the probing depth for (μs, g) = (67 mm−1, 0.7) (circle), (67 mm−1, 0.9) (square), and (10 mm−1, 0.9) (diamond), respectively [32]
With the reduction of the scattering coefficient (compare the left and right columns in Fig. 48.5), signal localization improves with the lesser MSP signal contributing to the depth of PSFs. This indicates that the low-scattering medium offers the more localized signal at any probing depth, which alternatively implies that the light penetration depth, i.e., optical imaging depth, is enhanced with less deterioration of the imaging resolution as stated above. On the other hand, it can be clearly seen from Fig. 48.5 that with increasing g, the signal localization at any depth for the scattering medium improves dramatically, where the highly forward-scattering medium, i.e., g = 0.98, offers the best signal localization for all the cases investigated, see the bottom two figures for μ s = 10 mm–1and μ s = 67 mm–1, respectively. In these cases, only a few photons from the MSP category survive the scattering to contribute to the final PSF at a depth of up to 600 μm.
From these results, the advantage of reduction of scattering in the tissue in the enhanced OCT imaging performance is clearly seen. Here, we also see the importance of g factor in the OCT imaging for which the detailed investigation still remains to be explored.
48.4 Enhancement of Light Transmittance
Optical clearing effect on the reduction of multiple scattering through the use of biocompatible chemical agents has been experimentally investigated by a number of groups. The impregnation of the sclera, skin, human gastrointestinal tissues, cartilage, and tendon with x-ray contrast agents (Verografin, Trazograph, and Hypaque-60), glucose, propylene glycol, polypropylene glycol-based polymers (PPG), polyethylene glycol (PEG), PEG-based polymers, glycerol, etc. [27, 34–62], all shows the optical clearing effect in the visible and NIR wavelength ranges. A number of studies used near-infrared spectroscopic technique to quantitatively assess the light transmittance and scattering after the application of chemical agents [54–58]. With the use of Varian Cary 500 spectrophotometer with an internal integrating sphere, Fig. 48.7a, b gives an example of the measurement of the shift of transmittance and diffuse reflectance spectra, respectively, over the range of 800–2,200 nm as a function of time when the native porcine stomach pyloric mucosa specimen was applied with 80 % glycerol. The curves shown in the Figure were obtained at the time intervals of 0, 5, 10, 20, and 30 min, respectively, from bottom to top for transmittance (Fig. 48.7a) and from top to bottom for reflectance (Fig. 48.7b). It can be seen from Fig. 48.7 that, over the whole wavelength range investigated, the transmittance was increased with time. Diffuse reflectance was decreased over the range of 800–1,370 nm. The greatest increase in transmittance was at 1,278 nm, and the greatest decrease in reflectance was at 1,066 nm.




