(44.1)
where j is the pixel number index of the CCD camera in the spectrometer, t is the timing when an A-line is captured, E R is the light reflected from the reference mirror, S(k) is the spectral density of the light source used, n is the refractive index of the tissue, z is the depth coordinate within the sample, a(z, t) is the amplitude of the back scattered light, and v is the velocity of moving particles such as blood cells in a blood vessel, which is located at a depth z 1.
To extract the depth information from a Fourier-domain OCT system, a Fourier transform (FT) is used on the interference contributions of all the pathlength differences from each wavenumber, which is given by
![$$ I(z)=FT\left[I(k)\right]=M(z){e}^{i\varphi (z)} $$](/wp-content/uploads/2017/03/A76297_2_En_45_Chapter_Equ2.gif)
(44.2)
The result of the Fourier transformation is a complex valued signal that has a phase (φ(z)) and a magnitude (M(z)) terms.
The analysis of M(z) enables the reconstruction of the OCT structural image, which is commonly used on most OCT applications. Often, this refers to anatomical OCT, because it provides information about the microstructural features about the sample. For example, commercial OCT eye imaging systems analyze the thickness of the different retinal layers with micrometer resolution. The anatomical OCT is limited to providing morphological information; however, it does not provide functional information.
The value of φ(z) is a random phase caused by the microstructures located at the depth z. The analysis of the dynamic changes in the phase signal has been used for measuring tissue movement, which has allowed for the quantification of several tissue properties, such as the displacement of the trabecular meshwork in the anterior segment of the eye [14], the skin elastic properties [15], and the tissue photothermal responses [16]. The phase information has also been used to analyze the Doppler effect that is caused by the scattering of light from a moving object. This analysis enables the quantification of the axial velocity of moving particles such as red blood cells inside patent blood vessels. However, this technique is limited to fast flow velocities and is unable to quantify the blood flow velocities within capillary tissue beds.
By analyzing the dynamic changes in the magnitude, phase, or both, it is possible to extract the three-dimensional location of the patent blood vessels within the biological tissue, thus recreating the blood vessel microangiography. In the following sections we provide an overview of several techniques that have been previously used to extract the vessel microangiography.
44.2.1 Phase-Based Methods
Phase-based methods are established by analyzing the dynamic changes in the phase term (φ(z)) of the OCT signal. The axial displacement of a moving scatterer, such as a red blood cell, adds a Doppler shift to the carrier frequency, which can be measured by an OCT system through its phase. The disadvantage of these methods is that they are sensitive to the OCT system’s phase noise and the tissue’s bulk-motion artifacts.
44.2.1.1 Doppler Method
Doppler optical coherence tomography (DOCT) is an extension of OCT which combines the Doppler principles with OCT. The method was first used for analyzing the frequency shift due to the Doppler effect [17]. DOCT provides in vivo images of blood vessels, blood flow direction, and blood flow velocity, with good sensitivity [18]. This method is sensitive to the phase term; therefore, the phase stability of the OCT system is critical for obtaining high-quality images.
The phase difference is calculated between two A-lines captured at the same or at highly overlapping spatial locations [19]. The axial blood flow velocity (V z ) depends on the time interval (Δt) between the captured A-lines, which is given by
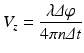
where λ is the wavelength of the light, Δφ is the phase difference between the time points, and n is the index of refraction of the sample. The maximum resolvable velocity is limited by the 2π ambiguity of the phase measurements; therefore, the phase changes are constrained by π and –π. The minimum velocity that can be resolved by this method is dictated by the system’s phase stability and the bulk tissue motions. As a result, this method has difficulty in determining the slow flow velocities from small blood vessels, such as capillaries.
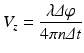
(44.3)
Measurement of the absolute blood flow velocity (V) is important in several studies, such as retinal imaging, since it allows for the evaluation of the blood flow dynamics within individual vessels. To obtain the absolute velocity, it is important to determine the angle (Φ) between the flow velocity vector and the vector of the incident OCT light, also known as the Doppler angle. The Doppler angle may be determined by using the three-dimensional OCT data set and the following equation [20]:
where dx, dy, and dz are the directional components of the blood vessel. The calculation of the total blood flow velocity can be obtained from
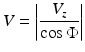
(44.4)
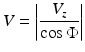
(44.5)
The total blood flow within a vessel is then calculated by multiplying the total velocity times the cross-sectional area of the vessel. Another method that has been proposed to calculate the total blood flow, which does not require the calculation of the Doppler angle, is to integrate the axial velocity in the xz plane (en face) [21], a method borrowed from Doppler ultrasound imaging. Given that the surface normal is parallel to the components of the velocity that is measured, the following expression can be used:
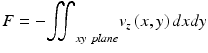
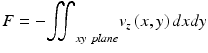
(44.6)
Averaging the phase differences between several A-lines causes a systematic error which is dependent on both the signal-to-noise ratio and the proximity of the measured velocity to the limits of the velocity range [22]. An improvement has been devised by using an extension of the Kasai autocorrelation algorithm [23], which can obtain the phase difference (Δφ) given by
![$$ \varDelta \varphi \left(z,t\right)=\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}\left[\frac{{\displaystyle {\sum}_{m=1}^N}Im\left[I\left(z,{t}_n\right)\times {I}^{*}\left(z,{t}_{n-1}\right)\right]}{{\displaystyle {\sum}_{m=0}^N}Re\left[I\left(z,{t}_n\right)\times {I}^{*}\left(z,{t}_{n-1}\right)\right]}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_45_Chapter_Equ7.gif)
where N is the number of phase differences that are going to be averaged together and * indicates the complex conjugate.
(44.7)
44.2.1.2 Phase-Resolved Doppler Variance
Phase-resolved Doppler variance [24–26] methods have been developed to detect small phase variations from microvascular flow and are based on using the bandwidth of the Doppler frequency spectrum. These methods have the advantages of being less sensitive to the pulsatile nature of the blood flow and the incident angle, as well as the capability of being able to monitor transverse flow velocities [27]. Several Doppler variance algorithms have previously been compared [28]; however, they are based on the autocorrelation principles:
![$$ {\sigma}^2=\frac{1}{\Delta {T}^2}\left[1-\frac{\left|{\displaystyle {\sum}_{j=1}^J}{\displaystyle {\sum}_{z=1}^N}\left({I}_{j,z}{I_{j+1,z}}^{*}\right)\right|}{{\displaystyle {\sum}_{j=1}^J}{\displaystyle {\sum}_{z=1}^N}\frac{1}{2}\left({I}_{j,z}{I_{j,z}}^{*}+{I}_{j,\mathrm{z}+1}{I_{j,z+1}}^{*}\right)}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_45_Chapter_Equ8.gif)
where J is the number of A-lines that are averaged and N is the number of depth points that are averaged. The averaging along the lateral and depth direction can reduce the background noise and improve the image quality although it may degrade the spatial resolution. The chosen values for J and N will depend on the specific biological tissue application. One drawback of the phase-resolved Doppler variance methods is their lost ability to provide the values of flow velocity.
(44.8)
44.2.2 Magnitude-Based Methods
In many applications, such as in imaging the retinal blood vessels, the direction of the vessels are nearly perpendicular to the OCT beam. As a result the axial velocity is small which yields a low-signal-to-noise ratio on the phase data. In other cases, there is low phase stability in the OCT system, such as in the application of several swept source OCT systems, where a source of phase noise is introduced from the cycle-to-cycle tuning and timing variability [29]. For these cases, the use of the phase information is highly susceptible to error. Therefore, methods have been developed that can obtain the angiography of the blood vessels based only on the temporal changes in the magnitude of the OCT signals. Such methods have less dependence on the beam incident angle, system phase stability, and small sample motion, thus are attractive in some of the applications in which only vascular morphology is of interests.
44.2.2.1 Autocorrelation Methods
Autocorrelation methods have been developed to quantitatively map the transverse particle-flow velocities. The method is based on analyzing the statistical nature of the intensity fluctuations of the backscattered light, which is modulated by flowing particles [30]. For example, Fig. 44.1 shows the magnitude of the detected OCT signal obtained from a flow phantom with different velocities, as well as the autocorrelation curves. The slope of the normalized autocorrelation function is proportional to the transverse velocities (Fig. 44.1d), as demonstrated in Fig. 44.2.
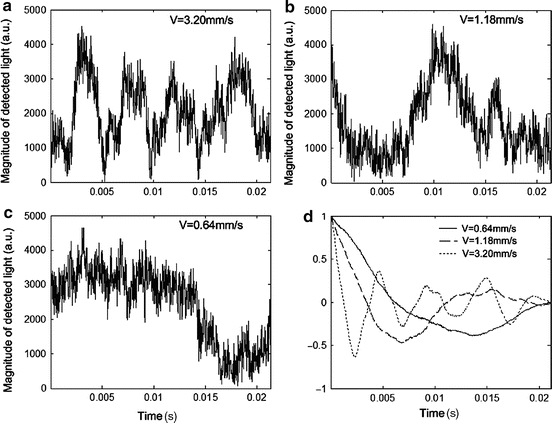
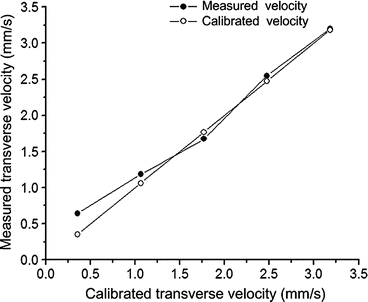
Fig. 44.1
Magnitude of the detected light which was modulated by intralipid flowing particles through a syringe pump phantom at the velocities of (a) 3.20 mm/s, (b) 1.18 mm/s, and (c) 0.64 mm/s. (d) Normalized autocorrelation function (Modified figure reprinted with permission from Ref. [30])
Fig. 44.2
Measured transverse velocities (line with solid circles) and calibrated velocities (line with open circles) (Modified figure reprinted with permission from Ref. [30])
44.2.2.2 Correlation Methods
Another method that has been widely used is analyzing the correlation among B scans. This method consists of determining the average correlation (D) value between several pairs of OCT frames at the same cross section. The average correlation can be expressed by
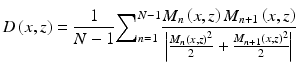
where N is the total number of frames at the same cross section and M n (x, z) and M n+1(x, z) are the amplitude signal from adjacent frames. Methods have been devised to minimize noise such as using a window of several pixels instead of a single pixel; however, this produces a reduction in its spatial resolution. The value of |D| varies between 0 and 1, where 0 indicates no correlation and 1 indicates high correlation. Therefore, static tissues have high absolute correlation values, while noise pixels and pixels that contain blood vessels have low absolute correlation values. For this reason, typically a structural mask is used over the cross-correlation map in order to eliminate the noise pixels, which adds an additional layer of complexity to this approach.
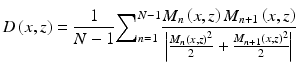
(44.9)
44.2.2.3 Speckle Variance
Speckle variance OCT (svOCT) is a functional extension of OCT, which can yield three-dimensional vascular images by analyzing the Fourier transform of the temporal variation of the speckle [35] or by calculating the interframe variance (SV ijk ) of N consecutive B-mode OCT structural intensity (M ijk ) images. By analyzing each individual pixel within the image and using N frames for the analysis, the variance is calculated with the following expression [36]:
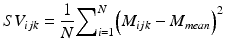
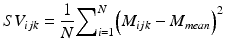
(44.10)
Given that the vascular regions decorrelate faster compared to their static counterparts, the speckle patterns produced yield an endogenous contrast that is used for extracting the blood microangiography.
44.2.3 Complex-Based Methods
Up to this point, we have determined ways of extracting the vessel microangiography using the magnitude or the phase information obtained from the OCT measurements. The phase-based methods are sensitive to the movements of the scatterers in the axial direction, while the magnitude-based methods are sensitive to the movements in both the lateral and the axial directions. Given that the OCT signal is a complex value, it is possible to take advantage of both the magnitude and phase information simultaneously to extract the vessel microangiography.
44.2.3.1 Optical Microangiography (OMAG)
Optical microangiography (OMAG) is a recently developed imaging technique that produces three-dimensional images of dynamic blood perfusion within microcirculatory tissue beds [37, 38]. OMAG was initially based on full range complex Fourier-domain OCT [39, 40], in which a high-pass filtering of the real valued signal is essentially employed to extract the blood flow signal from the static background signal. In OMAG, Wang et al. used a high-pass filter over the complex signal, to take advantage of both the magnitude and phase information. This process allows for the isolation of the positive and negative blood flow velocities [37].
OMAG analyzes the spatial frequency of the time-varying spectral interferograms. This analysis enables OMAG to separate the signal that is backscattered by static particles, such as bulk tissue, from moving particles, such as blood cells. There have been two generations of OMAG. The first generation consisted of introducing a carrier frequency by adding a phase delay to each A scan using a moving reference mirror or an off-pivot scanning beam. However, this technique is dependent on the precise synchronization of the reference arm modulation and the B-scan acquisition. As a result, it requires expensive modulators and is unable to detect bi-directional flow within a single B scan. The second generation overcame this limitation by using an algorithm which included a modified Hilbert transform that is used without the need of a spatial frequency modulation. This new algorithm is applicable for both the spectral domain and swept source OCT, provided that they both have comparable B-scan acquisition rates. The second generation OMAG requires only one B scan to obtain both the positive and negative flow.
The theory of OMAG is based on the depth-encoded spectral interferogram, which is captured by the linear detector as a real function B(z, t), and can be expressed as
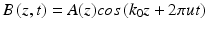
where A(z) is the reflective coefficient of the scatterer, k 0 is the wave vector of the detected light, and z relates to the detecting path. To simplify the expression we have ignored the random phase arising from the refractive index and assume that A(z) is constant along the B-direction, t is the B-scan time that corresponds to the different lateral positions, and u is the modulation frequency generated by the flow speed. The Fourier transform of the spectral signal B(z, t) is expressed by
![$$ H\left(z,u\right)=\frac{A(z)}{T_0}{\displaystyle \underset{t_0-\frac{\tau_0}{2}}{\overset{t_0+\frac{\tau_0}{2}}{\int }}} cos\left({k}_0z+2\pi ut\right){e}^{-i2\pi {u}_0t}dt=\frac{A(z){e}^{i{k}_0z} sin\left[\pi {\tau}_0\left(u-{u}_0\right)\right]}{2{T}_0\pi \left(u-{u}_0\right)}{e}^{-i2\pi \left(u-{u}_0\right){t}_0}+\frac{A(z){e}^{-i{k}_0z} sin\left[\pi {\tau}_0\left(u+{u}_0\right)\right]}{2{T}_0\pi \left(u+{u}_0\right)}{e}^{-i2\pi \left(u+{u}_0\right){t}_0} $$](/wp-content/uploads/2017/03/A76297_2_En_45_Chapter_Equ12.gif)
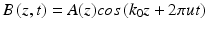
(44.11)
(44.12)
Based on the above equation, the nonmoving scatterers will be centered at the zeroth frequency (DC) region, and the moving scatterers will be shifted away from the zeroth frequency. Figure 44.3 presents examples of a frequency analysis using OMAG. If the tissue is completely homogeneous, which is an ideal case scenario, the frequency response would be a delta function centered at 0. However, a broadening of the spectra is observed when the tissue is inhomogeneous, which is a real case scenario. If there are moving particles within the inhomogeneous tissue, a higher frequency component will be observed. The shifting distance is directly related to the velocity u 0. The dynamic signal can be recreated by using a high-pass filter and then performing an inverse Fourier transform. The parameters that affect the flow signal detection include the flow velocity, the number and size of the moving scatterers, and the sampling line density.
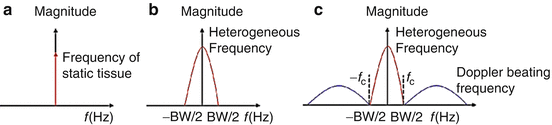
Fig. 44.3
Diagram of frequency components for different tissue sample: (a) an ideal tissue sample (optically homogeneous sample) with no moving particles, (b) a real tissue sample (optically heterogeneous sample) with no moving particles, and (c) a real tissue sample (optically heterogeneous sample) with moving particles (Modified figure reprinted with permission from Ref. [38])
By first using the OMAG method, it is possible to then apply the Doppler analysis method (Eq. 44.7), also known as Doppler OMAG (DOMAG). The key advantage of OMAG is that only the signals backscattered by the moving scatterers are obtained, and the static signal is filtered out. Therefore, the Doppler signal obtained in DOMAG is free of artifact induced noise. After the OMAG algorithm is applied, the correlation between adjacent A scans within the static tissue region is lost, which leads to a signal with high noise. However, this limitation is overcome by digitally reconstructing an ideal static background tissue which is optically homogeneous. This background tissue replaces the original heterogeneous tissue sample; therefore, creating correlated adjacent A-lines. Figure 44.4 presents a flowchart that highlights the algorithm used for the OMAG and DOMAG calculation.
Fig. 44.4
Flow chart showing the steps for DOMAG to evaluate the velocities of blood flow from a B-scan data set, I(k, t). The data coordinates are indicated in the lower right corner of each data block, where t is the time variable of probe beam scanning over a sample, k is the wavenumber, f is the spatial frequency, and z is the imaging depth. FT| t represents the Fourier transform (FT) against the time variable t in the B scan; FT −1 | f indicates the inverse FT against the spatial frequency, f; and FT|k is FT against the wavenumber k (Modified figure reprinted with permission from Ref. [38])
DOMAG has been demonstrated to be more sensitive to the phase velocities than simple Doppler analysis as in phase-resolved Doppler OCT [38]. Figure 44.5 presents a comparison of both methods.
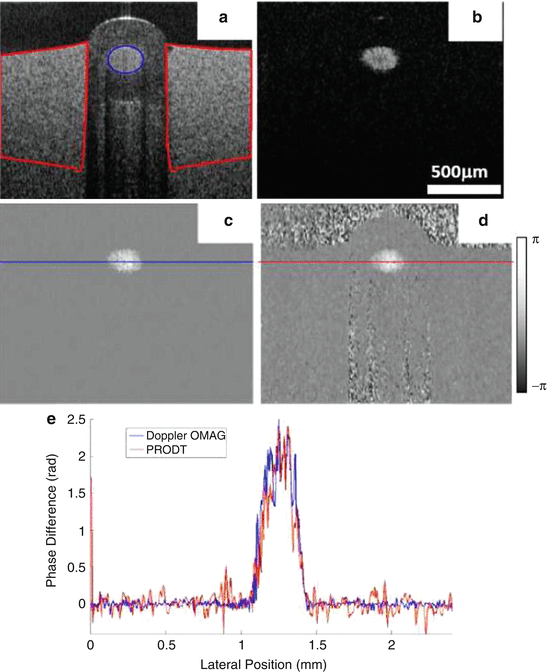
Fig 44.5
Flow phantom experiment results. (a) OMAG structural image, (b) OMAG flow image, (c) DOMAG velocity image, (d) PRDOCT velocity image, and (e) flow signal profiles extracted from the positions marked in (c) and (d) (Modified figure reprinted with permission from Ref. [38])
Figure 44.6 presents an example of a cross-sectional cut (B scan) obtained from a mouse brain with an intact skull. The location of the vessels and the Doppler signal can be observed.
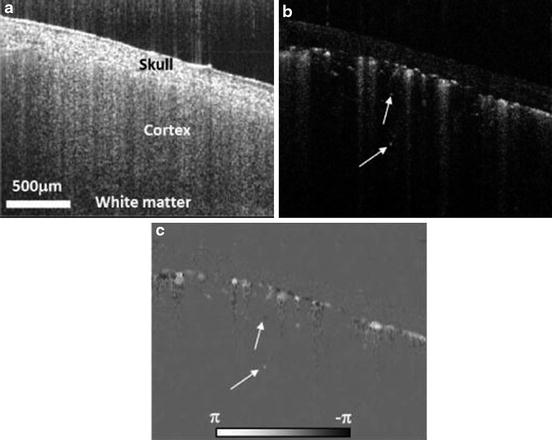
Fig. 44.6
In vivo OMAG image from a typical B scan of a mouse brain with the skull left intact. (a) OMAG image of the microstructures, identical to conventional spectral domain OCT image; (b) the corresponding OMAG image of blood flow; and (c) the corresponding DOMAG image of axial velocities of the blood flow (Modified figure reprinted with permission from Ref. [38])
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
