Fig. 11.1
Sketches of OCT configuration
11.1 Optical Design Considerations for OCT
11.1.1 Unique Optical Design Needs for OCT
OCT presents unique design needs different than, for example, microscopy or photography or laser scanning. Therefore, custom optical subsystems are typically designed especially for OCT and often for a specific application. For example, OCT sample scanning optics (II) are typically confocal systems that scan 0.05–0.1 NA beams over a range of several millimeters. Time-domain OCT (TD-OCT) systems typically use fast-scanning, reflective ODLs (III). In spectrometer-based frequency domain OCT (FD-OCT) (or spectral domain OCT, SDOCT) systems, the interfering spectra are collected by a linear array spectrometer (VI). The following six design considerations will be discussed:
1.
Clear sample spot profile
2.
Uniform chromatic coupling and high coupling efficiency
3.
Spectral response
4.
Depth of focus versus lateral resolution (numerical aperture)
5.
Frequency resolution
6.
Spectrometer spot size and falloff
Where items 1–3 are critical for the optical delay line design (III or IV), 1–4 are important for scanner optics (II), and 1–3 and 5–6 are key for the spectrometer designs (VI). The next three subsections b, c, and d will discuss these items in more detail. As a general principle, telecentric and achromatic optics will be used in the system designs to help achieve the design goals.
11.1.2 Sample Scanners
11.1.2.1 Clear Spot Profile
To achieve a high-resolution, high-contrast OCT image, a clean probe beam spot profile is necessary. Ideally, the clean spot profile will be maintained over the entire range of the scan, not merely on the optical axis. OCT makes two-dimensional or three-dimensional images by using spot scanning optics. The spot profile of the paraxial beam is usually closer to Gaussian than the skew beams or the beam significantly off the optical axis because of spherical and chromatic aberrations of the optical components. Sometimes, commercially available lenses with a small aperture are used to build scanners with a large lateral scanning range that degrades the spot profile toward the edge the lenses due to significant spherical and chromatic aberrations.
The use of certain lens types and design principles can be used to reduce design time, construction difficulties, and alignment issues. To minimize difficult design considerations, achromatic and aspheric lenses and a telecentric configuration are suggested in the sample arm scanner (II) design. Design software such as Zemax is usually a suitable tool for optimizing the spot profiles over the entire scanning range, while a beam analyzer is useful for measuring the real spot profile to optimize the assembled design [1]. The use of these tools will help to ensure a minimum amount of work and maximum results when designing OCT optical systems.
11.1.2.2 Uniform and High Coupling Efficiency
Coupling efficiency refers to any point where the light enters and or exits the OCT system. The efficiency refers to both the amount of power lost during transitions from, for example, air to fiber or fiber to air and the chromatic efficiency of the transitions. Proper consideration of these parameters will ensure that optimal use of the light source occurs, and maximum axial resolution is maintained throughout the length of the scan.
The sample scanner of an OCT system typically delivers the light to the sample and collects the scattered light back from the sample through the same optics, as shown in Fig. 11.1. The higher the coupling efficiency, the lower the source power that is needed to achieve the same image quality. Besides the neutral attenuation due to optical surfaces, both the spherical and the chromatic aberrations of the lenses affect the coupling efficiency. In most scanner designs, the light is delivered by an optical fiber to the scanner (II). The wavefront of the back-reflected (scattered) beam is changed because of spherical and chromatic aberrations. These changes result in both misalignment and mode mismatch between the fiber and the back-reflected beam, which lead to some loss of the coupling efficiency. Coupling efficiency may also vary as a function of the lateral scan position.
A telecentric optical configuration can minimize misalignment, while achromatic and aspheric lenses can minimize spherical and chromatic aberrations. Optical design software can help the designer create an optimum arrangement of the components to build a scanner with a uniform and high coupling efficiency.
11.1.2.3 Spectral Response
The spectral response of an OCT subsystem affects the axial resolution of the images, the system’s sensitivity to dispersion, and the degree to which optical corrections have to be made. Appropriate design, taking into account the spectral response, can ensure that image quality remains high even in conditions such as imaging through large volumes of water. Designing for an appropriate spectral response profile will result in optimal use of the bandwidth of the light source and the highest quality images.
The variation of the coupling efficiency as a function of wavelengths filters the spectrum of the light. The center wavelength, bandwidth, and amplitude are all altered by the optics and the sample between the light source and the detector. These variations may not be identical in the sample arm scanner (II) and the optical delay line (III or IV). In general, this filter function generated by the nonconstant spectral response of the optics affects the signal amplitude and the axial resolution of the OCT image [2]. Since the coupling efficiency may be different at different transversal positions, the spectral response will be different as well.
11.1.2.4 Depth of Focus Versus Resolution
To obtain high lateral resolution and large depth of focus are always the goals in an OCT scanner design. Unfortunately, the depth of focus and the lateral resolution vary inversely so that increasing the depth of focus typically worsens the lateral resolution. An optical designer must consider the tradeoff between the two parameters. The intended application must be carefully considered when designing these parameters.
Assuming the OCT beam is Gaussian, the depth of focus is defined as twice the Rayleigh range [3]:
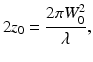
where W 0 and λ are the radius of the beam waist at focus and the wavelength, respectively. The Rayleigh range z 0 is measured from the waist to the spot size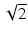 
times of the waist. For instance, if the wavelength is λ = 1.3 μm and the radius of waist is W0 = 5 μm, the depth of focus will be 121 μm. The dependence of the beam radius on z is expressed as
![$$ \begin{array}{l}W(z)={\left[{W}_0^2+{\left(\frac{\lambda }{\pi {W}_0}z\right)}^2\right]}^{1/2}\\ {}\kern2em ={\left[{\left(\frac{\lambda }{\pi {\theta}_0}\right)}^2+{\left(z{\theta}_0\right)}^2\right]}^{1/2},\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_12_Chapter_Equ2.gif)
where the beam divergence θ 0 = W 0/z 0 and the distance variable z is measured from the point of the waist. The value of sin(θ 0) is defined as the numerical aperture (NA). Equation 11.2 indicates that the spot size is smaller for a higher numerical aperture and that the higher the lateral resolution, the shorter the depth of focus.
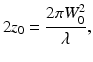
(11.1)
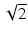times of the waist. For instance, if the wavelength is λ = 1.3 μm and the radius of waist is W0 = 5 μm, the depth of focus will be 121 μm. The dependence of the beam radius on z is expressed as(11.2)
11.1.3 Scanning Optical Delay Lines
11.1.3.1 Uniform Coupling Efficiency
In OCT, the function of the optical delay line (ODL) (III or IV) is to produce the optical path or the phase match with the sample arm (II). Numerous scanning ODL designs have been demonstrated [4]. Although only a small amount of reference light is needed, the coupling efficiency can affect system sensitivity. More importantly, the reference ODL should have a uniform coupling efficiency. The coupling pattern of the rapid scanning optical delay line (RSOD) is described in Sect. 11.3.
11.1.3.2 Spectral Response
The spectral response requirement in the reference arm or the optical delay line is of the same importance as discussed previously for the sample arm scanner design. Although the optics of the optical delay line are usually simpler than that of the sample scanner, they still normally create a nonuniform coupling efficiency over the spectrum. This creates a curved spectral response filter that operates on the spectrum of the light source. This spectral response is normally different from the spectral filter of the scanner, which results in a degradation of the amplitude and the axial resolution of OCT signal [2].
11.1.4 Spectrometers
11.1.4.1 Resolution
In spectrometer-based frequency domain OCT, three parameters primarily influence the quality of the spectrometer and hence the OCT image quality: the frequency resolution, spectral response, and spot size of the beam. These determine the falloff characteristic and the axial resolution of the image.
A spectrometer based on a linear detector array samples the spectrum illuminating the array, resulting in a discrete signal. The frequency interval of the pixels in the dispersive direction of the spectrum (i.e., the distance between each pixel) determines the un-aliased imaging range of FD-OCT according to the sampling theorem. The higher the frequency resolution, the longer the image range of the FD-OCT. Because the pixel number of the detector array is finite, the tradeoff between the imaging range and the axial resolution (spectrum bandwidth) should be considered in the spectrometer design.
11.1.4.2 Spectral Response
The spectral response of the spectrometer is important in the same way as discussed previously for both scanner and delay line designs. Besides going through the reference and sample arms, the light travels through the optics of the spectrometer before it is collected by the detector array. A nonuniform spectral response filters the interfering spectra, which changes the axial resolution and the contrast of the OCT image.
One of the design goals is to minimize the difference between the coherence spectra and the spectrum of the light source in order to achieve an optimum image quality. The design example of a spectrometer in Sect. 11.5.1 presents an example of a case where there is a trade-off between the flatness of the spectral response and the throughput of the spectrometer.
11.1.4.3 Spot Size and Falloff
The penetration depth of spectrometer-based FD-OCT is also limited by the signal falloff due to the interference fringe washout due to the window in frequency space. In other words, the falloff is mostly determined by the spot size of a single wavelength component of the beam illuminating the array and the pixel width of the detector in the spectral dispersion direction [5] such that the smaller the spot size or the pixel size, the better the falloff.
11.2 Some Key Optical Design Principles for OCT
11.2.1 Telecentric Optics
Telecentric optical systems are characterized by a flat imaging plane and are important to the design of OCT systems because they increase coupling efficiency. The flat imaging plane decreases the amount of post-image processing needed to display geometrically correct images and increases the coupling efficiency because the back-reflected light returns close to the same incident path.
The definition of a telecentric optical system is a system in which all of the chief rays on the image side are parallel to the local optical axis and perpendicular to the planar image plane. Telecentric optics generally reduce image artifacts caused by off-axis optical aberrations. This leads to several advantages for an OCT scanner, including constant magnification, constant spot size both on- and off-axis, and a flat imaging plane. Figure 11.2 shows the ray trace of three examples of approximately telecentric lens systems (modeled by Zemax) in which the stop is located at the front focus. Three collimated incident beams at different angles pass through the optical system and are focused on the almost-flat image plane at the back focus. All of the chief rays on the image side are parallel to the optical axis. This feature results in a maximum reflection or scattering from the sample at and around the focus and back through the same optics.
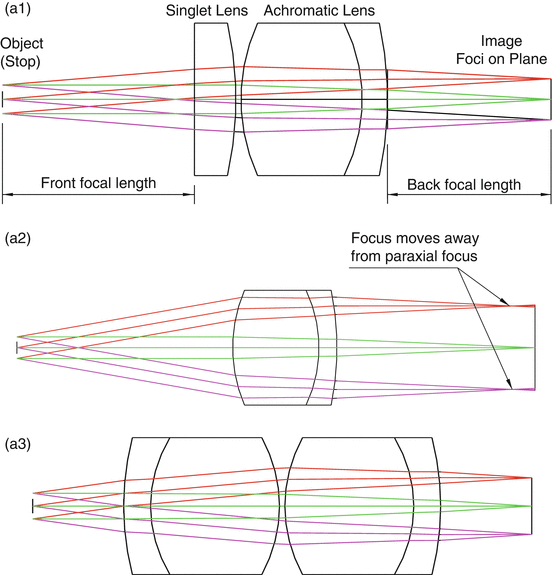
Fig. 11.2
Telecentric setup by Zemax
In Fig. 11.2(a1–a3), the foci of off-axis beams were closer to the lens than the paraxial focus by 0.36 mm, 3.15 mm, and 0.012 mm, respectively, for the three simulated configurations. Figure 11.2(a1) is sometimes the most economical configuration since a singlet is much cheaper than a second achromatic doublet (a3), yet the performance is much superior to a doublet alone (a2). For a telecentric design, the scanning mirrors of an OCT scanner (or their image) should be placed at the front focus of the optics, which results in a more consistent image quality over a wide lateral scanning range. It should be noted that telecentric optics do not necessarily require an achromatic doublet, but the achromatic doublet generally provides good performance.
11.2.2 Aspheric Optics
The use of aspheric optics in an OCT system provides several distinct advantages. First, it reduces the effects of spherical aberrations in the system. Second, because of this reduction, imaging spot profiles are more clean. Third, a clean spot profile results in an increased coupling efficiency.
The curvature of an aspheric surface varies with the height of the incident ray [6]. Aspheric surfaces are usually used to collimate a beam with a large numerical aperture. Spherical aberration is defined as the variation of the focus with the aperture, which is because a spherical surface is only an approximation of an ideal focusing surface. Figure 11.3(b1) is a somewhat exaggerated sketch of a simple lens forming an “image” of an axial object point a great distance away. The ray close to the optical axis comes to a focus (intersects the axis) very near the paraxial focus position. The higher the ray height at the lens, the farther the position of the ray intersection with the optical axis moves from the paraxial focus. The distance between the paraxial focus and the axial intersection of the ray is also called the longitudinal spherical aberration.
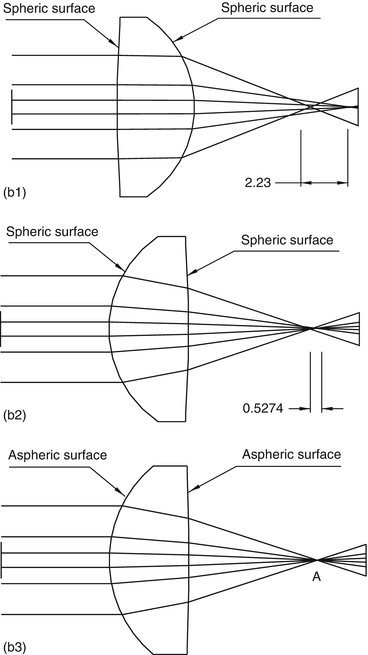
Fig. 11.3
A simple converging lens with under-corrected spherical aberration. (b1) The rays farther from the axis are brought to a focus nearer the lens; (b2) a correctly oriented spherical lens; (b3) an aspheric collimator
The spherical aberration can be improved by correctly orienting the lens. For instance, the aberration of the optics in Fig. 11.3(b1) was improved by just flipping this lens to Fig. 11.3(b2). It is always a preferred setup that the more curved surface faces the collimated beam and the less curved surface faces the focused beam. In order to achieve high-order removal of the spherical aberration, an aspheric lens should be used as shown in Fig. 11.3(b3).
11.2.3 Achromatic Optics
The use of achromatic optics in an OCT system has several advantages. They preserve axial resolution, reduce the dispersion effects of the optical system, improve coupling efficiency, and produce a clean spot profile. For these reasons, it is advantageous to use achromatic optics when designing an OCT system. Again, achromatic optics are more expensive, but the result is typically worthwhile.
Chromatic aberration is the longitudinal variation of focus (or image position) with wavelength. The refractive index of the glass varies as a function of the wavelength of light, which results in the focal length of the lens varying as a function of the wavelength. For most optical materials, the longer the wavelength, the lower the refractive index. This index feature of the material causes the short wavelengths to be more strongly refracted than the long wavelengths at the surface. For example, the blue light rays (shorter wavelengths) going through a simple positive lens are brought to a focus closer to the lens than the red rays (longer wavelengths) as shown in Fig. 11.4(c1) (detailed later). The distance along the axis between the two focus points is the longitudinal axial chromatic aberration [7].
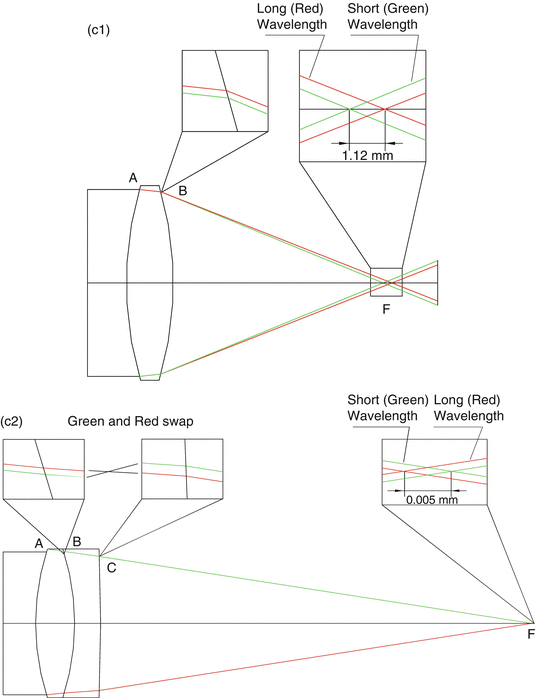
Fig. 11.4
Schematic diagram of chromatic aberration and correction by use of an achromatic doublet. The lens is simulated by Zemax. (c1) is a simple double convex positive lens and part of the doublet of (c2). (c2) is the achromatic doublet lens. Green and red represent the short and long wavelengths, respectively
To clearly demonstrate chromatic aberration, we virtually “dissected” an achromatic doublet lens (Edmund Optics 45805), shown in Fig. 11.4. The lens materials are, respectively, LAKN22 (index: 1.6536@550 nm; 1.6333@1,350 nm) for the AB layer and SFL6 (index: 1.8118@550 nm; 1.7665@1,350 nm) for the BC layer. The radii of curvature of surfaces A, B, and C are, respectively, 43.96 mm, −43.96 mm, and −321.46 mm. The center thicknesses are 6 mm for AB and 4 mm for BC. After the removal of the BC layer, Fig. 11.2c1 shows the significant chromatic aberration of a simple positive element. In Fig. 11.4(c1), the short (550 nm) and long (1,350 nm) wavelength rays incident at point A on the first surface of the lens were separated by the dispersion of the glass shown in the zoom-in window at point B of the second surface. The zoom-in window at focus F indicates an aberration of 1.12 mm for a beam with height of 12 mm and that the focal length of the long wavelength is longer than that of the short wavelength.
Compared to the first piece AB, the second piece BC is made of a glass with different dispersion and polished to lower power (curvature). Figure 11.4(c2) shows that an achromatic doublet lens is made by bonding pieces AB and BC together using an index matching epoxy. Observe that the positions of long and short wavelengths are swapped during propagation from surface B to C, and the longitudinal aberration at the focus is reduced to 0.005 mm from 1.12 mm for the wavelengths of 550 nm and 1,350 nm.
OCT optics must support broad optical bandwidths in order to achieve high-quality, high-resolution imaging.
11.3 Scanning ODL Design Example
All OCT systems require an optical delay line (ODL) to provide a reference field to interfere with the sample field. A FD-OCT system uses a fixed-path ODL, but a TD-OCT system requires a high-speed scanning ODL for real-time imaging. The most commonly used ODL for real-time TD-OCT in the Fourier-domain rapid-scanning ODL (RSOD) [8–11].
In this section, we will review the optical design and the performance analysis of the RSOD and demonstrate how to address the design requirements 2–3 in Sect. 11.1.1 and the use of telecentric and achromatic optics in Sects. 11.2.1 and 11.2.3. The coupling efficiency and the spectral response will be addressed by simulations using a Zemax model of a previously reported RSOD design [11]. Figure 11.5b1 shows a schematic drawing of the RSOD [11], while the Figs. 11.5b2, b3 are the Zemax models at two different scanning angles showing the ray propagation step by step on which we will discuss the design procedure.
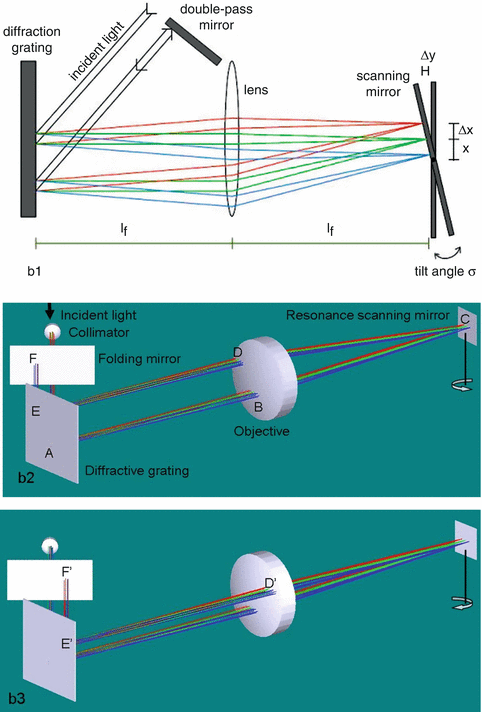
Fig. 11.5
Schematic of the Fourier domain optical delay line. (b1) The top view from ref. [11]. (b2, b3) Zemax modeling at two different scanning angles. Round trip by going through the fiber – collimator – A – B – C – D (D′) – E (E′) – F (F′) – E (E′) – D (D′) – C – B – A – collimator – fiber. The incident and output rays at the lower parts of the grating and the objective in b2 and b3. The folded part of the travel are scanning in horizontal lines from D to D′, E to E′, and F to F′ on the upper part of the objective, grating, and folding mirror, respectively
Figures 11.5b2 and b3 show that the collimated broadband light is dispersed by a diffraction grating at point A. The dispersed beam passes through the lower part of the objective at point B before it is focused onto a resonant scanning mirror at point C (an alternative design is a galvanometric scanning mirror). The objective collimates the spectrum and images or focuses every wavelength onto the scanning mirror. The resonant scanning mirror vibrates on a vertical axis reflecting the dispersed beam back to the upper part of the objective from D to D′. Then, the objective collimates each single wavelength and reconverges the spectrum to point E (through E′ when the resonant mirror scans) on the diffraction grating which recombines the dispersed spectrum into a single collimated beam and directs the collimated beam toward the folding mirror at point F (through F′ when the resonant mirror scans). To the folding mirror, one-half of the round trip is completed. The next propagation is identical to the first series but opposite in order. In summary, the ray finishes a round trip by going through the following steps: the fiber – collimator – A – B – C – D (D′) – E (E′) – F (F′) – E (E′) – D (D′) – C – B – A – collimator – fiber.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
