Fig. 15.1
OCT scanning and scanner coordinate system schematic. Left: 1D acquisition (A-Scan). A single depth profile is acquired which measures backscattered intensity vs. axial dimension (depth). Middle: 2D imaging (B-Scan). The OCT beam is scanned in a transverse direction while A-Scans (red arrows) are acquired. Right: 3D acquisition. Multiple B-Scans are acquired such that A-scans are sampled on a 2D grid in the transverse plane
The direction that is rapidly scanned in each B-Scan is called transverse direction or the fast direction. In contrast, the orthogonal direction on the grid is scanned much slower, hence its name slow direction. The effect of the priority scanning in one direction is that neighboring A-Scan samples on the grid along the slow scan direction are acquired much more apart from each other in time, compared to the fast scan direction.
OCT scanning takes place in a scan coordinate system that consists of x and y galvanometer mirror positions and axial depth along the light beam z. Given a static object that does not move relative to the OCT system, every set of galvanometer mirror positions maps to a certain beam path through the object. In combination with the axial coordinate z, a fixed relationship between scan coordinate system coordinates and positions on the object exists. However, especially in in vivo imaging, the relative position between the OCT system and the object can change over time. We can think of this as having another coordinate system called the object coordinate system that has a time-dependent relation to the scan coordinate system. Any relative motion between OCT system and imaged object changes this relationship.
OCT acquisition times in in vivo imaging can take as much as several seconds, due in part to the way spatial dimensions are encoded in time, the scan pattern used, and the speed of typical OCT systems. Object motion during this time leads to a deviation of the beam paths of individual A-Scans relative to the case of there being no motion. The deviation leads to the object being sampled at locations inconsistent with the time/space encoding and results in spatially distorted data. Motion can cause parts of the object to be imaged multiple times, while other parts might not be sampled at all. These effects cause errors in quantitative measurements on the OCT data that rely on the accurate measurement of spatial features of the object. If multiple spatial dimensions are encoded, we can expect that the potential distortion that is caused by motion is much larger in the direction that has the larger acquisition time difference between samples, i.e., the slow scan direction in a 3D raster scan pattern. Conversely, if the encoding is done very fast relative to the speed of the relative motion, the motion is effectively frozen out and the image shows no noticeable spatial distortion. This is, for example, the case for a 2D B-Scan image on a commercial Fourier domain OCT system of the current generation.
Motion correction approaches in OCT try to enforce that the individual A-Scans of a corrected acquisition show the expected locations, regardless of motion during the acquisition. In the following sections, we restrict ourselves to the motion problem and possible solutions in the context of OCT imaging of the retina. This is because retinal imaging is the most important in vivo application of OCT and the focus of most efforts in the area of motion correction.
15.3 Retinal Imaging
OCT is a standard of care for ophthalmologic examinations of the retina due to its high resolution and noninvasiveness. It has key applications in early detection and monitoring of common eye diseases such as glaucoma and age-related macular degeneration (AMD). As such, it is important for quantitative measurements that are extracted from retinal OCT data to be reliable and reproducible. However, when imaging the eye in vivo, several sources of motion are not avoidable and motion artifacts occur that limit the reliability of quantitative measurements. In the following sections, we consider aspects of ophthalmologic imaging that are relevant to the motion correction problem.
15.3.1 Eye Optics/OCT Scanning
One peculiarity of retinal imaging is that the eye itself becomes part of the optics of the system, i.e., the combination of cornea and lens of the eye focuses the OCT beam onto the retina. This is different from an OCT microscope, for example, where all the optical elements such as lenses are fixed relative to the system. In retinal imaging, ideally the eye is aligned to the OCT system such that the scanning OCT beam is pivoted in a fixed point P pivot in the center of the pupil of the eye. This minimizes vignetting of the beam by the pupil of the eye and enables imaging the largest possible area on the retina. Figure 15.2 shows a schematic view of the optics involved for imaging the retina. The OCT beam is collimated incident on the cornea which in combination with the lens focuses the beam onto the retina. Scanning of the retina is performed by changing the incident angles of the OCT beam relative to the optical axis using galvanometer mirrors. The eye optics maps the two incoming angles in x and y direction onto corresponding angles on the retina. Since the OCT beam is pivoted during scanning, the beam paths for each A-Scan during a linear scan create a fanlike pattern on the retina. This means that the beam paths of neighboring A-Scans are not actually parallel. When the OCT data is displayed though, the individual A-Scans are seen as parallel lines that form 2D and 3D images. Therefore, the OCT data is displayed as a 2D or 3D function of one or two galvanometer mirror positions and an axial depth. This representation maps approximately to Euclidian coordinates on the retina. However, for considering the possible effects of motion, it is important to consider the actual scan geometry.


Fig. 15.2
Baseline situation of imaging an eye using OCT. A collimated beam originating from the OCT system passes through cornea and lens and is focused onto the retina. By changing the angle of incidence of the beam on the eye, the beam is scanned over the retina. During scanning, A-Scans are acquired (red lines). Because of the optics of the eye, the A-Scans are in a fanlike geometry. An OCT image is created by showing these A-Scans as parallel lines (right image)
15.3.2 Motion Types/Effects
In eye motion, we can distinguish between transverse eye motion and axial eye motion. These names relate to the direction of displacement they cause within the scan coordinate system. Transverse eye motion is equivalent to a change in fixation of the subject. Here, muscles rotate the eyeball in the left/right and up/down directions. Transverse motion can further be subdivided into slow drifts of fixation and fast saccadic motion. Saccadic motion typically occurs up to two times a second and can lead to a change in fixation angle of up to 4° [2, 3]. The duration of saccadic motion itself can range from 20 ms to 100 ms and can be very fast with angular velocities of up to 300° per second [4]. The second fundamental type of eye motion is motion in the axial direction. This is equivalent to the eyeball and/or retina moving toward or away from the OCT system. Axial eye motion can be caused by changes in blood pressure caused by the heartbeat and by respiration. Compared to saccadic transverse motion, axial motion is slow and has low frequency. Figure 15.3 shows an example of the effect of different types of motion on a 3D-OCT data set.
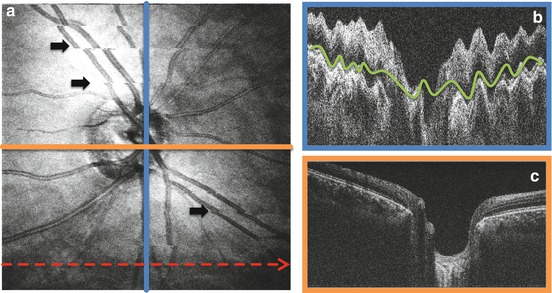

Fig. 15.3
Example of motion artifacts in a raster-scanned 3D OCT volume. The volume consists of 400 by 400 A-Scans sampled over 6 by 6 mm centered on the optic nerve head. The system was running at 90 kHz A-Scan rate, leading to a total acquisition time of approximately 2.5 s including flyback. (a) En face fundus projection of the volume. The dotted red line marks the fast scan direction of the volume. The black arrows indicate motion artifacts caused by transverse eye motion that create discontinuities in the vessel pattern. (b) Excerpt of the central slice of the volume along the slow scan direction (blue line in a). Axial motion leads to a wavy deformation of the retina in axial direction (green curve). (c): Excerpt of the central slice of the volume along the fast scan direction (orange line in a). The spatial structure of the retina remains intact along the fast scan direction
Motion of the eye relative to the system causes two primary effects: For one, the angle of incidence of the OCT on the pivot point can change. The second effect is that the actual pivot point of the combined system can deviate significantly from the ideal pivot point p pivot . Assuming that only the incident angles change about δx and δy and that the pivot point stays the same, this change in incident angle gets transformed to a change in angle within the coordinate system of the retina. The incident angle can also be changed using the galvanometer mirrors, though. Given the right correction on the mirror angles, the beam path can be the same as if there was no eye rotation. Therefore, if the beam always pivots a single point, transverse motion of the eye causes a transverse displacement of the beam on the retina that could also be reached by applying an offset to the incident galvanometer mirror positions.
If due to motion the actual pivot point is different from the reference pivot point p pivot , the light focuses at the same lateral position on the retina; however the optical path length changes. The dominant effect is a translation of the A-Scan content in the axial direction. This is usually seen as an axial tilt of the retina within the B-Scan. A secondary effect is that the incident angle of the A-Scan on a specific position on the retina changes with beam translation in the pupil plane. This means that the actual beam path through a certain point on the retina deviates from the beam path of a normally pivoted point. Both beams intersect in the same point on the retina, but due to the different angle of incidence, the beams do not sample the same transverse positions closer and farther down the axial dimension. If this effect were significant, it would mean that the effect of a change in pivot point could not be compensated by applying an offset on the galvanometer positions.
As an example for the size of this effect in a typical eye, a simulation using ZEMAX and an eye model was performed. A 2 mm translation of the beam in the pupil plane results in a change in the angle of incidence of the OCT beam on the retina of about 5°. Over the thickness of the retina of about 300 μm, the maximum deviation in the beam path which is caused by the change in pivot point is 13 μm. This is less than a typical spot size diameter of 20 μm. Also, this deviation is two orders of magnitude smaller than the effects of eye rotation. Assuming a typical pupil size of the eye of 4 mm and an OCT beam diameter of 2 mm incident on the pupil, any greater shift in beam position would already cause vignetting of the beam by the pupil, causing visible signal loss in the OCT data set. Furthermore, according to [2], the angular rotation induced by involuntary eye motion such as drifts and saccades does usually not exceed 4°. Using the simplifying assumption that the eye is spherical with a radius of about 11 mm and rotates around the center of the sphere, a 4° rotation corresponds to a lateral translation of the pupil with respect to the OCT beam of about 0.8 mm (displacement = sin(α)radius). This is well below the 2 mm shift for which the minimal change of the beam path was calculated and therefore leads to an even smaller effect.
In practice, both the incident angle and the pivot point position change because of motion. However, from these simplified sample calculations, we can conclude that in ophthalmologic imaging, the effects of eye motion in transverse and axial direction move the content of the A-Scan in a way that is consistent with applying a corresponding offset to the galvanometer positions and moving the content of the A-Scan in axial direction. Higher-order effects such as those resulting from a change in pivot position can be considered negligible for explaining the effects of normal eye motion. This is consistent with the effects that are due to motion and are observed in practice.
Figure 15.4 shows a schematic view of the relation between the scanner and object coordinates under the effects of motion. Due to saccadic motion of the eye, the relation in the transverse coordinates between the scan and object coordinate system changes rapidly. This leads to discontinuities in the acquired en face fundus projection. In addition, certain areas are missed during scanning, while others are imaged repeatedly. For a certain A-Scan, the difference in position between the two coordinate systems corresponds to the deviation in galvanometer mirror positions that was caused by motion at the time the A-Scan was acquired.


Fig. 15.4
Schematic showing relation between object and scanner coordinate system when affected by motion. Left: En face view in the scanner coordinate system. Dotted colored arrows indicate B-scans; dots indicate individual A-scans. The background shows an en face fundus projection as it would be acquired given motion. The two red arrows indicate discontinuities from motion. Right: En face view in the object coordinate system. Corresponding color arrows indicate where B-scans from the scanner coordinate system are located in the object coordinate system. The background shows an en face view of the object in the object coordinate system
15.4 Motion Correction Approaches
Since motion artifacts constitute a serious issue, especially for retinal OCT imaging, considerable work has been performed by different groups to help solve the problem. In the following sections, we give an overview of the state of the art in OCT motion correction techniques.
One basic feature of a particular motion correction technique is whether it needs additional hardware support, i.e., the OCT system needs to be built with the motion correction technique in mind or additional imaging modalities need to be available. There are two basic ways to address the problem. Hardware-based methods try to avoid motion artifacts during the acquisition itself though a specific system design:
Freeze out motion by improving the encoding of spatial dimensions in time, i.e., acquire the data set in a shorter time.
Measure the deviations that originate from changes in relative position, and actively apply corrections to the galvanometer mirror positions during acquisition: tracking OCT.
Software-based methods on the other hand try to correct motion artifacts retrospectively using image processing:
Use images from another modality that does not suffer from motion artifacts as OCT does as a reference to correct the OCT data.
Correlate consecutively acquired data to filter out the effects of motion.
Correct motion artifacts using additional OCT data with orthogonal fast scan axis.
In the following sections, we review selected state-of-the-art methods for each approach.
15.4.1 Hardware-Based Methods
15.4.1.1 High-Speed OCT
One fundamental way to alleviate the motion artifact problem in OCT is to increase the imaging speed of the OCT system, which continues to be important. Higher speed means that a higher number of A-Scans can be sampled per unit of time and that therefore a certain scan pattern can be sampled in less time. Since motion requires time to pass, short enough acquisition times can effectively be used to “freeze out” motion in parts or even in the whole OCT acquisition and minimize motion-induced spatial distortion.
Historically, the move from time domain to Fourier domain OCT [5] enabled an order of magnitude increase in acquisition speeds. This was mainly due to the inherent advantage of sensitivity of Fourier domain OCT [6]. In addition, the reference arm did not need to be scanned anymore during the acquisition of a single A-Scan. It is a reasonable assumption in time domain OCT that there is effectively no motion within an A-Scan. The higher speed of Fourier domain OCT systems allows current commercial systems to effectively disregard motion within a single 2D B-Scan, simply because the acquisition time is short enough compared to the speed and frequency of eye motion.
Within the realm of existing Fourier domain OCT technology, it has been shown that system speed can be improved tremendously with respect to standard commercial systems which operate at around 25 kHz A-Scan rate. Using Fourier domain mode locked (FDML) swept source lasers, retinal OCT operating at up to 6.7 MHz has been shown [7–9], albeit with reduced sensitivity and resolution compared to commercially available systems.
There is an inherent sensitivity loss associated with running faster than the maximally allowed light exposure on the eye, which is limited by safety standards. This puts an upper bound to the number of photons that can be collected per unit of time. Now, if one runs twice as fast, there are only half as many photons available to be collected per A-Scan. All other things being equal, this means that one pays an increase in speed with a loss in sensitivity. Especially for clinical applications, where subjects might have bad eye optics, opacities, and floaters, system with sufficient sensitivity headroom is necessary for imaging.
Another issue is that one might want to use the high speed of a system not just to lower the overall acquisition time and motion artifacts. Instead one might choose to acquire more A-Scans in total, e.g., to sample more densely and/or to sample a larger area. This trade-off depends on the concrete data that one wants to collect.
Pending significant improvements in sensitivity, speed alone is unlikely to be the only solution to motion artifacts in OCT, at least as long as dense sampling of a clinically relevant area with good sensitivity and resolution is required. Such improvements might come from entirely alternative forms of OCT such as full-field OCT which has already been demonstrated for retinal imaging [10]. This technique illuminates the full field at once and does not require the scanning of the OCT beam. This helps in achieving high speeds and allows for a higher light exposure. However, as of now, low sensitivity and axial resolution as well as issues with cross talk and uniform image quality limit the practicality of the technique.
15.4.1.2 Tracking OCT
The approach of tracking OCT is to continuously measure the motion-induced deviation from a reference position and to apply a corresponding offset to the galvanometer mirrors and/or the reference arm mirror to cancel this deviation, effectively compensating for the deviation in scan position that is caused by object motion and therefore removing motion artifacts. Key factors in tracking OCT are the accuracy of measurement of the deviation and its correction and the update rate of the system, i.e., how fast the system can react to a motion-induced change in relative position.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


