Fig. 66.1
Calculation of CBF from Doppler OCT measurement of the flow velocity. (a) Blood vessels can be oriented at any angle φ relative to the incident light. (b) The area of the vessel in the en face (xy) plane is inversely proportional to cos(φ). (c) En face cut at a depth of 50 μm through a 3-D map of the axial velocity (averaged over ten volumes). (d) Zoom of a venule showing the axial component of flow velocity over the vessel cross section (upsampled to reduce pixellation). While the area of the vessel in the xy plane is inversely proportional to cos(φ), the axial component of the velocity is proportional to cos(φ). Therefore, the flow F can be obtained from the en face map of the axial velocity, v z (x,y) (Reprinted from [12] with permission)
Doppler OCT imaging of CBF displays features characteristic of general blood flow, including conservation along non-branching vascular segments and at branch points [13]. For example, Fig. 66.2 shows how Doppler OCT-measured CBF confirms the conservation of flow at branching vessels. In addition, this study demonstrated that Doppler OCT flow values correlate with hydrogen clearance flow values when both are measured simultaneously. These data validated Doppler OCT as a noninvasive quantitative method to measure tissue perfusion.
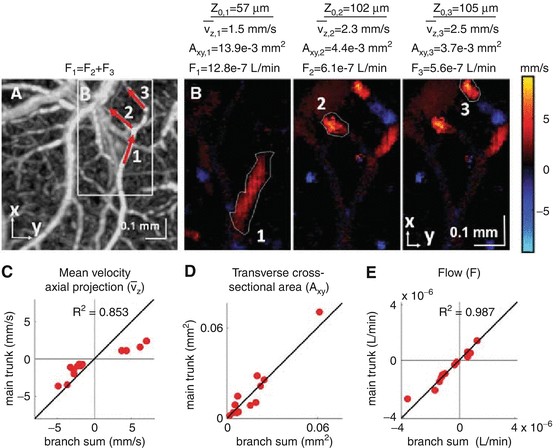

Fig. 66.2
Conservation of Doppler OCT-measured CBF at branch points in a thinned rat skull preparation. (a) OCT angiogram showing three locations in a branching vessel. (b) En face Doppler OCT images, presenting the axial flow velocity, at two depths corresponding to the main trunk location (1) and two branch locations (2, 3) shown in panel A. Plots of mean axial velocity (c), transverse cross-sectional area (d), and flow (e) in the main trunk and summed over branches in 13 branching vessels are shown (Reprinted from [13] with permission)
66.2.2 Dynamic Light Scattering Optical Coherence Tomography (DLS-OCT)
While Doppler OCT generally measures the axial component of CBF velocity, a recently proposed method integrating OCT with dynamic light scattering (DLS) analysis enables measurement of the transverse component of flow velocity independently of and simultaneously with the axial velocity. This section provides a technical description of the integration, DLS-OCT, and the next section discusses its application to brain cortex imaging. DLS is widely used to quantify the dynamics of scattering particles by analyzing the autocorrelation function of light scattered from the particles, enabling an analysis of the particles’ diffusion and/or flow velocity [14–16]. Integration of DLS with OCT will provide μm-resolution 3-D imaging of heterogeneous diffusion and flow but requires a suitable DLS theory [17–22] for accurate implementation. Recently, Lee et al. proposed such a DLS theory by deriving the field autocorrelation function directly from the complex-valued OCT signal and validated DLS-OCT measurement of diffusion and flow through phantom experiments [23].
Dynamic OCT imaging of a sample produces four-dimensional (space and time) data of the complex-valued reflectivity, R(r, t). The field autocorrelation function is obtained as
![$$ g\left(\mathbf{r},\tau \right)=E\left[\frac{{\left\langle {R}^{*}\left(\mathbf{r},t\right)\;R\left(\mathbf{r},t+\tau \right)\right\rangle}_t}{{\left\langle {R}^{*}\left(\mathbf{r},t\right)\;R\left(\mathbf{r},t\right)\right\rangle}_t}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_68_Chapter_Equ1.gif)
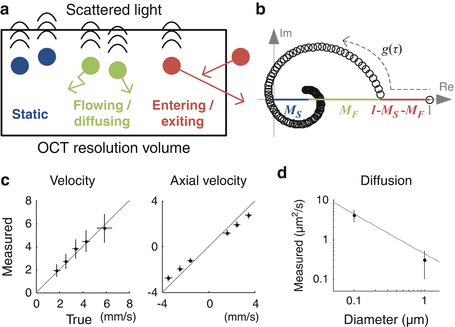
where * denotes the complex conjugate, < > t indicates an average over time, and E[ ] means the average over initial positions of the scatterers. When static and moving particles are mixed in the OCT probing volume and the moving particles can exhibit either translational or diffusive motion (Fig. 66.3a), the OCT signal can be expressed by

where q is the representative scattering vector and h is the inverse of voxel size. The scattering cross sections of the particles are considered to be similar. Detailed descriptions of the other quantities and assumptions are given in [23]. The movement of a particle can be expressed by the self-interaction term of the Van Hove space-time correlation function [24], that is, the probability that the particle which was initially at position r i at time t i is found at position r f at time t f , P 1(r f , t f |r i , t i ). The probability of a particle exhibiting both translational and diffusive motions with the velocity v and the diffusion coefficient D can be formulated by
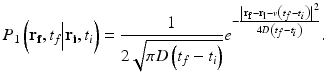
![$$ g\left(\mathbf{r},\tau \right)=E\left[\frac{{\left\langle {R}^{*}\left(\mathbf{r},t\right)\;R\left(\mathbf{r},t+\tau \right)\right\rangle}_t}{{\left\langle {R}^{*}\left(\mathbf{r},t\right)\;R\left(\mathbf{r},t\right)\right\rangle}_t}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_68_Chapter_Equ1.gif)
(66.1)

(66.2)
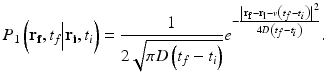
(66.3)

Fig. 66.3
Theory and validation of DLS-OCT. (a) Particles within the OCT resolution volume can be categorized into three groups: static, flowing or diffusing, and entering or exiting particles. For clarification, entering/exiting particles enter into or exit out of the voxel during a single measurement time step, resulting in stochastic fluctuations of the OCT signal. (b) The general behavior of the field autocorrelation function in the complex plane predicted by DLS-OCT theory. M S and M F are approximately proportional to the fractions of static and flowing/diffusing particles, respectively, weighted by their scattering cross sections. It adequately explained the measured ones. (c) Phantom validation of DLS-OCT measurement of the flow velocity using a piezoelectrical sample with controlled velocity. The velocity (left) means the absolute velocity, (v t 2 + v z 2)1/2. (d) Phantom validation of DLS-OCT measurement of the diffusion coefficient using microsphere samples with different diameters. The gray line shows the Einstein-Stroke equation (Reprinted from [23] with permission)
Then, the field autocorrelation function of the OCT signal (Eq. 66.2) whose r F (t) and z F (t) satisfy Eq. 66.3 was obtained as
![$$ g\left(\mathbf{r},\tau \right)={M}_S\left(\mathbf{r}\right)+{M}_F\left(\mathbf{r}\right)\;{e}^{-{h}_t^2{v}_t^2\left(\mathbf{r}\right){\tau}^2-{h}^2{v}_z^2\left(\mathbf{r}\right){\tau}^2}{e}^{-{q}^2D\left(\mathbf{r}\right)\tau }{e}^{iq{v}_z\left(\mathbf{r}\right)\tau }+\left[1-{M}_S\left(\mathbf{r}\right)-{M}_F\left(\mathbf{r}\right)\right]\delta \left(\tau \right) $$](/wp-content/uploads/2017/03/A76297_2_En_68_Chapter_Equ4.gif)
where M S (r), M F (r), v t (r), v z (r), and D(r) are the parameters of particle dynamics to be estimated for each position while the others are the parameters given by the measurement system. M S is the fraction of the static particles, M F is the fraction of the moving particles, v t is the transverse component of the flow velocity, v z is the axial component, and D is the effective diffusion coefficient quantifying the diffusive motion of particles as in Eq. 66.3. This autocorrelation function adequately explained the general behavior of the experimental measurements (Fig. 66.3b).
![$$ g\left(\mathbf{r},\tau \right)={M}_S\left(\mathbf{r}\right)+{M}_F\left(\mathbf{r}\right)\;{e}^{-{h}_t^2{v}_t^2\left(\mathbf{r}\right){\tau}^2-{h}^2{v}_z^2\left(\mathbf{r}\right){\tau}^2}{e}^{-{q}^2D\left(\mathbf{r}\right)\tau }{e}^{iq{v}_z\left(\mathbf{r}\right)\tau }+\left[1-{M}_S\left(\mathbf{r}\right)-{M}_F\left(\mathbf{r}\right)\right]\delta \left(\tau \right) $$](/wp-content/uploads/2017/03/A76297_2_En_68_Chapter_Equ4.gif)
(66.4)
Phantom experiments validated DLS-OCT measurement of the flow velocity and diffusion (Fig. 66.3c). For the velocity measurement, a piezoelectrically actuated static sample was used to simulate axial movements of particles while transverse movements were implemented by galvanometric lateral scanning of the OCT beam. The absolute and axial velocities were reliably measured across various true values of the flow velocity and angle. Microsphere samples of 0.1 and 1 μm in diameter were used for validating the diffusion measurement. The measured diffusion coefficient agreed with the theoretical values given by the Einstein-Stokes equation. The diffusion coefficient was estimated to be sufficiently small in the velocity phantom experiment, while the diffusion phantom experiment resulted in negligible velocities. These results confirmed that DLS-OCT can effectively distinguish whether the motion is translational or diffusive and accurately measure either the flow velocity or the diffusion coefficient.
66.2.3 DLS-OCT Imaging of CBF Velocity
Based on the validated DLS-OCT measurement of the flow velocity and diffusion coefficient, DLS-OCT imaging of the living rodent cortex was performed. A-scans were repeated 100 times over ∼2 ms at a fixed position, and the position was moved in a raster manner to scan the volume of interest of the cortex. The 4D (space and time) complex-valued field reflectivity of the sample was obtained and then was used to produce the 4D (space and time lag) autocorrelation function data. Analysis of the 4D autocorrelation function data led to 3-D maps of the transverse and axial velocities, the diffusion coefficient, and the coefficient of determination (R 2).
As shown in Fig. 66.4a, the absolute velocity map clearly revealed the structure of the vascular anatomy and cerebral blood flow. The axial velocity map showed the axial component of the flow velocity, which looked very similar to conventional Doppler OCT images (e.g., Fig. 66.1c). The flow direction determined by the axial and transverse velocities agreed with the structural direction of vessels (Fig. 66.4a, right).
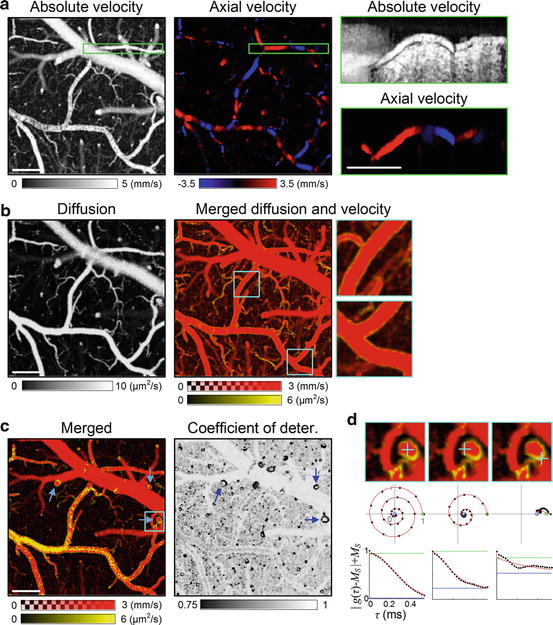

Fig. 66.4
DLS-OCT imaging of the brain cortex in a rat thinned skull preparation. (a) The first image presents the maximum projection (MP) of the 3-D map of the absolute velocity along the depth (i.e., en face), and the second image presents the en face signed maximum projection (SMP) of the 3-D map of the axial velocity. The images with the green boundary show the MP of absolute velocity and the SMP of the axial velocity along the transverse direction (i.e., cross-sectional) over the volume indicated as the green box in the en face images. The SMPs of the axial velocity are presented over the range from –5/√2 to 5/√2 mm/s, where a negative velocity (blue color) means that blood flows toward the surface of the cortex. (b) The first image presents the en face MP of the 3-D map of the diffusion coefficient. In the second image, the diffusion image (yellow) is overlaid with the absolute velocity image (red). The 3× magnified images of the cyan boxes are presented to clearly show the characteristic dynamics of the vessel boundaries. This merged image is presented with smaller ranges of the velocity and diffusion coefficient for higher contrast. (c) Single planes of the merged map and the coefficient of determination map at a depth of 120 μm are presented. (d) Examples of the autocorrelation function are presented for three voxels (cyan crosses) that are located in the plane indicated as the cyan box in (C). The middle row shows the autocorrelation function data (black dots) and their fits (red lines) in the complex plane, where the estimated M S and M S + M F are presented as the blue and green circles, respectively. The bottom row shows decay of the M F -terms. The coefficients of determination of these three voxels are R 2 = 0.999, 0.988, and 0.647. All scale bars, 100 μm (Reprinted from [23] with permission)
When the diffusion map is overlaid with the absolute velocity map (Fig. 66.4b), high-diffusion and low-velocity voxels were observed at the boundary of vessels. Interestingly, the vessel boundaries also exhibited a characteristic low coefficient of determination (Fig. 66.4c). Single-plane images without projection clearly showed the result that the vessel boundaries exhibit high diffusion, low velocity, and low R 2. At the circular cross-sections of the vessels (Fig. 66.4c, blue arrows), high-velocity and high-R 2 blood flow are surrounded by the high-diffusion, low-velocity, and low-R 2 dynamics of the vessel boundaries. In particular, the low R 2 means that the motion was neither translational nor diffusive; it might be oscillatory due to the interaction between blood flow and the tension of the vessel walls.
In addition to CBF imaging, DLS-OCT maps revealed another interesting dynamic occurring in the brain cortex. Along with high-NA OCT structural imaging, which identifies neuronal cell bodies in its minimum intensity projection (Fig. 66.5, MinIP; [25]), high-NA DLS-OCT imaging was performed on the cortex. The diffusion map revealed high-diffusion spots in the nonvascular area. They are different from vessel boundaries in that they showed high R 2 whereas the vessel walls exhibited the characteristic low R 2 values. Therefore, another map was introduced to represent diffusion masked with high R 2 (R 2 > 0.998, green color in Fig. 66.5). These high-diffusion high-R 2 green spots were morphologically confined when viewed in 3-D, whereas the high diffusion observed at vessel walls extended over a vascular segment. The positions of the green spots were highly correlated with those of neuronal cell bodies. Meanwhile, the green spots generally did not fill the whole area of cell bodies (e.g., Fig. 66.5b). Some of their morphology (e.g., the first three in Fig. 66.5b, where green spots surround a smaller dark sphere), was quite similar to those of intracellular motility in the cytoplasm observed in a high-resolution in vitro imaging study [26]. The mean diffusion as a function of the distance from the nucleic center also showed that the peak diffusion did not locate at the center of cell bodies (Fig. 66.5c). These results on morphology suggest that the green spots are distributed over the space surrounding nuclei, likely in the cytoplasm. Finally, the diffusion coefficient of the spots agrees with those of the motion of intracellular organelles measured in vitro [27–29]. Therefore, the green spots likely represent the diffusion-like movements of intracellular organelles.
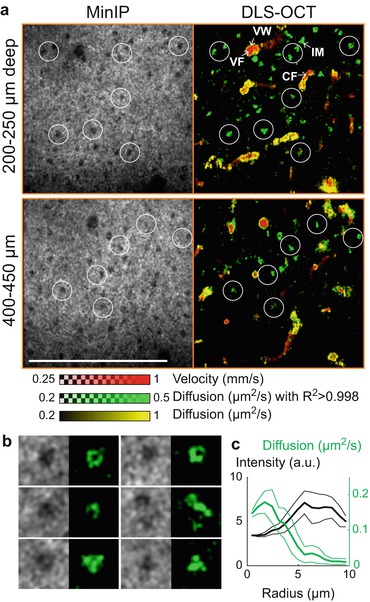

Fig. 66.5
DLS-OCT imaging of neuronal intracellular motility. (a) High-NA DLS-OCT imaging of the brain cortex. The velocity and diffusion images (red and yellow) are superimposed with the map of diffusion with high R 2 (green). White circles are collocated to visually guide the spatial correlation between the positions of neuronal cell bodies (dark spots in MinIP) and neuronal IM (green spots). Not all cell bodies are marked. VF vessel flow, CF capillary flow, and VW vessel wall. The small range of the diffusion coefficient is used to increase the image contrast. Scale bar, 200 μm. (b) Several examples of neuronal nuclei observed in MinIP and neuronal IM observed in the high-R 2 diffusion map. Image size, 25 × 25 μm, for each. (c) The mean intensity (black) and diffusion (green) as the function of the distance from the nucleic centers (n = 10) (Data are presented in mean ± SD) (Reprinted from [94] with permission)
66.3 OCT Imaging of Hemodynamic Responses: Second-Timescale Transient Dynamics
As described in the Introduction, when the brain is activated, additional oxygen and glucose should be supplied via increased blood flow in association with spatiotemporally varying metabolic needs. Neurovascular coupling represents the current paradigm for understanding this energy supply regulation of the brain. This current paradigm focuses on how local neuronal activity adjusts arteriolar tone (and thus local CBF) in association with metabolic needs ([30] for review). A number of studies have discovered a range of mechanisms underlying this coupling. Neurotransmitter-mediated signaling from neurons and astrocytes to vascular smooth muscles that dilate and constrict arterioles plays a major role in regulating CBF [31, 32]. When this energy supply regulation does not work, neurons and glia become injured or die. Since such an inadequate supply occurs in various disorders of the brain, understanding the mechanisms is a prerequisite for developing therapies to correct defects in blood flow control occurring in stroke [33], hypertension [34], and Alzheimer’s disease [33]. This section describes how OCT can advance in vivo imaging of neurovascular coupling. This section introduces studies that used OCT for imaging of such neurovascular coupling.
The current paradigm has recently been challenged by the concept that capillaries also contribute to blood flow regulation in response to neuronal activity, so-called neuro-capillary coupling. This concept is supported by recent studies showing that contractile cells called pericytes can control the diameter of capillaries [35], and substances altering the arteriole diameter can contract and relax pericytes as well [36], likely due to alteration of the intracellular Ca2+ concentration of pericytes [37]. For example, pericytes (and thus capillaries) constrict in response to noradrenaline and dilate in response to glutamate in brain slices [35]. Extending our knowledge of blood flow dynamics down to the capillary level will be helpful as the capillary bed works as a direct interface through which oxygen and glucose are supplied to the tissue. Regulation of blood flow at the capillary level, however, has been only demonstrated either in vitro or in pathological conditions [38, 39]. Capillary flow regulation in response to neural activation has yet to be demonstrated in vivo under physiological conditions [40], but this is advancing rapidly. Furthermore, there are controversial reports on the in vivo capillary flow responses. Being different from arterioles, capillaries have been reported to exhibit highly heterogeneous responses to neural activation [41, 42] and even nearly stochastic distributions during baseline [43], potentially masking neural activity-induced responses of single capillaries [44].
Due to the nature of capillary flow responses, demonstrating neuro-capillary coupling in vivo requires systematic measurement of blood flow over a reasonably large number of capillaries at the same time. To date, capillary flow responses have been measured by tracking fluorescence-labeled single RBCs with either video microscopy (VM) [43] or two-photon microscopy (TPM) [41, 45]. Those techniques, however, are generally not suitable for the systematic measurement of large numbers of capillaries since they measure the responses over only several capillaries within a single focal plane (VM) or capillary by capillary (TPM). Meanwhile, OCT generally enables a larger imaging volume per time, but the existing OCT-based technologies, including Doppler OCT and DLS-OCT described in the previous section, are still far from achieving the target number of capillaries (>100) with sufficient temporal resolution (∼1 s) as they require many consecutive scans per position to estimate the flow speed [23, 46, 47]. This section introduces another OCT-based technology for measurement of flow speed and its application to high-speed volumetric imaging of blood flow speed over hundreds of capillaries at the same time.
66.3.1 Slow Changes in the OCT Signal Associated with Neural Activation
Intrinsic optical signal (IOS) generally images oxygenated and deoxygenated hemoglobin concentration at the surface of cortex. Therefore, it can image hemodynamic responses to neural activation while providing two-dimensional, depth-integrated activation maps of brain activity. Whereas general IOS imaging does not provide depth-dependent information of the hemodynamic response, OCT can measure the depth profile of neurovascular coupling. Chen et al. [48] performed IOS imaging to identify an activated region of rat somatosensory cortex during forepaw electrical stimulation and repeated OCT B-scans on the activated and control regions (Fig. 66.6a), resulting in 3-D (x,z,t) OCT data. At every voxel, a temporal fractional change in the OCT intensity signal was obtained with respect to its baseline. This functional OCT signal was significantly larger in the activated region (Figs. 66.6b, c). The mean of the functional OCT signals exhibits time courses similar to that of IOS, with a net positive change that occurs during the activation period (Fig. 66.6d). When the OCT signal is integrated over depth, its lateral profile was highly correlated with that of IOS, supporting that the OCT signals represent hemodynamic responses to neural activation. These OCT signals revealed a laminar profile of hemodynamic responses that a deeper area responds earlier than a superficial area (Fig. 66.6e). This is consistent with the fact that the neuronal activity initiates in the deeper layers of the cortex and then propagates to the superficial cortex. While the neural propagation occurs over only 10’s of milliseconds, the delay in the vascular response is 100’s of milliseconds. The greater delay in the vascular response indicates intriguing laminar differences in neurovascular coupling that requires further study. These laminar OCT results were recently elucidated further in [49].

Fig. 66.6
IOS and OCT imaging of brain activation. (a) Localization of activation area in IOS imaging. Two OCT scans are denoted by arrows 1 (red) and 2 (black). (b) Cross-sectional map of fractional changes in the OCT intensity at time window 4–6 s over the activation region denoted by the arrow 1 during the stimulation of the contralateral forepaw. (c) Functional OCT image at time window 4–6 s over the scan denoted by arrow 2. (D) Plots of positive, negative, and summation OCT signals at regions with significance level α < 0.001. The time course of IOS signal (×10) is also included to show the temporal correspondence. (e) Plot of the averaged time lags at the same depth (from the skull surface) versus the depth. Two distinct regions are indicated by different slopes (S1 and S2) (Reprinted from [48] with permission)
66.3.2 Quantitative OCT Imaging of Hemodynamic Responses
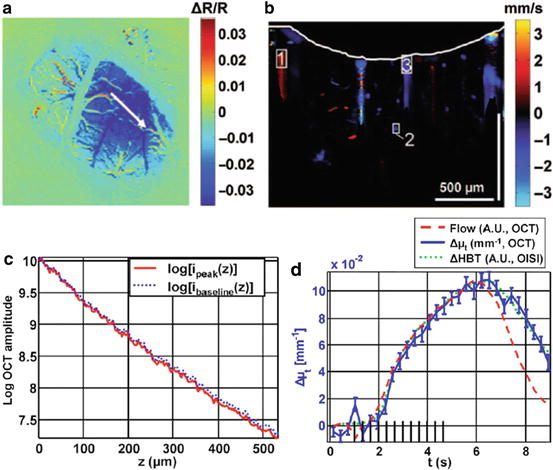
The above study showed OCT signal changes in response to neuronal activity that were similar to the hemodynamic responses measured by IOS imaging, but it remains unclear what mechanisms are driving those OCT signal changes. Srinivasan et al. measured brain activation-evoked changes in blood flow and total hemoglobin in the rat somatosensory cortex [50]. They performed IOS imaging to identify the activated region and chose an OCT scanning line (Fig. 66.7a). Then, Doppler OCT imaging was performed during somatosensory activation for measuring fractional changes in blood flow (Fig. 66.7b for baseline, Fig. 66.7d for flow in the draining vein). In addition, activation-induced changes in the extinction coefficient were measured to estimate dynamics of the total hemoglobin concentration (Fig. 66.7c). Assuming single scattering, the OCT signal profile R(z,t) is determined by the extinction coefficient μ t (t) and the backscattering A(t), which are time-varying variables due to brain activation. Using this relation, a least-squares fit was performed to determine Δμ t (t) as shown in Fig. 66.7d (blue). As a result, the time course of Δμ t was nearly identical to that of ΔHbT measured by IOS, supporting that the OCT extinction coefficient changes over time were closely related to changes in the total hemoglobin concentration. In contrast, the Doppler OCT-measured flow response showed a faster relaxation than both the ΔHbT and Δμ t responses, which is consistent with the well-known delayed recovery in cerebral blood volume [51].