(29.1)
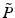(q, k) is one of the two complex conjugate terms of the interference signal, recorded as a function of wavenumber k in spectrometer-based or swept-source OCT, and lateral spatial frequency q. q is obtained by inverse Fourier transformation of the signal along the lateral scanning position ρ. The two tildes indicate the Fourier transformation along the lateral and the axial spatial coordinates. CTF(q, s, k) is the coherent transfer function of wavenumber k, depending on all spatial frequencies [25]. A(k) is the power spectral density of the light source, which is weighted by the wavenumber k, a remnant of the k 2 factor in the commonly used scattering potential k 2χ(r). The origin of the z coordinate is placed in the focal plane of the imaging optics, and the reference arm length is assumed matched to this position. An additional linear phase term would otherwise have to be added. The same formalism obviously also holds for time domain OCT, except that 
(q, k) does not directly correspond to any measured signal. Also, experimental limitations such as instantaneous coherence length, spectrometer resolution, or wavenumber linearization are ignored.The CTF is defined through the illumination and the detection optics. Indeed, both parts play an equal role in OCT. The illumination optics defines the focal volume that scans over the sample. Part of this illumination light is scattered back by the sample susceptibility and then finally filtered by the detection optics that rejects any contribution that does not match the detection mode. The concept of the generalized aperture is convenient to express the illumination and detection modes, as it also holds for higher NA, and could be extended to vector notation [26]. The generalized aperture describes the electromagnetic field in the focal volume as the three-dimensional Fourier transformation of its plane wave decomposition. These components lie, by definition, on a spherical shell of radius k, and their angular distribution corresponds, within the limits of the Debye approximation, to the field distribution in the spherical output principle plane of the imaging objective with a radius corresponding to the focal length of this lens. And the radial distribution in this principle output plane corresponds, in turn, to the distribution in the flat input principle plane.
In spatial coordinates, the signal recorded for each wavenumber corresponds to the convolution in the lateral direction of the product of the illumination and the detection mode with the sample susceptibility, weighted by the power spectral density. No scanning in the axial direction is performed. The corresponding situation in the spatial frequency domain is the product of the sample spatial frequency spectrum (SSFS) with the convolution along all spatial frequencies of the illumination and detection modes, i.e., their generalized apertures, which defines the CTF. To take account of the absence of axial scanning, the integral along the axial spatial frequency s is taken to find expression (29.1). The integral along s is equivalent to a Fourier transformation back to the spatial domain, evaluated only at the position z = 0.
Hence, the CTF is defined as the convolution of the two spherical shells, m ill and m det, as represented in Fig. 29.1a:
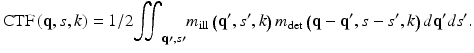
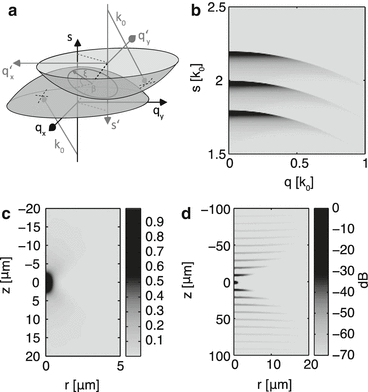
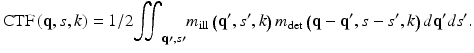
(29.2)
Fig. 29.1
(a) The convolution of the illumination and detection generalized apertures defines the CTF. (b) The CTF scales about the origin with the wavenumber. (c) The 3D FT of the CTF at a given wavenumber defines the corresponding focal volume. (d) Simulated tomogram of individual point-like scatterers aligned along the axial direction at 10 um intervals for a Gaussian illumination mode with an NA of 0.5
The field distribution on the shells is entirely defined by the illumination and detection modes at the principle input plane of the sample objective. Panel (b) of Fig. 29.1 displays the resulting CTFs for three wavenumbers for a system with Gaussian illumination and detection modes, whose waists fill 70% of the aperture of the sample objective with NA = 0.5. Due to geometry, the CTF has an outer rim defined by a sphere of radius 2k. For the Gaussian CTF, the transmission values are highest at this rim and then decay for smaller s. A change in wavenumber has the effect of scaling the CTF around the origin of the spatial frequencies with a scaling factor 2k. Due to the limited bandwidth of the light sources used, usually limited to less than one fifth of the central wavenumber, it is possible to ignore this scaling effect and simply assume that the CTF at a given wavenumber is a shifted copy of the CTF at the central wavenumber CTF(q, s, k) ≈ CTF(q, s, k c ) ⊗ δ(s − 2(k − k c )). As usual, to reconstruct the tomogram, the inverse Fourier transformation from k to z is computed:
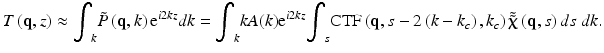
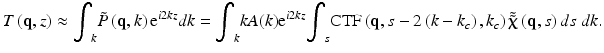
(29.3)
In this view, the tomogram can be pictured as the Fourier transform of the SSFS convolved with the central wavenumber CTF along s and weighted with the power spectral density of the employed light source. Panel (c) of Fig. 29.1 displays the focal volume corresponding to the central wavenumber’s CTF. And panel (d) represents the tomogram of point-like scatterers, aligned along the axial direction at 10 μm intervals. This clearly illustrates the limited depth of field for a CTF with such a high NA. Only a single in focus scatterer appears clearly resolved. The signal of the out of focus scatterers drops rapidly in intensity and is blurred in the lateral direction. Although the coherence gating still works and clearly locates the signal at a single depth, this depth changes with the lateral scanning position.
Having revealed how the CTF impacts the final tomogram, it is possible to devise an ideal CTF: It should be separable along q and s, approach a Dirac function along the axial spatial frequency, and feature a smooth envelope along the lateral spatial frequencies. Along the axial spatial frequency, the CTF acts as the sampling function of the Fourier domain detection, mapping an axial spatial frequency to a specific wavenumber. The range of this mapping is imposed by the spectral bandwidth and defines the resulting axial resolution. In the lateral direction, the envelope of the CTF simply apodizes the higher lateral spatial frequencies, defining the lateral resolution.
This hypothetical situation of this idealized CTF is depicted in Fig. 29.2a, d and results in the expected ideal tomogram. A real CTF usually differs in two ways from this ideal CTF: Its width along s and the separability of the CTF along q and s. Most CTFs exhibit a curved shape, making the position of the window along s dependent on q. Figure 29.2b, e demonstrate the effect of a hypothetical CTF that still consists of two separable windows along q and s, but with an increased window width along s. Although the signal of the out of focus scatterers does not experience any blurring, their signal intensity drops rapidly with increasing out of focus distance. On the other hand, panels (c) and (f) show the effect of a very narrow window along s, but with a spherical curvature along q. In this case, defocused scatterers become extremely blurred. The integrated intensity over the blurs of the scatterers does not decrease with out of focus distance; it is simply spread over a larger area. The on axis signal, however, decreases at the same rate as in case of the previous CTF of Fig. 29.2b.
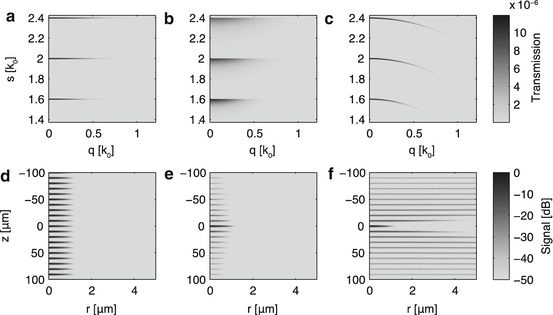
Fig. 29.2
(a) Hypothetical ideal CTF with very narrow support along s and no curvature. (b) Hypothetical CTF without curvature but finite support along s. (c) Hypothetical CTF with narrow support, but curvature. (d–f) Simulated tomograms of point-like scatterers resulting from the CTFs in (a–c)
The defocusing mechanism can be understood by recognizing that the axial position of the scatterer location translates to a phase slope in the spatial frequency domain, for all but the in focus signals. Although the SSFS amplitude of a small scattering component can be assumed nearly constant over the spatial frequency range covered by the CTF, the curved shape of the CTF results in a sampling of nonconstant axial spatial frequencies, and hence a spherical phase term, responsible for the observed blurring. ISAM [27] attempts to numerically compensate for this second effect by resampling the recorded signal in the spatial frequency domain.
If, instead of imaging individual scatterers, a tissue-like sample with many scatterers, spaced on a subresolution scale, were measured, a speckle pattern would result. In this case, the CTF of Fig. 29.2b would still result in a similar intensity decay as already observed for the single scatterers. The CTF of Fig. 29.2c, however, would result in constant signal intensity along depth. Although the resolution is lost, the signal energy is not. As is well known, speckle is resistant to defocusing.
This suggests the definition of two independent measures for the DOF: the first related to the width of the CTF along s, limiting the signal energy of out of focus structure, and the second related to the curvature of the CTF, resulting in a blurring of out of focus structure.
The CTFs depicted in Fig. 29.2 are hypothetical and cannot be engineered in practice. Certainly, a very low NA system approaches the ideal CTF, but limits the achievable lateral resolution. Striving for higher NA, the definition of the CTF as the convolution of the illumination and detection aperture severely constrains the solution space of realizable CTFs. With identical Gaussian-like illumination and detection modes, the curvature and the s-width of the CTF are directly linked and provide an identical definition of DOF. Using decoupled illumination and detection apertures provides more flexibility in engineering of a CTF, and the two criteria for the DOF will in general differ. Besides the two DOF criteria, it is also important to consider the third criterion of an ideal CTF: its lateral envelope, which should be wide and smooth to provide high lateral resolution without imaging artifacts.
29.3 Contrast and Contrast Enhancement
Imaging a scattering, semitransparent, three-dimensional object with a low coherent imaging system such as OCT and OCM is best described in terms of spatial frequencies and the concept of the CTF (see preceding section). Ignoring for the current discussion the limitations imposed on the depth of field and restricting the reasoning to the in focus region, Eq. 29.1 can be further simplified to
where sCTF is in principle the envelope of the CTF along q or more precisely its projection along s:
(29.4)
(29.5)
In this case, OCM imaging reduces to a linear, shift-invariant system and can be described in Fourier space as a filtering process. In the spatial frequency domain, the sample or object spectrum is directly related to the image spectrum, simply weighted by this filter function.
Defined by the NA of the sample lens, the sCTF has an upper cutoff qcutoff. The inverse Fourier transform of the sCTF defines the lateral PSF, and depending on the precise shape of the sCTF, the exact width of the PSF can vary.
In the axial direction, the resolution is entirely defined by the coherence length, i.e., the spectral span of the light source in the spatial frequency space. Along the axial direction, an OCM system always acts as a band-pass system, transmitting only the axial spatial frequencies in the band accessible by the light source, stretching from s = 2k min to s = 2k max, where k min and k max are the minimum and maximum wavenumbers of the light source. Only object structure with axial spatial frequencies in that range can be imaged by OCM.
Besides spatial resolution, high contrast is of paramount importance for the visual impression of a tomogram. In terms of pure spatial frequencies, the contrast can be directly defined as the visibility of the image of a pure spatial frequency, i.e., a sinusoidal variation of the square of the refractive index along a defined direction, which is entirely defined through Eq. 29.4 by kA(k) and sCTF(q).
More relevant in an experimental image is the contrast between various structures within the tissue. Figure 29.3a shows a schematic object spectrum, indicating different spatial frequency bands. The low frequency band is dominated by specular reflection (s-band). This contribution is caused by surface reflections, glass slides supporting cell samples, or other well-defined interfaces perpendicular to the optical axis. Such interfaces have a very broad axial spatial frequency spectrum (along s) mainly determined by the coherence length, but very low lateral spatial frequencies (q).
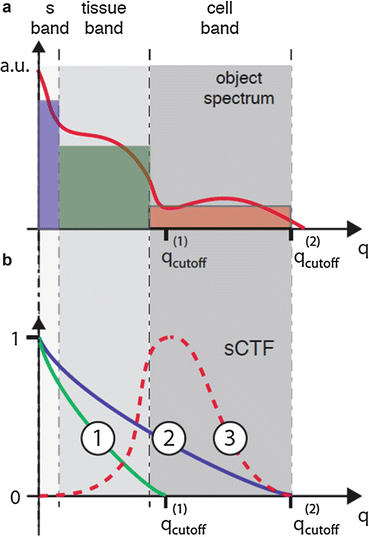
Fig. 29.3
(a) Object spectrum overlayed with the integral signal per k-band. (b) sCTF of a low NA OCM system (1), a high NA OCM system (2), and a dark field OCM (3) with identical NA as system (2)
The adjacent frequency band (tissue band) contains the macroscopic features of tissue morphology. The higher frequency (cell band) contains information of the subcellular structures. Figure 29.3b shows the sCTF of the instrumental counterpart. The diagram indicates several cases: First, the sCTF of a low NA imaging system, with a low cutoff frequency q(1) cutoff, i.e., a moderate lateral resolution; second, the sCTF of a higher NA OCM system with an increased cutoff frequency q(2) cutoff, i.e., an improved lateral resolution; and third, the sCTF of a dark field OCM system with an identical NA (when compared to the high NA OCM system), but suppressed lower spatial frequencies. This dfOCM system prevents the specular frequency band from being detected and privileges the structural bands.
Assuming two types of tissue, that both have similar spectra in the tissue band, but one of them has far more content in the cell band, would be imaged with varying contrasts with these three imaging systems. The low NA system would hardly be able to tell them apart. The higher NA system would provide sufficient contrast to distinguish the two, but only the dark field configuration would really allow a stronger differentiation of cell structures, i.e., resulting in a further contrast enhancement for all signal content in the cell band.
The integral contributions over different spectral bands are indicated by the boxes in Fig. 29.3a. A targeted selection of these contributions translates into an intrinsic contrast enhancement, an important feature in OCM especially when aiming for structural and dynamic cell imaging.
The schematic and qualitative classification of the object spectrum into different frequency bands can be substantiated for instance with works by Schmitt et al. [28], who measured the power spectrum of index variations of biological tissue by analyzing light scattered by cell samples. The cell-associated index variations follow a power-law and show a fractal index structure within a particular band of spatial frequencies. These findings have been advanced in further studies [29, 30] indicating a fractal order for light scattering in cell clusters over a large span of spatial frequencies.
In OCM the generation of adequate contrast is as important as providing sufficient resolution when imaging small features of a specimen. Imaging almost transparent cells that only slightly differ from their surrounding in their refractive index, their absorbance, or the amount and polarization of the light they scatter increases the request for enhanced or specifically tailored contrast. This demand becomes even more challenging for the observation of dynamic cell processes.
Besides the contrast between different tissues or structure, the sensitivity Σ, the signal-to-noise ratio (SNR), and the dynamic range (DR) are important key factors. The SNR is given as a ratio between the signal and the sum of all noise contributions. The sensitivity is defined as the reciprocal of the smallest reflectivity that can be resolved. The SNR and the sensitivity are principally defined through the noise present in the system. The absolute value of the CTF has, however, likewise an influence. It acts as a filter that reduces the signal and, thus, can limit these characteristics. A sensitivity of 100 dB is typical for a well-designed OCM system which for a SNR = 1 corresponds to a minimum reflectivity of Rsmin = 10−10.
However the available dynamic range is limited well below the sensitivity of an OCM system.
In spectrometer-based FDOCT the signal contains a strong DC (reference) and weaker AC (interference) contribution. For a single line detector with N discretization levels and the DC part γ filling a major part of the quantum well capacity, only a minor part α of the full well capacity is available for the interference signal.
At the saturation level of the detector, the strongest possible signal α is given by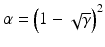 
. Neglecting all noise contributions and an interference amplitude of 
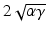, we obtain for the dynamic range DR
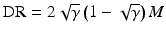
where the smallest interference contribution has been set to one discretization level 1/M. For a typical setting with γ = 0.75 and M = 2,048 (11 bits), the resulting DR is typically 50 dB.
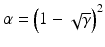. Neglecting all noise contributions and an interference amplitude of 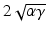, we obtain for the dynamic range DR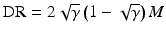(29.6)
This argument is of paramount importance when detecting small signals next to very strong signals originating from specular reflection. To avoid the detection from saturating, the reference signal frequently has to be reduced at the cost of sensitivity. In dfOCM, the specular reflections are sufficiently suppressed to maximize system sensitivity and use the available dynamic range for detection of the small scattering signal of the sample (see Fig. 29.3c).
In swept-source systems, the commonly employed dual-balanced receivers improve the DR, but specular reflections maintain the capability to saturate the detection.
The issue of low frequency band suppression with dark field configuration is nicely demonstrated in Fig. 29.4a, b. Figure 29.4a is obtained with a standard OCT system and shows an en face intensity image of a USAF resolution test target. As expected, highly reflective lines appear bright, and low reflective areas are dark. Figure 29.4b on the other hand is obtained with a dark field OCT configuration (see Sect. 29.4.3). The resulting image is obviously a band-pass filtered version of the resolution test target pattern. Interestingly, the contrast of the small numbers labeling the test patterns, which presumably have a relatively broad frequency content, appears much enhanced in the dark field image.
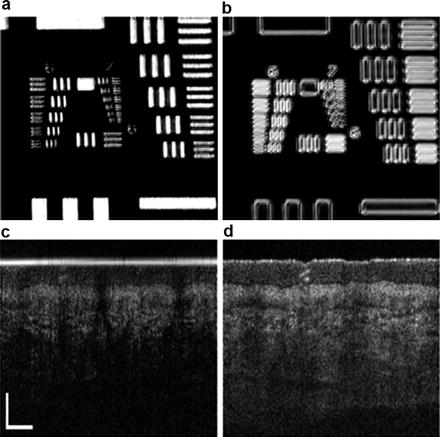
Fig. 29.4
(a–b) En face projections of a USAF resolution test target obtained with standard OCT and the xfOCT system, respectively, displaying the dark field effect. (c–d) Tomograms from skin with a glass plate on top. The glass surface is almost perpendicular to the optical axis, with the reference power adjusted to avoid saturation. Standard OCT in (c) is missing sensitivity due to the strong reflex from the glass interface. xfOCT in contrast does not suffer from the reflection and exhibits thus better sensitivity and depth penetration for the skin structures. Scale bar denotes 250 μm [57]
Figure 29.4c, d demonstrates the effect of efficient exploitation of the system dynamic range for the structural signal, when using a dark field system. In this case the sample is skin, covered by a glass plate commonly applied for better stabilization. Again Fig. 29.4c is obtained with a standard OCT system. The strong reflex from the glass interface drives the camera load close to saturation, and only a small portion of the dynamic range is left for the structure of interest, resulting in poor contrast. The situation is different for the dark field configuration as shown in Fig. 29.4d. The reflection is suppressed, and the full dynamic range is available for the actual structure, providing excellent contrast of various tissue structures. The imaging depths are likewise enhanced, due to the combined effect of the optimized sensitivity and the extended DOF that comes in hand with the dark field effect (see Sect. 29.4).
29.4 Extended Focus Optical Coherence Microscopy: Configurations and Applications
So far we presented a general theoretical framework to understand and investigate how specific illumination and detection modes define the CTF and influence the available DOF. Further, the meaning of contrast and specific regions of interest in the sample spatial frequency spectrum were discussed. As a reminder, the goal is to design a system providing high spatial resolution in all three dimensions without compromising the parallel acquisition unique to Fourier Domain OCT. If speed is not a critical parameter, performing a confocal scan in all three dimensions will undoubtedly provide the best image quality. Here, instead, a compromise between image quality and imaging speed is pursued. The particular physics of Bessel beams makes this class of beams a strong candidate to help in such a compromise, and it is tempting to replace the conventional imaging lens with an axicon-like lens. The generalized aperture of the resulting focal spot is defined by a thin annulus. The CTF resulting from a symmetric system with identical illumination and detection modes is defined by the convolution of two such annuli. Indeed, this results in a narrow and flat CTF, approaching two of the three criteria of an ideal CTF. Unfortunately, the transmission values feature very strong variations. The CTF can be pictured as a ring of twice the diameter of the annulus of the generalized aperture and a strong, very narrow central peak, connected to the outer annulus with very low transmission values. In the tomogram, this results in very strong side lobes and a very poor imaging of edge-like structures. As discussed in the introduction, for a moderate gain of DOF, such a configuration does offer a valuable configuration with the benefit of simple physical implementation, as shown for instance by Liu et al. [21] and Lorenser et al. [22].
In the attempt of realizing a more substantial gain in DOF, decoupling of the illumination and detection aperture has shown better performance. A Bessel-like mode is still used to deliver the light into the sample and illuminate the sample with an axially extended light needle. The detection volume, however, is defined as a lower NA Gaussian mode. In the following, three specific implementations of this combination and their corresponding benefits for biological applications are discussed.
29.4.1 Extended Focus Optical Coherence Microscopy: xfOCM
This first realization of extended focus OCM (xfOCM) provided a near isotropic resolution of 1.3 μm in the lateral and 2 μm in the axial direction, over an axial range of 300 μm, corresponding to a more than tenfold increase in the DOF of a Gaussian system with identical lateral resolution. An axicon lens was used to generate a Bessel-like beam, which was relayed through a scanning system and finally projected into the sample space with a microscope objective of NA = 0.3. The decoupled detection was defined by the Gaussian-like fiber mode, relayed in a way to define an NA slightly below the illumination NA. The excellent axial resolution was achieved with an Ti:Sapphire laser centered at 800 nm. Figure 29.5 displays the schematic layout; details are provided in [12, 23].
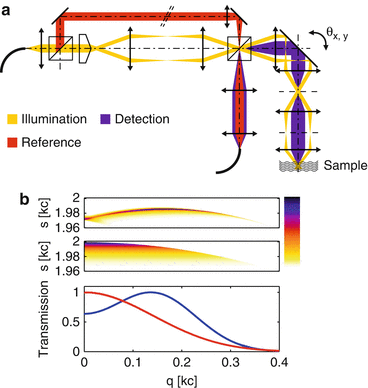
Fig. 29.5
(a) Schematic layout of the xfOCM, evidencing the decoupling of the illumination and the detection paths (not drawn to scale). (b) Top: CTF of the xfOCM configuration. Middle: CTF of a confocal Gaussian-like system with similar lateral resolution as the xfOCM. Bottom: Projections of the CTFs along s
The theoretical CTF corresponding to this configuration is shown in panel (b). For comparison, the CTF of a system with symmetric Gaussian-like illumination and detection resulting in a comparable lateral resolution is also depicted. The projections of these CTFs along s, i.e., their sCTFs, are plotted in the bottom part of the same figure. Due to the Gaussian detection, the CTF of the xfOCM configuration is curved along q and will eventually induce a defocusing for out of focus structure. Due to the Bessel-like illumination, the width of the CTF along s is very limited and provides a strong intensity signal over a significantly extended depth range. The Gaussian CTF, in contrast, features a much wider width along s, paired with a stronger curvature, resulting in a very short DOF.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
