Fig. 39.1
Comparison of (a) spontaneous Raman scattering, (b) resonant CARS, and (c) nonresonant CARS. Optical frequencies of pump, probe, Stokes, and anti-Stokes photons are related by ω as = ω p − ω s + ω pr
Conventional CARS imaging uses narrowband nanosecond or picosecond sources with frequencies tuned to selectively excite a single Raman resonance. However, this approach is limited in that the obtainable spectral information is not sufficient to discriminate between different biomolecules, or to determine their relative concentrations in unknown samples containing molecules with overlapping Raman bands. These limitations can be overcome by using a broadband Stokes pulse to cover a larger bandwidth of vibrational excitations in what is referred to as multiplex CARS [8–12]. The additional structural information made available by multiplex methods allows for quantitative molecular imaging of unknown samples. However, one disadvantage of multiplex CARS comes with the higher peak field intensities of the ultrafast broadband laser sources compared to narrowband sources, leading to a large nonresonant contribution to the overall signal due to the increased electronic response. The nonresonant CARS often dominates the collected signal and can easily mask any low-intensity resonant spectral features. The interference between the resonant and nonresonant signals poses additional problems as this leads to distortion of the retrieved Raman line shapes, which makes it difficult to measure molecular concentrations quantitatively. The presence of this undesirable nonresonant contribution has led to a variety of approaches aimed at suppressing the background signal in order to make multiplex CARS methods feasible for sensitive biomedical imaging applications [13].
The most widely used approach to suppress nonresonant CARS signal is the introduction of a local oscillator, or reference beam, for phase-sensitive interferometric detection [5, 6, 14–24]. Spectral interferometry acts to simultaneously enhance the resonant signal while eliminating the nonresonant contribution. Many variations in interferometric detection schemes have been introduced, including time-resolved interferometry [14], vibrational phase-contrast [17, 18], phase-cycling [19], and spectral-domain heterodyne CARS [6, 24]. While there are advantages to each approach, there are also significant disadvantages that can limit their applicability for quantitative high-speed imaging techniques. Time-resolved methods, such as Fourier-transform CARS [14, 15], rely on temporal scanning of the excitation pulses in order to retrieve spectral information. Likewise, phase-cycling schemes require scanning of the excitation phase to obtain the Raman spectrum [19, 20]. These methods are largely devised to overcome the constraints to spectral resolution resulting from the implementation of broadband excitation sources, but conversely impose limitations on imaging speed due to the temporal- or phase-scanning requirements. Phase-contrast CARS does not suffer these limitations and can provide much faster acquisition rates using a single-beam experimental setup [17]. However, this technique is restricted by the associated difficulties with quantitative spectral reconstruction. The most promising methods use heterodyne interferometry in a spectral-domain OCT-like scheme, which combines imaging speed, chemical sensitivity, and high spectral resolution [6, 24]. In such methods, the sensitivity increase comes from the interference of the generated CARS signal with a stable local oscillator, resulting in a possible sensitivity gain up to 1,000-fold [19]. The amplification occurs for both the resonant CARS signal and the nonresonant background, followed by the computational recovery of the phase-sensitive resonant contribution.
Nonlinear interferometric vibrational imaging (NIVI) [21] takes advantage of the speed and sensitivity of the spectral-domain detection while eliminating the dominant nonresonant background, allowing for quantitative reconstruction of Raman line shapes. This method differs from other heterodyne schemes in that spectral inteferometry enables full characterization of the CARS signal field. In the time domain, the resonant and nonresonant contributions can then be separated easily [25–27]. NIVI employs a two-pulse excitation scheme with a transform-limited Stokes pulse and a time-delayed chirped broadband pulse to probe the resonant CARS vibrational excitations. The high-resolution Raman spectrum can then be computationally reconstructed from the interferogram generated from the spectral-domain interference of the CARS signal with a reference pulse [21, 28]. This results in the amplification of the resonant component and provides quantitative molecular detection with reliable reconstruction of the Raman spectrum.
The important attributes of NIVI over other interferometric CARS-based techniques are that it simultaneously implements heterodyne amplification [29, 30], time-resolved resonant signal isolation [25], and spectral-domain interferometric field reconstruction [21]. The technique has been demonstrated in the quantitative analysis of lipid samples [31] and with molecular imaging of biological samples, including skin domains [32] and rat mammary tumor margins [33]. NIVI was capable of differentiating normal and tumor tissues with >99 % confidence and of detecting the molecular tumor margin within 100 μm. It was shown that the NIVI spectra of biomolecules are equivalent to the corresponding Raman spectra and can be acquired up to 1,000 times faster than with spontaneous Raman microscopy, at comparable signal-to-noise ratios [31, 34]. In the following sections, the theory, experimental setup, and demonstrated results of NIVI are covered in detail. Also discussed are the future directions for extending the imaging capacity of this technique into the Raman fingerprint region (500–1,800 cm−1) using ultra-broadband fiber continuum sources.
39.2 Theory
Conventional multiplex CARS measurements utilize a narrowband pump/probe pulse and a broadband Stokes pulse. However, methods using broadband pulses originating from a single femtosecond source have been devised by implementing a positively chirped pump/probe pulse [21, 28]. In doing so, the probe field is able to interact with the resonant coherent excitation over the extended vibrational time decay, whereas the nonresonant contribution due to the instantaneous electronic response only occurs for the duration of the transform-limited Stokes pulse. NIVI takes advantage of this increase in resonant CARS signal produced by the chirped excitation pulse and recovers the complex Raman spectra through an interferometric detection scheme. The resulting CARS signal has an identical chirp as the excitation pulse, and by measuring the cross-correlation of the signal with a known reference signal, the time-resolved resonant contribution can be extracted. By this method, an accurate Raman spectrum can be retrieved while eliminating the dominant nonresonant signal.
CARS is a wave-mixing process that involves the interaction of three photons to generate a fourth anti-Stokes photon at higher frequency than the incident photons. The CARS process using two broadband pulses, E p and E s , corresponding to the pump/probe and Stokes pulses, respectively, can be described in the frequency domain by the equations
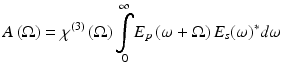
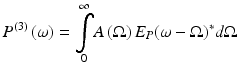
where A(Ω) is the Raman transition amplitude, χ (3) is the third-order nonlinear susceptibility of the material, P (3) is the third-order hyperpolarizability, and Ω is the resonant molecular vibrational frequency. The two equations give the two-step time evolution of a CARS process involving many possible simultaneous Raman-active vibrations. By Eq. 39.1, a molecule is put into a coherent vibrationally excited state by the pump frequency ω p and Stokes frequency ω s that are separated by the vibrational frequency Ω = ω p − ω s. Using a broadband Stokes pulse enables the simultaneous excitation of vibrational modes over a wide range of frequencies. The generation of anti-Stokes radiation is described by Eq. 39.2, in which the molecule is stimulated from the coherently excited vibrational state by the probe frequency ω 1 to produce the higher energy photon at ω AS = ω p + Ω = 2ω p − ω s. For broadband excitation, the anti-Stokes signal must be summed over all probe frequencies. The Raman response of the sample is contained in the nonlinear susceptibility, χ (3)(Ω) which contains resonant and nonresonant contributions, χ (3)(Ω) = χ NR (3) + χ R (3)(Ω).
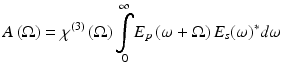
(39.1)
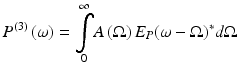
(39.2)
For CARS using a chirped pump/probe pulse, the spectrum can be expressed by the equation
![$$ {E}_p\left(\omega \right)={E}_0 \exp \left[-i{\left(\omega -{\omega}_0\right)}^2/2\alpha \right] $$](/wp-content/uploads/2017/03/A76297_2_En_40_Chapter_Equ3.gif)
where α is the chirp rate of the pulse. From the stationary phase approximation for a small α, the time-domain signal can be written as
![$$ {E}_p(t)={\alpha}^{-1/2}{E}_0\left(\alpha t+{\omega}_0\right) \exp \left[i\left(\alpha t/2+{\omega}_0\right)t\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_40_Chapter_Equ4.gif)
(39.3)
(39.4)
The Stokes pulse spectrum E S (ω) is transform limited and centered about t = 0 such that E S (ω) is real. Because of this, the instantaneous frequency of the pump/probe pulse at t = 0 is ω 0, which can be approximated as a δ function. With these representations of the pump/probe and Stokes pulses, the nonlinear polarizability expressed in Eq. 39.2 can be approximated as
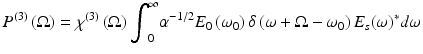
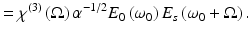
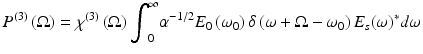
(39.5)
![$$ {E}_{AS}={\alpha}^{-1/2}{E}_0\left(\alpha t+{\omega}_0\right) \exp \left[i\left(\alpha t/2+{\omega}_0\right)t\right]\frac{1}{2\pi }{\displaystyle {\int}_0^{\infty }d\Omega}{\chi}^{(3)}\left(\Omega \right){E}_s\left({\omega}_0-\Omega \right){E}_0\left({\omega}_0\right) \exp \left(i\Omega \mathrm{t}\right). $$](/wp-content/uploads/2017/03/A76297_2_En_40_Chapter_Equ6.gif)
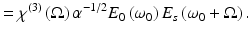
The chirp of the probe can be removed by multiplying the anti-Stokes pulse by the conjugate phase exp[−i(αt/2 + ω 0)t]. Then, the inverse Fourier transform of this product produces χ (3)(Ω), weighted by the Stokes spectrum, which is the estimation of the Raman spectrum.
NIVI is implemented experimentally by reconstructing the complex CARS field from the interferometric cross-correlation of the anti-Stokes and reference fields, retrieving amplitude and phase information of the anti-Stokes field. The interferogram is generated by mixing the CARS field with a transform-limited reference pulse. The measured interferogram, I(ω), is described by the equation
![$$ I\left(\upomega \right)={\left|{E}_{AS}\left(\upomega \right)\right|}^2+{\left|{E}_{ref}\left(\upomega \right)\right|}^2+2\mathrm{R}\mathrm{e}\left[{E}_{AS}\left(\upomega \right){E}_{ref}{\left(\upomega \right)}^{*} \exp \left(-i\upomega \tau \right)\right] $$](/wp-content/uploads/2017/03/A76297_2_En_40_Chapter_Equ7.gif)
where E AS (ω) and E ref (ω) are the anti-Stokes and reference fields, respectively, and τ is the time delay between the two pulses (Fig. 39.2a). The spectral interferogram contains DC components from the CARS and reference fields and the phase-sensitive cross-term that contains the NIVI signal. The DC reference term can be removed by the subtraction of the known reference spectrum. The remaining terms can be separated in the time domain, wherein the DC component of the CARS field can be rejected, leaving only the phase-sensitive components (Fig. 39.2b). Substituting χ(ω) = E AS (ω)E ref (ω)* and taking the inverse Fourier transform of I(ω) yields
(39.7)
(39.8)
The first term is a slowly varying DC component symmetric about t = 0, while the last two terms are time reversed from each other. As it is known that there is no CARS signal prior to the vibrational coherence induced by the Stokes pulse, the time origin can be shifted to be the center of the Stokes pulse, thereby isolating the χ(t − τ) term (Fig. 39.2c). The Fourier transform of the remaining term results in χ(ω) = χ (3)(ω)*E s (ω − Ω)E ref (ω)*. The nonresonant CARS signal is real and can be rejected by discarding the real part of χ (3). The NIVI spectrum is represented by the imaginary part of χ (3) and is analogous to the spontaneous Raman spectrum (Fig. 39.2d).
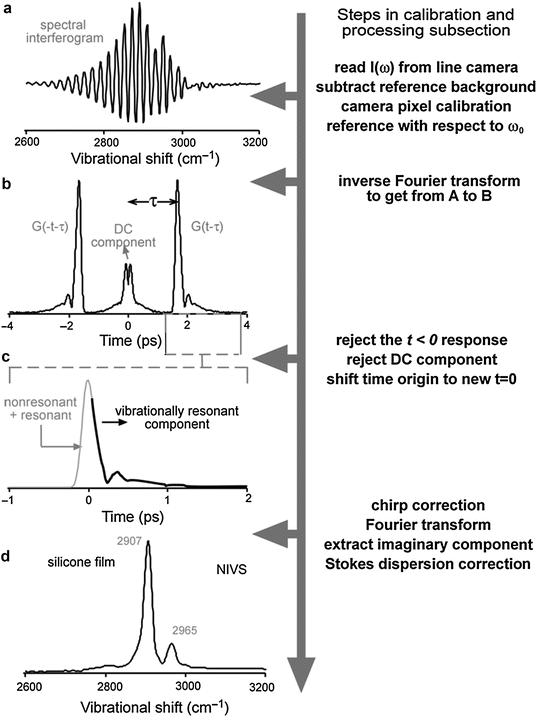
Fig. 39.2
Working principle of Fourier-transform spectral interferometry is demonstrated by extracting the NIVI spectrum of a silicone film starting from the interferogram acquired on the line camera. (a) Wavelength calibrated spectral interferogram referenced to the pump wavelength. The reference power spectrum is subtracted. (b) Modulus of the time-domain polarization obtained by inverse Fourier transforming the interferogram in (a). (c) The t > 0 response, identifying the short-time nonresonant (follows the Stokes pulse shape) and long-time resonant (vibrational dephasing) components. The temporal chirp of the pump can be corrected here. (d) NIVI spectrum of a silicone film obtained as the imaginary part by Fourier transforming the time response in (c), and Stokes dispersion is corrected (Adapted from [31], with permission)
39.3 Instrumentation
The experimental NIVI setup is shown in Fig. 39.3. A mode-locked Ti:Sa oscillator (Coherent, MIRA, 82 MHz) is used to seed a regenerative amplifier (Coherent, RegA-9000). The 380-mW, 82-MHz Ti:Sa output is amplified to 1.1 W at a 250-kHz repetition rate, resulting in microjoule pulse energies. The amplifier output is split through a 90:10 beam splitter, sending 90 % of the light to pump an optical parametric amplifier (Coherent, OPA-9450), which generates the Stokes pulse at 1,060 nm and the reference pulse at 655 nm, corresponding to the idler and signal pulses generated from the OPA, respectively. The remaining 10 % of the amplifier output is used as the probe beam. The probe pulses are linearly chirped to ∼6 ps by passing the beam through an 85-cm bar of BK7 glass. A delay line is placed in the beam path to control the temporal delay of the probe and, therefore, the instantaneous pump wavelength. The probe and Stokes beams are recombined using a dichroic mirror and delivered to the sample in a collinear geometry. The wavelengths of the pump and Stokes pulses were tuned to target the spectral range of 2,800−3,000 cm−1, corresponding to the C−H stretching vibrational region. The power of the excitation pulses varied depending on the application, i.e., higher powers are needed for imaging of biological samples, which are highly scattering and contain low concentrations of the specific target molecules.
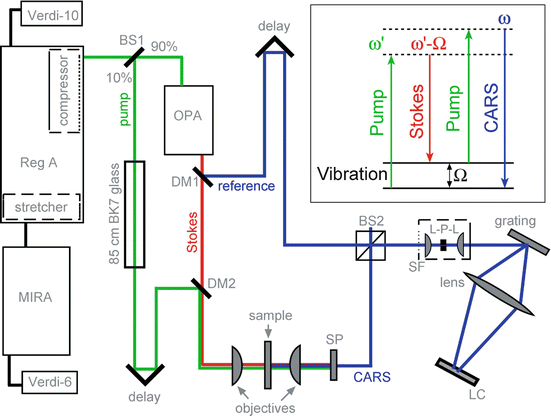
Fig. 39.3
Experimental setup for nonlinear interferometric vibrational imaging (NIVI). MIRA–Ti:sapphire oscillator; Reg A regenerative amplifier, OPA optical parametric amplifier, DM dichroic mirrors, BS beam splitter, SP short-pass filter, SF spatial filter, LC line camera (Figure adapted from [31] and used with permission)
The probe and Stokes pulses were focused onto the sample with parallel polarization using a high-NA objective. Tight focusing of these excitation beams relaxes the phase matching conditions required for four-wave-mixing processes [2]. The nonlinear interaction of the excitation fields produces the CARS signal at a higher frequency than the incident radiation. The forward-generated CARS signal is collected by a second objective. A high-pass filter is used to remove the excitation wavelengths, transmitting only the blue-shifted CARS signal. The CARS and reference beams were combined at a 50:50 cube beam splitter for collinear detection by spectral interferometry which requires precise spatial and temporal overlap. The combined beams were spatially filtered at a 30-μm pinhole to improve beam and interference quality. They were subsequently dispersed by a grating (1,200 grooves/mm), and the spectral interferogram was acquired on a 2,048-pixel line camera (DALSA P2) at a 1-kHz line rate. The implementation of spectral interferometry allows for a significant increase in image acquisition speed, signal-to-noise ratio, and signal stability.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
