Fig. 34.1
Sketch of basic PS-OCT setup. BS beam splitter, Det detector, P polarizer, PBS polarizing beam splitter, QWP quarter wave plate, RM reference mirror, SLD super luminescent diode
A broadband super luminescent diode (SLD) emits a light beam that is vertically polarized before it illuminates a Michelson interferometer. At the non-polarizing beam splitter BS, the light is split in a reference and a sample beam. The reference beam traverses a quarter wave plate QWP1 oriented at 22.5° to the vertical. After reflection at the reference mirror and back propagation through QWP1, the light is linearly polarized at 45° to the horizontal, providing equal reference power in both orthogonal polarization channels. The sample beam traverses QWP2 oriented at 45°, providing circularly polarized light to the sample. This ensures that the measured retardation of a birefringent sample is independent of its optic axis orientation. An x-y scanner and a scanning optics are used to scan the sample beam over the sample (eye/retina). After backscattering at the sample and back propagation through QWP2, the sample beam is usually in an elliptical polarization state that carries the information on the sample’s polarization characteristics. This elliptical polarization state is to be measured and analyzed.
Sample and reference beams are recombined at the interferometer beam splitter BS where they interfere. In the detection arm of the interferometer, a polarizing beam splitter PBS splits the interfering beam into two orthogonal polarization states that are measured separately by two detectors, one for the horizontal and one for the vertical polarization state. The detectors convert the light intensity into electric signals that are amplified and recorded by frame grabbers or a data acquisition board and stored in a computer.
From the interferometric signals acquired in the two channels, information on various parameters can be derived. As we will show in Sect. 34.3.2, some basic information (reflectivity, retardation) can be obtained from the amplitude of the signals while other parameters (Stokes vectors, axis orientation) require also phase information. While the access to phase information with time domain systems required either computationally extensive methods like analytic signal continuation by a Hilbert transform [41] or more complicated experimental methods like signal demodulation [29], SD OCT methods directly provide a complex valued signal by Fourier transform of the real-valued spectral intensity data. From these complex valued signals, amplitude and phase information can readily be retrieved.
34.3.2 Calculation of Polarization States and Polarization Parameters
To illustrate how the birefringent properties of a sample can be characterized by a PS-OCT system as depicted in Fig. 34.1, we will now calculate the evolution of the polarization states of the beams within the interferometer. We will use the Jones formalism [34] which is best suited for calculation of polarization states of fully polarized beams and assume that the sample is a homogenous linear retarder. The calculation follows a similar path as used in our previous work [41, 42].
The beam incident on the Michelson interferometer, after passing the polarizer, is in a linear, vertical polarization state. Its Jones vector can be written as:
(34.1)
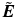is the electric field vector, with 
the scalar electric field, E 0 the field amplitude, ω the angular frequency, and t the time. The upper and lower components of the vector in Eq. 34.1 correspond to the horizontal and vertical components of the electric field vector, respectively. For the sake of simplicity, we ignore the oscillating term exp(iωt) and set E 0 = 1 in the following.The Jones vector of a beam after passing an optical element can be found by multiplying the Jones vector of the incident beam by the Jones matrix corresponding to the optical element. The Jones matrix is a 2 × 2 matrix consisting of – usually complex – elements. If more than one optical element is traversed, the input Jones vector has to be multiplied by the Jones matrices of all elements, in the order they are transmitted by the beam.
The beam described by Eq. 34.1 enters the Michelson interferometer where it is split by a non-polarizing beam splitter into a reference and a sample beam of equal field amplitudes. The reference beam passes both, the beam splitter and the quarter wave plate QWP1, twice. The effect of the beam splitter is simply to reduce the intensity of the reference beam by a factor of 2 at every pass, leading to a total intensity reduction of a factor of 4, equivalent to a reduction in field amplitude by a factor of 2. The Jones matrix of a general retarder of retardation δ and fast axis orientation θ is [43]:
![$$ \mathbf{M}\left(\delta, \theta \right)=\kern-1.2em \left[\begin{array}{cc}\hfill { \cos}^2\left(\theta \right)+{ \sin}^2\left(\theta \right)\cdot \exp \left(-i\delta \right)\hfill & \hfill \cos \left(\theta \right)\cdot \sin \left(\theta \right)\cdot \left(1- \exp \left(-i\delta \right)\right)\hfill \\ {}\hfill \cos \left(\theta \right)\cdot \sin \left(\theta \right)\cdot \left(1- \exp \left(-i\delta \right)\right)\hfill & \hfill \kern-1.2em { \cos}^2\left(\theta \right)\cdot \exp \left(-i\delta \right)+{ \sin}^2\left(\theta \right)\hfill \end{array}\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_35_Chapter_Equ2.gif)
(34.2)
For QWP1, δ = π/2 and θ = 3π/8. The Jones vector of the reference beam, after double passing QWP1 (and the beam splitter) is:
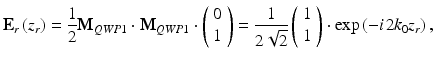
where z r is the (optical) length of the reference arm and k 0 the center wave vector of the source emission spectrum. This is a linearly polarized beam with its polarization axis oriented at 45°. It provides equal reference intensity for both, the horizontal and the vertical polarization component, which are separated by the polarizing beam splitter PBS of the detection unit. Furthermore, no phase shift occurs between the two polarization components (this would cause at least one of the vector components to have an imaginary part). Therefore, the reference beam influences neither the intensity ratio nor the phase of the interference signals recorded in the two detection channels.
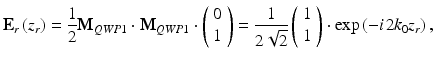
(34.3)
The sample beam passes the beam splitter QWP2 and the sample (reflectivity: R) twice each. Again, the effect of the beam splitter is simply to reduce the field amplitude by a factor of 2. QWP2 has retardation and axis values of δ = π/2 and θ = π/4, respectively. Assuming that the polarizing properties of the sample can be described by a homogenous retarder (Jones matrix M sample , retardation δ s (z), fast axis orientation θ s (constant with depth)), the Jones vector of the sample beam, after exiting the interferometer towards the detection arm, is [41, 44]:
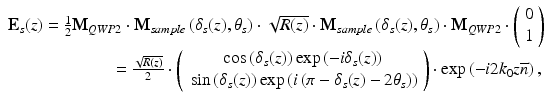
where z is the geometrical distance from the interferometer beam splitter to a sample reflection site,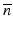 
is the mean refractive index of ordinary and extraordinary beam, and δ s (z) = Δn · z · k 0 (Δn is the refractive index difference between ordinary and extraordinary beam; for simplicity, no air gap has been assumed between beam splitter and sample surface).
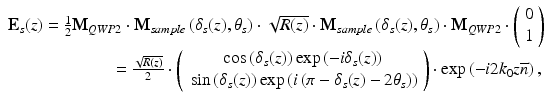
(34.4)
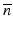is the mean refractive index of ordinary and extraordinary beam, and δ s (z) = Δn · z · k 0 (Δn is the refractive index difference between ordinary and extraordinary beam; for simplicity, no air gap has been assumed between beam splitter and sample surface).After recombination at the beam splitter BS, reference and sample beams interfere. The recombined beams travel towards the polarization-sensitive detection unit where they are split by polarizing beam splitter PBS into horizontal and vertical polarization components. The interference terms A H,V at the detectors, corresponding to the horizontal and vertical polarization channels, respectively, are:
![$$ {A}_{H,\kern-0.15em V}\left(z,\Delta \kern0.1em z\right)={A}_{0;H,\kern-0.15em V}\left(z,\Delta z\right)\cdot \cos \left[{\Phi}_{H,\kern-0.15em V}\left(\Delta z\right)\right] $$](/wp-content/uploads/2017/03/A76297_2_En_35_Chapter_Equ5.gif)
with
![$$ {A}_{0;H}\left(z,\Delta \kern0.1em z\right)=\frac{\sqrt{R(z)}}{2\sqrt{2}}\cdot \cos \left[{\delta}_s(z)\right]\cdot \left|\gamma \left(\Delta z\right)\right| $$](/wp-content/uploads/2017/03/A76297_2_En_35_Chapter_Equ6.gif)
![$$ {A}_{0;V}\left(z,\Delta \kern0.1em z\right)=\frac{\sqrt{R(z)}}{2\sqrt{2}}\cdot \sin \left[{\delta}_s(z)\right]\cdot \left|\gamma \left(\Delta z\right)\right| $$](/wp-content/uploads/2017/03/A76297_2_En_35_Chapter_Equ7.gif)
and
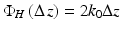
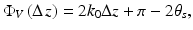
where A 0;H,V describe the envelopes of the interferometric signals caused by a single reflective site in the sample, Φ H,V are the corresponding phase functions of the interferometric fringes,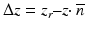 
is the optical path length difference between reference and sample arms, and |γ(Δz)| is the modulus of the complex degree of coherence of the interfering beams which describes the width of the interferometric signal (the axial point spread function). In Eqs. 34.7a and 34.7b an unimportant common phase term has been omitted.
(34.5)
(34.6a)
(34.6b)
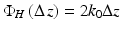
(34.7a)
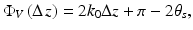
(34.7b)
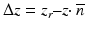is the optical path length difference between reference and sample arms, and |γ(Δz)| is the modulus of the complex degree of coherence of the interfering beams which describes the width of the interferometric signal (the axial point spread function). In Eqs. 34.7a and 34.7b an unimportant common phase term has been omitted.The terms cos(δ s (z)) and sin (δ s (z)) in Eqs. 34.6a and 34.6b oscillate slowly with depth z, if a sample with constant birefringence Δn is assumed, giving rise to intensity oscillations in the horizontal and vertical polarization channels which are π/2 out of phase. The cosine term in Eq. 34.5 oscillates rapidly with path difference Δz and describes the fringes of the interferometric signals, as typically observed in time domain OCT. The fringes of the horizontal and vertical components have a phase difference of π – 2θ s .
34.3.2.1 Quantification of Birefringence-Related Parameters
To calculate sample reflectivity R(z) and retardation δ s (z), we only need the envelopes of the interferometric signals A 0;H,V . For simplicity, we assume a coherence function of infinitesimal width (i.e., a nonzero amplitude only for Δz = 0) and can therefore omit the Δz dependence in the following equations:
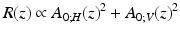
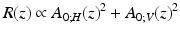
(34.8)
(34.9)
A closer look at the phase terms Φ H,V (Eqs. 34.7a and 34.7b) reveals that the information on the optic axis orientation θ s of the sample is encoded entirely in the phase difference ΔΦ = Φ H –Φ V of the two signals:
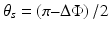
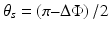
(34.10)
The unambiguous ranges of retardation and axis orientation, as provided by Eqs. 34.9 and 34.10, are 90° and 180°, respectively.
In time domain PS-OCT, amplitude and phase information can be retrieved, e.g., by lock-in demodulation [29] or by analytic continuation of the fully recorded fringe signals by a Hilbert transform [41]. In spectral domain PS-OCT, the inverse Fourier transform of the real-valued spectral interference signals directly yields complex valued signals of the form:
![$$ F{T}^{-1}\left\{{I}_{H,V}(k)\right\}\to {A}_{0;H,V}(z) \exp \left[i{\Phi}_{H,V}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_35_Chapter_Equ13.gif)
with I H,V (k) being the intensity as a function of wave number k in the horizontal and vertical polarization channel, respectively. For simplicity, the DC, autocorrelation, and mirror terms were omitted in Eq. 34.11. From these signals, amplitude and phase values can be directly taken and inserted into the corresponding parameters of Eqs. 34.8, 34.9, and 34.10 (it should be mentioned that the absolute phase values Φ H,V in Eq. 34.11 have no physical relevance; however, their difference provides the sample axis orientation via. Eq. 34.10).
(34.11)
As an example for imaging a birefringent structure in the human eye, Fig. 34.2 shows a circumpapillary scan recorded with a SD PS-OCT system in a healthy volunteer [45]. In this area, the RNFL forms rather thick bundles in the quadrants superior and inferior to the optic nerve head which are birefringent. Figure 34.2a shows a generic fundus photo illustrating the measured area: the scan was recorded approximately along the circular white line. Figure 34.2b shows the cross-sectional reflectivity (intensity) image. The increased thickness of the superior and inferior RNFL bundles is clearly visible. Figure 34.2c shows the retardation image, where the increased retardation caused by these nerve fiber bundles is clearly observed (color change from blue to green). Figure 34.3d shows the axis orientation image, where the two full color oscillations from left to right indicate the radial orientation of the nerve fibers (360° rotation of axis orientation).
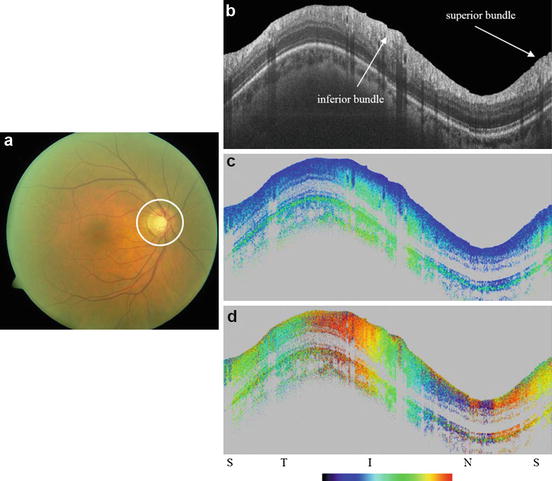
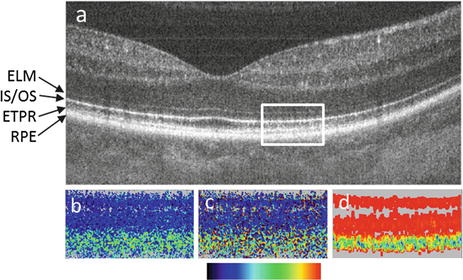
Fig. 34.2
Circumpapillary PS-OCT scan from healthy human retina. (a) Generic fundus photo illustrating scan geometry; the white circle indicates the approximate position of the scan line. (b–d): Circumpapillary B-scans. Scan diameter: ∼10° (corresponds to a circumference of ∼9.4 mm, equal to horizontal image width; optical image depth: 1.8 mm). (b) reflectivity (log scale); (c) retardation (color bar: 0–90°); (d) optic axis orientation (color bar: 0–180°). Orientation of scan from left to right: (S)uperior, (T)emporal, (I)nferior, (N)asal, (S)uperior (Reproduced from Götzinger et al. [45] by permission of the Optical Society of America)
Fig. 34.3
PS-OCT B-scan of a healthy human fovea. (a) Reflectivity (log scale), the white rectangle shows approximate areas of the zoom-ins (b)–(d); b retardation (color bar: 0–90°); (c) optic axis orientation (color bar: 0–180°); (d) DOPU (color bar: 0–1). ELM external limiting membrane, IS/OS boundary between inner and outer photoreceptor segments, ETPR end tips of photoreceptors, RPE retinal pigment epithelium (Reproduced from Götzinger et al. [45] by permission of the Optical Society of America)
34.3.2.2 Quantification of Depolarization
Since OCT is based on a coherent detection method, the degree of polarization (DOP) known from classical polarization optics cannot be directly measured. The light corresponding to a single speckle is always fully polarized, i.e., its DOP = 1 [37]. However, PS-OCT can obtain information on depolarization by analyzing the local distribution of polarization states among neighboring speckles. In case of a depolarizing tissue, polarization states of adjacent speckles will be uncorrelated, i.e., the polarization states vary randomly, while in other tissues (polarization maintaining or birefringent), the relation will be well defined. Therefore, depolarization is manifested by a scrambling of polarization states in PS-OCT images. To quantify this effect, we introduced a new parameter, the degree of polarization uniformity (DOPU), that has a strong formal relationship to DOP [28]. To quantify DOPU, we first calculate the Stokes vector S for each pixel in the PS-OCT image:
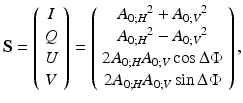
where I, Q, U, V denote the four Stokes vector elements. Then we average Stokes vectors over adjacent pixels by calculating the mean value of each Stokes vector element within a rectangular evaluation window (kernel) and derive DOPU:
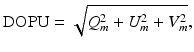
where the indices m indicate mean Stokes vector elements. DOPU can be regarded as a spatially averaged DOP and is closely related to the apparent degree of polarization obtained by temporal averaging [37] and to the quantity 
that was used to describe the local correlation of polarization states for detection of multiple scattered light by OCT [46].
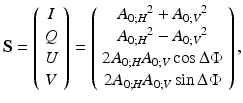
(34.12)
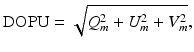
(34.13)
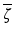that was used to describe the local correlation of polarization states for detection of multiple scattered light by OCT [46].In case of a polarization preserving or birefringent tissue, the value of DOPU should be close to 1; in case of a depolarizing layer, DOPU is lower than 1. In a typical application, the use of DOPU to segment the depolarizing RPE in PS-OCT images of the retina, a threshold value of DOPUthr = 0.7 – 0.8 is used. All image areas where DOPU < DOPUthr are classified as depolarizing.
Figure 34.3 shows an example of imaging a depolarizing structure in the human retina, obtained by a high-resolution SD PS-OCT system [45]. Figure 34.3a shows a cross-sectional reflectivity image (B-scan) through the fovea of a healthy human eye. In the posterior retina, four boundaries are marked: the external limiting membrane (ELM), the boundary between inner and outer photoreceptor segments (IS/OS), the end tips of the photo receptors (ETPR), and the RPE. Figure 34.3b, c show a zoom-in of retardation and axis orientation data into the posterior three of these layers. While the top two boundaries show rather constant color values (indicative of low retardation and constant axis orientation in this area of the retina), the bottom layer shows a striking difference: the color values are scrambled, i.e., more or less random. The DOPU image (Fig. 34.3d) demonstrates this difference even better: while the IS/OS and the ETPR show DOPU values close to 1 (red color), the RPE is strongly depolarizing (green to blue colors, DOPU < 0.7).
34.3.3 Spectral Domain and Fiber-Optic Implementations
Several variants of the basic setup described in Sect. 34.3.1 have been reported. While the initial work was based on time domain technology in various forms [13, 14, 29, 41], spectral domain variants gained more attraction after the discovery of their huge sensitivity advantage. Bulk optic [21, 47] and fiber-optic [45] setups were reported, employing either a two-channel spectrometer with a single line scan camera [21] or two separate spectrometers, each equipped with its own camera [47]. Spectrometer-based SD PS-OCT systems require either a nearly perfect pixel-to-pixel correspondence of the spectrometers recording the two channels (otherwise, depth-dependent artifacts of mainly the axis orientation can occur [47]) or an additional post-processing step that corrects for the spectral mismatch (this is mandatory for single camera systems [21]). These spectrometer type systems typically operate in the 840 nm wavelength regime.
A related variant is based on swept source (SS) technology which is preferred at the longer wavelength centered around 1,050 nm. This technique has the advantage of improved imaging depth beyond the RPE, down to the choroid and sclera [48–51], however, is presently more expensive. Different versions of PS-OCT at this wavelength have been reported for retinal imaging, employing single [52] and multiple [53] input polarization states.
Bulk optic PS-OCT setups have the advantage that the optical components used are very stable with respect to their polarization properties. Once aligned, they can be used without recalibration over extended periods of time. However, for commercial instruments, fiber-optic systems are preferred since they can be quite robust and need little optical alignment. The use of normal single-mode (SM) fibers (that are commonly used for intensity-based OCT), however, causes a problem for PS-OCT: the fiber is birefringent, and the exact amount of birefringence varies with environmental influences like bending and temperature. Therefore, it is neither easily possible to achieve a constant polarization state (e.g., circular) at the sample nor to maintain the polarization state of the light beam passing the fiber. Therefore, SM fiber-based PS-OCT systems usually require to probe the sample with more than one polarization state and retrieve the sample’s polarizing properties by differential measurements and elaborate algorithms that compensate for possible changes of the light’s polarization state within the fiber [54].
A solution to this problem is the use of polarization-maintaining (PM) fibers [45, 55, 56]. PM fiber-based PS-OCT systems can employ the same principles as described in Sect. 34.3.2. The amplitudes of the two orthogonal light components are well preserved throughout the PM fibers, enabling a direct calculation of sample reflectivity and retardation. However, due to the different propagation velocities of the two orthogonal modes in the PM fiber, the phase relation between the modes is lost, destroying the original elliptic polarization state backscattered from the sample. The phase difference, however, is needed to calculate axis orientation and Stokes vector. To solve this problem, the lengths of the PM fibers in the sample and reference arms have to be carefully matched. In this case, the phase differences in the two arms cancel each other. A remaining phase difference caused, e.g., by imperfect fiber length matching can be compensated in a post-processing step [45]. This method provides correct relative axis orientations; to obtain the absolute axis orientation, a calibration measurement is needed.
As an example of a state-of-the-art PS-OCT retinal scanner, Fig. 34.4 shows a sketch of one of our newest instruments. More than 200 patients with various diseases have been imaged with this device and several of the images presented in this chapter were recorded with the system. It is a PM fiber-based SD PS-OCT instrument employing a two-channel spectrometer with a single camera. An SLD emits a light beam centered at ∼840 nm whose polarization state is matched by a polarization controller (paddle) PC to the orientation transmitted by the PM fiber polarizer. A 90:10 splitter directs 10 % of the beam to the sample and 90 % to the reference mirror. After passing the QWP, the sample light is in a circular polarization state and raster scanned via the galvanometer scanner and a telescope (lenses L1 and L2) over the retina. In the reference arm, a QWP ensures equal reference power in both polarization states, as described above. After recombination at the 90:10 splitter (90 % of the sample beam power is transmitted into the detection arm), the beams interfere and are guided to the polarizing beam splitter which separates the horizontal and the vertical state. The two polarization states are spectrally dispersed by a diffraction grating and imaged adjacent to each other onto a high-speed CMOS line scan camera (Basler sprint, 4,096 pixels).
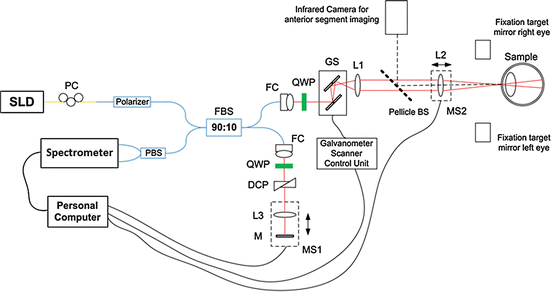
Fig. 34.4
Sketch of wide-field SD PS-OCT system. SLD super luminescent diode, PC polarization controller, FBS fiber non-polarizing beam splitter, PBS fiber polarizing beam splitter, FC fiber collimator, QWP quarter wave plate, DCP dispersion-compensating prisms, L lens, MS motorized stage, GS galvanometer scanner, M mirror, Pellicle BS pellicle beam splitter; yellow lines, single-mode fibers; red lines, free space beam paths; blue lines, polarization-maintaining fiber; black lines, cable connection (Reproduced from Zotter et al. [57] by permission of the Optical Society of America)
The camera is operated at a line rate of 70 kHz. With a light power of 730 μW at the cornea, a maximum sensitivity of 98 dB is obtained, with a roll-off of 8 dB over an imaging depth of 1.8 mm. The axial resolution is 7.8 μm in air or ∼5.7 μm in tissue (assuming a group index of ∼1.38). The maximum scan field size of the instrument is 40° × 40°. Various scan patterns, ranging from 512(x) × 125(y) up to 1,024 × 250 A-scans, are available. More details on the instrument can be found in ref. [57].
The processing of data acquired with this system comprises the following steps: the two adjacent spectra provided by the camera are separated and numerically resampled to achieve a pixel-to-pixel correspondence (this step is equivalent to squeezing/compressing one spectrum until it fits the width of the other one). Afterwards, standard post-processing steps (subtraction of the mean spectrum, rescaling from wavelength to wavenumber space, inverse Fourier transform) are performed. Then, amplitude and phase difference data are calculated, from which retardation, axis orientation, Stokes vectors, and DOPU values are obtained as described in detail above. Since the birefringence-related data of retinal structures are obtained by a measurement through the birefringent cornea, the influence of the cornea has to be compensated for. This is performed by retrieving the polarization state at the retinal surface (which corresponds to the influence exerted by the cornea) and subsequently compensating the polarization state distortions caused by the cornea by a software-based algorithm [58].
34.4 Applications of PS-OCT to Retinal Imaging
34.4.1 Imaging of the Macular Region
The macula represents the most precious location on the retina because it contains the fovea, which represents, in the healthy eye, the spot with the best vision. A variety of different diseases (e.g., age-related macula degeneration (AMD) and diabetic retinopathy (DR)) may alter the normal structure in the macular region, and in recent years, OCT has become an indispensable clinical tool for an accurate determination of these changes.
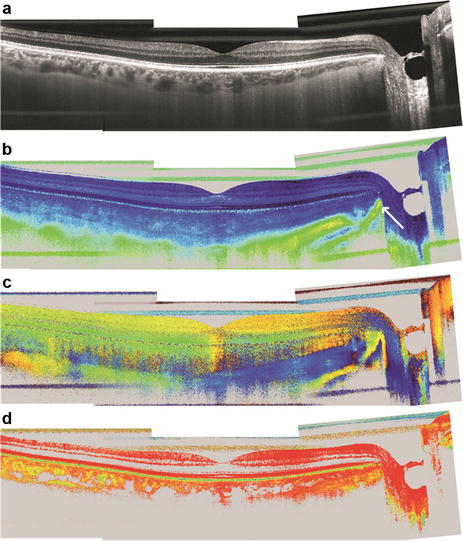
PS-OCT provides additional contrast that is not accessible with standard OCT. Figure 34.5 shows imaging examples obtained in a healthy volunteer recorded at 840 nm with a large field of view scan [57]. Within the DOPU images (e, j), the RPE can be easily outlined because it contains particles (e.g., pigments) that scramble the polarization state of the backscattered light. Birefringence introduced by Henle’s fiber layer causes an increased retardation in the macula area (c.f. increased retardation at the junction between inner and outer segments of photoreceptors (IS/OS) and end tips of photoreceptors (ETPR) indicated by arrows in Fig. 34.5c, h). Note that because of the orientation of the fibers in Henle’s fiber layer, no increase in retardation can be observed in the fovea centralis (c.f. dark blue color at the IS/OS junction). The instrument operates at an imaging speed of 70 kHz. This high speed enables, in order to reduce speckle noise and enhance the signal to noise ratio, recording and averaging of several B-scans at the same location resulting in high-quality scans shown in Fig. 34.5g–j.
Fig. 34.5
PS-OCT measurement results recorded from a healthy human volunteer (scan angle: 40 × 40°, 1,024 × 250 A-scans). (a) Depth integrated OCT en face view, yellow line indicates the location of the corresponding B-scans. (b) Intensity B-scan on logarithmic gray scale. Yellow rectangle indicates magnified area that is shown in b1. (c) Retardation image (color scale 0–90°). The arrows indicate increased retardation at the IS/OS junction caused by Henle’s fiber layer. (d) Optic axis orientation (color scale 0–180°). (e) DOPU image (color scale 0–1). Yellow rectangle indicates magnified area shown in e1. (f) Segmented depolarizing material (red) overlaid with the intensity image. Yellow rectangle indicates magnified area shown in f1. (g) Average of 50 intensity B-scans recorded at the same position. (h) Average retardation image. (i) Average optic axis orientation image. (j) DOPU image calculated from a temporal window over 50 B-scans. (k) Depth summation of the number of depolarizing pixels along each A-scan within the 3-D data set (color scale 0–100 μm). Areas with low signal quality are displayed in white (Reproduced from Zotter et al. [57] by permission of the Optical Society of America)
In order to illustrate the similarities between different wavelength regions, Fig. 34.6 shows averaged PS-OCT images recorded at 1,040 nm with a swept source system [52]. Essentially the same polarization characteristics as with the 840 nm system can be observed within the anterior layers, the photoreceptor layers, and the RPE. However, the longer wavelength region provides a better penetration into choroid and sclera. The sclera is known to be highly birefringent which can directly be observed in Fig. 34.6b by the strong increase of retardation within this layer. This specific characteristic of the sclera can be used in order to segment the posterior boundary of the choroid based on PS-OCT data [59, 60].
