(3.1)
where k is the wave number, R is a point in space, and n(R) is the index of refraction. Considering a random medium, n(R) acts as a stochastic variable for different realizations of tissue with given macroscopic optical parameters. Equation 3.1 cannot be solved exactly in closed form. Some early attempts to solve Eq. 3.1 were based on the geometric optics approximation [36], which ignores diffraction effects, and on perturbation theories widely known as the Born approximation and Rytov approximation [37]. An alternative method was developed, independent of each other, by Lutomirski and Yura [38] and by Feizulin and Kravtsov [39]. This technique is called the extended Huygens–Fresnel (EHF) principle. It extends the Huygens–Fresnel principle to deal with media that exhibit a random spatial variation in the index of refraction. This principle follows directly from Green’s theorem [40] and the Kirchhoff approximation [40] applied to the scalar wave equation together with the use of a field reciprocity theorem. Yura and Hanson [41, 42] have applied the EHF principle to paraxial wave propagation through an arbitrary ABCD system in the presence of random inhomogeneities. An arbitrary ABCD system refers to an optical system that can be described by the so-called ABCD ray-transfer matrix [43]. For the present cases of interest, the ABCD ray-transfer matrix is real, and the field in the output plane is then given by [41]
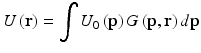
(3.2)
![$$ G\left(\mathbf{p},\mathbf{r}\right)={G}_0\left(\mathbf{p},\mathbf{r}\right) \exp \left[i\varphi \left(\mathbf{p},\mathbf{r}\right)\right], $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ3.gif)
(3.3)
![$$ {G}_0\left(\mathbf{p},\mathbf{r}\right)=-\frac{ik}{2\pi B} \exp \left[-\frac{ik}{2B}\left(A{p}^2-2\mathbf{p}\cdot \mathbf{r}+D{r}^2\right)\right], $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ4.gif)
(3.4)
3.2.2 Calculating the OCT Signal: Time Domain
A time-domain OCT system [1] is based on a broad bandwidth light source (SLD), a Michelson interferometer with a movable reference mirror, and a photodetector. The rotationally symmetric sample arm geometry of such an OCT system is depicted in Fig. 3.1, where a lens with focal length f is placed at a distance d from the tissue surface. The optical path length of the reference arm in the Michelson interferometer is matched to the optical depth of the focal plane, whereby the configuration – due to backscattering – is probing the layer of the tissue coinciding with the focal region.
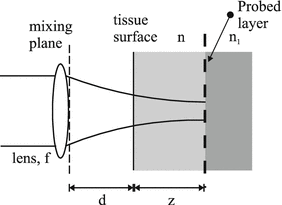

Fig. 3.1
Sample arm geometry of the OCT system
For the wavelengths of interest in the NIR region and, e.g., in the case of human skin, light scattering in the bulk tissue is predominantly taking place in the forward direction [44]. Hence, the scattering phase function σ(θ,z) can be modeled as a sum of a small-angle scattering phase function σ 1(θ,z) that tends to zero for θ > π/2 and a constant but relative small isotropic term included to incorporate a backscattered contribution [8, 13]:
![$$ \sigma \left(\theta, z\right)=\left[1-2{p}_b(z)\right]{\sigma}_1\left(\theta, z\right)+2{p}_b(z), $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ5.gif)
where p b (z) denotes the backscattering coefficient as a function of the depth. For tissues, the quantity p b will normally be much smaller than unity, i.e., p b <<1; see, for example, Ref. [13].
![$$ \sigma \left(\theta, z\right)=\left[1-2{p}_b(z)\right]{\sigma}_1\left(\theta, z\right)+2{p}_b(z), $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ5.gif)
(3.5)
It was noted above that the EHF principle is based on the paraxial approximation and therefore valid for small-angle forward scattering. In particular, it can be shown that the paraxial approximation is valid up to 30°, i.e., 0.5 rad [43]. Because most tissues are characterized by rms scattering angles below this limit, the EHF principle may be used to describe light propagation in tissue retaining both amplitude and phase information. Also, the bulk tissue absorption is neglected in the present calculation, because in the case of most tissues, the scattering essentially accounts for the signal attenuation [44]. Basically including the absorption would result in an overall exponential decay. Thus, bulk homogeneous tissue is characterized by a scattering coefficient μ s, a root-mean-square scattering angle θ rms or asymmetry parameter g [45], and a mean index of refraction n. Furthermore, the bulk tissue is modeled as a material with scatterers randomly distributed over the volume of interest.
Consider an optical field that is narrowband and non-monochromatic, i.e., the spectral width of the light source Δν is much smaller than the center frequency ν. Light sources characterized as “broad band” in relation to OCT also fulfills this condition. At a spatial coordinate p and time t, such an optical field may be expressed in terms of a (temporally) slowly varying complex amplitude A(t) where the characteristic temporal scale of the complex envelope amplitude A is much less than 1/ν0. In addition it is assumed that the reference field, U R , and the incident sample field, U Si , are of Gaussian shapes:
![$$ {U}_R\left(\mathbf{p},t\right)=\sqrt{\frac{P_R}{\pi {w}_0^2} \exp \left[-\frac{{\left|\mathbf{p}\right|}^2}{2}\left(\frac{1}{w_0^2}+\frac{ik}{f}\right)\right]}A(t) \exp \left[i{\omega}_Rt+{\varphi}_R(t)\right], $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ6.gif)
![$$ {U}_{Si}\left(\mathbf{p},t\right)=\sqrt{\frac{P_s}{\pi {w}_0^2} \exp \left[-\frac{{\left|\mathbf{p}\right|}^2}{2}\left(\frac{1}{w_0^2}+\frac{ik}{f}\right)\right]}A(t) \exp \left[i{\omega}_st+{\varphi}_s(t)\right], $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ7.gif)
where P R and P S are the powers of the reference and input sample beams, respectively; w 0 is the 1/e intensity radius of these beams in the lens plane, k = 2π /λ; λ is the center wavelength of the source in vacuum; ω R and ω S are the angular frequencies of the reference and input sample beams, respectively; and φ R and φ S are the phases of the reference field and input sample field, respectively.
![$$ {U}_R\left(\mathbf{p},t\right)=\sqrt{\frac{P_R}{\pi {w}_0^2} \exp \left[-\frac{{\left|\mathbf{p}\right|}^2}{2}\left(\frac{1}{w_0^2}+\frac{ik}{f}\right)\right]}A(t) \exp \left[i{\omega}_Rt+{\varphi}_R(t)\right], $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ6.gif)
(3.6)
![$$ {U}_{Si}\left(\mathbf{p},t\right)=\sqrt{\frac{P_s}{\pi {w}_0^2} \exp \left[-\frac{{\left|\mathbf{p}\right|}^2}{2}\left(\frac{1}{w_0^2}+\frac{ik}{f}\right)\right]}A(t) \exp \left[i{\omega}_st+{\varphi}_s(t)\right], $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ7.gif)
(3.7)
The mixing of the backscattered or reflected sample field U S from the probed layer with the reference field U R on the photodetector of the OCT system gives rise to a heterodyne signal current i(z) [9]:
![$$ i(z)\propto \left|\gamma \left(\tau \right)\right|\mathrm{R}\mathrm{e}\left[{\displaystyle \int {U}_R\left(\mathbf{p}\right)\kern0.1em }{U}_S^{*}\left(\mathbf{p}\right)d\mathbf{p}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ8.gif)
where the integration is taken over the area of the photodetector. Re[·] denotes the real part, and τ denotes the time difference between the propagation times of the reference and sample beams. ∣γ(τ)∣ is the modulus of the normalized temporal coherence function of the source.
![$$ i(z)\propto \left|\gamma \left(\tau \right)\right|\mathrm{R}\mathrm{e}\left[{\displaystyle \int {U}_R\left(\mathbf{p}\right)\kern0.1em }{U}_S^{*}\left(\mathbf{p}\right)d\mathbf{p}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ8.gif)
(3.8)
Because a random medium is considered, the mean square heterodyne signal current 〈i 2(z)〉 should be calculated, which is proportional to the heterodyne signal power. It can be shown to be given by [9, 18]:
![$$ \left\langle {i}^2(z)\right\rangle =2{\alpha}^2{\left|\gamma \left(\tau \right)\right|}^2\mathrm{R}\mathrm{e}\left[{\displaystyle \iint {\Gamma}_S\left({\mathbf{p}}_1,{\mathbf{p}}_2;z\right){\Gamma}_R\left({\mathbf{p}}_1,{\mathbf{p}}_2\right)}d{\mathbf{p}}_1d{\mathbf{p}}_2\right], $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ9.gif)
where
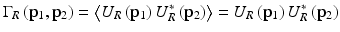
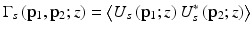
are the mutual coherence functions of the reference and the reflected sample optical fields in the mixing plane. The angular brackets denote an ensemble average over the statistical properties of the tissue. Physically, the heterodyne mixing process takes place on the photosensitive surface of the detector in the focal plane of the “mixing” lens. However, Fried [46] has shown mathematically that one can identically compute the mean square heterodyne photocurrent in a plane directly in front of the mixing lens at the side facing the sample, and, accordingly, p 1, p 2 are two-dimensional vectors in this plane transverse to the optical axis. The quantity α is a conversion factor for power to current and equals (q e η/hν), where q e is the electronic charge, η the detector quantum efficiency, ν the optical center frequency, and h Planck’s constant. In the present analysis, without loss of generality, the temporal coherence function is approximated with a rectangular function of width τ c, the coherence time of the source.
![$$ \left\langle {i}^2(z)\right\rangle =2{\alpha}^2{\left|\gamma \left(\tau \right)\right|}^2\mathrm{R}\mathrm{e}\left[{\displaystyle \iint {\Gamma}_S\left({\mathbf{p}}_1,{\mathbf{p}}_2;z\right){\Gamma}_R\left({\mathbf{p}}_1,{\mathbf{p}}_2\right)}d{\mathbf{p}}_1d{\mathbf{p}}_2\right], $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ9.gif)
(3.9)
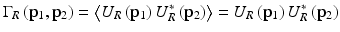
(3.10)
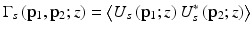
(3.11)
Details of the derivation of the mutual coherence function Γ S are given in Appendix under the assumption that the forward propagated light can be considered statistically independent from the backscattered light. To obtain a closed-form expression including the intermediate ranges of propagation, the single-scattering solution and the solution for large optical depths are interpolated, as outlined in Appendix, yielding the following squared signal contribution from within the coherence gate around the depth z:
![$$ {\left\langle {i}^2(z)\right\rangle}_{coh\_ gate}\approx \frac{2{\alpha}^2{P}_R{P}_S{\sigma}_b}{\pi^2}{{\displaystyle \int \left[\frac{e^{-{\mu}_sz} \exp \left\{-{r}^2/{w}_H^2\right\}}{w_H^2}+\frac{\left(1-{e}^{-{\mu}_sz}\right){e}^{-2{p}_b{\mu}_sz} \exp \left\{-{r}^2/{w}_S^2\right\}}{w_S^2}\right]}}^2d\mathbf{r}, $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ12.gif)
where the effective backscattering cross section of the layer being probed is defined as σ b = 4πp b μ s l c /k 2. Here l c denotes the coherence length of the source given by cτ c . In Eq. 3.12 it is assumed that μ s l c <<1.
![$$ {\left\langle {i}^2(z)\right\rangle}_{coh\_ gate}\approx \frac{2{\alpha}^2{P}_R{P}_S{\sigma}_b}{\pi^2}{{\displaystyle \int \left[\frac{e^{-{\mu}_sz} \exp \left\{-{r}^2/{w}_H^2\right\}}{w_H^2}+\frac{\left(1-{e}^{-{\mu}_sz}\right){e}^{-2{p}_b{\mu}_sz} \exp \left\{-{r}^2/{w}_S^2\right\}}{w_S^2}\right]}}^2d\mathbf{r}, $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ12.gif)
(3.12)
The quantities w H and w S are the 1/e irradiance radii in the target plane in the absence and presence of scattering, respectively, given by [12]
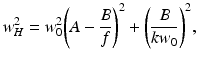
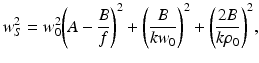
where ρ 0 denotes the lateral coherence length of the reflected sample field in the plane in which the mixing calculated [12]
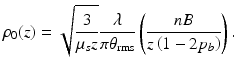
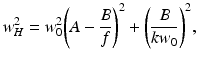
(3.13)
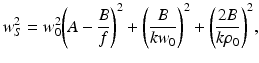
(3.14)
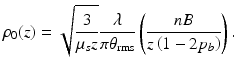
(3.15)
Here the root-mean scattering angle, θ rms, is related to the anisotropy parameter g:
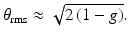
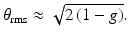
(3.16)
Performing the integration over the probed layer (see Fig. 3.1) in Eq. 3.12 and simplifying, the following expression for the mean square heterodyne signal current is obtained:
![$$ \begin{array}{l}{\left\langle {i}^2(z)\right\rangle}_{coh\_ gate}\approx \frac{\alpha^2{P}_R{P}_s{\sigma}_b}{\pi {w}_{{}^{{}^H}}^2}\\ {}\kern2.28em \times \left[{e}^{-2{\mu}_sz}+\frac{4{e}^{-{\mu}_sz}{e}^{-2{p}_b{\mu}_sz}\left(1-{e}^{-{\mu}_sz}\right)}{1+\frac{w_S^2}{w_H^2}}+{\left(1-{e}^{-{\mu}_sz}\right)}^2{e}^{-4{p}_b{\mu}_sz}\frac{w_H^2}{w_S^2}\right]\\ {}\kern1.8em ={\left\langle {i}^2\right\rangle}_0\Psi (z).\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ17.gif)
![$$ \begin{array}{l}{\left\langle {i}^2(z)\right\rangle}_{coh\_ gate}\approx \frac{\alpha^2{P}_R{P}_s{\sigma}_b}{\pi {w}_{{}^{{}^H}}^2}\\ {}\kern2.28em \times \left[{e}^{-2{\mu}_sz}+\frac{4{e}^{-{\mu}_sz}{e}^{-2{p}_b{\mu}_sz}\left(1-{e}^{-{\mu}_sz}\right)}{1+\frac{w_S^2}{w_H^2}}+{\left(1-{e}^{-{\mu}_sz}\right)}^2{e}^{-4{p}_b{\mu}_sz}\frac{w_H^2}{w_S^2}\right]\\ {}\kern1.8em ={\left\langle {i}^2\right\rangle}_0\Psi (z).\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ17.gif)
(3.17)
The quantity 〈i 2〉0 = α 2 P R P S σ b /π(w H )2 is the mean square heterodyne signal current in the absence of scattering, and the terms contained in the brackets are the heterodyne efficiency factor Ψ(z). The quantity Ψ(z) is the reduction in the heterodyne signal-to-noise ratio due to the scattering of the tissue. The first term in the brackets of Eq. 3.17 represents the contribution due to single scattering. The third term is the multiple-scattering term, and the second term is the cross term. Physically, the cross term is the coherent mixing of the unscattered and the multiple-scattered light. A comparison between the analytical approximation of Ψ(z), given in Eq. 3.17, and the exact numerical calculation is given in Ref. [47] showing reasonable agreement. The validity of the above expression has been explored by comparing the model with advanced Monte Carlo studies and confirms that the analytical result provides a feasible model for investigating the qualitative behavior of the OCT configuration; see Sect. 3.4.
3.2.2.1 Dynamic Focusing: Diffuse Reflectance
If one applies dynamic focusing, the focal plane will ideally be arranged to move in accordance with the position of the coherence gate. This situation can be analyzed by setting fA = B and A = 1 in Eqs. 3.13 and 3.14:
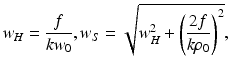

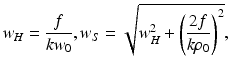
(3.19)

(3.20)
For lateral separations much less (greater) than the coherence length, ρ 0(z), the field can be considered to be mutually coherent (incoherent). Because of the diffuse backscattering from the layer being probed, ρ 0(z) is determined only by the propagation back through the tissue from this layer to the mixing plane. As a consequence, ρ 0(z) is the lateral coherence length in the mixing plane of a point source located in the tissue plane being probed. For the geometry of interest, it can be shown [47] that
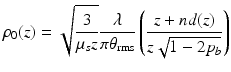
where d(z) = f − z/n, and θ rms ≈ [2(1 − g)]1/2. The second term in the brackets of Eq. 3.21 indicates that the lateral coherence length increases with increasing distance between the tissue surface and the mixing plane.
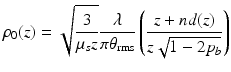
(3.21)
The dependence of the lateral coherence length on the position of the scattering medium relative to the observation plane is the so-called shower-curtain effect [18, 32]. In general, the shower-curtain effect implies that the lateral coherence length obtained for the case when the scattering medium is close to the radiation source is larger than for the case when the scattering medium is close to the observation plane. Physically, this is due to the fact that a distorted spherical wave approaches a plane wave as it further propagates through a non-scattering medium. As a consequence, e.g., from a distance, one can see a person immediately behind a shower curtain, but the person cannot see you. The effect is well known for light propagation through the atmosphere as discussed by Dror et al. [32], but has been omitted in previous theoretical OCT models [9]. However, due to the finite distance between the focusing lens and the tissue, the effect is inevitably present in practical OCT systems. Finally, the reflection characteristics of the tissue play a vital role for the shower-curtain effect.
It is only in the very superficial layers of highly scattering tissue that it is possible to achieve diffraction-limited focusing. In this region, the spot size is given by 2w H . At deeper probing depths, the spot size is dependent on the scattering properties and given by 2w S . It is seen from Eqs. 3.20 and 3.21 that the spot size is degraded due to multiple scattering when the probing depth is increased. This is illustrated in Fig. 3.2, where the intensity pattern is shown as a function of the probing depth z in the tissue using Eq. 3.72, thus illustrating spot size degradation in, e.g., microscopy.
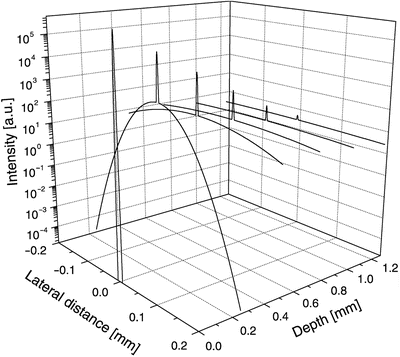

Fig. 3.2
The intensity pattern as a function of the probing depth z in the tissue (λ = 814 nm, μ s = 10 mm−1, g = 0.955 (θ rms = 0.3 rad), n = 1.4, f = 5 mm, w 0 = 0.5 mm)
From Eq. 3.18 an expression for the OCT signal for large optical depths can be obtained as
![$$ \left\langle {i}^2(z)\right\rangle \propto \frac{ \exp \left(-4{p}_b{\mu}_sz\right)}{\mu_s\left(1-g\right){z}^3},{\mu}_sz>>1. $$
” src=”/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ22.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(3.22)</DIV></DIV></DIV><br />
<DIV class=Para>From this expression it is observed that the denominator is proportional to the reduced scattering coefficient <SPAN class=EmphasisTypeItalic>μ</SPAN> <SUB><SPAN class=EmphasisTypeItalic>s</SPAN> </SUB>(1-<SPAN class=EmphasisTypeItalic>g</SPAN>), while the numerator will be close to 1 for small values of <SPAN class=EmphasisTypeItalic>p</SPAN> <SUB><SPAN class=EmphasisTypeItalic>b</SPAN> </SUB>. Consequently, if the signal for large optical depths is observed, it cannot be expected to derive both <SPAN class=EmphasisTypeItalic>μ</SPAN> <SUB><SPAN class=EmphasisTypeItalic>s</SPAN> </SUB>and <SPAN class=EmphasisTypeItalic>g</SPAN> from the measured depth profiles.</DIV></DIV><br />
<DIV id=Sec8 class=]()




3.2.2.2 Dynamic Focusing: Specular Reflectance
If, instead of diffuse backscattering, one had a specular reflection at the layer being probed, the corresponding mutual coherence function for plane waves would apply. Using this mutual coherence function and p b <<1, the following expression is obtained for the heterodyne efficiency factor:
![$$ \Psi (z)=\left[{e}^{-2{\mu}_sz}+\left(1-{e}^{-2{\mu}_sz}\right)\frac{w_H^2}{w_s^2}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ23.gif)
and
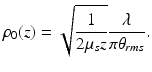
![$$ \Psi (z)=\left[{e}^{-2{\mu}_sz}+\left(1-{e}^{-2{\mu}_sz}\right)\frac{w_H^2}{w_s^2}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ23.gif)
(3.23)
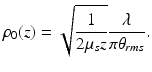
(3.24)
It is obvious from Eq. 3.24 that the shower-curtain effect would not be present in the case of specular reflection at the tissue discontinuity, in contrast to the case of diffuse backscattering. However, it is important to note that it is diffuse backscattering which actually occurs in the case of tissue.
3.2.2.3 Collimated Sample Beam
In the case of a collimated sample beam, the expressions for w H and w S in Eqs. 3.13 and 3.14 need to be rewritten:
![$$ {w}_H^2=\underset{f\to \infty }{ \lim}\left[{w}_0^2{\left(1-\frac{d+z/n}{f}\right)}^2+{\left(\frac{d+z/n}{k{w}_0}\right)}^2\right]={w}_0^2+{\left(\frac{d+z/n}{k{w}_0}\right)}^2 $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ25.gif)
![$$ {w}_S^2=\underset{f\to \infty }{ \lim}\left[{w}_H^2+{\left(\frac{2\left(d+z/n\right)}{k{\rho}_0}\right)}^2\right]={w}_0^2+{\left(\frac{d+z/n}{k{w}_0}\right)}^2+{\left(\frac{2\left(d+z/n\right)}{k{\rho}_0}\right)}^2, $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ26.gif)
where it has been used that A = 1 and B = d + z/n. In order to find the heterodyne efficiency factor, these expressions must be inserted in Eq. 3.17, and moreover, the expression for ρ 0 should be chosen in accordance with the reflection characteristics of the probed layer.
![$$ {w}_H^2=\underset{f\to \infty }{ \lim}\left[{w}_0^2{\left(1-\frac{d+z/n}{f}\right)}^2+{\left(\frac{d+z/n}{k{w}_0}\right)}^2\right]={w}_0^2+{\left(\frac{d+z/n}{k{w}_0}\right)}^2 $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ25.gif)
(3.25)
![$$ {w}_S^2=\underset{f\to \infty }{ \lim}\left[{w}_H^2+{\left(\frac{2\left(d+z/n\right)}{k{\rho}_0}\right)}^2\right]={w}_0^2+{\left(\frac{d+z/n}{k{w}_0}\right)}^2+{\left(\frac{2\left(d+z/n\right)}{k{\rho}_0}\right)}^2, $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ26.gif)
(3.26)
3.2.2.4 Numerical Results
In Fig. 3.3, the calculated heterodyne efficiency factor Ψ(z) from Eq. 3.18 is shown as a function of depth z of the tissue sample for typical parameters of human skin tissue. The curves are shown for the cases of diffuse backscattering with (dashed) and without (dash-dot) the shower-curtain effect included and for the specular reflection (solid), respectively. In addition, the case of pure single scattering (dotted) is included for comparison. At shallow depths single backscattering dominates. Due to multiple scattering, the slope is changed and Ψ(z) becomes almost constant for three cases (curves 1−3). The important difference is, however, that the change of slope occurs at different depths. This is due to the shower-curtain effect leading to an appreciable enhancement of Ψ(z) and with it the heterodyne signal, which is obtained by comparing curves 1 and 2 in Fig. 3.3. Physically, this increase in the heterodyne signal is due to an enhanced spatial coherence of the multiple-scattered light.
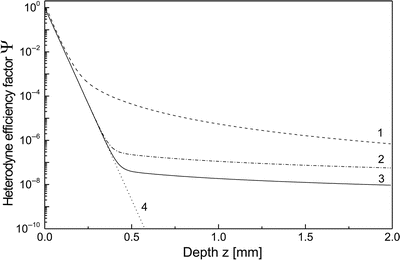

Fig. 3.3
Ψ(z) as a function of z for diffuse backscattering with the shower-curtain effect included (curve 1) and for specular reflection (curve 3). Curve 2 is calculated for diffuse backscattering without the shower-curtain effect, and curve 4 is the case of pure single backscattering; λ = 814 nm, μ s = 20 mm−1, g = 0.955 (θ rms = 0.3 rad), n = 1.4, f = 5 mm, w 0 = 0.5 mm (From Ref. [12])
In Fig. 3.4, Ψ(z) from Eq. 3.18 is shown as a function of depth z for μ s = 10 mm−1 and three values of g within the range of validity of the EHF principle. The curves are computed for the case of diffuse backscattering. This figure demonstrates the degree of sensitivity of the heterodyne efficiency factor with respect to changes in the asymmetry parameter. Moreover, in Fig. 3.5, Ψ(z) from Eq. 3.18 is shown as a function of depth z for g = 0.95 and three values of μ s within the range of interest with respect to tissue [44]. The curves are again computed for the case of diffuse backscattering. This figure demonstrates the degree of sensitivity of the heterodyne efficiency factor with respect to changes in the scattering coefficient.
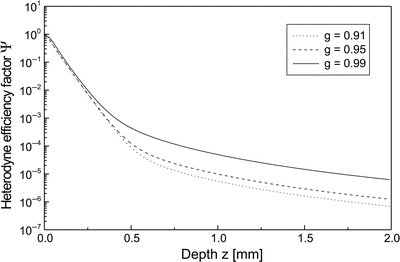
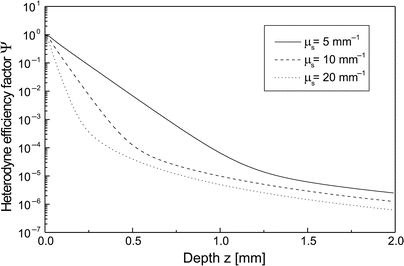

Fig. 3.4
Ψ(z) as a function of z for μ s = 10 mm−1 and three values of g. The curves are for the case of a diffuse backscattering at the discontinuity and inclusion of the shower-curtain effect (λ = 814 nm, n = 1.4, f = 5 mm, w 0 = 0.5 mm)

Fig. 3.5
Ψ(z) as a function of z for g = 0.95 and three values of μ s within a range of interest with respect to tissue. The curves are for the case of a diffuse backscattering at the discontinuity and inclusion of the shower-curtain effect (λ = 814 nm, n = 1.4, f = 5 mm, w 0 = 0.5 mm)
3.2.2.5 Choice of Scattering Function
In the present modeling of the OCT geometry, a Gaussian volume scattering function [20] for the forward scattered part is used; see Eqs. 3.5 and 3.64. The motivation for this choice of scattering function is the ability to obtain an accurate analytical engineering approximation, valid for all values of the optical depth. Using the Henyey–Greenstein scattering function [48], which is widely used in approximating the angular scattering dependence of single-scattering events in some biological media [44, 49], the corresponding analytical approximation is not as accurate as for the case of a Gaussian scattering function. However, a numerical computation using the exact expressions may be carried out instead. Hence, both scattering functions may be used in the modeling of the OCT geometry presented in this chapter.
3.2.2.6 Signal-to-Noise Ratio (SNR) and Estimation of the Maximum Probing Depth
Without loss of generality, an OCT system with shot-noise-limited operation is considered here for calculating the signal-to-noise ratio (SNR) with the purpose of estimating the maximum probing depth. The only significant source of noise is the shot noise caused by the reference beam. For a photoconductive detector, the mean square noise power N p can then be expressed as [50]

where R l is the resistance of the load, G ca the gain associated with the current amplifier, and B w the system bandwidth. The corresponding mean heterodyne signal power S(z) is given by [46]
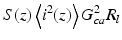
where 〈i 2(z)〉 is given by Eq. 3.17. Hence, the mean signal-to-noise ratio SNR(z) is given by
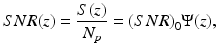
where the signal-to-noise ratio in the absence of scattering (SNR)0 is given by
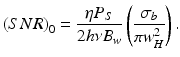

(3.27)
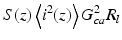
(3.28)
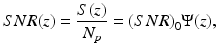
(3.29)
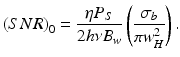
(3.30)
In the case of interest where the focal plane coincides with the probed layer, the following expression for (SNR)0 is obtained:
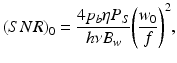
where it has been used that σ b = 4πp b μ s l c /k 2.
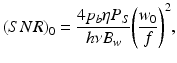
(3.31)
The maximum probing depth is of considerable interest in the characterization and optimization of an OCT system when used for imaging in highly scattering tissue. The maximum probing depth may be calculated by using the model presented above. Details of the calculation are found in Ref. [31], where the calculation of the maximum probing depth z max is based on the minimum acceptable SNR in the case of shot-noise-limited detection. In the calculations, a value of 3 is used as the minimum acceptable signal-to-noise ratio, i.e., SNR(z max ) = 3.
An important conclusion of Ref. [31] is that, in general, z max depends on the focal length at small values of the scattering coefficient, but is independent of the focal length at larger values of the scattering coefficient. A similar behavior is observed for z max as a function of μ s and the 1/e intensity radius of the sample beam being focused. This behavior is due to multiple scattering of the light in the tissue. At scattering coefficients found in human skin tissue [44, 51], for example, it is concluded that the maximum probing depth is independent of the focal length f. This is an important conclusion because the depth of focus and the lateral resolution of the OCT system may then be chosen independently of z max . For example, if no scanning of the focal plane in the tissue is desirable and, therefore, a large depth of focus has been chosen, the same maximum probing depth is obtained as for a system with a short depth of focus where the focal plane is scanned to keep it matched to the reference arm. This conclusion is not surprising or contrary to assumptions already held in the field. However, the theoretical analysis in this section provides a theoretical foundation for such statements. Moreover, this agreement may also be taken as a further validation of the OCT model presented here.
3.3 Doppler OCT Analysis
Noninvasive localization and measurement of blood flow is of great interest in many medical applications, e.g., ophthalmology, dermatology, and gastroenterology. Optical Doppler tomography (ODT) [52, 53] combines Doppler velocimetry and optical coherence tomography. Thus, ODT is feasible for noninvasive localized diagnostics of particle flow velocity in highly scattering media, and it is important for functional imaging. In contrast to conventional OCT, where the reflectivity profile of the sample is obtained by envelope detection of the interferometric signal, ODT employs coherent phase-sensitive demodulation of the heterodyne detector current to obtain depth profiles of blood flow velocity. Basically, depth-resolved velocity estimates are obtained directly from the corresponding mean [52, 53] or standard deviation [54, 55] of the observed Doppler-frequency spectrum.
In this section, the results of a theoretical analysis of ODT based on EHF with multiple-scattering effects included are presented. Experiments by Yazdanfar et al. [56] suggest the presence of multiple-scattering effects in ODT. Another study also confirmed the impact of multiple-scattering effects estimating the impact on the determination of flow parameters [57]. The purpose of the analysis below is to determine how multiple scattering affects the estimation of the depth-resolved localized flow velocity, i.e., to obtain the dependence of the mean and standard deviation of the Doppler-frequency spectrum on the scattering properties of the medium.
3.3.1 Multiple-Scattering Effects in ODT
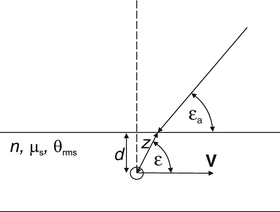
The ODT probe geometry being analyzed is shown in Fig. 3.6. In the absence of multiple scattering, and if the scattering geometry is precisely known, an estimate of the blood flow velocity at a given probing depth can be obtained as [52, 53]
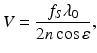
where λ 0 is the center wavelength of the light source, n is the index of refraction of blood, ε is the angle between the incident light and the direction of blood flow, and f S is the centroid frequency of each depth-resolved spectrum, which is used as a measure of the corresponding backscattered Doppler frequency.
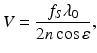
(3.32)

Fig. 3.6
The ODT probe geometry
In a multiple-scattering analysis of ODT, two effects must be taken into account: (a) the incident light on a moving particle contains a stochastic distribution of wave vectors at each optical frequency, and (b) in the round-trip propagation path to the backscattering event, the light will accumulate a random series of Doppler shifts due to the light being scattered by moving constituents along the path. Taking these multiple-scattering effects into account, the following equation for the mean Doppler shift may be derived [58]:
![$$ {\overline{f}}_D(d)=\frac{2n \cos \varepsilon }{\lambda_0}\left\{V(d) \exp \left(-\left\langle {\theta}^2\right\rangle /2\right)+\overline{V}(d)\left[1- \exp \left(-\left\langle {\theta}^2\right\rangle /2\right)\right]\right\}, $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ33.gif)
where 〈θ 2〉 = μ s zθ 2 rms. The quantities μ s and θ rms are the scattering coefficient and root-mean-square scattering angle of blood, respectively, and the probing depth z = d/sinε, where d is the transversal position in the vessel as indicated in Fig. 3.6. Furthermore, V(d) is the flow velocity as a function of the transversal position in the vessel, and  is the mean velocity of the flow along the propagation path to the probing depth z. If multiple-scattering effects are neglected, Eq. 3.33 reduces to Eq. 3.32 as expected. In addition, for a constant velocity profile where
is the mean velocity of the flow along the propagation path to the probing depth z. If multiple-scattering effects are neglected, Eq. 3.33 reduces to Eq. 3.32 as expected. In addition, for a constant velocity profile where 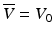 , Eq. 3.33 yields
, Eq. 3.33 yields 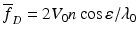 in agreement with Eq. 3.32, i.e., no multiple-scattering effects are present in this case as expected [59]. In the case of laminar flow in the vessel, the velocity and mean velocity profiles are given by [58]
in agreement with Eq. 3.32, i.e., no multiple-scattering effects are present in this case as expected [59]. In the case of laminar flow in the vessel, the velocity and mean velocity profiles are given by [58]
![$$ V(d)={V}_0\left[1-{\left(1-d/a\right)}^2\right]\kern0.56em \mathrm{f}\mathrm{o}\mathrm{r}\kern0.58em 0\le d\le 2a $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ34.gif)

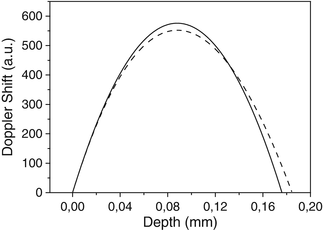
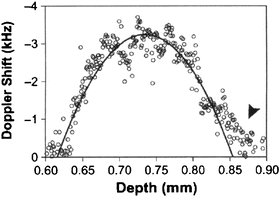
where a and V 0 are the radius of the vessel and the flow speed at the center of the vessel, respectively. In Fig. 3.7, the mean Doppler shift for laminar flow is shown with and without multiple-scattering effects included using Eqs. 3.33 and 3.32, respectively. The multiple scattering gives rise to a bias at the proximal end of the profile, which is in qualitative agreement with ODT measurements of a depth-resolved retinal flow profile obtained by Yazdanfar et al. [56] and shown in Fig. 3.8. Typical scattering parameters for blood [59] are used in Fig. 3.7 together with ODT system parameters and vessel diameter from Ref. [56]. The bias increases with larger μ s and θ rms (or smaller anisotropy factor). No such bias was predicted by Lindmo et al. [59] because of their neglect of the stochastic distribution of wave vectors incident on the backscattering particle.
![$$ {\overline{f}}_D(d)=\frac{2n \cos \varepsilon }{\lambda_0}\left\{V(d) \exp \left(-\left\langle {\theta}^2\right\rangle /2\right)+\overline{V}(d)\left[1- \exp \left(-\left\langle {\theta}^2\right\rangle /2\right)\right]\right\}, $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ33.gif)
(3.33)
 is the mean velocity of the flow along the propagation path to the probing depth z. If multiple-scattering effects are neglected, Eq. 3.33 reduces to Eq. 3.32 as expected. In addition, for a constant velocity profile where
is the mean velocity of the flow along the propagation path to the probing depth z. If multiple-scattering effects are neglected, Eq. 3.33 reduces to Eq. 3.32 as expected. In addition, for a constant velocity profile where 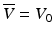 , Eq. 3.33 yields
, Eq. 3.33 yields 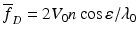 in agreement with Eq. 3.32, i.e., no multiple-scattering effects are present in this case as expected [59]. In the case of laminar flow in the vessel, the velocity and mean velocity profiles are given by [58]
in agreement with Eq. 3.32, i.e., no multiple-scattering effects are present in this case as expected [59]. In the case of laminar flow in the vessel, the velocity and mean velocity profiles are given by [58]![$$ V(d)={V}_0\left[1-{\left(1-d/a\right)}^2\right]\kern0.56em \mathrm{f}\mathrm{o}\mathrm{r}\kern0.58em 0\le d\le 2a $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ34.gif)
(3.34)

(3.35)


Fig. 3.8
Measurement of depth-resolved retinal flow profile taken (From Ref. [56]). The arrow indicates the effect of multiple scattering
Furthermore, the dependence of the standard deviation of the Doppler-frequency spectrum on the scattering properties of the flowing medium is also obtained. Thus, the following approximate expression of the standard deviation of the Doppler-frequency spectrum valid for all values of μ s z is obtained [58]:
![$$ \begin{array}{l}\Delta {f}_T(d)=\sqrt{\Delta {f}_D^2+\Delta {f}_{D0}^2}\\ {}\kern2.8em =\sqrt{\frac{V^2(d){n}^2{ \sin}^2\varepsilon }{\lambda_0^2}{\mu}_sz\kern0.1em {\theta}_{\mathrm{rms}}^2\left[2+p(d)\right]+\Delta {f}_{D0}^2}\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ36.gif)
where Δf D0 is the standard deviation of the Doppler-frequency spectrum in the absence of multiple scattering as reported previously in Ref. [55] and Δf D is the multiple-scattering contribution to the standard deviation of the ODT signal. The quantity p(d) is given by [58]
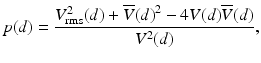
where V rms(d) is the root-mean-square velocity of the flow along the propagation path to the probing depth z and is given by [58]
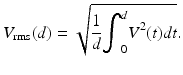
![$$ \begin{array}{l}\Delta {f}_T(d)=\sqrt{\Delta {f}_D^2+\Delta {f}_{D0}^2}\\ {}\kern2.8em =\sqrt{\frac{V^2(d){n}^2{ \sin}^2\varepsilon }{\lambda_0^2}{\mu}_sz\kern0.1em {\theta}_{\mathrm{rms}}^2\left[2+p(d)\right]+\Delta {f}_{D0}^2}\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ36.gif)
(3.36)
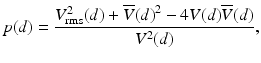
(3.37)
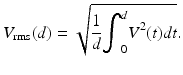
(3.38)
The standard deviation increases with larger μ s and θ rms (or smaller anisotropy factor). As expected, a multiple-scattering contribution to the standard deviation of the ODT signal is obtained, which is identically zero for a constant velocity profile. This is in contrast to the work by Lindmo et al. [59], who arrived at a nonzero contribution from multiple scattering for this case.
3.4 Advanced Monte Carlo Simulation of OCT Systems
In the present section, the derivation of a Monte Carlo (MC) model capable of dealing with the heterodyne detection scheme. Adequate MC modeling may serve as a numerical phantom for further theoretical studies in cases where analytical modeling may be cumbersome.
It is important to note that the MC method only describes the transport of energy packets along straight lines and therefore the approach is incapable of describing coherent interactions of light. These energy packets are often referred to as photon packets or simply photons, and this terminology is adopted here. However, it should be emphasized that no underlying wave equation is guiding or governing these photons. Accordingly, any attempt to relate these to real quantum mechanical photons should be done with great care as argued in Ref. [60] commenting on a suggested approach of including diffraction effects into MC simulations [61, 62]. An MC photon packet represents a fraction of the total light energy, and for some applications, especially continuous wave, it may be useful to think of the path traveled by a photon as one possible path in which a fraction of the power flows. A collection of photon packets may then be perceived as constituting an intensity distribution due to an underlying field, and it can, accordingly, seem tempting to infer behavior known to apply to fields upon photon packets. Consider, as an example, that one wishes to determine whether the photon packets are able to enter an optical fiber. It can then seem intuitively correct to restrict the access of photons impinging on the fiber end to those which fall within the numerical aperture of the fiber. However, such an angular restriction may not be correct, because the individual photon packet does not carry information of the entire field and its phase distribution. It is therefore impossible to determine whether a portion of the energy carried by a photon packet will enter the fiber due to a mode match between the fiber mode and the field underlying the collective intensity distribution of the photon packets. This discussion is treated in greater detail in Ref. [14].
With the above discussion of MC photons in mind, it may seem futile to investigate if MC simulation is applicable to estimate an OCT signal, which is the result of heterodyne mixing, and thus depends upon the coherence properties of the light. However, the problem may be reformulated to investigate whether or not the effect of the lack of coherence information in an MC simulation may be circumvented, or at least minimized. Others [63–66] have attempted to model similar optical geometries by interpreting the heterodyne process as a rejection process in which the detected photons must conform to a set of criteria on position and angle. Such a set of criteria is referred to as a detection scheme. However, these criteria were found by ad hoc considerations of the optical system, which may easily lead to incorrect results as exemplified above. Instead a mathematical derivation of the true criteria of the detection scheme will be given in the present section.
3.4.1 Theoretical Considerations
In the following, the EHF principle is used to derive an important result: an expression for the OCT signal depending on the intensity of the light only. This is obtained by calculating the mixing of the reference and sample beams in the plane conjugate to the plane in the sample probed by the system. The result is surprising, because the expression for the OCT signal depends on the coherence properties of the light [12]. However, it is shown that the formula used for calculating the OCT signal in this particular plane is mathematically identical to the result obtained in Ref. [12]. These results are valid for the, from a biomedical point of view, important case of a signal arising from a diffusely reflecting discontinuity embedded in a scattering sample. Note that this proves the viability of MC simulation to model the OCT technique, because it is shown that only intensity, and not field and phase, is necessary for this case.
The optical geometry of the sample arm is shown in Fig. 3.9, and it should be noted that the enclosed section corresponds to the geometry used for the EHF calculation in Sect. 3.2.2. An optical fiber end is positioned in the p-plane. The fiber emits a beam, which hits the collimating lens L1. The focusing lens L2 is positioned in the r-plane, and in this plane, the beam is a Gaussian beam with 1/e width, w 0, of the intensity. The beam is focused by L2 upon a diffusely reflecting discontinuity positioned at the depth z f inside a scattering sample a distance d from L2. The sample is taken to be a slab infinite in the transverse direction. The part of the light that is reflected from the discontinuity propagates out through the sample, through lenses L2 and L1 to the optical fiber, where it is collected. The lenses L1 and L2 have the focal length f and are taken to be identical, perfect, and infinite in radius. This means that the q– and p-planes are conjugate planes with magnification unity. The purpose of using the 4 F geometry is to have a physical representation of the conjugate plane to the probe plane. However, in Ref. [14] it is shown that the OCT signal term calculated from the conjugate plane is mathematically equivalent to the OCT signal calculated in the plane where the mixing physically takes place. Accordingly, the important result of Eq. 3.40 below is not restricted to the 4 F geometry. Hence, this proves the feasibility of using MC modeling in the analysis of OCT systems.
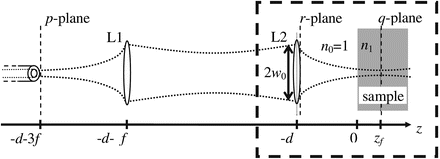

Fig. 3.9
Sample arm setup of the OCT system. The lenses L1 and L2 are considered to be identical, perfect, and have infinite radius. The setup is essentially a 4 F system (From Ref. [14])
The OCT signal is produced by the mixing of the light from the reference and sample arms on the photodetector of the OCT system. Due to the symmetry of the system, in Sect. 3.2.2 the EHF prediction of the mixing between signal and reference beam was conveniently calculated at the r-plane. The mean square of the signal current 〈i 2〉 is given by Eq. 3.9 and rewritten according to the notation in Fig. 3.9 to yield
![$$ \left\langle {i}^2(z)\right\rangle =2{\alpha}^2{\left|\gamma \left(\tau \right)\right|}^2\mathrm{R}\mathrm{e}\left[{\displaystyle \iint {\Gamma}_S\left({\mathbf{p}}_1,{\mathbf{p}}_2;z\right){\Gamma}_R\left({\mathbf{p}}_1,{\mathbf{p}}_2;z\right)}d{\mathbf{p}}_1d{\mathbf{p}}_2\right]\equiv {\Psi}_r\left\langle {i}_0^2\right\rangle, $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ39.gif)
where Γ R (r 1, r 2) = 〈U R (r 1)U R *(r 2)〉 = U R (r 1)U R *(r 2) is the cross correlation of the scalar reference field, Γ S (r 1, r 2) = 〈U S (r 1)U S *(r 2)〉 is the cross correlation of the sample field, and r 1 and r 2 are vectors in the r-plane; see Fig. 3.9. Ψ r is the heterodyne efficiency factor (defined in Eq. 3.17; subscript r refers to it being calculated in the r-plane), which quantifies the reduction in signal due to scattering, and 〈i 0 2〉 is the OCT signal current in the absence of scattering.
![$$ \left\langle {i}^2(z)\right\rangle =2{\alpha}^2{\left|\gamma \left(\tau \right)\right|}^2\mathrm{R}\mathrm{e}\left[{\displaystyle \iint {\Gamma}_S\left({\mathbf{p}}_1,{\mathbf{p}}_2;z\right){\Gamma}_R\left({\mathbf{p}}_1,{\mathbf{p}}_2;z\right)}d{\mathbf{p}}_1d{\mathbf{p}}_2\right]\equiv {\Psi}_r\left\langle {i}_0^2\right\rangle, $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ39.gif)
(3.39)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



![$$ \begin{array}{l}{\left\langle {i}^2(z)\right\rangle}_{coh\_ gate}\approx \frac{\alpha^2{P}_R{P}_s{\sigma}_b}{\pi {w}_{{}^{{}^H}}^2}\\ {}\kern2.28em \times \left[{e}^{-2{\mu}_sz}+\frac{4{e}^{-{\mu}_sz}\left(1-{e}^{-{\mu}_sz}\right)}{1+\frac{w_S^2}{w_H^2}}+{\left(1-{e}^{-{\mu}_sz}\right)}^2\frac{w_H^2}{w_S^2}\right]\\ {}\kern1.8em ={\left\langle {i}^2\right\rangle}_0\Psi (z).\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_4_Chapter_Equ18.gif)