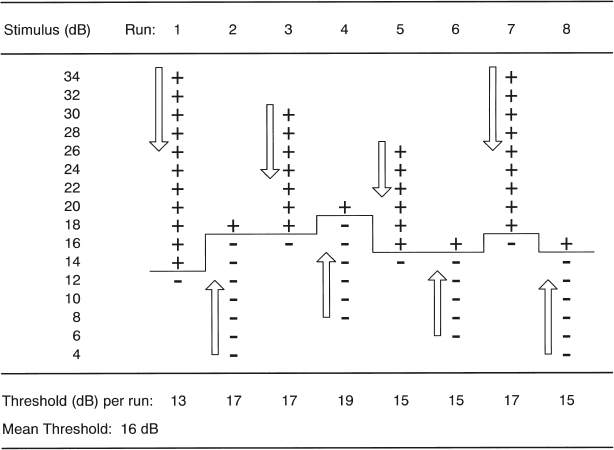
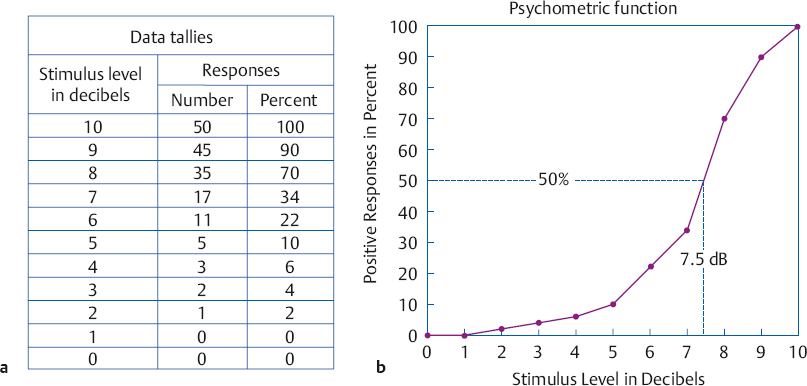
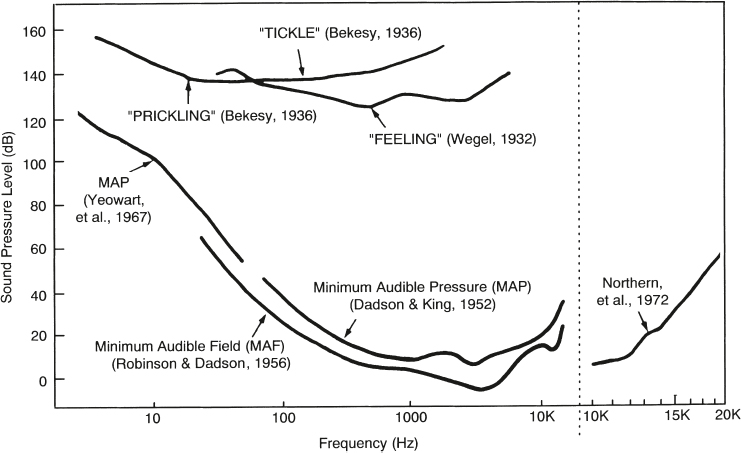
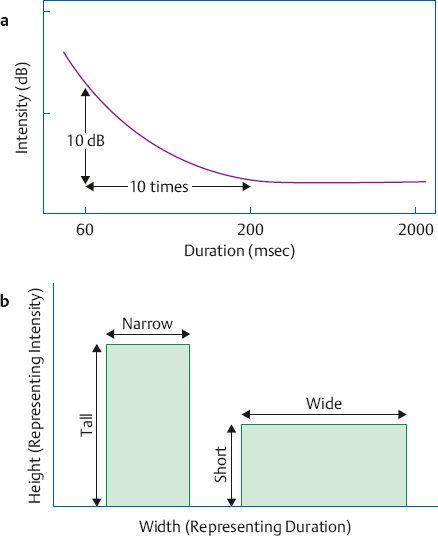
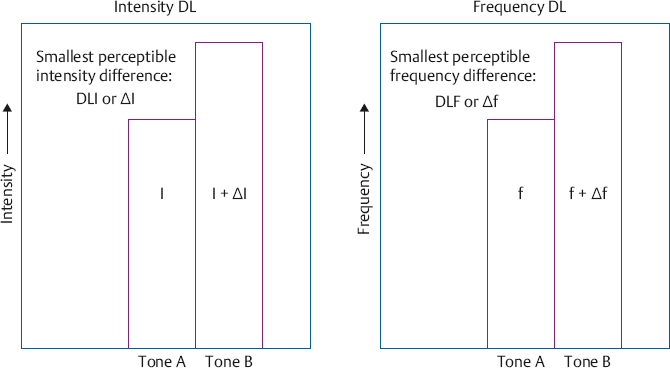
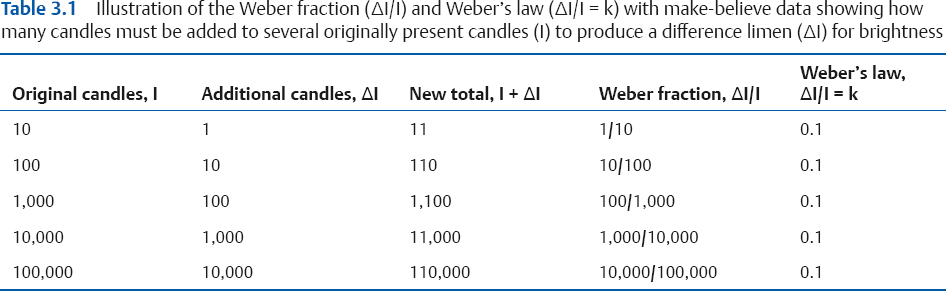
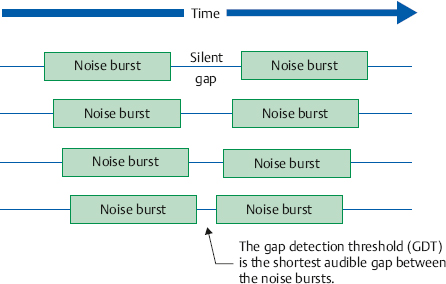
3 Measurement Principles and the Nature of Hearing

Most tests and other measures of hearing can be viewed in terms of the classic nominal, ordinal, interval, and ratio scales of measurement described by Stevens (1975). In a nominal scale, subjects or observations are simply categorized into different groups, but there is no order or hierarchy among the groups. Some examples include grouping people according to gender (male/female) or eye color (brown/blue/hazel), or classifying paintings by subject type (landscape/portrait/still life). On the other hand, if there is also some hierarchy or order among the observations or categories, then we have an ordinal scale. For example, we might ask subjects to specify their relative preferences for different kinds of paintings, or to organize the paintings according to relative price. Here, there is an orderly progression from group to group, but the spacing between groups is different. For example, several paintings might be rank ordered according to their prices, which are $10, $25, $100, $150, and $175. Because we know the relative order of the observations, the information on ordinal scales can be described in terms of medians and percentiles.

An ordinal scale becomes an interval scale when the spacing between categories or observations is equal, such as the hours on a clock or degrees of temperature in Fahrenheit or Celsius. Notice that the spacing is the same between any successive two points on the scale: There is 1 hour from 6 am to 7 am and there is also 1 hour from 10 pm to 11 pm; and there is one degree from 30°C to 31°C and also from 99°C to 100°C. An interval scale allows us to use most kinds of calculations so information can now be described in terms of means (averages) and standard deviations. However, ratios may not be used because there is no true zero point. Ratio scales have all the characteristics of interval scales plus a true zero point (an inherent origin). Length and temperature on the Kelvin scale (where 0 is absolute zero) are typical examples of ratio scales, as are loudness in sones and pitch in mels, described later in this chapter. All mathematical calculations can be used with ratio scale information, including the use of ratios, geometric means, and decibels.

The classical techniques that have been used to measure hearing and other senses are the methods of limits, adjustment, and constants (or constant stimuli). Other testing methods are also available, such as the direct scaling approaches (discussed below) as well as the clinical techniques (discussed later). Sophisticated adaptive testing methods (see, e.g., Gelfand, 1998) are usually employed in research applications, but they have clinical uses as well. We will describe each of the methods of limits, adjustment, and constants in the context of a test to find the subject’s threshold of hearing for a pure tone signal, which is simply the lowest intensity level at which the subject is able to hear. However, these methods can also be used for other kinds of measurements, such as determining the smallest perceptible difference in intensity or frequency between two sounds.

The method of limits is illustrated in Fig. 3.1. The subject is presented with one tone at a time, and he responds by indicating whether the stimulus was heard (“yes” or +) or not heard (“no” or –) after each presentation. The tester controls the level of the stimulus and changes it in fixed steps (e.g., 2 dB at a time) in one direction (ascending or descending) until the responses change from “yes” (+) to “no” (–), or from “no” (–) to “yes” (+). Each set of presentations is called a run. Eight runs are shown in the figure. Descending runs begin above the subject’s expected threshold, and the stimulus level is lowered until the tone first becomes inaudible. Ascending runs start below the subject’s threshold, and the level is raised until the tone is first heard. Notice that the crossover point varies from run to run, so the best estimate of the threshold is the average of several runs. Testing biases are minimized by averaging across an equal number of ascending and descending runs with different starting levels, as illustrated in the figure.

In the method of adjustment, the stimulus level changes continuously rather than in fixed steps, and is controlled by the subject herself. To find her threshold, the subject increases (or decreases) an unmarked level control until the tone first becomes audible (or inaudible). Bracketing, or increasing and decreasing the level alternately until a change point is reached, is a commonly employed modification of the methods of adjustment and limits.

The methods of limits and adjustment are sequential techniques because one presentation level depends on the response to the previous one. In contrast, the method of constant stimuli (constants) uses an equal number of stimuli at each of several predetermined levels, which are presented to the subject in random order. The “yes” (+) and “no” (–) responses are tallied for each of the levels used. The threshold is then obtained by calculating the level that corresponds to 50% from these tallies. Fig. 3.2 shows an example in which the percentage of “yes” (+) responses is calculated on the basis of 50 random tone presentations at 11 levels from 0 dB to 10 dB sound pressure level (SPL). The tallies are converted into percentages, which are then plotted on a graph known as a psychometric function. The 50% point on the psychometric function is usually considered to be the threshold, which corresponds to 7.5 dB in this example. The method of constants is very accurate, but it can be inefficient because many presentations are “wasted” at levels well above and well below the threshold (Fig. 3.2).

Direct Scaling

In direct scaling the subject directly establishes the correspondence between physical sounds and how they are perceived. The major approaches are partition scales and ratio or magnitude scales. The loudness (sone) and pitch (mel) scales discussed later in this chapter were developed using the magnitude and ratio scaling methods. With partition scales the subject is presented with a range of intensities or frequencies, and is asked to divide (partition) this range into equally spaced categories on the basis of how she perceives them.

Ratio scales are developed by ratio estimation or production. In ratio estimation the subject is presented with pairs of tones and describes (estimates) how they are related in the form of a ratio. For example, compared with the first one, the second tone might be twice as loud, half as loud, four times louder, etc.; or its pitch might be half as high, one-quarter as high, twice as high, etc. The opposite approach is ratio production. Here, the subject is asked to adjust (produce) the intensity of a tone until it sounds twice or half as loud as another tone, or to change the frequency of a tone so that its pitch is one-quarter, half, or twice that of another tone.

Magnitude scales are similar to ratio scales, except they use numbers (magnitudes) instead of ratios or fractions. In magnitude estimation the subject is presented with stimuli along a continuum (e.g., intensity) and is asked to assign numbers to each of them in a way that reflects the magnitude of the perception (e.g., loudness). The results show the relationship between physical stimuli and their perception, as in Fig. 3.3. There are two major variations of the magnitude estimation method. In one approach the subject is presented with a “standard” tone called a modulus and is told that it has a magnitude of, say, “10.” She then hears other tones at other intensities and is asked to describe (estimate) their magnitudes with numbers that are proportional to the modulus. A tone that is twice as loud as the modulus is rated 20; 40 means four times louder; and 2 means one-fifth as loud. The alternative approach is to omit the modulus. In this case the subject is asked to provide a rating for each sound using numbers that represent how they are perceived. Similar results are obtained with and without the modulus, as illustrated in the figure. The opposite of magnitude estimation is magnitude production. Here the subject is presented with numbers and must adjust the intensity (or frequency) to produce a tone with the corresponding loudness (or pitch).

Magnitude scales have been developed for a large number of sensations, and it is even possible to make cross-modality matches, that is, to express a perception from one sensory modality in terms of a different sense. Cross-modality matching can be useful audiologically by facilitating the ability to assess a patient’s perception of loudness in terms of perceived line length (Hellman & Meiselman 1988; Hellman 1999).

The Nature of Normal Hearing

Audiology is concerned with the normal and abnormal aspects of hearing, its place in the communicative process, and the clinical evaluation and management of patients with auditory impairments. The area of science that deals with the perception of physical stimuli is called psychophysics. Hence, in addition to being an aspect of audiology, the science that deals with perception of sound is also known as psychoacoustics.

The Range of Hearing

Minimal Audible Levels

It is useful to conceive of a range of hearing that includes sounds that are audible and tolerable. The lower curves in Fig. 3.4 show the faintest audible sounds or thresholds of normal people in decibels of sound pressure level (dB SPL) as a function of frequency. The striking feature of these curves is they are not flat. Instead, the SPL needed for a sound to be barely audible depends on its frequency to a major extent. Hearing thresholds are reasonably sensitive between ~ 100 and 10,000 Hz, and become poorer (i.e., more intensity is needed to reach threshold) as frequency increases and decreases above and below this range. In addition, hearing is most sensitive (i.e., the least amount of intensity is needed to reach threshold) in the 2000 to 5000 Hz range. The resonant responses of the conductive system are largely responsible for the lower thresholds in this most sensitive frequency range (see Chapter 2).

The sound levels needed to achieve minimum audibility also depend on how they are obtained. Notice that the curve labeled “MAF” is ~ 6 to 10 dB lower (i.e., better or more sensitive) than the curves labeled “MAP.” Minimal audible pressure (MAP) is based on monaural (one ear) thresholds that are obtained with earphones. First, the subject’s threshold is obtained with an appropriate method. Then the sound pressure that corresponds to that threshold is measured as it actually exists under the earphone in the subject’s ear canal. A commonly used alternative approach is to measure the sound in a 6-cc coupler, which is a special measurement cavity standardized for this purpose. We shall see that the latter method is used to calibrate audiological instruments. In contrast, minimal audible field (MAF) values are based on the binaural (two ear) thresholds of subjects listening to sounds presented from a loudspeaker in an echo-free (anechoic) room. After determining the threshold, the subject leaves the room and is replaced by a microphone that measures the sound as it exists in the same location previously occupied by the subject’s head.

The discrepancy between the MAF and MAP thresholds has been known as the “missing 6 dB,” and was a problematic issue for quite some time. However, it appears that the MAF-MAP difference is more apparent than real because it is accounted for by a combination of factors, including binaural versus monaural hearing, physiologic noise that masks stimuli presented under earphones, real ear versus coupler measurements, and other technical factors (Killion 1978).

Upper Limits of Hearing

The upper levels of usable hearing depend on how they are defined. The threshold of uncomfortable loudness occurs at ~ 100 dB SPL (Hood & Poole 1970; Morgan, Wilson, & Dirks 1974), although higher values of ~ 111 to 115 dB SPL have been reported by Sherlock and Formby (2005). However, the threshold is much higher for sensations such as feeling, tickle, and pain. These unpleasant and potentially intolerable sensations are generally tactile rather than auditory in nature, and occur roughly between 120 and 140+ dB SPL, depending on the nature of the sensation. Several examples are shown in Fig. 3.4. In contrast to the threshold sensitivity curves, the upper limits of hearing are relatively flat across the frequency range for both uncomfortable loudness and tactile sensations.

Temporal Summation

The threshold for a sound is not affected by its duration unless it becomes shorter than approximately one third of a second. When a sound is shorter than ~ 300 milliseconds, then its threshold increases when its duration decreases, and vice versa (Fig. 3.5a). In general, a ten-times increase in duration can be offset by a 10 dB decrease in intensity, and a 10-times (or decade) decrease in duration can be offset by a 10 dB increase in intensity. This phenomenon is called temporal summation or temporal integration. An example of this time-intensity trade is as follows: Suppose a person’s threshold is 18 dB for a tone that is 250 milliseconds long. If we reduce the duration of the tone by 10 times, to only 25 milliseconds, then the person’s threshold will increase by 10 dB to 28 dB. Similarly, if the threshold of a tone lasting 25 milliseconds is 28 dB, then increasing its duration by 10 times, to 250 milliseconds, will cause the threshold to improve by 10 dB to 18 dB. The same relationship also applies to the loudness of a sound; for example, a 40 dB tone lasting 25 milliseconds will sound as loud as a 50 dB tone if increase its duration by 10 times, to 250 milliseconds.

Temporal summation reflects the ear’s ability to integrate energy within a time frame of roughly one third of a second. The principle is illustrated in Fig. 3.5b, where the area of each rectangle represents the amount of energy present. Notice that the area (energy) is the same regardless of whether the rectangle is (1) high and narrow (representing more intense and shorter in duration) or (2) short and wide (representing less intense and longer in duration). Students with photographic experience will recognize that this phenomenon is similar to the trade-off between lens opening and shutter speed.

Differential Sensitivity

The smallest perceptible difference between two sounds is called a difference limen (DL) or the just noticeable difference (jnd). For example, the smallest intensity difference that can be distinguished between two sounds is the DL for intensity. Because delta (Δ) is the symbol for “change,” the intensity DL is often called ΔI. If ΔI is the intensity difference needed to tell two sounds apart, then one of those sounds has an intensity of I and the other one has an intensity of I + ΔI (Fig. 3.6). Analogous terms apply to just noticeable differences for other aspects of sounds. For example, the difference limen for frequency, Df, is the smallest discernible difference between the frequencies of two sounds, f and f + Df.

The values of ΔI and Df are absolute difference limens because they specify the actual physical difference needed to tell two sounds apart. However, common experience tells us that the physical size of a DL is not the same under all conditions. For example, we all know that the additional illumination provided by a tiny night-light is very noticeable in the dark of night but is totally indiscernible during the day. In other words, the size of ΔI depends on the size of I. For this reason, we are especially interested in the relative difference limen that considers both the DL as well as the starting value. The relative DL is equal to ΔI/I and is called the Weber fraction. The notion that the Weber fraction (ΔI/I) is a constant value (k) is called Weber’s law. In numerical terms, Weber’s law says that ΔI/I = k.

These principles become clear when we consider a classic, albeit hypothetical, experiment described by Hirsh (1952) aimed at answering the question: “If we already have a certain number of candles, how many more candles must be added in order for us to notice a difference in brightness?” The “results” are given in Table 3.1. The first column gives the original numbers of candles (I), which might be 10, 100, 1000, 10,000, or even 100,000. The additional candles needed to tell a difference (the DL or ΔI) in each case are in the second column, and the new totals (I + ΔI) are in the third column. The fourth column, labeled “Weber fraction,” shows the raw ratios of ΔI/I in each case, and the last column, labeled “Weber’s law,” shows the results of simplifying each of these fractions. The results are obvious: the more candles you start with (I), the more candles you must add (ΔI) to tell a difference, but the relative size of the increase (ΔI/I) is always the same (ΔI/I = k = 0.1).

Difference Limens for Intensity and Frequency

Although the relative difference limen for intensity follows Weber’s law for white noise (e.g., Houtsma, Durlach, & Braida 1980), the value of ΔI/I improves to some extent with increasing sensation level for pure tones (e.g., Jesteadt, Wier, & Green 1977). Sensation level (SL) is simply the number of decibels above threshold, so that 0 dB SL means “at threshold” and 40 dB SL means 40 dB above threshold. For example, Jesteadt et al (1977) found the values of ΔI/I are roughly 0.4 near threshold, 0.3 at 40 dB SL, 0.2 at 60 dB SL, and somewhat smaller at high intensities. Hence, there appears to be a “near miss to Weber’s law” for the intensity difference limen in the sense that ΔI/I is not quite constant. The size of ΔI/I appears to be reasonably constant in the middle frequencies, but it is not clear whether this holds true for all audible frequencies.

The difference limen for frequency becomes larger (wider) as frequency increases and also as sensation level decreases (Wier, Jesteadt, & Green 1977). At the readily audible and comfortable level of 40 dB SL, the size of Df is ~ 1 Hz at 200 Hz and 400 Hz, and 2 Hz at 1000 Hz, 3 Hz at 2000 Hz, 16 Hz at 4000 Hz, and 68 Hz at 8000 Hz. In terms of the Weber fraction, Df/f is smallest (~ 0.002) between 600 Hz and 2000 Hz, and gets larger for the frequencies below and above this range. All of these values become larger (poorer) as the intensity decreases toward threshold.

Temporal Discriminations

The closest analogy in the time domain to the intensity and frequency DLs just discussed would be the difference limen for signal duration. Here the subject must determine which one of two signals lasted for a longer period of time. The difference limen for duration (Dt) becomes larger (longer) as the overall duration of the signal (t) increases, and the Weber fraction, Dt/t, is not constant (Abel 1972; Dooley & Moore 1988). However, this is by no means the only kind of time-related discrimination in hearing.

The shortest perceptible time interval or temporal resolution is typically on the order of 2 to 3 milliseconds in young, normal individuals, and can be measured by gap detection as well as other approaches (e.g., Fitzgibbons & Wightman 1982; Buus & Florentine 1985; Green 1985; Fitzgibbons & Gordon-Salant 1987). The stimulus used for gap detection testing is usually a pair of noises that are presented in rapid succession, separated by a very short break or gap. The duration of this gap is varied according to an appropriate method of measurement, and the subject’s task is to determine whether a gap can or cannot be heard. The shortest discernible gap is the gap detection threshold. These principles are illustrated in Fig. 3.7. The same results are obtained if the subject is asked whether she heard one continuous sound or two of them in succession. However, an interval of ~ 20 milliseconds is needed if the subject must indicate which of two distinguishable signals came first, or the perceived order (Hirsh 1959).

Loudness and Pitch

Loudness and pitch refer to how we perceive the physical attributes of intensity and frequency, respectively. It may seem odd to make this distinction since everyone knows sounds with greater intensities are louder than sounds with smaller intensities, and higher frequencies have higher pitches. These generalities are true. However, we will see that there is far from a one-for-one relationship between the perceptual world of loudness and pitch and the physical world of intensity and frequency.

Loudness Level

We have already seen that sounds of different frequencies are not equally audible (Fig. 3.4). In other words, different SPLs are needed to reach threshold at different frequencies; for example, 10 dB SPL may be audible at one frequency but not at another frequency. The same thing applies to loudness: even though tone A and tone B have the same intensity, one of them is likely to be louder than the other. In other words, loudness depends on frequency. We may now ask how much intensity is needed at each of two different frequencies for one tone to be perceived just as loud as the other tone. For example, how many decibels would it take for a 100 Hz tone to sound equally loud as a 1000 Hz tone at 40 dB SPL? To answer this question we may present a 1000 Hz tone at 40 dB alternately with various levels of a 100 Hz tone, and ask the subject whether each 100 Hz tone is louder, softer, or equally loud as the 1000 Hz reference tone. Alternatively, we might have the subject adjust the level of a 100 Hz tone until it sounds just as loud as a reference tone of 1000 Hz at 40 dB. The same procedure would then be repeated with other frequencies until we have developed a list of the SPLs at many different frequencies that all sound equally loud as the 40 dB, 1000 Hz tone. It makes sense that if all of these sounds are equally loud as the 1000 Hz, 40 dB reference tone, then they are also equal in loudness to each other. We could then plot these equally loud SPLs as a function of frequency, and draw a smooth line through them.

Stay updated, free articles. Join our Telegram channel

Join