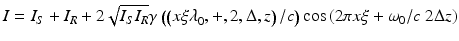Fig. 12.1
The four fundamental implementations of OCT
FD- and SS-OCT offer superior sensitivity and signal-to-noise ratio (SNR) over time-domain and linear OCT. But they also have some disadvantages. FD-OCT needs high performance optics for the spectrometer, SS-OCT is based on sophisticated rapidly tunable light sources, and the necessary Fourier transform requires some processing power. Additionally, the correlation of the reflectivity distribution in the sample, which is incorporated in the FD- and SS-OCT signals, may obscure the image. This is especially the case when strong reflecting surfaces are present in the image. By their working principle, TD-OCT and L-OCT avoid the autocorrelation problem and give unique information about the structure of the sample.
One of the main technological challenges for TD-OCT was to build an optical delay line that worked at high frequencies with a constant velocity [5], and still the delay line is an important factor that limits the acquisition speed and makes TD-OCT systems complex and sensitive to unwanted changes of the alignment. Obviously, TD-OCT without moving parts would be of great advantage, especially for commercial systems.
Linear OCT, which combines the principle of TD-OCT with a parallel detection scheme, is a way to overcome these limitations by projecting the interference pattern on a line detector. A problem of L-OCT was the high number of pixels which were needed to sample the interference pattern without aliasing. At a wavelength of 800 nm a ranging depth of 2 mm required at least 10,000 pixels. This problem was overcome by optically reducing the fringe frequency of the interference pattern without influencing the information-carrying parts. The advances in CCD and CMOS detector technology in the recent years made linear OCT devices possible.
This chapter describes theory, implementation, and performance of linear OCT systems and discusses possible applications. Line-field versions of linear OCT are briefly introduced.
12.2 Theory
12.2.1 The Principle of Linear OCT
The depth z s of reflecting or scattering tissue structures can be measured by interferometry because the propagation time of radiation with a frequency ω travelling through tissue with a phase velocity c introduces a phase shift of Φ S = (ω/c) z S . In OCT this phase shift is recovered by superposing the radiation from the sample with a reference beam. With the electric fields for sample and reference radiation given by 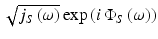 and
and  , respectively, the intensity of the interference signal on a detector at the output of the interferometer results in
, respectively, the intensity of the interference signal on a detector at the output of the interferometer results in

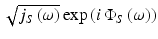 and
and  , respectively, the intensity of the interference signal on a detector at the output of the interferometer results in
, respectively, the intensity of the interference signal on a detector at the output of the interferometer results in
(12.1)
ΔΦ = Φ S − Φ R = ω/c (2z S − 2z R ) is the phase difference between sample and reference irradiation. For monochromatic light the interference signal I changes periodically with the difference Δz = z S − z R of the path lengths in sample and reference arm and gives no unique information for a Δz larger than the half of the wavelength λ. Therefore, OCT uses polychromatic light to recover Δz. The phase difference and subsequently the interference pattern are dependent on the frequency of the radiation. Hence the change of ΔΦ with the frequency contains in a unique way the depth information. In TD- and L-OCT a nearly zero phase difference is detected by superposing all frequency components on the detector. This is described mathematically by integrating Eq. 12.1 over the whole frequency range of the radiation.
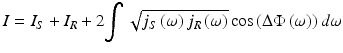
I s and I R are the integrals over spectral densities j s and j R which yield the intensities for reference and sample radiation. When the dispersions in both arms of the interferometer are balanced, the interference signal consists of a harmonic function with the central frequency ω 0, which is modulated by the Fourier transform 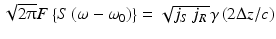 of the radiation spectrum s(ω) [6]:
of the radiation spectrum s(ω) [6]:
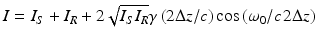
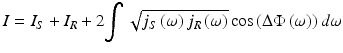
(12.2)
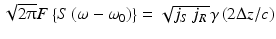 of the radiation spectrum s(ω) [6]:
of the radiation spectrum s(ω) [6]: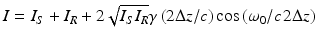
(12.3)
The modulation of the cosine actually contains the normalized coherence function γ of the radiation source. The interference pattern is only observed if the difference of the optical path lengths 2Δz/c is within the width of the coherence function γ. This coherence gate allows to separate the signals from different depths in the sample by evaluating I, while the optical delay in one arm of the interferometer is changed over a certain range.
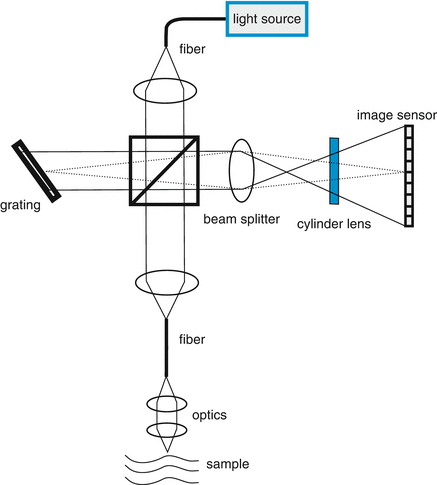
In linear OCT the interference pattern is measured in parallel by spatially extending the interference pattern on a line or array detector (Fig. 12.2). A simple way for this is to expand sample and reference beam and superpose them under the angles β s and β R on the detector (see inset in Fig. 12.2).


Fig. 12.2
The basic principle of linear OCT (L-OCT). An interference pattern is formed on the image sensor by the tilted sample and reference beams
In that case, the phases of both beams depend linearly on the lateral position on the detector and the resulting phase difference is given by
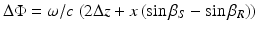
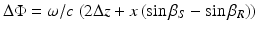
(12.4)
The interference pattern now contains the carrier frequency ξ = (sin β S − sin β R )/λ 0, which can be controlled by the incidence angles of both beams. Without moving parts a whole A-scan can be measured.
The time-dependent modulation of a signal from a single point detector at the output of the interferometer is exchanged by the measurement of a spatial intensity distribution with an extended detector. Differences in the performance and layout between TD-OCT and L-OCT arise, therefore, only from the parallel acquisition of data for the complete A-scan, the discrete sampling of the interference pattern, and the performance characteristics of the different classes of detectors used.
One important restriction for L-OCT is that the pixel frequency ξ P of the detector has to be at least two times the modulation frequency ξ to fulfill the Nyquist criterion. Since a full cycle of the interference signal corresponds to a path length difference of λ/2, at least 4Δd/λ pixels are needed for a certain measurement depth Δd. Hence, the depth range is limited by the number of available pixels. The information that is detected by OCT has a bandwidth that is the reciprocal of the coherence length lc (typically 5–20 μm), which is significantly smaller than ξ. To reduce the number of necessary pixels, it would be desirable to reduce the bandwidth of the interference pattern by reducing or removing the carrier frequency ξ. In fact there is the possibility of an optical control of the carrier frequency without loss of information.
12.2.2 Optical Control of the Carrier Frequency
12.2.2.1 Transmission Grating in Near Field
In radio technology, a reduction of the carrier is often done by mixing, i.e., the multiplication with a second fixed frequency. Optically, this can be facilitated by the transmission of the interference pattern through a mask with a periodically changing absorption, i.e., by a transmission grating (Fig. 12.3). The intensity directly behind the grating is the product of the interference pattern with the transmission of the mask. With a grating of a frequency ξ g and a harmonic transmission τ = (1 + cos(2πξ g x))/2, the following intensity pattern results to [7].
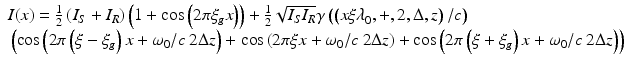

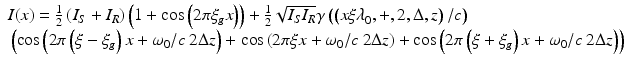
(12.6)

Fig. 12.3
Reduction of the fringe frequency of the interference pattern by a periodic transmission grating
I(x) now consists of four bands with the center frequencies at ξ − ξ g , ξ g , ξ, and ξ + ξ g . All frequency components but ξ g are modulated by the information from the sample. With choosing ξ g and ξ in a way that ξ − ξ g is below the half sampling frequency and that ξ and ξ + ξ g are above the pixel frequency ξ P , the Nyquist criterion can be fulfilled and the high-frequency components of the interference pattern will be averaged out on the light-sensitive area of the pixels [7]. Only the signal component 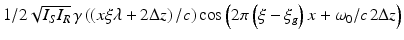 and a constant background will be measured. The spectral components of the coherence function γ and, therefore, the structure information of the sample are not affected by the transmission mask.
and a constant background will be measured. The spectral components of the coherence function γ and, therefore, the structure information of the sample are not affected by the transmission mask.
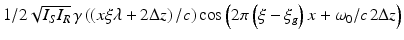 and a constant background will be measured. The spectral components of the coherence function γ and, therefore, the structure information of the sample are not affected by the transmission mask.
and a constant background will be measured. The spectral components of the coherence function γ and, therefore, the structure information of the sample are not affected by the transmission mask.By this principle, the carrier frequency can be reduced to any value. If ξ g is exactly ξ, the carrier is completely removed, and only the modulation multiplied by a phase term will appear on the sensor. In this case the intensity on the detector becomes sensitive to the relative phase between reference and sample irradiation which modulates the signal between zero and the maximal level. The simplest way to avoid the resulting ambiguity is to use a low-frequency carrier. For a reconstruction of γ, two cycles of the carrier per coherence length l c are sufficient. Without transmission mask l c /λ cycles, which appear under γ, have to be sampled. Therefore, at a fixed number of pixels the grating increases the image depth by a factor of l c /2λ. At 800 nm wavelength and 15 μm coherence length, this is about an order of magnitude. Unfortunately the mask reduces the signal due to transmission losses of the grating and the fact that 50 % of the signal power is mixed into the sum frequency where it cannot be detected. The modulation amplitude of the signal is thereby reduced to 25 % compared to L-OCT without transmission mask.
12.2.2.2 Diffraction by a Phase Grating
A control of the fringe frequency of the interference pattern with minimal signal loss is possible by the use of a phase grating. In a beam diffracted by a grating, parallel light rays, which emerge from each groove, have different propagation times. The direction of the newly formed phase front, which determines the carrier frequency in the interference pattern, is decoupled from the group front (the time delay of wave packages), which determines the width of the coherence function (Fig. 12.4). An individual control of the group and phase delay across the beam diameter is therefore possible by a phase grating. This principle, which was used for femtosecond pulse measurements [8, 9], in delay lines for TD-OCT [10, 11], and for coherent microscopy [12], can also be applied to L-OCT [13].
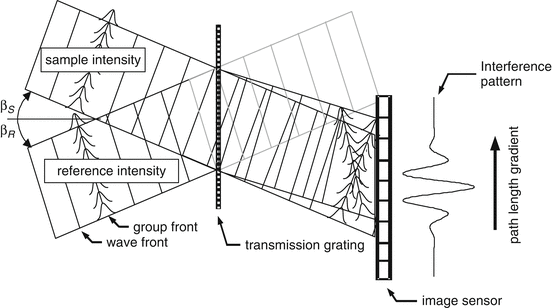

Fig. 12.4
Reduction of the fringe frequency by a diffraction grating. A grating forms new phase fronts in the diffracted beam, in which the propagation time varies across the diameter. Phase and group fronts are tilted against each other
A reduction of the fringe frequency occurs when different diffraction orders of the reference and sample beam are superposed on the detector (Fig. 12.4). The m th diffraction order introduces an achromatic phase shift of 2πm between parallel rays from neighbored grating lines. Therefore, a phase which varies by 2π m ξ g x is introduced across the beam. This phase term changes Eq. 12.3 to
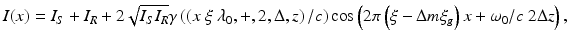
where Δm is the difference of the diffraction orders of the sample and reference beam which interfere on the detector. Compared to Eq. 12.5, an expression appears, in which the fringe frequency is reduced by Δm times the grating frequency ξ g . In contrast to the transmission mask, only the term with the difference frequency appears, and the losses in the sample beam can be kept small by adequate design. In the configuration of Fig. 12.4, a low diffraction efficiency of the grating causes only negligible losses to the sample beam. The high losses to the reference beam can be tolerated, because only the intensity from the sample is affecting the sensitivity of the system. Therefore, with a phase grating a control of the fringe frequency is possible without compromising the sensitivity of the OCT signal. With an additional beam splitter, a reflection grating can be used as well (Fig. 12.5). An open Michelson interferometer, in which the reference mirror is replaced by a grating in Littrow configuration, offers here an elegant way [14, 15]. The carrier frequency is adjusted by the angle between reference and sample beam. The path length difference over the detector is determined by the tilt angle of the grating.
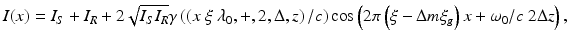
(12.7)

Fig. 12.5
Reduction of the fringe frequency by a reflection grating
12.2.3 Sensitivity and Signal-to-Noise Ratio (SNR)
In principle L-OCT can reach the same sensitivity and signal-to-noise ratio (SNR) as T-OCT [16]. According to Eq. 12.3 the OCT signal S, which shall reflect the intensity of the radiation scattered by tissue structures, is calculated as the square of the detected modulation integrated over the coherence function γ.
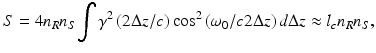
where n R and n S are the numbers of photoelectrons generated by the reference and the sample radiation, respectively. Noise arises from the shot noise mainly generated by the constant background signal n B in the interference pattern and the noise n D of the detector and electronics.
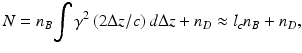
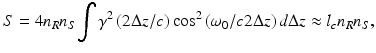
(12.8)
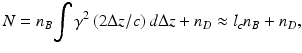
(12.9)
For small signal intensities (the reference intensity is much larger than the sample intensity) and quantum noise limited performance (detector noise is smaller than shot noise), n B is given by n R and the SNR is just the number n S of detected photons from the sample. n S can be expressed by the intensity I s received from the sample, the exposure time τ, and the quantum efficiency η of the detector:


(12.10)
Besides the power I S from the sample, also the ratio between coherence length l c and measuring range Δd determines the SNR, because I S , which is spread over the whole detector length, only contribute to the signal n s within the window of the coherence function γ. This fraction can be approximated by l c /Δd. A similar equation is obtained for TD-OCT systems. In FD- and SS-OCT the SNR is higher by the factor Δd/l c , because the sample intensities from all depth contribute to the signal in every pixel of the detector [3]. Hence, the number of signal photons n s is only given by I s τη/ℏω.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree