and 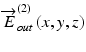 , which correspond to two different incident polarization states,
, which correspond to two different incident polarization states, 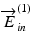 and
and 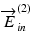 , where x, y is the transversal position and z is the position in depth. The Jones vectors of
, where x, y is the transversal position and z is the position in depth. The Jones vectors of 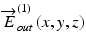 and
and 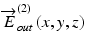 are measured by a polarization-diversity OCT detection scheme, by which two OCT images of two orthogonal polarization components, typically the horizontal and vertical components, are obtained. One of the OCTs represents the first entry of the Jones vector, and the other represents the second entry. The details of the polarization-diversity detection are described in Sect. 35.3.2. Owing to the three-dimensional resolution of OCT,
are measured by a polarization-diversity OCT detection scheme, by which two OCT images of two orthogonal polarization components, typically the horizontal and vertical components, are obtained. One of the OCTs represents the first entry of the Jones vector, and the other represents the second entry. The details of the polarization-diversity detection are described in Sect. 35.3.2. Owing to the three-dimensional resolution of OCT, 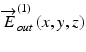 and
and 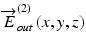 are spatially resolved, that is, they are functions of space, while the incident polarization states
are spatially resolved, that is, they are functions of space, while the incident polarization states 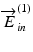 and
and 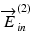 are constants.
are constants.
By denoting a Jones matrix of interest as J(x, y, z), the Jones vectors of incident and backscattered light are associated as
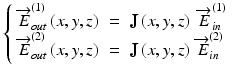
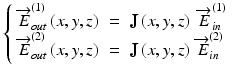
(35.1)
This set of equations corresponds to two measurements of OCT with different incident polarization states. By calculating ![$$ {\overrightarrow{E}}_{out}^{(1)}\left(x,y,z\right)\;\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \end{array}\right]+{\overrightarrow{E}}_{out}^{(2)}\left(x,y,z\right)\;\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_IEq11.gif) , these two equations are unified as
, these two equations are unified as

where E out (x, y, z) and E in are the Jones vector matrices of ![$$ {\mathbf{E}}_{out}\left(x,y,z\right)\equiv \left[\begin{array}{cc}\hfill {\overrightarrow{E}}_{out}^{(1)}\left(x,y,z\right)\hfill & \hfill {\overrightarrow{E}}_{out}^{(2)}\left(x,y,z\right)\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_IEq12.gif) and
and ![$$ {\mathbf{E}}_{in}\equiv \left[\begin{array}{cc}\hfill {\overrightarrow{E}}_{in}^{(1)}\hfill & \hfill {\overrightarrow{E}}_{in}^{(2)}\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_IEq13.gif) . By using Eq. 35.2, the spatially resolved Jones matrix, i.e., Jones matrix tomography, is obtained from the measured Jones vectors matrix E out (x, y, z) and predefined Jones vectors matrix E in as
. By using Eq. 35.2, the spatially resolved Jones matrix, i.e., Jones matrix tomography, is obtained from the measured Jones vectors matrix E out (x, y, z) and predefined Jones vectors matrix E in as
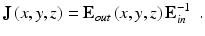
![$$ {\overrightarrow{E}}_{out}^{(1)}\left(x,y,z\right)\;\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \end{array}\right]+{\overrightarrow{E}}_{out}^{(2)}\left(x,y,z\right)\;\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_IEq11.gif) , these two equations are unified as
, these two equations are unified as
(35.2)
![$$ {\mathbf{E}}_{out}\left(x,y,z\right)\equiv \left[\begin{array}{cc}\hfill {\overrightarrow{E}}_{out}^{(1)}\left(x,y,z\right)\hfill & \hfill {\overrightarrow{E}}_{out}^{(2)}\left(x,y,z\right)\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_IEq12.gif) and
and ![$$ {\mathbf{E}}_{in}\equiv \left[\begin{array}{cc}\hfill {\overrightarrow{E}}_{in}^{(1)}\hfill & \hfill {\overrightarrow{E}}_{in}^{(2)}\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_IEq13.gif) . By using Eq. 35.2, the spatially resolved Jones matrix, i.e., Jones matrix tomography, is obtained from the measured Jones vectors matrix E out (x, y, z) and predefined Jones vectors matrix E in as
. By using Eq. 35.2, the spatially resolved Jones matrix, i.e., Jones matrix tomography, is obtained from the measured Jones vectors matrix E out (x, y, z) and predefined Jones vectors matrix E in as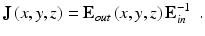
(35.3)
Since this equation contains the inverse matrix of E in , E in should be a non-singular matrix. In other words, the two incident light beams should not be parallel, namely, 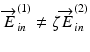 , where ζ is an arbitrary complex constant.
, where ζ is an arbitrary complex constant.
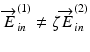 , where ζ is an arbitrary complex constant.
, where ζ is an arbitrary complex constant.As represented by Eq. 35.3, the basic principle of Jones matrix OCT is very simple. However, there are still fundamental issues such as the effect of birefringence of the OCT system and the determination of E in . The following section describes an extended principle of Jones matrix OCT by which the system birefringence is canceled. In addition, the extended principle enables a determination of J(x, y, z) without any knowledge of E in .
35.2.2 Extended Principle of Jones Matrix Optical Coherence Tomography
The Jones vectors of incident and backscattered light in the previous section had been defined at just before and after the sample. However, in general, the optical components utilized in OCT have specific polarization properties. In particular, optical fiber, which is commonly utilized in an OCT interferometer, has birefringence, and this fiber birefringence is altered by several factors including mechanical stress and temperature. Hence, especially with single-mode fiber-based Jones matrix OCT, it is rarely possible to determine the Jones vector of the real incident light to the sample and also to measure the Jones vector of the backscattered light.
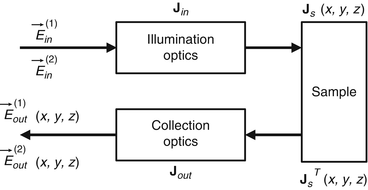
To first mathematically describe this issue and then provide its solution, we introduce a modified model of the Jones matrix measurement. Figure 35.1 shows a simplified schematic Jones matrix measurement by Jones matrix OCT. J in and J out represent Jones matrices of illumination and collection optics that may include the optical fiber, and J s (x, y, z) is a single-trip Jones matrix of a sample. Note that, in this scheme, 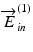 ,
,  and
and 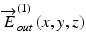 ,
, 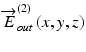 are the Jones vectors of the light incident to and output from the system, respectively, not to and from the sample. The incident point can be arbitrarily defined and does not affect the final measurement results except for axis orientation as discussed later in this section. The output polarization is typically defined as that at a detection unit.
are the Jones vectors of the light incident to and output from the system, respectively, not to and from the sample. The incident point can be arbitrarily defined and does not affect the final measurement results except for axis orientation as discussed later in this section. The output polarization is typically defined as that at a detection unit.
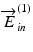 ,
,  and
and 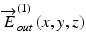 ,
, 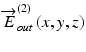 are the Jones vectors of the light incident to and output from the system, respectively, not to and from the sample. The incident point can be arbitrarily defined and does not affect the final measurement results except for axis orientation as discussed later in this section. The output polarization is typically defined as that at a detection unit.
are the Jones vectors of the light incident to and output from the system, respectively, not to and from the sample. The incident point can be arbitrarily defined and does not affect the final measurement results except for axis orientation as discussed later in this section. The output polarization is typically defined as that at a detection unit.
Fig. 35.1
A conceptual scheme of polarization properties of Jones matrix OCT. 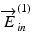 and
and 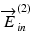 are the Jones vectors of the incident light to the OCT system,
are the Jones vectors of the incident light to the OCT system, 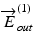 and
and 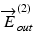 are the those of output light from the system, J in and J out are Jones matrices of illumination and detection optics, and J s is a single-trip Jones matrix of the sample
are the those of output light from the system, J in and J out are Jones matrices of illumination and detection optics, and J s is a single-trip Jones matrix of the sample
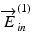 and
and 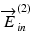 are the Jones vectors of the incident light to the OCT system,
are the Jones vectors of the incident light to the OCT system, 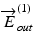 and
and 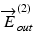 are the those of output light from the system, J in and J out are Jones matrices of illumination and detection optics, and J s is a single-trip Jones matrix of the sample
are the those of output light from the system, J in and J out are Jones matrices of illumination and detection optics, and J s is a single-trip Jones matrix of the sampleIn this scheme, the entire Jones matrix of the system and the sample becomes
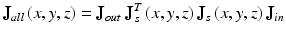
where J s T J s is a round-trip Jones matrix of the sample [32]. According to the similar discussion with Sect. 35.2.1, J all , ![$$ {\mathbf{E}}_{in}\equiv \left[\begin{array}{cc}\hfill {\overrightarrow{E}}_{in}^{(1)}\hfill & \hfill {\overrightarrow{E}}_{in}^{(2)}\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_IEq23.gif) and
and ![$$ {\mathbf{E}}_{out}\equiv \left[\begin{array}{cc}\hfill {\overrightarrow{E}}_{out}^{(1)}\hfill & \hfill {\overrightarrow{E}}_{out}^{(2)}\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_IEq24.gif) are associated as
are associated as
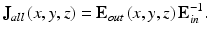
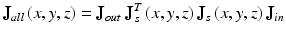
(35.4)
![$$ {\mathbf{E}}_{in}\equiv \left[\begin{array}{cc}\hfill {\overrightarrow{E}}_{in}^{(1)}\hfill & \hfill {\overrightarrow{E}}_{in}^{(2)}\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_IEq23.gif) and
and ![$$ {\mathbf{E}}_{out}\equiv \left[\begin{array}{cc}\hfill {\overrightarrow{E}}_{out}^{(1)}\hfill & \hfill {\overrightarrow{E}}_{out}^{(2)}\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_IEq24.gif) are associated as
are associated as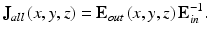
(35.5)
Note that the output Jones vector matrix E out (x, y, z) can be measured and the incident polarization state E in is arbitrarily selected.
The objective of the Jones matrix OCT measurement is to determine the phase retardation, diattenuation, and optic-axis orientation of the round-trip Jones matrix of the sample J s T (x, y, z) J s (x, y, z). For this purpose, J s T (x, y, z) J s (x, y, z) or its similar matrix should be obtained. This similar matrix at a position of (x, y, z) can be obtained by using J all (x, y, z) and J all (x, y, z surf ) where z surf is the position of the surface of the sample [33]. According to Eq. 35.4, the product of J all (x, y, z) and the inverse of J all (x, y, z surf ) is expressed as
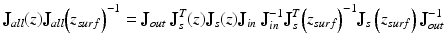
where the variables of x and y are omitted for simplicity. By using the fact that J s (z surf ) is a unit matrix, Eq. 35.6 is simplified to be
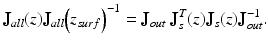
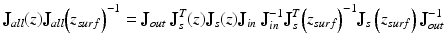
(35.6)
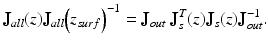
(35.7)
On the other hand, by using the relationship of Eq. 35.5, the same product of J all (z)J all (z surf )−1 is also expressed as
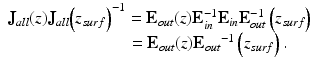
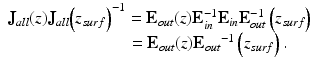
(35.8)
By combining Eqs. 35.7 and 35.8, the key equation of Jones matrix OCT
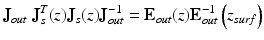
is obtained. The left-hand side is a similar matrix of the round-trip Jones matrix of the sample, while the right-hand side consists of only measurable values.
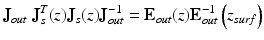
(35.9)
In general, a matrix and its similar matrix possess the same eigenvalues. Therefore, the eigenvalues of the matrix obtained by Eq. 35.9 provide the round-trip phase retardation and the diattenuation of the sample. It is also noteworthy that this equation does not consist of E in . It indicates the selection of two polarization states of the two incident light beams 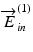 and
and  is arbitrary as far as E in is a non-singular matrix (see also Sect. 35.2.1).
is arbitrary as far as E in is a non-singular matrix (see also Sect. 35.2.1).
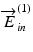 and
and  is arbitrary as far as E in is a non-singular matrix (see also Sect. 35.2.1).
is arbitrary as far as E in is a non-singular matrix (see also Sect. 35.2.1).35.2.3 Phase Retardation, Diattenuation, and Relative Optic-Axis Orientation
After determining the similar matrix of the round-trip Jones matrix by using Eq. 35.9, its eigenvalues and eigenvectors are obtained through one of the general numerical eigenvalue algorithms, for instance, which are described in Ref. 33. Such eigenvalue algorithms [35] are frequently available in standard programming libraries/languages for numerical computation, such as LAPACK (for Fortran 90 and C), MATLAB, and LabVIEW. The eigenvalues can also be obtained by the following equation

where T and D are the trace and the determinant of the similar matrix, respectively.

(35.10)
The phase retardation, diattenuation, and relative optic-axis orientation are then determined by these eigenvalues and eigenvectors as described in the following subsections.
35.2.3.1 Phase Retardation
The phase retardation δ is determined by the phase difference between two eigenvalues as
![$$ \delta \equiv \mathrm{A}\mathrm{r}\mathrm{g}\left[{\lambda}_1/{\lambda}_2\right]= \arctan \left[\frac{\mathrm{Im}\left({\lambda}_1/{\lambda}_2\right)}{\mathrm{Re}\left({\lambda}_1/{\lambda}_2\right)}\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_Equ11.gif)
![$$ \delta \equiv \mathrm{A}\mathrm{r}\mathrm{g}\left[{\lambda}_1/{\lambda}_2\right]= \arctan \left[\frac{\mathrm{Im}\left({\lambda}_1/{\lambda}_2\right)}{\mathrm{Re}\left({\lambda}_1/{\lambda}_2\right)}\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_Equ11.gif)
(35.11)
Although it is omitted for simplicity, δ, λ 1, and λ 2 are the functions of (x, y, z), such that a tomography of double-path phase retardation is obtained. In addition, the phase retardation measured at a particular position in the sample is affected by its anterior tissue. Thus, this phase retardation is a cumulative double-path phase retardation from the surface of the sample to the depth position being measured.
It should be noted that the selection of λ 1 and λ 2 from the two numerically obtained eigenvalues is arbitrary; the phase-retardation value has an ambiguity of π rad. For practical Jones matrix OCT, the phase retardation is aliased into a 0 to π rad range as
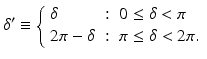
where δ’ is the aliased double-path phase retardation.
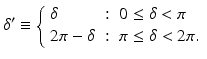
(35.12)
35.2.3.2 Diattenuation
The diattenuation d is defined as the contrast of the amplitudes of the eigenvectors as
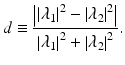
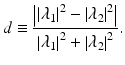
(35.13)
Since λ 1 and λ 2 are the functions of (x, y, z), d is also a function of (x, y, z) and represents the tomography of diattenuation.
35.2.3.3 Relative Optic-Axis Orientation
The relative optic-axis orientation is defined as the direction of an eigenvector, which is a Jones vector of a characteristic polarization state of the similar matrix, on the equatorial plane of the Poincaré sphere. It should be noted that this eigenvector is not an eigenvector of the round-trip Jones matrix of the sample but that of the similar matrix. Hence, the optic-axis orientation obtained by this method is not identical to that of the sample but only a relative axis orientation.
Although this relative axis orientation is not a direct property of the sample, it would provide useful information to the extent that J out is constant. In addition, a calibration technique of Jones matrix OCT that enables the absolute optic-axis orientation has recently been presented [36].
35.2.3.4 Degree of Polarization Uniformity
In addition to the abovementioned fundamental polarization properties, Jones matrix tomography can also be utilized to obtain the secondary polarization property of the sample, the so-called degree of polarization uniformity (DOPU) [37, 38]. DOPU measurement by PS-OCT was independently proposed by Lee et al. [37] and Götzinger et al. [38]. DOPU is known to be associated with melanin concentration in the sample [39] and has been utilized for the segmentation of the retinal pigment epithelium [38].
DOPU is defined by spatially averaged Stokes parameters of the backscattered probe beam as
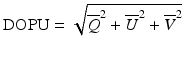
where 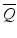 ,
, 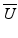 , and
, and 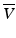 are the normalized Stokes parameters defined as
are the normalized Stokes parameters defined as
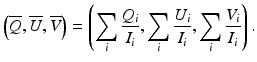
[I i Q i U i V i ] T is a Stokes vector of the ith pixel in a spatial kernel of the averaging. Since OCT is a coherence imaging modality, it is not possible to measure the degree of polarization [30]. However, DOPU is regarded as a spatial analogy of the degree of polarization.
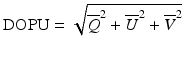
(35.14)
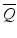 ,
, 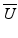 , and
, and 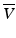 are the normalized Stokes parameters defined as
are the normalized Stokes parameters defined as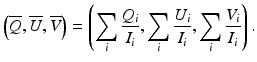
(35.15)
Although DOPU is defined from the Stokes parameters, Jones matrix OCT can also provide DOPU from the Jones matrix by assuming a virtual incident beam and its resulting virtual output Stokes vector. For example, by assuming the incident polarization state of [1 0] T , the virtual Stokes parameters are defined as
![$$ \left[\begin{array}{c}\hfill I\hfill \\ {}\hfill Q\hfill \\ {}\hfill U\hfill \\ {}\hfill V\hfill \end{array}\right]\equiv \left[\begin{array}{c}\hfill {\left|{J}_{11}\right|}^2+{\left|{J}_{12}\right|}^2\hfill \\ {}\hfill {\left|{J}_{11}\right|}^2-{\left|{J}_{12}\right|}^2\hfill \\ {}\hfill {J}_{11}{J}_{12}^{*}+{J}_{11}^{*}{J}_{12}\hfill \\ {}\hfill i\left({J}_{11}{J}_{12}^{*}-{J}_{11}^{*}{J}_{12}\right)\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_Equ16.gif)
where J 11 and J 12 are the upper-left and lower-left entries of the similar matrix J all (z)J all (z surf )−1 = E out (z)E out −1(z surf ).
![$$ \left[\begin{array}{c}\hfill I\hfill \\ {}\hfill Q\hfill \\ {}\hfill U\hfill \\ {}\hfill V\hfill \end{array}\right]\equiv \left[\begin{array}{c}\hfill {\left|{J}_{11}\right|}^2+{\left|{J}_{12}\right|}^2\hfill \\ {}\hfill {\left|{J}_{11}\right|}^2-{\left|{J}_{12}\right|}^2\hfill \\ {}\hfill {J}_{11}{J}_{12}^{*}+{J}_{11}^{*}{J}_{12}\hfill \\ {}\hfill i\left({J}_{11}{J}_{12}^{*}-{J}_{11}^{*}{J}_{12}\right)\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_Equ16.gif)
(35.16)
The DOPU is also directly calculated from E out (z) by substituting J 11 = E out,11 and J 12 = E out,12 into Eq. 35.16, where E out,11 and E out,12 are the upper-left and lower-left entries of the Jones vector matrix E out (z), respectively. Note that, in this case, the assumed virtual incident polarization state is ![$$ {\mathbf{E}}_{out}\left({z}_{surf}\right){\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_IEq30.gif) .
.
![$$ {\mathbf{E}}_{out}\left({z}_{surf}\right){\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_36_Chapter_IEq30.gif) .
.35.3 Implementation Theory
As we discussed in Sect. 35.2, Jones matrix OCT relies on two incident polarization states and Jones vector measurement of the backscattered beam. The former is realized by one of the polarization multiplexing mechanisms, and the latter is typically realized by a polarization-diversity detection scheme. This section is dedicated to providing a brief review of these methods.
35.3.1 Multiplexing of Incident Polarization States
As is evident from Eq. 35.1, Jones matrix OCT relies on two incident polarization states. These two polarization states are multiplexed by several means in Jones matrix OCT measurement including time-division multiplexing [33], polarization modulation along the transversal scan (mainly for spectral domain (SD-)OCT) [40] or along the wavelength scan (only for swept-source (SS-)OCT) [41], frequency shifting [42], and time delay-based multiplexing [43, 44].
35.3.1.1 Time-Division Multiplexing
In the time-division multiplexing scheme, two polarization states of the incident beam are sequentially switched for A-line by A-line [33]. This method is the most straightforward implementation of incident polarization multiplexing.
35.3.1.2 Polarization Modulation Along the Transverse Scan
In this multiplexing scheme, the phase of a polarization component of incident light is modulated by a sinusoidal function along the transversal scanning direction. By this modulation, two incident beams with two polarization states are multiplexed such that one is modulated in phase and the other is not. After OCT detection, these two multiplexed components are demultiplexed by spatial frequency filtering based on a numerical Fourier transform along the transversal direction [40].
The modulation is typically performed by an electro-optic (EO) modulator as shown in Fig. 35.2. The EO modulator is configured to modulate the relative phase of the polarization component of a probe beam that oriented to one of the axes of the modulator (so denoted as EO-modulation axis) in respect to the phase of the OCT reference beam, while the relative phase of the polarization component oriented to the other EO axis (EO-non-modulation axis) is not modulated. The frequency of the modulation is defined in respect to the A-line frequency of the OCT detection so that it is several fractions of the A-line frequency. An example of the modulation frequency was 9.23 kHz, which is one-third of the A-line frequency of 27.7 kHz [40]. Consequently, the modulation frequency of this method is around ten few kHz.
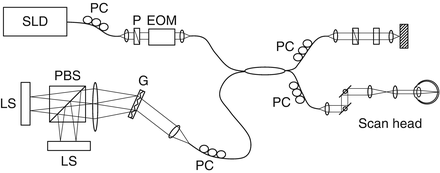

Fig. 35.2
Example of the optical scheme for polarization modulation along the transversal scan. SLD is a superluminescent diode light source, PCs are polarization controllers, LPs are linear polarizers, ND is neutral density filter, and EOM is an electro-optic modulator. This modulation scheme is particularly suitable for the SD-OCT scheme, and this example is equipped with a polarization-diversity spectrometer consisting of a grating (G), a polarization beam splitter (PBS), and two line scan CCD cameras
With the phase modulation depth of 2.405 rad, the theoretical modulation efficiency in the EO-modulation axis, which is the ratio of the total optical power of the modulated beam including those of high-order harmonics over non-modulated optical power in the EO-modulation axis, is 100 %. Under this condition, the polarization states of the non-modulated incident beam, which would be 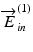 , and the modulated incident beam
, and the modulated incident beam 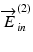 are orthogonal to each other, and the maximum robustness of phase-retardation measurement is obtained [45].
are orthogonal to each other, and the maximum robustness of phase-retardation measurement is obtained [45].
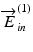 , and the modulated incident beam
, and the modulated incident beam 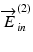 are orthogonal to each other, and the maximum robustness of phase-retardation measurement is obtained [45].
are orthogonal to each other, and the maximum robustness of phase-retardation measurement is obtained [45].Because of several kinds of turbulences, such as temperature drift, and imperfection of the EO modulator, the accurate modulation depth of 2.405 rad is hard to achieve in practice. Under non-ideal modulation conditions, 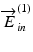 and
and 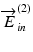 are no longer orthogonal to each other. However, it is noteworthy that the extended principle of Jones matrix OCT also holds its validity for this non-ideal case because it does not rely on the orthogonality of the incident polarization states.
are no longer orthogonal to each other. However, it is noteworthy that the extended principle of Jones matrix OCT also holds its validity for this non-ideal case because it does not rely on the orthogonality of the incident polarization states.
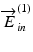 and
and 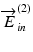 are no longer orthogonal to each other. However, it is noteworthy that the extended principle of Jones matrix OCT also holds its validity for this non-ideal case because it does not rely on the orthogonality of the incident polarization states.
are no longer orthogonal to each other. However, it is noteworthy that the extended principle of Jones matrix OCT also holds its validity for this non-ideal case because it does not rely on the orthogonality of the incident polarization states.35.3.1.3 Polarization Modulation Along the Wavelength Scan
This scheme is a variation of the abovementioned polarization modulation method and is specifically applicable to SS-OCT. The phase modulation is performed by an EO modulator with a similar optical scheme to that in Fig. 35.2 but along the wavelength scan. Similar to the modulation along the transversal scan, the two incident polarization states are demultiplexed by frequency filtering but based on a numerical Fourier transform along the wavelength scan [41].
This scheme requires a typical modulation frequency of one-third or slightly less than half of the sampling frequency of wavelength sampling. A typical modulation frequency is 33.3 MHz [41] or 40 MHz [46] for a sampling frequency of 100 MHz. Therefore, the modulation frequency of this scheme is around a few 10 MHz and is higher than that of modulation along the transversal scan by a magnitude greater than 1,000. This high-frequency operation requires a resonant EO modulator [41] or a wave guide-based miniature EO modulator [7]. These EO modulators could be a potential limitation of the implementation of this method. On the other hand, similar to the transversal modulation scheme, the incident polarization states are not necessarily orthogonal. This fact relaxes the requirement for the implementation.
An advantage of this method over the transversal modulation is that  and
and 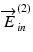 are simultaneously obtained at exactly the same location in the sample. In the transversal modulation scheme, the probe locations on the sample corresponding to the two incident polarizations are slightly displaced to each other because the EO modulator alters the incident polarization state for each A-line. This small displacement results in a structural decorrelation between two OCT signals associated with the two incident polarization states, and it finally degrades the sensitivity of the Jones matrix measurement. This issue raises an additional requirement of the transversal modulation scheme, i.e., the A-lines should be dense enough in space so that the separation between adjacent A-lines is less than a fraction of the transversal optical resolution. The wide-range and high-speed measurements are in contradiction to each other with the transversal modulation scheme.
are simultaneously obtained at exactly the same location in the sample. In the transversal modulation scheme, the probe locations on the sample corresponding to the two incident polarizations are slightly displaced to each other because the EO modulator alters the incident polarization state for each A-line. This small displacement results in a structural decorrelation between two OCT signals associated with the two incident polarization states, and it finally degrades the sensitivity of the Jones matrix measurement. This issue raises an additional requirement of the transversal modulation scheme, i.e., the A-lines should be dense enough in space so that the separation between adjacent A-lines is less than a fraction of the transversal optical resolution. The wide-range and high-speed measurements are in contradiction to each other with the transversal modulation scheme.
 and
and 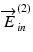 are simultaneously obtained at exactly the same location in the sample. In the transversal modulation scheme, the probe locations on the sample corresponding to the two incident polarizations are slightly displaced to each other because the EO modulator alters the incident polarization state for each A-line. This small displacement results in a structural decorrelation between two OCT signals associated with the two incident polarization states, and it finally degrades the sensitivity of the Jones matrix measurement. This issue raises an additional requirement of the transversal modulation scheme, i.e., the A-lines should be dense enough in space so that the separation between adjacent A-lines is less than a fraction of the transversal optical resolution. The wide-range and high-speed measurements are in contradiction to each other with the transversal modulation scheme.
are simultaneously obtained at exactly the same location in the sample. In the transversal modulation scheme, the probe locations on the sample corresponding to the two incident polarizations are slightly displaced to each other because the EO modulator alters the incident polarization state for each A-line. This small displacement results in a structural decorrelation between two OCT signals associated with the two incident polarization states, and it finally degrades the sensitivity of the Jones matrix measurement. This issue raises an additional requirement of the transversal modulation scheme, i.e., the A-lines should be dense enough in space so that the separation between adjacent A-lines is less than a fraction of the transversal optical resolution. The wide-range and high-speed measurements are in contradiction to each other with the transversal modulation scheme.On the other hand, in the wavelength scan-oriented modulation scheme, the OCT signals associated with two incident polarization states are obtained at exactly the same time and location. Hence, the structural decorrelation does not occur. This property makes the wavelength-oriented modulation scheme suitable for high-speed wide-range measurements.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


