. A linear mapping is assumed which associates the two functions:
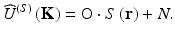
(4.1)
(Usually, there will be some noise N too.) O is a linear operator describing the scattering process. Here, the experimental procedure involves sampling and in particular severe bandwidth limitations (Fig. 4.2); hence, an inversion of Eq. 4.1 is not a well-posed problem. A similar problem occurs in optical imaging by lenses; here aperture limits of the spatial frequency components in image are countersteered by deconvolution techniques. Such ill-posed problems are usually treated by regularization. The regularization method is based on approximate solutions depending on a regularization parameter that tends to zero, when the approximate solution converges to the exact solution [15].
4.1 Optical Diffraction Tomography-Based Inverse Scattering
4.1.1 Basic Theorem of Diffraction Tomography
Optical diffraction tomography (ODT) is based on IS. The scattering operator O essentially is a three-dimensional (3D) Fourier transform (FT). Tikhonov regularization [16] can be used to improve both, signal-to-noise ratio and image qualities. In formulating the basic theorem of diffraction tomography [5], E. Wolf considers direct scattering on a nonmagnetic sample with an isotropic dielectric constant varying weakly over distances of the order of a wavelength. That sample is assumed illuminated by a plane wave or positioned at the beam waist of a monochromatic Gaussian beam with amplitude
![$$ {U}^{(i)}\left(\mathbf{r}\right)={A}^{(i)}\left(\mathbf{r}\right) \exp \left[-i\omega t\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ2.gif)
![$$ {U}^{(i)}\left(\mathbf{r}\right)={A}^{(i)}\left(\mathbf{r}\right) \exp \left[-i\omega t\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ2.gif)
(4.2)
Wolf’s solution is based on the first-order Born approximation as an approximate solution for weak scatterers. Weyl’s expansion of the 3D free-space Green function of the wave equation lets him represent the scattered field as an angular spectrum of plane waves. In a first step Wolf thus obtains an expression for the angular spectrum of homogeneous waves of the scattered field 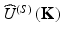 in terms of the 3D Fourier inverse of the sample scattering potential F(r). As a second step Wolf determines the homogeneous part of the angular spectrum of scattered waves by a two-dimensional (2D) FT
in terms of the 3D Fourier inverse of the sample scattering potential F(r). As a second step Wolf determines the homogeneous part of the angular spectrum of scattered waves by a two-dimensional (2D) FT  of the scattered field U (s)(r) in detection planes in front and behind the scattering object and adds a phase factor corresponding to the distance between sample and detection plane [1].
of the scattered field U (s)(r) in detection planes in front and behind the scattering object and adds a phase factor corresponding to the distance between sample and detection plane [1].
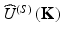 in terms of the 3D Fourier inverse of the sample scattering potential F(r). As a second step Wolf determines the homogeneous part of the angular spectrum of scattered waves by a two-dimensional (2D) FT
in terms of the 3D Fourier inverse of the sample scattering potential F(r). As a second step Wolf determines the homogeneous part of the angular spectrum of scattered waves by a two-dimensional (2D) FT  of the scattered field U (s)(r) in detection planes in front and behind the scattering object and adds a phase factor corresponding to the distance between sample and detection plane [1].
of the scattered field U (s)(r) in detection planes in front and behind the scattering object and adds a phase factor corresponding to the distance between sample and detection plane [1].Alternative approaches to determine the spatial distribution of magnitude and phase of wave fields under far-field and near-field conditions have been given by Schmidt-Weinmar [17, 18]. The first applications of the ODT theorem were demonstrated by Carter [2], who considered the special case of a rectangular scatterer and compared the computed projection of the scattering potential along a planar section through the object with experimental measurements and furthermore, by Carter and Ho [19], who considered a semitransparent bar with nonuniform index of refraction and stated agreement between the computed 1D (one-dimensional) scattering potential along a line through the object with known object parameters within errors of a few percent.
Another frequently used solution of the inverse scattering problem is the Rytov expansion; it models the phase of the scattered field as exponentially dependent on the scattering potential [5]. Whereas the first-order Born approximation is accurate when the product of the index contrast and object size is less than one-quarter wavelength, the Rytov approximation is accurate when the square of the phase gradient is much less than the index contrast divided by the wavelength squared [20]. If continuities of the sample parameters are located on smooth surfaces, the Kirchhoff approximation is a preferred solution [21].
In 2002 Lauer [22] has presented a new approach to optical diffraction tomography. In this technique the sample is successively illuminated by a series of plane waves having different directions; the sample structure is then reconstructed from these recorded waves.
At present, the basic theorem of diffraction tomography forms the physical basis of many PCI and OCT techniques as well as of the recently put forward synthetic-aperture technique [23].
4.1.2 Far-Field Approximation
Far-field diffraction or Fraunhofer conditions are defined with respect to sample size and detection plane to sample distance. In this case the scattered field is observed at a distance d ≫ a 2/λ or at a Fresnel number 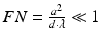 ; a is a length of the order of the size of the sample. Under these conditions the first-order Born approximation for an incident wave U (i)(r′) = A (i) ⋅ exp[i ⋅ k (i) ⋅ r′] yields a spherical wave for the scattered field at the detection plane with a complex amplitude determined by the FT of the sample scattering potential F(r) [3]:
; a is a length of the order of the size of the sample. Under these conditions the first-order Born approximation for an incident wave U (i)(r′) = A (i) ⋅ exp[i ⋅ k (i) ⋅ r′] yields a spherical wave for the scattered field at the detection plane with a complex amplitude determined by the FT of the sample scattering potential F(r) [3]:
![$$ {U}^{(S)}\left(\mathbf{r},k\right)=-\frac{1}{4\pi }{\displaystyle \underset{Vol}{\int }{U}^{(i)}\cdot \left({\mathbf{r}}^{\prime}\right)\cdot F\left({\mathbf{r}}^{\prime}\right)}\cdot \frac{ \exp \left[i\cdot k\cdot \left|\mathbf{r}-{\mathbf{r}}^{\prime}\right|\right]}{\left|\mathbf{r}-{\mathbf{r}}^{\prime}\right|}\cdot {d}^3{\mathbf{r}}^{\prime }; $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ3.gif)
the fraction in this equation is the Green function of the wave equation. With direct space origin in or close to the sample, we can use the approximation k ⋅ |r − r′| ≈ k (S) ⋅ (r − r′), k = 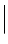 k (i)
k (i) 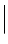 =
= 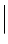 k (S)
k (S) 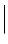 = 2π/λ. r is the far-field position vector. (We have omitted the self-evident time-dependence exp[−i ⋅ ω ⋅ t].)
= 2π/λ. r is the far-field position vector. (We have omitted the self-evident time-dependence exp[−i ⋅ ω ⋅ t].)
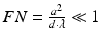 ; a is a length of the order of the size of the sample. Under these conditions the first-order Born approximation for an incident wave U (i)(r′) = A (i) ⋅ exp[i ⋅ k (i) ⋅ r′] yields a spherical wave for the scattered field at the detection plane with a complex amplitude determined by the FT of the sample scattering potential F(r) [3]:
; a is a length of the order of the size of the sample. Under these conditions the first-order Born approximation for an incident wave U (i)(r′) = A (i) ⋅ exp[i ⋅ k (i) ⋅ r′] yields a spherical wave for the scattered field at the detection plane with a complex amplitude determined by the FT of the sample scattering potential F(r) [3]:![$$ {U}^{(S)}\left(\mathbf{r},k\right)=-\frac{1}{4\pi }{\displaystyle \underset{Vol}{\int }{U}^{(i)}\cdot \left({\mathbf{r}}^{\prime}\right)\cdot F\left({\mathbf{r}}^{\prime}\right)}\cdot \frac{ \exp \left[i\cdot k\cdot \left|\mathbf{r}-{\mathbf{r}}^{\prime}\right|\right]}{\left|\mathbf{r}-{\mathbf{r}}^{\prime}\right|}\cdot {d}^3{\mathbf{r}}^{\prime }; $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ3.gif)
(4.3)
 k (i)
k (i)  =
=  k (S)
k (S) 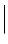 = 2π/λ. r is the far-field position vector. (We have omitted the self-evident time-dependence exp[−i ⋅ ω ⋅ t].)
= 2π/λ. r is the far-field position vector. (We have omitted the self-evident time-dependence exp[−i ⋅ ω ⋅ t].)Equation 4.3 can now be written as
![$$ \begin{array}{l}{\widehat{U}}^{(S)}\left(\mathbf{K}\right)=-\frac{1}{4\cdot \pi }{\displaystyle \underset{Vol}{\int }F\left({\mathbf{r}}^{\prime}\right)\cdot {A}^{(i)}\left({\mathbf{r}}^{\prime}\right)\cdot \frac{ \exp \left[i\cdot {\mathbf{k}}^{\left(\mathbf{S}\right)}\left(\mathbf{r}\right)\right]}{\left|\mathbf{r}-{\mathbf{r}}^{\prime}\right|}\cdot \exp \left[-i\cdot \left({\mathbf{r}}^{\prime}\cdot \mathbf{K}\right)\right]}\cdot {d}^3{\mathbf{r}}^{\prime}\\ {}\kern3.4em =-\frac{ \exp \left(i\cdot k\cdot d\right)}{4\cdot \pi \cdot d}{\displaystyle \underset{Vol}{\int }{A}^{(i)}\left({\mathbf{r}}^{\prime}\right)\cdot F\left({\mathbf{r}}^{\prime}\right)\cdot \exp \left(-i\cdot \mathbf{K}\cdot {\mathbf{r}}^{\prime}\right)\cdot {d}^3{\mathbf{r}}^{\prime }},\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ4.gif)
since, in the far-field, both the scattering vector K = k (S) − k (i) and the vector of the scattered wave k (S) can be used to define the position r of field detection. k (i) is the wave vector of the incident wave ( k (i)
k (i) 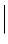 =
=  k (S)
k (S) 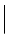 = k = 2π/λ). d is the distance between direct space origin at or near the sample and the field position. F(r) is the sample scattering potential – see Eq. 4.7 below. Hence, the scattered wave comprises a spectrum of spherical waves with radius of curvature d and a complex amplitude equal to the inverse Fourier transform of the sample source strength
= k = 2π/λ). d is the distance between direct space origin at or near the sample and the field position. F(r) is the sample scattering potential – see Eq. 4.7 below. Hence, the scattered wave comprises a spectrum of spherical waves with radius of curvature d and a complex amplitude equal to the inverse Fourier transform of the sample source strength
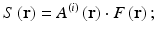
![$$ \begin{array}{l}{\widehat{U}}^{(S)}\left(\mathbf{K}\right)=-\frac{1}{4\cdot \pi }{\displaystyle \underset{Vol}{\int }F\left({\mathbf{r}}^{\prime}\right)\cdot {A}^{(i)}\left({\mathbf{r}}^{\prime}\right)\cdot \frac{ \exp \left[i\cdot {\mathbf{k}}^{\left(\mathbf{S}\right)}\left(\mathbf{r}\right)\right]}{\left|\mathbf{r}-{\mathbf{r}}^{\prime}\right|}\cdot \exp \left[-i\cdot \left({\mathbf{r}}^{\prime}\cdot \mathbf{K}\right)\right]}\cdot {d}^3{\mathbf{r}}^{\prime}\\ {}\kern3.4em =-\frac{ \exp \left(i\cdot k\cdot d\right)}{4\cdot \pi \cdot d}{\displaystyle \underset{Vol}{\int }{A}^{(i)}\left({\mathbf{r}}^{\prime}\right)\cdot F\left({\mathbf{r}}^{\prime}\right)\cdot \exp \left(-i\cdot \mathbf{K}\cdot {\mathbf{r}}^{\prime}\right)\cdot {d}^3{\mathbf{r}}^{\prime }},\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ4.gif)
(4.4)
 k (i)
k (i) 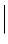 =
=  k (S)
k (S) 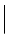 = k = 2π/λ). d is the distance between direct space origin at or near the sample and the field position. F(r) is the sample scattering potential – see Eq. 4.7 below. Hence, the scattered wave comprises a spectrum of spherical waves with radius of curvature d and a complex amplitude equal to the inverse Fourier transform of the sample source strength
= k = 2π/λ). d is the distance between direct space origin at or near the sample and the field position. F(r) is the sample scattering potential – see Eq. 4.7 below. Hence, the scattered wave comprises a spectrum of spherical waves with radius of curvature d and a complex amplitude equal to the inverse Fourier transform of the sample source strength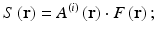
(4.5)
This corresponds to the first step of Wolf’s solution. In the far-field approximation Wolf’s second step occurs by light propagation to the detector matrix. Using that facilitation Fercher et al. [3] were the first to demonstrate a full 3D reconstruction of a 3D object based on ODT. Computer simulations based on Mie scattering by coated spheres and reconstructions based on experimentally obtained scattered field data were presented. However, these early (1979) investigations suffered from limitations of light source and computer technology at that time.
For simplification of the subsequent discussion of the properties of diffraction tomography, we shall use the far-field approximation of the basic ODT theorem. This approximation in particular describes digital microscopic imaging but is easily extended to large samples as well; see Sect. 4.2.1.6 below. In this approximation the complex amplitude of the scattered wave 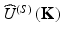 represents the Fourier components of the sample source strength accessible by scattered field measurements:
represents the Fourier components of the sample source strength accessible by scattered field measurements:
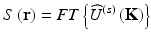
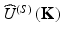 represents the Fourier components of the sample source strength accessible by scattered field measurements:
represents the Fourier components of the sample source strength accessible by scattered field measurements: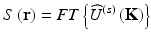
(4.6)
As depicted in Fig. 4.1 forward and backward scattering provide access to quite different Fourier components of the sample structure.
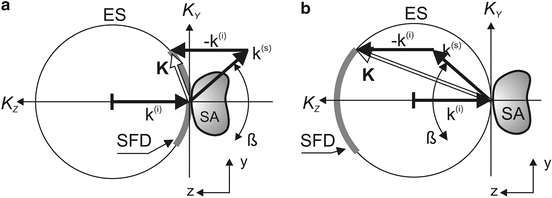

Fig. 4.1
Forward and backward far-field scattering: (a) scattered field data (SFD) in forward scattering are located around K Z ∼ 0; (b) scattered field data in backscattering are located around K Z ∼ −2k. ES Ewald sphere, SA sample, SFD accessible scattered field data. ß is the aperture angle
4.1.3 Basic Properties of Optical Diffraction Tomography-Based Inverse Scattering
1.
Sample structure, represented as source strength S(r) = A (i)(r) ⋅ F(r), is obtained from a Fourier transform of the complex amplitude of the far-field scattered sample wave.
2.
Source strength structure is mainly determined by the scattering potential F(r) (also called “scattering contrast,” or “sample susceptibility”) of the sample:
![$$ F\left(\mathbf{r}\right)={k}^2\cdot \left[{m}^2\left(\mathbf{r}\right)-1\right], $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ7.gif)
![$$ F\left(\mathbf{r}\right)={k}^2\cdot \left[{m}^2\left(\mathbf{r}\right)-1\right], $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ7.gif)
(4.7)
m(r) = n(r) ⋅ [1 + i ⋅ κ ⋅ (r)] is the complex refractive index distribution of the sample structure, with n(r) = phase refractive index and K(r) = attenuation index. (A more general expression of the scattering potential is achieved if the changes in refractive index are measured relative to the background refractive index [24].)
4.
The lateral extent of the transfer function for both, forward and backscattering, is the same. In both cases lateral resolution is the same (depending on aperture angle ß).
4.
Forward scattering, even at moderately large aperture angles, provides access only to Fourier data near the K x −K y plane (K z ∼ 0). Hence, with respect to depth structure, forward scattering techniques act as low-pass filter. The image obtained in standard optical imaging, for example, by lenses, is a projection of the sample structure in z-direction [25]. High depth resolution in standard imaging demands for rather large aperture angles, as used, e.g., in high-resolution microscopy.
6.
Standard OCT techniques use low numerical apertures (NAs) of the probing sample beam optics. Hence, the major contribution to the detected light comes from backscattering. For further details see Sheppard et al. [24].
7.
8.
Resolution is determined by the Fourier uncertainty relation:
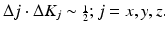
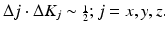
(4.8)
Even at moderate aperture angles ß (Fig. 4.1), relatively large ranges of transversal Fourier components are accessible in forward and backward scattering, and thus relatively high transversal resolution Δx and Δy can be obtained. In contrast to standard optical imaging, high depth resolution in PCI and OCT A-scan signals is provided by a broad wavelength spectrum Δλ. Here depth resolution is usually defined by the coherence length  (Gaussian spectrum assumed,
(Gaussian spectrum assumed,  is the mean wavelength).
is the mean wavelength).
 (Gaussian spectrum assumed,
(Gaussian spectrum assumed,  is the mean wavelength).
is the mean wavelength).9.
Backscattering detector signal strength is, besides its dependence on the detector aperture, proportional to K 2 and, therefore, proportional to the second-order derivative F (2)(z) of the scattering potential [26]:
![$$ {F}^{(2)}(z)=-2\cdot {k}_0^2\cdot \left[{n}^{(1)}{(z)}^2+n(z)\cdot {n}^{(2)}(z)\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ9.gif)
![$$ {F}^{(2)}(z)=-2\cdot {k}_0^2\cdot \left[{n}^{(1)}{(z)}^2+n(z)\cdot {n}^{(2)}(z)\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ9.gif)
(4.9)
LCI and OCT signals, therefore, increase with increasing steepness and variability of the sample refractive index. (The same prediction has recently been obtained from another scattering model, based on the Kirchhoff approximation [24].)
10.
Finally, the photoelectric OCT signal is proportional to the interferogram intensity at the photodetector and its quantum efficiency.
In this chapter, inversion of backscattered light in the far-field approximation provides the key to Fourier domain PCI and OCT. However, inversion problems also occur in forward scattering, for example, in near-field optics; in diverse areas of biological and industrial applications, such as the imaging of biological samples; in the inspection and manipulation of nano-electronic components in semiconductor technology; and in the inspection and activation of nano-optical devices.
4.2 Inverse Scattering-Based OCT Techniques
4.2.1 Far-Field Diffraction Techniques
In near-field Fresnel diffraction tomography, the operator O comprises two consecutive FTs [1]. Far-field diffraction tomography, on the other hand, is based on one FT only. Hence, we shall concentrate on far-field diffraction tomography and may expect most results to be applicable in near-field Fresnel diffraction tomography as well.
Based on optical diffraction tomography, a hierarchy of tomographic techniques can be formulated [28, 29], each based on a wavelength spectrum from λ1 to λ2 – starting from 3D imaging as indicated in Fig. 4.2 down to the point detector that measures scattering strength of the complete illuminated volume of a sample.
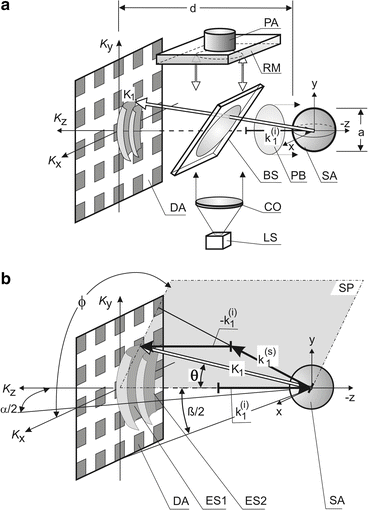

Fig. 4.2
3D far-field DOT. (a) basic optical scheme for inverse scattering-based OCT (and PCI). The illuminating beam vector is assumed antiparallel to the K z -axis of the 2D detector-matrix DA. BS beam splitter, CO collimator, LS tunable or frequency-swept light source, PA piezo actuator for phase-shifting technique, PB probe beam cross section (sample illumination), RM reference mirror, SA sample (homogeneous sphere assumed); (b) K-space geometry of backscattering. Note: here, and in the subsequent figures, the K z = 0 position is at the origin of the x,y,z-system. ESi scattered field data Ewald spheres of wavelength λ i , SP scattering plane. K 1 = scattering vector of wavelength λ 1; k 1(i) = wave vector of illuminating wave of wavelength λ 1; k 1(s) = wave vector of scattered wave of wavelength λ i . Fourier data points of wavelength λ n are in a rectangular window ESn on the surface of the corresponding Ewald spheres. a is the sample size, d is the distance sample/image sensor, ß is the aperture angle, ϕ is the scattering azimuth, θ is the scattering angle
Note: In the subsequent figures standard illumination and reference beam optics as indicated in Fig. 4.2a are omitted.
4.2.1.1 Inverse Scattering 3D Imaging
The optical scheme depicted in Fig. 4.2a is a basic arrangement for 3D ODT giving access to the full 3D sample structure. Basically, in each detector pixel amplitude and phase of the interferogram, formed by the scattered sample wave and the reference wave, have to be measured for the wavelength range λ 1 → λ 2. In the first approach monochromatic light had been used [3]. However, a 3D sample requires the recording of a 3D scattering data set. This can be achieved by illuminating the sample in more than one direction and/or by more than one wavelength [30]. Figure 4.2 depicts the situation when light of a wavelength range λ 1 ≤ λ ≤ λ 2, for example, from a swept source (LS), is used. Here, scattered field data between Ewald sphere windows ES1 and ES2 can be recorded.
Basically, spectral amplitude and spectral phase have to be determined at each detector pixel. Spectral amplitude can easily be obtained from the pixel signal magnitude. There are several approaches to retrieve spectral phase data. For example, the phase-shifting technique enables registering the phase of the scattered field at each detector pixel. In phase-shifting interferometry [31–33], the relative phase of the reference beam is shifted by discrete steps. From the interferometic intensity variation generated by these phase shifts, the phase of the scattered object wave is obtained. Hlubina et al. record two spectral interferograms to obtain the spectral interference signal and retrieve from it the spectral phase [34]. Also, a fast Gabor wavelet transform for high-precision phase retrieval in spectral interferometry that is significantly insensitive toward experimental noise has been described [35]. Using a swept source requires sampling the 2D interferogram intensity formed by the scattered sample wave and the reference wave at each pixel while the frequency of the source is scanned.
These methods are somewhat hindered by the fact that interference spectrum data recorded by single photodetector elements have to be rescaled from wavelength to frequency; furthermore, wavelength-dependent scattering vector space coordinates have to be scaled for wavelength, scattering azimuth, and scattering angle. Such a data set, however, enables a 3D reconstruction of the sample structure, also providing the basis for 2D tomograms.
In contrast, today, standard 3D OCT-based instruments typically use two-axis galvano mirrors for transverse 2D sample scanning by an A-scan probing beam. A-scan information is acquired by spectral interferometry (SI) by either using a broad-bandwidth light source and a spectrometer, spectral domain (SD)-PCI, or sweeping a narrow-bandwidth source through a broad range of frequencies, swept source (SS)-PCI. In both cases A-scan depth information is obtained by a Fourier transform of the detected spectra [36]. A comparison of a recently available commercial 3D OCT system operating at 800 nm with three laboratory systems operating with higher A-scans/s and one different wavelength can be found by Povazay et al. [37].
4.2.1.2 Inverse Scattering Sample Slice Generation
Direct access to tomographic sample sections is provided by projected scattering data. This follows from the Fourier projection/slice theorem [38]. Section position and orientation can be chosen within wide limits. For example, a slice S(x 0, y, z) of the sample source strength in the y–z plane at x-coordinate x 0 is obtained from a projection of the scattering data including a phase factor:
![$$ S\left({x}_0,y,z\right)={\displaystyle \iint \left\{\left[{\displaystyle \int {\widehat{U}}^{(s)}\left(\mathbf{K}\right)\cdot \exp \left(i\cdot {x}_0\cdot {K}_x\right)\cdot d{K}_x}\right]\cdot \exp \left[i\cdot \left(y\cdot {K}_y+z\cdot {K}_z\right)\right]\right\}}\cdot dKy\cdot dKz. $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ10.gif)
![$$ S\left({x}_0,y,z\right)={\displaystyle \iint \left\{\left[{\displaystyle \int {\widehat{U}}^{(s)}\left(\mathbf{K}\right)\cdot \exp \left(i\cdot {x}_0\cdot {K}_x\right)\cdot d{K}_x}\right]\cdot \exp \left[i\cdot \left(y\cdot {K}_y+z\cdot {K}_z\right)\right]\right\}}\cdot dKy\cdot dKz. $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ10.gif)
(4.10)
(In case of K x − K y − K z − factorizable spectra, a sequence of 1D FTs could be used.)
A slice at x = 0 is simply obtained as a 2D FT of the complex scattering data 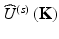 projected in K x -direction in the detection plane
projected in K x -direction in the detection plane
![$$ S\left(0,y,z\right)={\displaystyle \iint \left\{\left[{\displaystyle \int {\widehat{U}}^{(s)}\left(\mathbf{K}\right)\cdot d{K}_x}\right]\cdot \exp \left[i\cdot \left(y\cdot {K}_y+z\cdot {K}_z\right)\right]\right\}}\cdot dKy\cdot dKz. $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ11.gif)
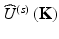 projected in K x -direction in the detection plane
projected in K x -direction in the detection plane![$$ S\left(0,y,z\right)={\displaystyle \iint \left\{\left[{\displaystyle \int {\widehat{U}}^{(s)}\left(\mathbf{K}\right)\cdot d{K}_x}\right]\cdot \exp \left[i\cdot \left(y\cdot {K}_y+z\cdot {K}_z\right)\right]\right\}}\cdot dKy\cdot dKz. $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ11.gif)
(4.11)
Such a projection performance in the detection plane can be achieved by binning sensor pixels of the detector matrix to form corresponding super-pixels in various azimuthal directions. Using programmable detector arrays very flexible OCT sample data acquisition systems can thus be implemented: Besides full 3D imaging, sample slices and sample projections in various orientations could be quickly achieved with such a system.
Projection performance in the detection plane can also be achieved by a linear detector array with reasonable large detector height:
Sample slice generation is analogous to parallel 2D FD-OCT: Grajciar et al. [39], for example, used a cylindrical lens to produce a sheet-of-light illumination on the sample in a study on a fully parallel FD-OCT system that allowed real time imaging of human eye structures. An alternative has been proposed by Zuluaga et al. [40]. These authors used a spatially resolved spectral interferometer. Here the depth in the sample is encoded as wavelength-dependent spatial frequency in the spectrogram whereas transverse information is imaged directly.
4.2.1.3 Inverse Scattering Sample Projection
Consider a 2D slice through the scattered field in the K y −K z plane at K x = 0:


![$$ \begin{array}{l}{\widehat{U}}^{(S)}\left(0,{K}_y,{K}_z\right)={\displaystyle \int \kern-0.35em \iint S\left(x,y,z\right)}\cdot \exp \left[-i\cdot \left(x\cdot {K}_x+y\cdot {K}_y+z\cdot {K}_z\right)\right]\cdot dx\cdot dy\cdot dz\left|{}_{K_x=0}\right.\\ {}={\displaystyle \iint \left\{\left[{\displaystyle \int S\left(x,y,z\right)\cdot dx}\right]\cdot \exp \left[-i\cdot \left(y\cdot {K}_y+z\cdot {K}_z\right)\right]\right\}}\cdot dy\cdot dz\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_5_Chapter_Equ12.gif)


