(30.1)
where
 is the speckle field amplitude that varies spatially and
is the speckle field amplitude that varies spatially and  is the speckle phase that also varies spatially. The optic axis of the speckle field is defined by the direction of the scattered k-vector
is the speckle phase that also varies spatially. The optic axis of the speckle field is defined by the direction of the scattered k-vector 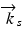 , although this vector also varies spatially. The reference field amplitude is E 0 and the k-vector of the reference is k 0. The coherent speckle hologram intensity is
, although this vector also varies spatially. The reference field amplitude is E 0 and the k-vector of the reference is k 0. The coherent speckle hologram intensity is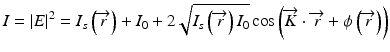
(30.2)
 and the position vector
and the position vector  is in the hologram plane. The first term is the speckle intensity and the second term is the reference intensity. The third term is the coherent interference between the speckle and the reference fields, i. e., the hologram with interference fringes of fringe spacing Λ with
is in the hologram plane. The first term is the speckle intensity and the second term is the reference intensity. The third term is the coherent interference between the speckle and the reference fields, i. e., the hologram with interference fringes of fringe spacing Λ with 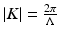 . The hologram amplitude is modulated by the speckle intensity into regions of randomly distributed bright speckles, and the phase of each speckle is independent of each other. However, for off-axis hologram recording, the fringe orientation and spacing Λ are the same for every speckle. This is the spatial heterodyne term that allows coherent detection of depth-resolved scattered light.
. The hologram amplitude is modulated by the speckle intensity into regions of randomly distributed bright speckles, and the phase of each speckle is independent of each other. However, for off-axis hologram recording, the fringe orientation and spacing Λ are the same for every speckle. This is the spatial heterodyne term that allows coherent detection of depth-resolved scattered light.30.3.2 Image-Domain Versus Spatial Fourier-Domain OCI
Holographic OCI was initially performed using image-domain OCI, in which a photorefractive film was located at or near the image plane of the imaging optics. However, dust and other imperfections on the device can produce highly localized scatter in the reconstructed images [25]. These background problems were almost eliminated by conversion of image-domain OCI to Fourier-domain OCI, in which the holographic film is located at the Fourier plane [27]. The key to this conversion is the recognition that diffuse targets such as tissue produce relatively uniform intensity distributions at the Fourier plane (unlike specular test charts that are commonly used for system alignment characterization) permitting uniform hologram recording in the photorefractive film.
The optical configurations for photorefactive holography are shown in Fig. 30.1 for both image-domain and Fourier-domain holography. In Fourier-domain photorefractive OCI, the background scattered from a defect on the holographic film is uniformly distributed at the CCD plane, while it forms a replica of the defect (strong background) in image-domain OCI. In Fourier-domain OCI, in addition to the removal of strong spot background, the total background in the images is reduced and hence the dynamic range is extended. The amount of scattered light that is collected depends on the square of the numerical aperture, where the numerical aperture is proportional to the diameter, D, of the imaging lens in image-domain OCI but size, L, of the imaging CCD chip in Fourier-domain OCI. The ratio of the total background collected in images in image-domain OCI to those for Fourier-domain OCI is (D/L)2. Therefore, Fourier-domain holography enables OCI to become background free in practice, and the signal-to-background ratio in Fourier-domain OCI improved by over 30 dB relative to image-domain OCI and hence allowed the imaging of weaker or thicker objects.


Fig. 30.1
Image-domain holography (IDH) vs. Fourier-domain holography (IDH). Image-domain holography places the holographic film at or near the image plane, while Fourier-domain holography places the holographic film at or near the Fourier plane (Note: FDH is based on spatial Fourier techniques and is not to be confused with spectral techniques)
The full optical system for both photorefractive holography and digital holography is shown in Fig. 30.2. The low-coherence light source is either a mode-locked titanium-sapphire laser (nominal 100 fsec) or a superluminescent diode operating near 840 nm. This is passed through a half-wave plate and a polarizing beam splitter (PBS) to create the signal and reference arms of the Mach-Zehnder interferometer. The intensity ratio of the signal to reference arms is typically 10:1. The signal beam passes through a beam expander and illuminates the biological sample through a second polarizing beam splitter and quarter-wave plate. The returned signal is relayed to an image plane and is then Fourier transformed by lens L4 to the holographic plane. When a PRQW device is at the hologram plane, a physical hologram is recorded and the reconstruction is achieved through diffraction of the reference beam and Fourier transformation by lens L6 to the image plane of a digital camera. Alternatively, the digital camera can be placed at the hologram plane and reconstructed numerically.
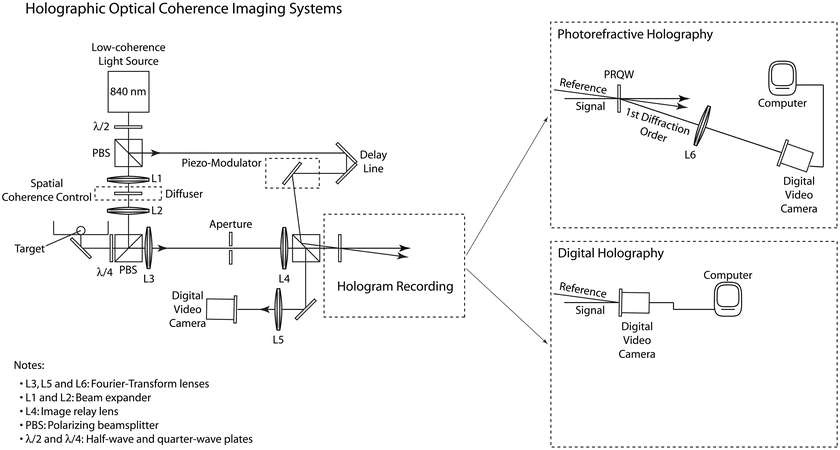

Fig. 30.2
Experimental schematic of the Fourier-domain holography system for photorefractive holography and digital holography. The holographic plane is at the Fourier plane of lens L4. The photorefractive quantum well (PRQW) records a physical hologram that is reconstructed by diffraction to a camera. Alternatively, a CCD chip records a digital hologram that is reconstructed by a FFT algorithm
A specialized capability for photorefractive holography using photorefractive quantum well (PRQW) devices is in speckle reduction. This is achieved by controlling the spatial coherence using a diffuser plate in the beam expander of Fig. 30.2. The diffuser and the steering mirror are vibrated by a piezo-stack at a frequency near 100 Hz. The high-speed photorefractive device tracks the moving hologram fringes in real time, maintaining the diffraction that is the basis of the coherence gating, while the vibrating mirror and vibrating diffuser reduce speckle effects by time-averaging the holographic readout on the camera. These eliminate stray speckle and reduce channel cross talk [53]. Digital holography, on the other hand, cannot use these vibrating mirror or diffuser techniques because the fringes would wash out during the fringe motion. Therefore, photorefractive optical coherence imaging has the advantage of imaging internal structure over digital holographic optical coherence imaging. Digital holography, on the other hand, has an advantage for dynamic speckle studies. Therefore, these two approaches to optical coherence imaging trade off between imaging structure and imaging dynamics.
30.3.3 Photorefractive Holography
Holographic OCI was initially developed using bulk photorefractive crystals and volume holograms [8], which were replaced with photorefractive semiconductor quantum well (PRQW) devices [16] because of their high sensitivity [2, 54]. These devices use molecular beam semiconductor growth processes to produce semiconductor structures that have enhanced optical properties based on quantum localization of electrons in very thin layers (7.5 nm). The enhanced optical properties make these devices sensitive dynamic holographic materials, with interferometric and imaging applications in laser-based ultrasound detection, femtosecond pulse processing, and interferometric bioassays, among others [16, 55–58].
Holographic OCI with PRQW devices uses the same short-coherence light sources as conventional OCT, including either pulsed laser sources or superluminescent diodes. For the PRQW devices, the probe wavelength of the source is at the absorption-edge wavelength of the semiconductor, which is typically λ ≈ 840 nm.
The key performance parameters of the photorefractive quantum wells that are relevant for the OCI application are the minimum writing intensity, the fringe-spacing dependence, and the spectral bandwidth of the quantum well diffraction spectrum. The PRQW devices record fully developed holograms using intensities of only 10–20 μW/cm2. The intensity dependence of wave mixing in a PRQW device is shown in Fig. 30.3a. The data are from two-wave mixing [15], showing fully developed gratings above 20 μW/cm2. The fringe-spacing dependence is shown in Fig. 30.3b. The diffraction efficiency from four-wave mixing increases rapidly above a 5 μm fringe spacing. In speckle holography, a minimum of three fringes are needed per speckle to ensure a well-defined spatial carrier frequency. The 5 μm cutoff places a minimum speckle diameter at around 15 μm. Although speckle size is related to the lateral spatial resolution of the imaging optics, they are not identical, and in the case of Fourier-domain holography, they have an inverse relationship. The bandwidth of the diffraction spectrum is set by the inhomogeneous width of the quantum-confined excitons which is approximately 5 nm. Broader widths are possible through bandgap engineering, but Coulomb correlation effects prevent significantly broader bandwidths to be attained [59, 60].
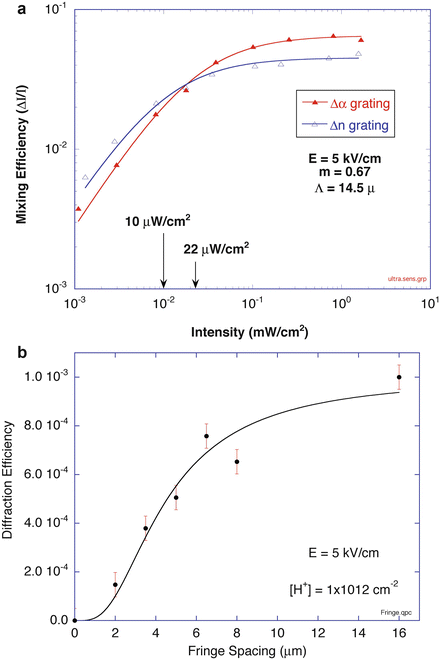

Fig. 30.3
Demonstration of the sensitivity of the holographic film in (a) shows a fully saturated holographic grating for an intensity of only 10–20 μW/cm2. The fringe-spacing dependence in (b) shows a cutoff of 5 μm
30.3.4 Digital Holography
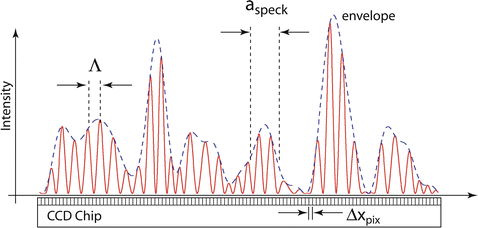
The discreteness of the pixels of a CCD or CMOS array sets limits on the resolution of off-axis digital holography. The interference fringes need to be well sampled by the discrete pixels, as shown in Fig. 30.4. Full resolution is predicted using Nyquist sampling theory, with two pixels per fringe spacing Λ and two fringes per speckle. However, a general rule of thumb for practical implementation is three pixels per fringe and three fringes per speckle. In other words, at the sensor plane, the condition
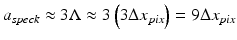
is nominal. These parameters are evaluated on the Fourier plane for Fourier-domain holography. The condition of the speckle size at the camera gives the magnification by lens L4 in Fig. 30.2 to be

where f Obj is the focal length of the objective lens and D tum is the diameter of the tumor. The maximum angle that can be detected is set by the size of the CCD chip, placing a condition on the diameter of the camera detector area and the marginal aperture of the objective lens, through D cam = MD lens , giving another requirement for the magnification
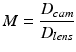
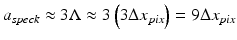
(30.3)

(30.4)
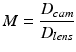
(30.5)

Fig. 30.4
Spatial variation of interference fringes and speckle envelope across a CCD chip. Optimum digital holography performance uses three interference fringes per speckle and three digital pixels per fringe
Equating the two magnifications gives a resolution
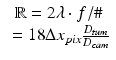
where the resolution is independent of the characteristics of the objective lens.
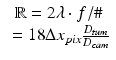
(30.6)
30.4 Multicellular Tumor Spheroids
In vitro monitoring of tissue response to drugs is an area of strong interest to pharmaceutical companies [61]. Although the in vitro environment is artificial, the biochemistry, metabolism, and cell signaling response of cells grown as 3D constructs closely simulates in vivo tissue because three-dimensional cell cultures have active 3D intercellular signaling pathways that are often absent in 2D dish cultures. Therefore, in vitro experiments are a validated (and inexpensive) surrogate for in vivo response. The most common in vitro tissue cultures are multicellular spheroids. Multicellular spheroids of normal cells or neoplastic cells (tumor spheroids) are balls of cells that may be easily cultured up to 1 mm in size in vitro [62–67]. The spheroids can be used to simulate the optical properties of a variety of tissues such as the epidermis and various epithelial tissues and may be used to simulate the histological and metabolic features of small nodular tumors in the early avascular stages of growth [67]. Since the introduction of the concept of multicellular tumor spheroids in the early 70s [68], 3-D aggregates of permanent cell lines have offered a reliable model for systematic study of tumor response to therapy [65, 69].
Beyond a critical size (about 100 μm), most spheroids develop a necrotic core surrounded by a shell of viable, proliferating cells, with a thickness varying from 100 to 300 μm. The development of necrosis has been linked to deficiencies in the metabolites related to energy generation and transfer. The limiting factor for necrosis development is oxygen – the oxygen consumption and oxygen transport reflecting the status of the spheroid [63, 70]. Early work [71] launched the study of therapeutic strategies for cancer. The response to drug therapy was quantified from analysis of spheroid volume growth delay, increase in the necrotic area, and change in survival capacity. This work focused on hypoxia and its induction by chemical agents [72].
Tumor spheroids are cultured in a rotating bioreactor (Synthecon, Houston, TX) where they were maintained in suspension. The spheroids may be grown up to several mm in diameter and are thus large enough to simulate the thickness of different mammalian tissue (skin epidermis is 70–120 μm thick over most of the human body). An advantage to using this continuous culture model is that fresh spheroids of varying size are easily prepared on a daily basis. Overall, the tumor spheroids provide a reasonable tissue model that does not require special handling of animal subjects.
Electron microscopy sections of two types of tumor embedded in Toluidine-blue-stained epoxy resin and sectioned at 1 μm thickness are shown in Fig. 30.5. The tumors are nearly a millimeter in diameter, and each shares a common morphology. The outermost layers of the tumors have healthy, proliferating cells that form a shell from 100 to 200 μm thick. These cells are in close proximity to the nutrients and oxygen of the growth medium. This layer is structurally homogeneous and is optically homogeneous as well. Deeper inside the tumors, the cells become apoptotic because of nutrient deprivation and oxidative stress from the diffusion limitation of nutrients and oxygen into these avascular spheroids. The apoptotic cells give way, deeper in the tumor spheroids, to necrotic regions characterized by voids of extracellular debris or by microcalcifications, which are especially pronounced in the osteogenic spheroids. The core is structurally heterogeneous and is optically heterogeneous as well. Therefore the tumor spheroids have the general morphology of a healthy outer shell that tends to be homogeneous and a core of necrotic regions that are spatially heterogeneous.
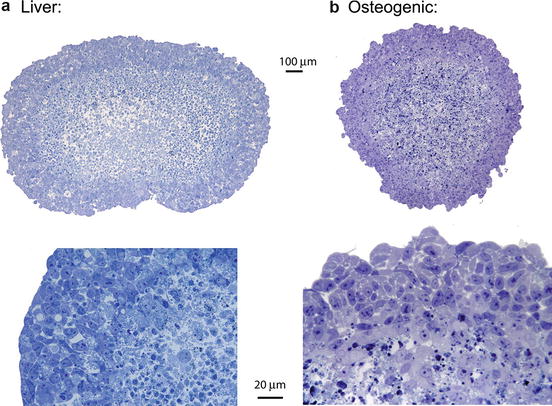

Fig. 30.5
Cross-sectional TEM micrographs of multicellular tumor spheroids consisting of (a) human liver and (b) rat osteogenic cells. The spheroids have an outer shell of healthy proliferating cells around a necrotic core. The higher magnifications at the bottom show the transitions from the shells to the cores
Experimentally measured reduced scattering coefficients μ’ of rat osteogenic tumor spheroids are on the order of 8 mm−1 to 15 mm−1. There is a weak tumor size dependence to the extinction coefficient with decreasing extinction with increasing tumor size. The phase function for two tumors of slightly different diameter is shown in Fig. 30.6a. A tumor with a diameter of 416 μm is fit best with an anisotropy factor of g = 0.9, and a slightly larger tumor with a diameter of 484 μm is fit with a smaller factor of g = 0.85. Therefore, the rat osteogenic tumor spheroids are relatively translucent tumors with strong forward scattering. Maps of the optical densities of several tumors are shown in Fig. 30.6b, obtained using coherent heterodyne transmission interferometry.
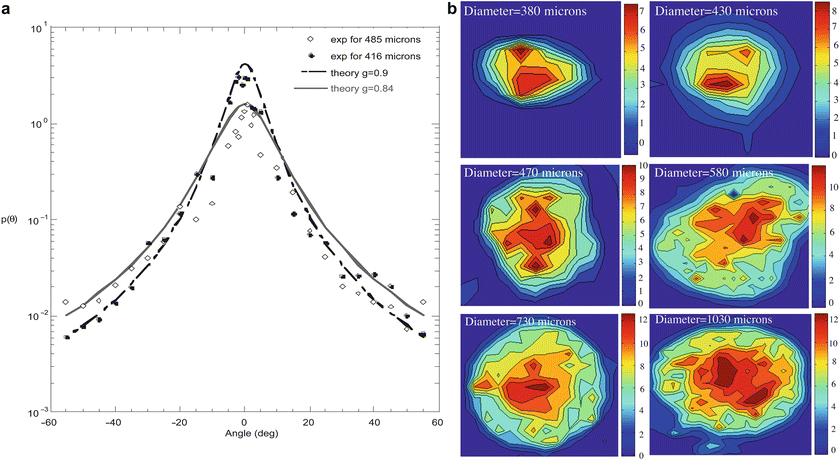

Fig. 30.6
Henyey-Greenstein phase function (a) and optical density maps (b). The HG functions were obtained using incoherent illumination in a forward-scattering arrangement. The optical densities were measured using coherent heterodyne detection of transmitted light
30.5 Photorefractive OCI of Tumor Spheroids
The principal acquisition mode for holographic imaging of tumor spheroids is called a “fly-through”. In this mode, the reference mirror is stepped by 10 μm, several successive images are averaged on the CCD camera and downloaded to the computer, the mirror steps again, and the process reiterates. The raw data are stored in a volumetric data cube of en face sections at successive depths from the top of the tumor through the bottom of the tumor (that usually sits on the surface of a Petri dish). Selected en face (called XY) sections of a 400 μm diameter tumor are shown in (Fig. 30.7a) separated by 23 μm (approximately equal to the longitudinal coherence length). The top of the tumor is at frame 15, and the Petri dish appears in frame 66. The tissue gray scale is logarithmic in a range from −50 to −85 dB. Alternatively, the data cube can be viewed laterally, giving pseudo-B-scans (called YZ sections), shown in (Fig. 30.7b) for the same tumor on logarithmic scale. The Petri dish is at the bottom of each YZ section. The distance between the selected sections is 26 μm (approximately equal to the transverse optical resolution for this data). The reflected intensities are brightest in the necrotic core, with relatively weak reflections arising from the homogeneous healthy tissue shell.
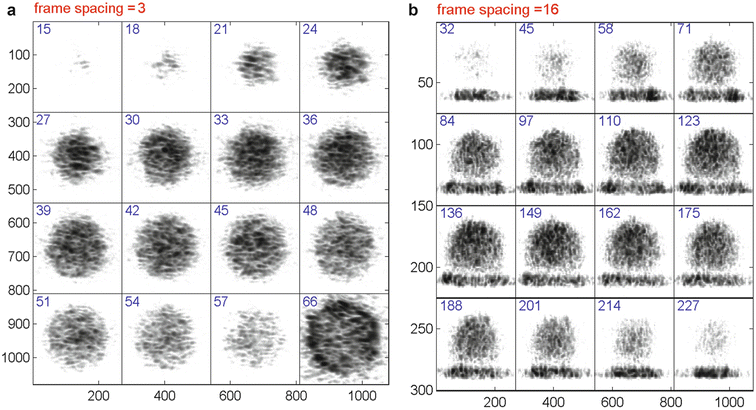

Fig. 30.7
Sections from a healthy rat tumor. Selected xy en face sections are shown in (a), and pseudo-B scans are shown in (b). The Petri dish reflection appears in frame 66 of the en face sections and at the bottom of the B-scan sections. The exposure time per frame was 0.5 s
The data for this tumor are visualized volumetrically in Fig. 30.8 for two selected threshold values of the isosurfaces. The left-hand figure has a low threshold and displays the full tumor volume with the Petri dish at the bottom. The right-hand figure has a high threshold to display only the brightest reflections from the tumor. The brightest features reside toward the center of the tumor, which is consistent with the necrotic core of the tumor spheroids. The necrotic core contains relatively large (10–20 μm) necrotic voids with extracellular debris as well as microcalcifications that are fairly pronounced in these osteogenic tumor spheroids. The heterogeneity of these internal structures are the likely source of the bright reflections that are localized internally to the tumor.
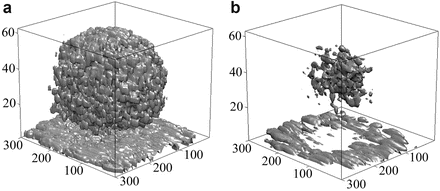

Fig. 30.8




Volumetric rendering of a tumor on a Petri dish. The image in (a) is the full isosurface, while in (b) a higher isosurface is shown. This illustrates the increasing intensity of reflections from the core of the tumor
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


