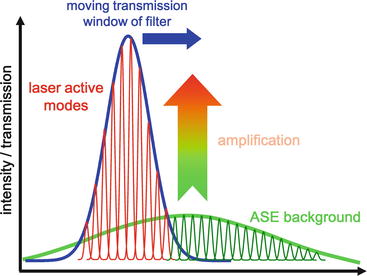
Fig. 24.2
Tunable laser buildup dynamics [14, 27]. The diagram shows the tuning operation of a standard wavelength-swept laser. As the transmission window of the optical bandpass filter (blue line) is moved in wavelength, the laser light field (red lines, laser modes) has to build up from amplified spontaneous emission (fluorescence) background (green). If the filter is tuned too fast, there is not enough time to build up saturated lasing – this effect limits the maximum achievable tuning speed
Typical numbers of short cavity lasers are resonator roundtrip lengths of about 0.3 m, yielding ∼1 GHz roundtrip frequency and an amplification factor in the gain medium of about a factor of 1,000×. If such a laser should be swept over a 100 nm wavelength range with 100 kHz sweep repetition rate (10 μs sweep repetition time) and a 0.1 nm wide spectral filter is used for tuning, light is only transmitted through the filter for about 0.1 nm/100 nm∗10 μs = 10 ns. So light in a 1 GHz (0.3 m length) laser resonator can only perform ∼10 roundtrips until it is blocked again. In this configuration 1000 kHz sweep rate would be the absolute maximum frequency of the laser, since for faster tuning, light wouldn’t even be able to finish a single roundtrip before the filter blocks the wavelength again. Strategies to further shorten the laser resonator lead to the problem that the resonator mode spacing, i.e., the optical frequency spacing of the “allowed” laser modes, spreads more and more, leading to a more stepwise, very coarse, and discrete frequency tuning characteristic [16]. The laser jumps from one mode to the next. For OCT application this is a major problem, because the maximum ranging depth of the OCT setup is directly linked to the spectral sampling density. When using classical tunable lasers for SS-OCT, the maximum imaging range cannot be longer than the laser’s optical roundtrip length.
Recently, strategies have been demonstrated to solve the problem of the increasing spectral spread (coarse mode hopping operation) of laser modes when reducing the cavity length. One approach, followed in the “akinetic OCT laser source” [17], is to insert an additional active element, a “phase section,” which allows to adjust the resonator length such that an “allowed” resonator frequency shifts synchronously with the laser tuning operation. The active synchronization requires complex electronic driving signals and repetitive resetting, blocking the source for ∼10 ns every 1 nm tuning.
Another approach to solve the problem of the increasing spectral spread of laser modes when reducing the cavity length is vertical-external-cavity surface-emitting laser (VECSEL) or often just called vertical-cavity surface-emitting laser (VCSEL) [18–25] (Chap. 22, “VCSEL Swept Light Sources”, Jayaraman). In these lasers, the laser cavity acts as Fabry-Perot filter with a very wide free spectral range (optical frequency spacing between two laser modes) with the effect that the laser resonator modes are automatically always synchronously tuned to the laser sweep operation. Additionally, light in the laser resonator is Doppler shifted each time it is reflected from the moving laser end mirror; this solves the problem of the repeated buildup of laser light from ASE. The Doppler shift has always the right amount to match and synchronize to the tuning operation. A more detailed description of the intracavity Doppler shift and calculations is given by A. Siegman in the book Lasers [26].
24.2 Fourier Domain Mode Locking (FDML)
24.2.1 The Concept
The technique of Fourier domain mode locking (FDML) is one way to overcome the physical limitation of cavity buildup dynamics. The idea behind it is to synchronize the optical roundtrip time of light circulating in the laser cavity with the filter sweep operation period of the optical bandpass [14, 27, 28]. This means one tuning period of the laser takes exactly as long as the light needs to propagate through the laser cavity. In other words, light with a certain wavelength is transmitted through the optical bandpass filter and then propagates through a very long laser cavity, realized by an optical delay line. Meanwhile the optical bandpass filter is swept over one entire cycle, covering all desired wavelengths, and just when the light arrives back at the filter, the filter transmits this wavelength again, but now already for the next wavelength sweep. This means light does not have to build up from ASE background; it is still there from the last wavelength sweep. In other words, the entire wavelength sweep is optically stored inside the laser cavity. The setup of an FDML laser is identical to a regular swept laser, besides an additional very long optical delay line. Since sweep repetition rates of fsweep = ∼100 kHz require optical path length of ΔL = c/fsweep = c/100,000 Hz = 3 km, usually a spool of optical single mode fiber is used. To make all wavelength components circulate at the same frequency, the chromatic dispersion of the fiber delay lines has to be compensated. The better the compensation, the higher the number of effective roundtrips of the photons inside the laser and the better the performance of the swept source [29, 30] (Fig. 24.3).
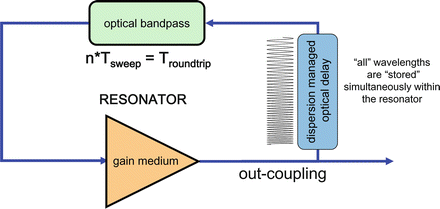

Fig. 24.3
Circuit diagram of an FDML laser [27]. An FDML laser consists of the same elements as a standard tunable laser plus an additional optical delay line (usually a km long fiber spool) to generate the long roundtrip times
The synchronization condition of FDML operation leads to the effect that the light of a certain wavelength sees the spectral optical bandpass filter always in the same position (see Fig. 24.4, right), whereas in a standard tunable laser, light always is transmitted through a slightly changing filter (see Fig. 24.4, left). The fact the periodic operation makes the filter look “non-tuned” for the light results in a stationary operation of the FDML laser (see Fig. 24.4, right) [36].


Fig. 24.4
Quasi-stationary filter in FDML operation. Left: Nonstationary operation of a standard tunable laser with a sinusoidally driven filter (black line). As light of a certain wavelength arrives at the filter after one roundtrip, the filter has changed its spectral position (black line). Right: In case of FDML the optical roundtrip time is increased so much that when light of a certain wavelength arrives back at the filter after one roundtrip, the periodically driven filter is at exactly the same position (but at the next cycle). This makes FDML a real stationary operation mode
24.2.2 Advantages of FDML
The system design and the fact that FDML is a stationary laser operating mode yield many advantages which dramatically improve the performance of the swept laser and, consequently, the OCT system specifications:
1.
The high number of effective roundtrips leads to the effect of repetitive spectral filtering (mode competition) making the spectral linewidth of FDML laser much narrower than the one of standard tunable lasers with the same filter width [27, 29–33]. The narrower linewidth improves the roll-off performance in OCT applications, resulting in a longer ranging depth [29, 30, 34, 35].
2.
The fact that the laser light is seeded from the last roundtrip and that FDML is a real stationary laser operating regime reduces the relative intensity noise (RIN) of the laser [29, 32, 33, 36–38], which makes it much easier to design a high-speed OCT system that achieves shot noise-limited sensitivity [39].
3.
4.
The separation of laser gain medium and filter element in FDML enables much more flexible system designs compared to VCSEL sources and standard tunable lasers. In both latter cases, the gain medium has to be very short, so typically only semiconductor media can be used. In FDML, almost all groups of laser gain media can be used with length up to meters, such as rare earth-doped fiber amplifiers, nonlinear Raman amplifiers, etc. [44–51]. This enables a much more flexible design of the target wavelengths; improves, as already mentioned, the achievable output power by orders of magnitude; and can dramatically reduce ASE background noise.
5.
24.2.3 The Name FDML and Other Lasers with Resonant Frequency Modulation
24.2.3.1 FDML Compared to Continuous Wave (CW) Lasers and Standard Mode-Locked Lasers
From a viewpoint of physics, FDML lasers are very different from other tunable lasers, because in FDML, the light field of the entire wavelength sweep is optically stored inside the laser resonator. So effectively, a wide range of laser modes is simultaneously active. In comparison, standard wavelength-swept lasers have only one or very few wavelength modes simultaneously active inside the resonator. The situation is sketched in Fig. 24.5. On the left and in the center, the two classical stationary laser operating regimes are shown. On the top is the emitted electric field and on the bottom the corresponding spectrum, which is essentially the squared amplitude of the Fourier transform of the field. A standard narrowband cw laser ideally has a harmonic wave output (Fig. 24.5, left top); the spectrum is a narrow peak (Fig. 24.5, left bottom). A classical mode-locked laser [52], like a femtosecond titanium sapphire laser, has an electric field output representing a train of short pulses (Fig. 24.5, center top), and the corresponding spectrum has a comblike structure with a wide spectral range (Fig. 24.5, center bottom). If this frequency comb is stabilized and the absolute position of each individual comb line is known, a wealth of applications in metrology and sensing can be realized [53]. An FDML laser has an almost constant output power (Fig. 24.5, top right) as the cw laser has; however the output spectrum is broad and has, in the ideal case, a comblike structure. This can be understood, since the FDML wavelength sweep can be considered as highly chirped pulse [54].
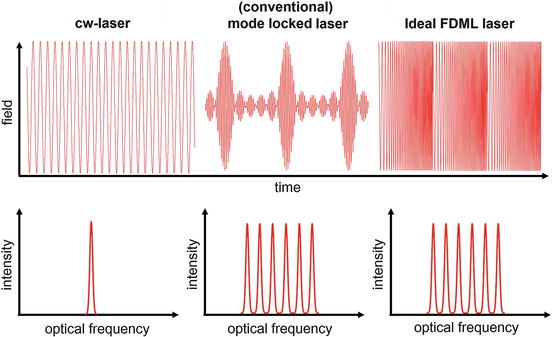

Fig. 24.5
The three stationary laser operating regimes. Electric fields (top) and spectra (bottom) of (left) a narrowband continuous wave (cw) laser, (center) a standard mode-locked laser, and (right) an FDML laser
Remark: It should be noted that the FDML output is in principle identical to the one of a so-called FM laser; however the experimental setup of both lasers is very different – the FM lasers [55] use NO filter and the intracavity element, which is a phase modulator, is driven OFF resonance.
The difference between the standard mode-locked laser and the FDML laser is that the phase of the individual modes with respect to each other is different. It should be noted at this point that currently it seems very difficult to measure the absolute position of the FDML comb line, so it cannot be expected that FDML lasers can be used for the same metrology and sensing applications like standard mode-locked lasers. However, the emission of an FDML laser spans 100 nm or more, proving that many individual modes are simultaneously active.
24.2.3.2 The Name “Fourier Domain Mode Locking”
Table 24.1 shows a comparison of FDML [27] to standard mode-locked lasers [52] which usually generate a train of ultrashort laser pulses. In standard mode-locked lasers, an active (e.g., an acousto-optic modulator) or a passive (e.g., transient Kerr lens, saturable absorber) amplitude or phase modulator modulates the intracavity light field synchronously to the optical roundtrip time. It acts like a shutter which transmits light only over a very short period of time, and only a short electromagnetic wave packet that arrives always at the modulator when the modulator has high transmission or low absorption can continuously circulate in the laser cavity. A time gate or a “time window” is applied. The output is a short pulse with minimum chirp. In FDML a “wavelength window” is applied, also synchronous to the roundtrip time, so it acts in the “Fourier domain” – actually the term “frequency domain” would be more accurate. The FDML output is, as described, a wavelength sweep, which is equivalent to an extremely chirped pulse. This equivalence has been shown by compressing the FDML sweep time [54]. The instantaneous spectrum of a standard mode-locked laser is wide, given by the time bandwidth limit – in an FDML laser, the instantaneous spectrum is narrow. Because both types of laser emit a train of light fields where each pulse or sweep is a copy of the previous one, there is a more or less pronounced phase relation between the pulses or sweeps. So overall FDML has the same synchronization condition as standard mode-locked lasers; however the modulator does not operate in the time domain but in the Fourier (frequenc<) domain, physical quantities that are short in standard mode locking are long in FDML, and quantities that are wide in standard mode locking are narrow in FDML, so in most parameters the FDML characteristic resembles the Fourier transform of a standard mode-locked laser. FDML is complementary to standard mode locking “linked by Fourier transform.”
Standard mode locking | FDML | |
|---|---|---|
Modulation frequency | Synchronous to roundtrip time | Synchronous to roundtrip time |
nature of modulation | Phase/amplitude | Spectrum |
Time domain | Fourier domain | |
Output | Short pulse | Long pulse (sweep) |
Minimum chirp | Maximum chirp | |
Instantaneous | Broad | Narrow |
Phase relation | Fixed (locked) phase relation between modes and pulses | Fixed (locked), but different, phase relation between modes and pulses |
24.2.3.3 Are the Modes in FDML Laser Locked?
The term mode locking in lasers is used, if there is a certain phase relation between the different cavity modes of the laser. For example, if thermal light or light from an amplified spontaneous emission (ASE) source is transmitted through a comb filter, like a Fabry-Perot, the output has also a comblike structure with multiple peaks, but with no phase relation between the different modes. If the spectrum of the light would be measured at a certain time, it would always contain all wavelength components. To generate a situation like in FDML, where at one certain point in time, only a very narrow range of wavelength can be measured, a phase relation between the different modes is required that generates destructive interference between all components, except the narrow range that is active at one moment in time. So already the fact that FDML lasers emit wavelength-swept light proves a certain phase relation between the different wavelength components.
A similar argument is analog to standard mode-locked lasers. In standard mode locking, the amplitude modulator, a type of “shutter,” is operated ideally with a very short duty cycle of, e.g., 1 %. So 99 % of light with an arbitrary phase is absorbed when coupled into the modulator. Now if the modulator is used in a mode-locked laser, where it is driven synchronously to the optical roundtrip time, the cavity modes develop a phase relation amongst each other and almost 100 % of the circulating light field is transmitted. The same is true for typical FDML lasers. The optical bandpass filter has a typical transmission window of about 0,1 nm, and the emission is about 100 nm. If ASE light is coupled into the filter, 99.9 % is back reflected. In FDML operation, we observe at maximum only about ∼10 % back reflection, because at each point in time, only modes within the transient spectral filter window interfere constructively.
So already the fact that the FDML laser emits wavelength sweeps and that the intracavity bandpass filter dissipates by orders of magnitude less light than its spectral fill factor proves that there is a certain phase relation between the different modes.
So there is a phase relation between the FDML cavity modes; however, how good this phase relation is, meaning how large the phase jitter between these modes is, is currently investigated. Theoretical models and numerical simulations provide access to the electric field [32, 33, 36–38]. Direct linewidth measurements in comparison with the theoretical results prove the model of FDML as a stationary operation, because the theoretical models show that FDML lasers continue to operate even without ASE noise. Initially there was a problem numerically simulating FDML operation, because of the wide wavelength sweep range of about 20 THz and the close mode spacing of about 100 kHz which would require an enormous number of simulation points. However, the introduction of a simulation strategy using a sliding reference frame reduced the number of simulation points and enabled successful numerical models describing FDML [32, 33, 36–38].
Very recently, the successfully compression of light from an FDML laser also give access to the internal phase conditions [54]. Simulations with a complementary approach supported by experiments indicate that mainly dispersion in the FDML laser cavity deteriorates the phase relations, i.e., the “mode locking” [56].
24.2.3.4 Other Lasers with Frequency or Phase Modulation
There are other types of lasers that modulate the phase and frequency of the light field inside the laser cavity which are often confused with FDML. However, these lasers are technically very different to FDML. To avoid this confusion, the reader finds some explanations about these different technologies in the following.
FM Mode Locking
FM mode locking [57] is often confused with FDML because of the similar acronym. FM mode locking has been known since the 1970s, and it is used to generate short laser pulses, not wavelength sweeps. FM mode-locked lasers have a phase modulator and not an optical bandpass filter inside their cavity. The phase modulator is driven synchronously to the optical roundtrip time in the cavity. It is often discussed that a more accurate term for FM mode-locked lasers would be “phase mode-locked” lasers. Unlike an FDML laser, an FM mode locking laser does NOT have a tunable optical bandpass filter.
FM Lasers
An FM laser [55] is a laser with a setup identical to the FM mode-locked laser; however, the phase modulator is driven off resonance. By this strategy, transient wavelength sweeps can be generated. FM lasers generate one wavelength sweep per optical roundtrip time, similar to FDML; however FM lasers don’t have an optical bandpass filter and their sweep range is usually limited to a few nm due to the lack of suppression of ASE. Also FM lasers usually exhibit a breathing of the spectrum. Unlike an FDML laser, an FM laser does NOT have a tunable optical bandpass filter.
Wavelength Tunable Laser with Resonant Frequency Shifting
FDML operation is also often confused with wavelength-swept lasers which incorporate an optical frequency shifter [58]. Such lasers have been demonstrated with sweep repetition rates up to ∼1 kHz. The frequency shifter’s purpose is to also overcome the fundamental problem of the required repetitive buildup of lasing during sweep operation. The light inside the cavity is shifted exactly by the amount that is required to compensate the filter tuning operation. In other words, light which is transmitted through the filter is frequency shifted on its way through the cavity, and when it arrives back at the filter, the new wavelength matches exactly the new position of the optical bandpass filter. The problem with this design is that the amount of frequency shift achievable with current devices is hardly more than 1 GHz and it is therefore not sufficient for very fast tuning operation. Unlike an FDML laser, a resonant frequency shifting laser does NOT synchronize the optical roundtrip time with the filter tuning period of the optical bandpass filter.
Very Rapid Tuning of CW Dye Laser
In 1975 Telle and Tang [28] demonstrated a tunable laser using an electro-optical element acting as a type of optical bandpass filter. The concept of this approach is the same as in FDML; however, no narrowband wavelength filter was applied, and with a tuning range of 2 nm and a linewidth of 0.2 nm at a repetition rate of 100 MHz, this source cannot be used for OCT.
24.3 Milestones in FDML Development
24.3.1 The First Implementation of an FDML Laser
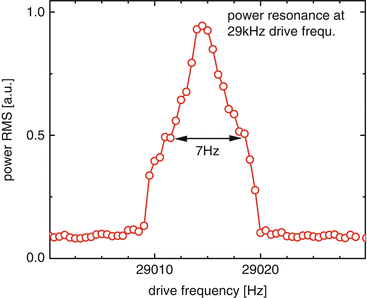
Figure 24.6 shows the first implementation of an FDML laser for OCT in 2005 [59]. The laser is implemented in a ring geometry using a fiber-based resonator. The laser gain medium is a fiber-pigtailed packaged semiconductor optical amplifier (SOA) from Inphenix, Inc. The tunable optical bandpass filter is a Fiber Fabry-Perot Tunable filter (FFP-TF) (Micron Optics, Inc.). A spool with 7 km standard single mode telecom fiber (Corning SMF 28e) provided the optical delay of 34 μs. Figure 24.7 shows the output power of the laser for different values of tuning frequency of the optical bandpass filter. It can be seen that only for a very narrow range of filter drive frequencies ffilterdrive, the FDML condition ffilterdrive = c/l is fulfilled. The resonance has a width of about 7 Hz at a center of 29,015 Hz corresponding to a system finesse of 1/4,000.
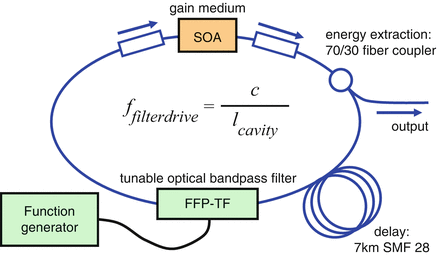

Fig. 24.6
Setup of first FDML laser [59]. SOA semiconductor optical amplifier. FFP–TF Fiber Fabry-Perot Tunable filter. Arrows Optical isolators, ensuring unidirectional lasing and blocking light that is back reflected from the FFP-TF. SMF 28 Standard optical single mode fiber
As seen in Fig. 24.7, the laser resonator has an optical roundtrip frequency of 29 kHz. Since the Fabry-Perot Tunable filter is preferentially driven sinusoidally at such high speeds, two wavelength sweeps are generated for each drive cycle of the filter. So driving the filter with 29 kHz generates 29,000 forward (shorter to longer wavelength) sweeps and 29,000 backward sweeps per second. For OCT application, 58 kHz line rate is possible.
Obviously this laser can also be driven with higher harmonics, i.e., two or more sweeps are simultaneously active in the FDML laser. The laser has resonances at 2 × 29 = 58 kHz, at 3 × 29 kHz = 87 kHz, and so on. In the first demonstration in 2005, up to 290 kHz sweep rate had been demonstrated.
24.3.2 Buffering: Increasing the Sweep Speed by Optical Time Multiplexing
Conceptionally, FDML lasers have no speed limit as long as the intracavity tunable bandpass filter supports the high sweep speeds. It actually turns out that FDML lasers are more stable at higher speed, because the required delay fiber length is shorter for higher frequencies. This reduces thermal drift effects and problems with unstable polarization [29, 60].
However, the availability of fast tunable optical bandpass filters with the required specifications is limited. The filters should have <0.15 nm passband, >120 nm free spectral range, and >40 dB out of band rejection. Currently, at sweep speeds of more than 100 kHz, only Fabry-Perot filters achieve this type of performance. Custom-built research devices achieve up to 2 × 419 kHz [61], and commercially available devices achieve 2 × 170 kHz (Lambdaquest, Inc.). This is typically the highest mechanical resonance frequency with sufficient response. However, the achievable tuning amplitude in these resonances is typically much larger than the lasing range, even larger than one free spectral range. So the total tuning speed measured in nm/μs can be increased by increasing the amplitude.
The technique of sweep buffering [62] can convert excess sweep amplitude to sweep frequency. It is used to convert lower filter sweep frequencies with a high amplitude to high sweep frequencies with lower amplitude. Figure 24.8 shows the setup of an 8× buffered FDML, and Fig. 24.9 shows the concept of sweep buffering in the case of 4× buffering. In the setup in Fig. 24.8, a 325 kHz FFP-TF is used. The filter is driven with such a high amplitude that the duty cycle of one forward sweep is only 12.5 %, and the rest of the time over one entire sweep cycle the SOA is switched off. The sweep output is now coupled into a cascade of splitters and recombiners, each with an additional length of fiber in one arm. The length of this arms is one half, one fourth, and one eight of the cavity length. This leads to multiple copies of the sweep, here 8. After the last coupler, there are two outputs, each with 8 × 325 kHz = 2,600 kHz sweep rate. Figure 24.9 shows the individual steps for a 4× buffered FDML with the steps of overdriving the FFP-TF, generating a short duty cycle, ON-OFF modulation of the SOA, copying and delaying the individual sweeps. It should be noted that sweep buffering is not limited to FDML lasers; it can be applied to all lasers that have excess tuning rate and short duty cycle [63].
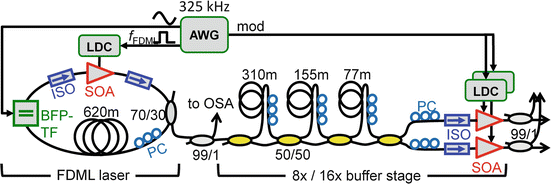
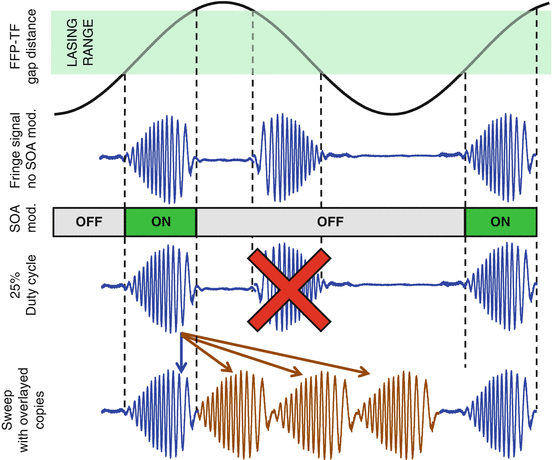

Fig. 24.8
Setup of a 2,600 kHz 8× buffered FDML laser [43]. Example of a buffering setup to multiply the sweep rate. The 2 × 325 kHz FDML is scaled to 2.6 MHz sweep repetition rate. The output is split, a part is delayed, and then the light is recombined

Fig. 24.9
The concept of buffering in case of an FFP-TF [62]. Here the situation for an FFP-TF filter buffering by a factor of 4× is shown. The sweep amplitude is increased to achieve a short duty cycle of the lasing operation, in this case 25 %. The laser gain SOA is switched off over 75 % of the time, and one sweep direction remains. The 75 % gap is filled with copies of the original sweep. The resulting sweeps have a 2× higher sweep rate and are unidirectional and highly linear in optical frequency and groups of four are almost mutually identical
The main reason for sweep buffering is to increase the repetition rate of FDML or standard swept lasers [30, 34, 62–71]. However, there are numerous additional advantages of buffering. The most important one is that there is an almost perfect optical phase relation between the different copies of the sweep, making them the ideal source for phase-sensitive and Doppler OCT imaging [68, 69].
Another advantage is that wavelength over time tuning characteristics and also the optical frequency over time tuning characteristics of the light sources’ output is usually much more linear than in standard FDML lasers. The reason is that the FFP-TF filter in FDML lasers is usually driven in a mechanical resonance sinusoidally which leads to a very slow tuning operation near the turning points. On one hand, such a huge variation in filter sweep speed is problematic from an engineering viewpoint for an OCT system, because the resulting fringe frequencies span a very wide range of RF frequencies from the photo-receiver. This requires systems with a very flat electronic phase response. On the other hand, the very slow tuning speed at the turning points at a constant exposure level adds up to the total amount of optical power on the sample, but only very few data points are collected right at the turning points, considering the equidistant optical frequency grid before FFT in SS-OCT/ODFI. This means a lot of energy is put on the sample, but very little information is acquired. So sweep buffering improves linearity which can simplify OCT system design and improve image quality.
A further advantage of sweep buffering is that the polarization state of the different sweeps can be passively controlled. For many PS-OCT applications, a sequence of wavelength sweeps with alternating polarization state is required [72, 73]. This is usually realized by active optical elements with the problem of synchronization, additional differential polarization-dependent group delay, and dispersion. With the technique of sweep buffering, different polarization states can be generated passively [60].
For these reasons, buffering stages are an integral element in many of the most advanced MHz FDML lasers.
24.3.3 The Second-Generation FDML Lasers: Dispersion Compensation
The idea of FDML is to synchronize the optical roundtrip time of light in the laser cavity with the filter tuning period. But this would require that all the different wavelength components of the FDML laser propagate with the same speed. Due to chromatic dispersion in the delay fiber, this is not the case which leads to a more or less pronounced miss synchronization for some wavelengths [29]. The first FDML lasers have been implemented at a center wavelength of ∼1,310 nm. This is the zero dispersion point of standard optical fiber, meaning in a narrow range around 1,310 nm, all wavelengths propagate at the same speed. However, zero dispersion point means only that there is no linear group velocity dispersion (GVD) (i.e., second-order dispersion), so no term measured in ps/(nm∗km). However there still is remaining GVD slope measured in ps/(nm2 ∗km). And because typical OCT lasers sweep over a very wide spectral range of 100 nm or more, this has a significant effect on the roundtrip time. Figure 24.10 (left) shows the difference in roundtrip time for the various spectral components in a 100 kHz 1,300 nm FDML laser (2 km fiber).
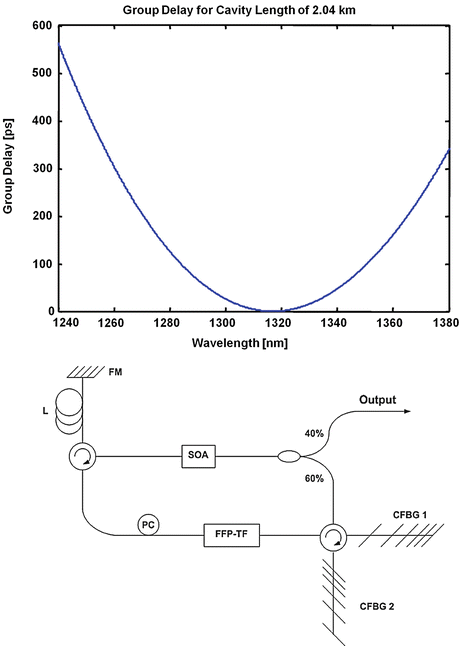

Fig. 24.10
Dispersion in FDML and compensation setup [30]. Top: Propagation time difference for the spectral components in a 100 kHz FDML laser cavity [30]. Bottom: Setup of an FDML laser with compensated chromatic dispersion. The laser uses two custom-designed chirped fiber Bragg gratings (cFBG) from Teraxion, Inc
It can be seen that light with 1,240 nm has a 550 ps longer propagation time through the cavity than light with 1,320 nm. At a roundtrip time of 10 μs, this is a synchronization error of 50 ppm (5e-5) which is small enough that it doesn’t affect the output power of the FDML laser. However, it also means that light will not circulate in the FDML cavity forever; after a certain number of roundtrips, the timing offset will be large enough that the light is blocked by the filter. In the shown case, this reduces the number of roundtrips of the intracavity photons in the FDML laser to approximately 12 at the very edges of the spectrum [30]. This negatively affects the instantaneous linewidth of the FDML laser reducing the instantaneous coherence length. For this laser the practical single-sided OCT ranging depth is reduced to about 5 mm, i.e., the OCT depth range over which almost no signal decay can be observed. The effect of chromatic dispersion is even more severe in FDML lasers at 1,050 nm as used for retinal imaging. There the chromatic dispersion of optical fiber has a substantial linear contribution of ∼40 ps/(nm∗km).
The solution to this problem is to compensate the intracavity dispersion of the FDML. The different approaches that have successfully been demonstrated are the use of a wideband zero dispersion photonics crystal fiber [64, 75], the use of a sequence of different fibers to cancel out the dispersion contributions of the individual pieces [29, 76], and most recently the application of chirped fiber Bragg gratings (cFBG) [30, 34, 35]. A cFBG is a piece of fiber with a periodic refractive index modulation where the period changes over length. This way, light with different wavelengths is reflected in different depths yielding a wavelength-dependent propagation time. The cFBGs can now be designed in a way that they exactly compensate the chromatic dispersion of the FDML cavity. Since usually cFBGs are preferred with a monotonic group delay over wavelength, a pair of matched cFBGs is used at 1,320 nm, because the dispersion zero of standard optical fiber leads to a minimum of propagation time. Figure 24.10 (right) shows the setup of a compensated 1,300 nm FDML, and a 4-port circulator is used in the light path to generate the two reflections from the cFBGs. The pair of cFBGs was designed and manufactured by TeraXion, Inc. (Quebec City, Canada). Figure 24.11 (left) shows the group delay of the two cFBGs and the total group delay. Starting from more than 200 ps timing error for the different wavelength components of a 100 nm range, less than 4 ps remain after compensation (Fig. 24.11 right); this is a reduction of more than 50×. The relative timing error of 4 ps compared to the 10 μs tuning period corresponds to a relative error of 400 ppb (4e-7). This value theoretically enables several 1,000 roundtrips of light in the cavity [30].
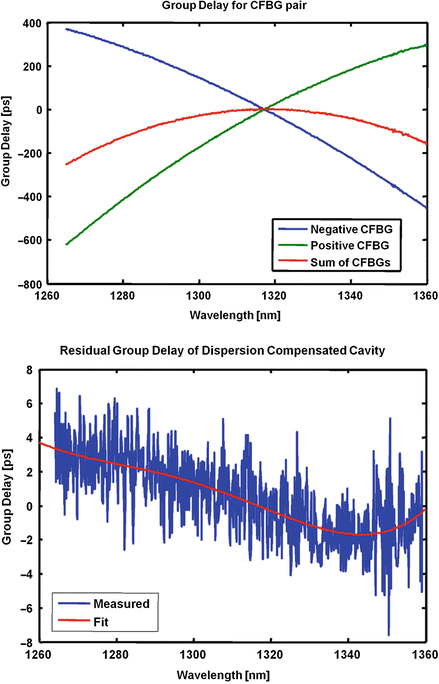

Fig. 24.11
Dispersion compensation with chirped fiber Bragg gratings (cFBGs) [30]. Left: A combination of two cFBGs can generate a net GVD slope value. Right: The dispersion is reduced by almost a factor 50
Because of this higher number, light is effectively filtered more often improving the instantaneous linewidth. The sensitivity roll off is reduced; the OCT system ranging depth improved to more than 10 mm (>21 mm 6 dB coherence length). Figure 24.12 shows the improvement; the point spread functions are plotted over OCT imaging depth. For the non-compensated FDML, a 6 dB roll off over 5 mm is observed. Using dispersion compensation this value is more than doubled. The measurements in Fig. 24.12 may have been limited by the detection electronics rather than by the laser linewidth properties, so the real roll-off performance of this laser can be even much better. This increase in total OCT imaging range is most important for applications in intravascular imaging, where a >5 mm range is usually desired to better image some anatomic features like arterial branches [30].
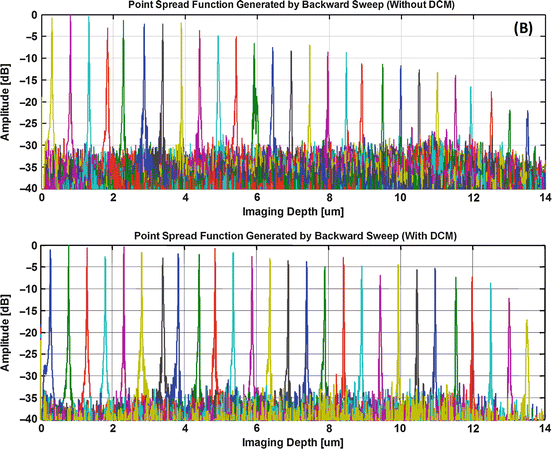

Fig. 24.12
Improved roll-off performance by dispersion compensation [30]. Top: Point spread function (PSF) over imaging depth for an OCT system using a standard 2 × 100 kHz 1,300 nm FDML laser. A 6 dB signal roll off over 5 mm can be seen. Bottom: Roll off for the same laser with additional dispersion compensation – the 6 dB signal roll off is extended to >10 mm
24.4 Different Variations and Implementations of FDML
Since in FDML both of the critical elements of a tunable laser are separated and because they can have substantial optical path length, FDML allows many different combinations of gain and filter media to specifically tailor them towards the application of interest.
Besides the typical SOA gain medium, FDML lasers has been built with Raman gain for extremely low ASE background noise [51], with rare earth-doped fiber amplifiers [44, 45, 47] for very high output powers, with nonlinear post conversion [77] or optical parametric amplification [47, 48, 78] for very flexible gain regions and with combinations of these different techniques.
The tunable filters used for FDML lasers have been limited to very rapidly tunable ones. In most cases Fabry-Perot Tunable filters are used, but also polygon scanner-based systems are possible and have a number of advantages, like inherent unidirectional sweeping and very high-power handling capabilities [79].
Stabilization of FDML operation is usually performed by active or semi-passive mechanisms, solving the problem of drift in FDML.
24.4.1 FDML with Raman Gain
Due to their setup with a long length of fiber, FDML lasers offer the ideal starting point for Raman amplification as laser gain process [46, 49–51]. Raman amplification in fibers is widely used, because the small mode field diameter in optical single mode fibers over a very long interaction length compensates for the very small Raman scattering cross section. The advantage of Raman gain is the potentially very flexible range of operating wavelengths and the good noise performance. It has also been used to study the photon life times and loss mechanisms in FDML lasers [51].
24.4.2 FDML with Erbium Fiber Gain
In the 1,550 nm wavelength range, which can also be used for OCT, especially if samples with low water concentration are imaged [15], an erbium-doped fiber amplifier (EDFA) can be used instead of an SOA as gain medium [47, 48]. EDFAs have also a better noise performance than SOAs, and they can achieve higher output powers. Disadvantages of EDFAs are the smaller amplification bandwidth and the tendency to Q-switch because of the long carrier lifetime of ∼20 ms. If EDFAs are used for fast swept lasers and the sweep rate is increased, carrier relaxation oscillations get stronger and high output intensity fluctuations are observed. At some point the laser goes into Q-switching mode emitting a sequence of pulses. Due to the high power of such pulses, they can destroy the intracavity filter.
24.4.3 FDML with Ytterbium Fiber
At 1,050 nm an ytterbium-doped fiber amplifier (YDFA) can be used as amplification element [44–46]. In [45] this was used in combination with an SOA. YDFAs have the advantage of good noise performance and the capabilities for very high-power output. Their gain profile covers an extremely wide wavelength range of much more than 100 nm around 1,050 nm.
The output powers achievable with YDFAs are scalable into the Watt region. Figure 24.13 shows the case for an FDML laser used for retinal imaging. Considering the duty cycle of this laser, the peak power was larger 400 mW. Especially since in the 1,050 nm region swept laser sources often do not exhibit sufficient output power, YDFA-based FDML lasers appear very attractive.
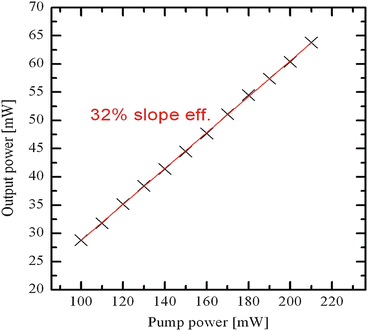

Fig. 24.13
Output power of 1,050 nm FDML using YDFA. The average output power of the FDML can easily exceed 60 mW. At duty cycles of 12.5 % for 8× buffering and a Hanning shaped spectrum, this corresponds to >400 mW peak power of the wavelength sweep
24.4.4 FDML Polygon Scanner Filters
Even though in most cases FDML lasers are built with FFP-TFs, the FDML concept is not linked to a special type of optical bandpass. Leung, Liu, and Mao et al. demonstrated an FDML laser using a grating filter based on a polygon scanner [40–42, 79]. The advantages of this device are unidirectional scanning operation and very good sweep linearity without buffering.
24.4.5 FDML with Regenerative Mode Locking
One problem of FDML operation, especially if an FFP-TF is used, is the control and automatic stabilization of the wavelength sweep filter. Sweep amplitude, offset, and frequency have to be controlled; thermal drift has to be compensated. Different active control loops have been demonstrated. A very interesting concept is the application of a regenerative mode locking concept [79]. The optical output of the FDML laser is used to control an electronic signal that drives the filter. This way, temperature-dependent changes in the optical roundtrip frequency are automatically compensated for, and the laser always finds the best frequency.
24.5 The Performance of FDML Lasers in Comparison to Other Light Sources
24.5.1 Competing Technologies
At the time of the first introduction in 2005, the performance of FDML lasers was quite unique, and hardly any other technology could achieve the combination of sweep speed, linewidth performance, and spectral sweep range. However, over the last few years, other swept source technologies have been developed that now approach and may even exceed FDML performance in some aspects. In the following sections the state of the art in the year 2013 will be shortly reviewed with respect to performance characteristics of these new sources compared to FDML. Currently there are many promising ideas and concepts for fast wavelength-swept light sources intended for use in OCT, but in several cases, it has not finally been proven, whether these sources can really achieve good imaging performance in biomedical applications [17, 80–82]. So here the focus lies only on three non-FDML techniques and light sources where OCT imaging has already been demonstrated at speeds in excess of 200 kHz, because the high sweep speed performance is the most outstanding characteristics of FDML laser.
The first class of high-speed swept light sources are lasers where the cavity length is reduced so far that the lasing buildup dynamics is fast enough to achieve high-speed tuning. Since this class of sources does not solve the problem of laser buildup dynamics, it can be expected that they are not arbitrarily scalable to higher speeds and probably only several 100 kHz sweep rates are possible, in case other typical OCT performance criteria are maintained. It should be noted that a reduction of the laser resonator cavity length in classic swept laser designs using a separated gain medium and an optical bandpass filter is only possible up to a certain amount. Since the cavity length defines the mode spacing of the laser resonator and this mode spacing becomes larger as the laser resonator length is decreased, the possible spectral sampling density becomes coarser. In other words, if the cavity length of a linear laser resonator is, e.g., 5 mm, the optical mode spacing of the resonator modes is Δf = c/2 l = 30 GHz. At 1,300 nm wavelength, this corresponds to 0.17 nm spectral separation which is, in OCT application, the best achievable spectral sampling density. This corresponds to an OCT imaging range of 2.5 mm. So with a standard laser, it is not possible to build an SS-OCT/OFDI system that has a single-sided ranging depth of more than the laser cavity length. In reality, the laser resonator length is typically chosen significantly longer to avoid beat noise between individual modes. Therefore highly integrated short cavity lasers have the laser end mirror outside the package in the fiber pigtail, resulting in typical cavity roundtrip lengths 30 cm, about 1 GHz optical mode spacing. According to the single roundtrip limit presented in [14], it can be expected that such lasers are limited to <300 kHz sweep rate if a 0.05 nm linewidth and 100 nm sweep range are chosen. The problem of discrete mode spacing may theoretically be overcome by advanced variable cavity designs or an active phase section in the laser resonator, as used in telecom applications [17]. However, the laser dynamics at fast sweep operation and the influence on OCT image quality have not been investigated yet. The most prominent examples of fast short cavity lasers are the ones from Oh et al. [63] as research systems and the ones from Axsun technologies [84] and Santec [85]. A more detailed discussion of this laser type can be found in ..” reference to Bart Johnson (AXSUN), Bill Ahern chapter in this book.
The second class of successful high-speed tunable lasers are mechanically tunable vertical-external-cavity surface-emitting lasers (VECSEL) (see Chap. 22, “VCSEL Swept Light Sources”). These devices can achieve very fast tuning operation. It is often argued that the short cavity length of these devices promotes very rapid buildup. However, the most recent results showing meter long coherence lengths, equivalent to >10 ns coherence time, are not possible at the typical sweep rate of >>1 GHz/ns tuning if lasing is repetitively built up, since this would violate the time bandwidth product. So the reason for the good coherence performance at high tuning speed is that the Doppler shift caused by the reflection of light from the moving end mirror automatically adjusts the wavelength of the light field such that it always matches the resonance condition of the tuned laser cavity. The calculation can be found in [26]. For this reason, VECSELs have also no fundamental tuning speed limit.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree