(39.1)
In this expression, the mean squared field, E, as a function of scattering angle, θ, is related to the two-point density correlation function, Γρ(r), of the sample as a function of separation, r, along the direction given by the scattering angle θ.
An alternative to analytic approaches is to numerically solve Maxwell’s equations for a range of scattering geometries and then compare a measured distribution to a database of simulated values. Frequently, Mie theory has been used because it can rapidly produce exact scattering solutions for spherical scatterers and approximately correct solutions for nearly spherical scatterers. Surprisingly, even moderately aspherical objects such as the nuclei of many types of cells can show relatively good agreement with Mie theory [10], allowing application to a variety of biological scatterers.
A more sophisticated approach to modeling scattering is to use the T-matrix method, also referred to as the extended boundary condition method (EBCM), a generalization of Mie theory to arbitrarily shaped objects that reduces to Mie theory in the spherical case [11]. Because most cell nuclei are approximately spheroidal rather than spherical, the T-matrix is a more widely applicable alternative to Mie theory that can provide more accurate solutions. Furthermore, the T-matrix method enables simulation of the effects of parameters beyond the size and refractive index of cell nuclei, including the extent to which scatterers are elongated (aspect ratio) and the orientation of scatterers [12, 13].
Unfortunately, generating comprehensive databases of T-matrix solutions is computationally challenging, both because nonspherical solutions are more computationally complex and because the range of biologically interesting geometries is much larger than in Mie theory [14]. This disadvantage is partially offset by the availability of very efficient FORTRAN codes that implement recent advances in T-matrix modeling [15].
Experimentally, detection of angular ESS signals has been demonstrated with Fourier plane imaging. In this approach, the detection element is located in a Fourier transform conjugate plane [16] to the scattering sample such that the spatial distribution of light in the Fourier plane corresponds to light scattered at a particular angle by the sample. Thus, a spatially selective detection scheme such as an aperture can be used to detect light scattered over a range of angles. In one implementation of an angular ESS scheme, the input slit of an imaging spectrograph was placed in a Fourier plane of scattering samples, enabling both spectral and angular scattering to be observed simultaneously [17]. This approach, termed elastic light-scattering fingerprinting, was used to study early carcinogenesis events in ex vivo rat colon [18]. In another implementation, angular ESS information has been obtained using Fourier plane imaging in a microscopy scheme [19]. This method has been applied to study scattering changes associated with apoptosis [20]. A third approach uses holographic methods to record angular scattering due to localized particles [21]. These approaches offer the advantages that scattering data are collected in parallel rather than serially; they are compatible with broadband light sources and permit detection of light scattered near the backscattering direction which is important for probing the structure of larger structures, such as cell nuclei.
38.3 Angle-Resolved Low-Coherence Interferometry: Combining ESS and OCT for Detecting Precancerous Cells
Angle-resolved low-coherence interferometry (a/LCI) has been developed as an angular ESS method for probing the structure and organization of cells and their components. The a/LCI technique is unique among angular ESS approaches in that it uses coherence gating, the mechanism employed in optical coherence tomography (OCT) to achieve depth resolution, in order to isolate the component of returned light due to single scattered photons. While a/LCI and OCT share the ability to selectively probe subsurface layers, conventional OCT implementations lack the resolution and contrast to quantitatively assess changes in subcellular features. In contrast, because a/LCI uses elastic scattering spectroscopy to assess structure, it can detect changes in subcellular structure. Early efforts to combine the ESS and OCT methods sought to perform a/LCI using a Michelson interferometer [9, 22, 23] to measure depth-resolved scattered fields as a function of scattering angle. In a/LCI, the transverse component of the momentum transfer associated with the light-scattering process is detected by using Fourier plane imaging concepts with interferometry where the reference field is tailored to select specific transverse momenta, i.e., angles of propagation for detection. This section presents the optical design and evolution of a/LCI schemes and the theoretical basis which permits structural information to be extracted from the scattering distributions.
38.3.1 Optical Design of a/LCI Systems
There have been three implementations of a/LCI systems for detecting the angle-resolved scattering distribution using low-coherence interferometry. These include the Michelson interferometer-based a/LCI prototype; a second-generation a/LCI system based on a Mach–Zehnder interferometer, which records depth-resolved data in the time domain; and, the most recent, clinical a/LCI implementation based on spectral-domain interferometry. The primary driving force behind the evolution of a/LCI systems has been to improve the speed of data acquisition while also providing low-noise, high-fidelity measurements, to enable clinical application to detecting dysplasia in human epithelial tissues based on measuring the size of cell nuclei.
The first a/LCI systems used time-domain interferometry in Michelson geometry similar to time-domain OCT. Depth scanning was accomplished by translating the sample [23] or reference [22] arms, while measurement of the angular distribution was accomplished by translating a lens perpendicular to the beam pass to scan the angular distribution across a photodiode. However, this approach suffered from limited sensitivity due to the use of a kHz Doppler shift to separate the interferometric signal from the DC background. Combined with the very low intensity per angle of typical scattered fields, these systems required long scan times of greater than 30 min to acquire sufficiently high sensitivity measurements.
Following the demonstration of time-domain a/LCI, an improved implementation based on a Mach–Zehnder interferometer (MZI) was developed to address these limitations [24, 25]. The MZI implementation improved sensitivity by separating the collection optics from the angle scanning optics and introducing acousto-optic modulators with balanced heterodyne detection. The resulting system demonstrated higher angular resolution and sensitivity combined with faster scan times of less than 5 min and enabled a number cellular [26] and ex vivo tissue studies [27].
Recent advances in OCT have shown that improvements in signal-to-noise and reductions in data acquisition time are possible by recording the depth scan in the Fourier (or spectral) domain [28–30]. These advances were leveraged to implement Fourier-domain a/LCI [31]. In this approach, measurement is again performed using a Mach–Zehnder interferometer, but the reference arm is fixed and a spectrometer is used to read out a spectral interferogram as in Fourier-domain OCT. Furthermore, by using an imaging spectrometer, angle scanning optics are obviated by rapid parallel detection along the spatial channel of the spectrometer.
By combining the Fourier-domain a/LCI scheme with a coherent fiber bundle, angle-resolved measurements can be performed endoscopically, enabling in vivo applications. Figure 38.1a depicts an endoscopic a/LCI system using a coherent fiber bundle [32]. The system again consists of a Mach–Zehnder interferometer, now implemented using fiber-optic components to minimize space. Light from a superluminescent diode (SLD) is divided into a sample (90 %) and reference (10 %) arms by a fiber splitter (FS). The sample arm light is delivered by a polarization-maintaining delivery fiber (DF) and grin lens L1 onto the sample (Fig. 38.1b). The use of a separate delivery fiber is essential because it ensures the illumination angle and polarization state are precisely controlled, an essential feature for accurately determining cell morphology [33].
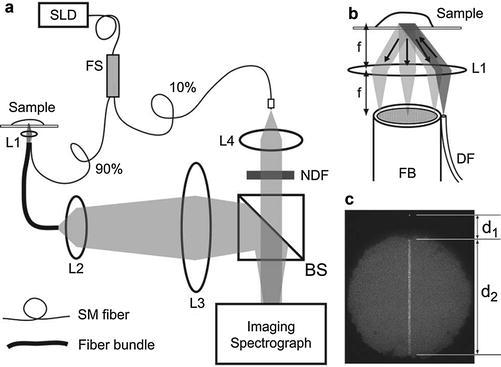

Fig. 38.1
Fiber-based Fourier-domain a/LCI system taken from [32]. (a) Diagram of the endoscopic interferometer. (b) Detailed view of the sample optics. (c) Photograph of the fiber bundle face
Light scattered from the tissue surface is collected by lens L1 and relayed to the distal face of the fiber bundle. By positioning the face of the fiber bundle in the Fourier plane of L1, each channel of the bundle receives light scattered at a particular angle. The light relayed by the bundle is imaged onto the entrance slit of an imaging spectrometer along with the overlapped reference field. The imaging spectrometer slit is positioned along the center of the fiber bundle (Fig. 38.1c) with approximately 130 fibers imaged onto the slit in order to capture a comparable angular range as used in previous a/LCI systems. By carefully determining the magnification so that individual fibers are adequately sampled, cross talk between adjacent angular channels can be minimized. Although the fibers are not single mode, coherence gating effectively rejects any contribution from higher-order modes which experience a much greater optical path length [34].
An alternative collection method to using a coherent fiber bundle is to use a single-mode optical fiber combined with mechanical scanning to obtain scattering measurements. This approach was implemented in the fiber-optic interferometric two-dimensional scattering (FITS) system to perform polarization-resolved one- or two-dimensional scattering measurements by translating a single-mode fiber across the back focal plane of a collection lens [35]. Polarization selectivity is obtained using a novel hybrid Michelson–Sagnac hybrid interferometer implemented in fiber. By mixing the scattered field and reference field inside of an optical fiber, the polarization state of the detected field can be precisely measured. Furthermore, as the reference and sample arms propagate along common single-mode fibers, the system is relatively insensitive to dispersion, even in very long fiber probes. Although the FITS system forgoes the sensitivity advantage of parallel detection, it was the first a/LCI system capable of 2D measurement of scattered fields.
38.3.2 Processing a/LCI Distributions to Obtain Structural Information
As discussed above, a/LCI signals must be processed and then analyzed in order to determine structural features from measurements of angle-resolved scattering. In frequency-domain a/LCI, light at each scattering angle is detected as a function of wavelength such that the detected signal can be related to the signal and reference fields (Es, Er) by [36]

where ϕ is the phase difference between the two fields, the indices (m, n) correspond to a particular pixel, and 〈〉 denotes a temporal average.

(38.2)
In order to process the raw pixel data to produce depth-resolved scattering measurements, the data are processed as described in [37], in a process similar to Fourier-domain processing of OCT signals. First, the average intensities of the sample and reference beams are measured independently and then subtracted from I. Second, at each scattering angle, the spectrum in wavelength (λ) is converted into a linear function of wavenumber (using k = 2π/λ), using a cubic spline interpolation. At this point, any chromatic dispersion in the system is corrected numerically using empirical parameters. Finally, at each scattering angle, the spectrum as a function of wavenumber is 1D Fourier transformed to generate a signal which is a function of optical path length (or depth in the sample).
This processed signal is analyzed to determine structural information, typically the size of cell nuclei in a tissue sample. First, the angular distribution is divided by the normalized reference field, which varies smoothly from 0.5 to 1, to produce a signal that is linear in the scattered field. The scaled data are then squared to yield scattered intensity versus angle and path length. These data are further processed to remove high-frequency noise by binning the angular data. The angular data for a particular depth (optical path length) are then compared to database of theoretical predictions which have been calculated previously. Chi-squared values are calculated as the mean square difference between the data and each theoretical prediction for a range of scatterer diameters. The minimum chi-squared value is determined by searching through all values generated and the corresponding size is reported as the best fit. The uncertainty in these measurements is given as the change in structure diameters where the minimum chi-squared value is doubled.
Although this procedure is generally applicable, additional steps must be taken for the specific case of analyzing scattering due to cell nuclei. As discussed in detail in [33], accurate size determination can be complicated by other structures if the angular data are compared directly to the predictions of Mie theory. First, one must consider that Mie theory predicts scattering by a homogenous dielectric sphere while, for most cells, the nucleus is not a sphere but rather a spheroid. In addition, the presence of inhomogeneities in and around the nucleus can also complicate interpretation of the angular-scattering distribution.
The a/LCI analysis algorithm for extracting nuclear size information from cells and tissues consists of four steps. First, data from a particular region of interest are selected, usually corresponding to a particular tissue layer. The data are then filtered to remove high-frequency oscillations, as described above. Since the angular distribution is Fourier transform related to the two-point correlation function (Eq. 38.1), removing these oscillations over fine angular scales corresponds to suppressing scattering arising from long correlation distances. Physically, this step removes the contribution to angular scattering arising from coherent scattering by neighboring cell nuclei which are necessarily spaced at distances greater than the cell size. This effect was examined in a previous study [38] which systematically varied cell spacing to demonstrate that this process permitted accurate size determinations in the presence of coherent scattering by adjacent cell nuclei. An additional filtering step is then implemented, which uses a second-order polynomial to remove the background trend from the processed data. This step is important to enable fitting using chi-squared minimization and serves to isolate the oscillatory component of the angular scattering due to diffraction, as described in [39]. The final step of the analysis is to compare the processed angular distribution to theoretical distributions which have also had their background trend removed. For determining the size of cell nuclei, a database of calculated distributions will include a Gaussian distribution of scatterer sizes, characterized by a mean diameter (d) and a standard deviation (δd) in the size parameter, a range of refractive indices of the nuclei (nnucleus), and a range of refractive indices of the cytoplasm (ncytoplasm).
As a final note, when fitting data for cell nuclei, whether in isolated cells or from tissue, criteria that establish a unique fit are needed. The a/LCI processing typically employs two checks, including a comparison with scattering that is constant versus angle and demanding that the chi-squared value for the best fit is at least 10 % greater than the next best value to ensure a unique fit.
Processing of a/LCI data can be readily generalized to two-dimensional, solid angle-resolved fields resulting in more accurate measurement of size and shape. In this case, the database of theoretical scattering solutions is constructed with scattered field intensities recorded over two dimensions. The scattering simulations and the 2D measurement coordinates are coregistered by comparing measurements from known scattering samples to the simulated values. During this step, effects such as field curvature can be removed if present. After coregistration, low-pass filtering is implemented similar to the 1D process by using a 2D filter kernel and second-order polynomial subtraction. The processed measurement data is then compared on an angle per angle basis to generate a χ 2 error value for each database entry. As in the 1D case, the simulation with the lowest χ 2 value indicates the scattering geometry.
38.4 Applications of a/LCI
A number of studies have employed a/LCI to investigate structure through depth-resolved angular-scattering measurements. These include validation experiments with polystyrene microspheres and in vitro cells which have served to demonstrate various aspects and capabilities of the technique. Further experiments have applied a/LCI to examine the nuclear morphology of epithelial cells in tissues drawn from animal models of carcinogenesis. Finally, a clinical implementation of a/LCI has been developed which introduces an endoscopic fiber-optic probe that is compatible with standard endoscopes. This section concludes with ex vivo and in vivo studies which apply the new fiber probe to detect precancerous changes in human epithelial tissues.
38.4.1 a/LCI Validation Experiments
Validation of the a/LCI approach was first achieved by measuring the scattering distribution of polystyrene microspheres [22]. Upon realizing Fourier-domain a/LCI, it became much easier to acquire scattering data and a study was undertaken to demonstrate the capability of the system across a range of clinically relevant-sized polystyrene microspheres of sizes 6.0, 8.0, 9.7, 12.0, and 15.0 μm [37]. The results showed that a/LCI-determined mean diameter agreed very well with the corresponding NIST traceable mean diameters, producing an r2 value of 0.9997.
While polystyrene microspheres are suitable targets for developing light-scattering systems, measurement of cell nuclear morphology is a more challenging target due to the lower refractive index compared to the surrounding medium. The first application of a/LCI to measurement of nuclear morphology was accomplished using monolayers of cultured HT29 epithelial cells [9], a line of human tumor cells. This study demonstrated sub-wavelength precision and accuracy by comparing the light-scattering results to quantitative image analysis (QIA). This first application also developed the signal-processing methods to account for the nonspherical and inhomogeneous nature of cell nuclei. Significantly, this work identified a power law correlation function that described the residual light-scattering signal once the nuclear contribution was removed. A more comprehensive study of scattering by in vitro cells was completed by Pyhtila et al. [33], which explored the role of polarization in analyzing light-scattering signals from cell nuclei. A comprehensive list of a/LCI nuclear morphology data for in vitro cells can be found in Biomedical Applications of Light Scattering [40].
The first use of the T-matrix method for assessing the size of cell nuclei using with a/LCI was demonstrated using cultured MCF-7 breast cancer cells [12]. In these experiments, 37 a/LCI measurements were taken with 48 angles per measurement from six cell monolayers prepared on coverslips. Cells were then imaged using DAPI fluorescence and QIA to determine nuclear diameter. Analysis was enabled by a T-matrix database that contained simulated scattering for nuclei from 7.5 to 12.5 μ diameter in increments of 40 nm, spheroidal aspect ratio from 0.56 to 1 (prolate to spherical) in increments of 0.01, background index of refraction 1.35 and 1.36, and scatterer index of refraction 1.42 and 1.43, all with a 10 % standard deviation normal size distribution. Both methods provided nearly identical answers, with QIA yielding an EVD of 9.52 μm (95 % standard error = 0.44 μm) and an aspect ratio of 0.70 ± 0.026 and a/LCI with T-matrix determining an EVD of 9.51 ± 0.34 μm with an aspect ratio of 0.69 ± 0.032 determined. These results confirmed the ability of a/LCI to measure both the size and shape of living cell nuclei with extremely high accuracy.
Following the demonstration of T-matrix-based analysis in a/LCI, the technique was generalized to 2D using and the FITS system to analyze scattering from stretched polystyrene microspheres [41]. In these experiments, small numbers of microspheres were mixed into transparent plastic, heated beyond their melting point, and then allowed to cool under tension. The resulting phantoms had a nearly perfect spheroidal geometry of known size and shape. A database was prepared using the T-matrix method to simulate the complex polarization state of the 2D angle-resolved fields over 360° of azimuth angle and 30° of polar angle (corresponding to the range achieved in 1D a/LCI). In total, 10,250 unique scatterer geometries were simulated with equal volume diameters ranging from 8 to 18 μm in 80 nm increments and aspect ratios between 0.7 (prolate spheroidal) and 1.1 (oblate spheroidal) in steps of 0.005 [42].
Individual stretched microspheres were selected and scanned using the FITS system and then analyzed using a T-matrix database. Measurements were presented for three representative samples of microspheres with a diameter of 15.02 μm +/− 80 nm prior to stretching [43]. In the spherical geometry, a/LCI measured an equal volume diameter (EVD) of 15.00 ± 0.24 μm and an aspect ratio of 0.995 ± 0.04. For a slightly stretched (QIA aspect ratio = 0.93) spheroid, a/LCI measured an EVD of 14.95 ± 0.33 μm and an aspect ratio of 0.925 ± 0.01. Finally, for a moderately stretched (QIA aspect ratio = 0.82) spheroid, an a/LCI measured an EVD of 15.00 ± 0.24 μm and an aspect ratio of 0.825 ± 0.005 (Fig. 38.2). This analysis demonstrated that 2D a/LCI size and shape determinations are unique even over very large parameter spaces.
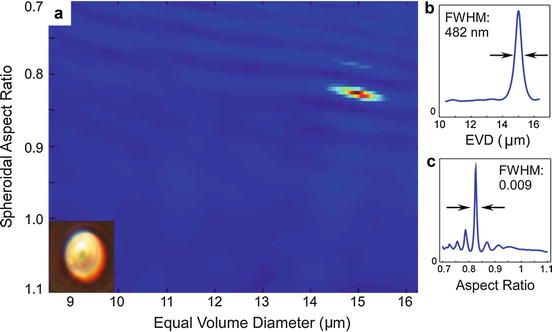

Fig. 38.2
(a) χ 2 error plotted against equal volume diameter and aspect ratio for a single 0.82 (determined by QIA) 15 μm stretched microsphere (see inset). (b) Plot of χ 2 compared to diameter. (c) χ 2 error compared to aspect ratio (Adapted from [41])
38.4.2 Application of a/LCI in Cell Biology
The ability of a/LCI to noninvasively measure changes in cell nuclei with wavelength accuracy has been applied to measurement of cell dynamics in several experiments. In the first of these, subtle changes in the volume of cell nuclei with changes in osmolarity were measured with Mie theory [44]. This study also showed that changes in cell nucleus shape due to a substrate texture could be measured with a/LCI but required multiple measurements with different orientations of the sample. With the development of T-matrix-based fitting for the measurement of both size and shape, a/LCI was extended to measure deformation of cell nuclei in response to nanopatterned substrates within a single measurement [13]. These results demonstrated that real-time quantitative measurement of changes in live cells in response to environmental stimuli was possible without the use of exogenous contrast agents.
The improved accuracy enabled by T-matrix-based fitting was subsequently used to investigate the onset of apoptosis in breast cancer [45]. In these experiments, cells were treated with one of two chemotherapeutic agents at levels sufficient to initiate apoptosis. Treated cells were then measured at regular intervals with a/LCI and the size and shape determined with T-matrix-based processing. The T-matrix fit was then subtracted from the angular-scattering data and Fourier transformed to obtain a residual signal correlation function. While the size and shape data did not appreciably change due to treatment, analysis of the residual signal using a fractal dimension formalism did produce statistically significant results, showing a dramatic change 3 h after treatment with paclitaxel (Fig. 38.3a) and doxorubicin (Fig. 38.3b). Subsequently, time courses demonstrated a statistically significant change after just 90 min (Fig. 38.3c), demonstrating that angle-resolved light scattering can detect pre-apoptotic changes in nuclear organization.
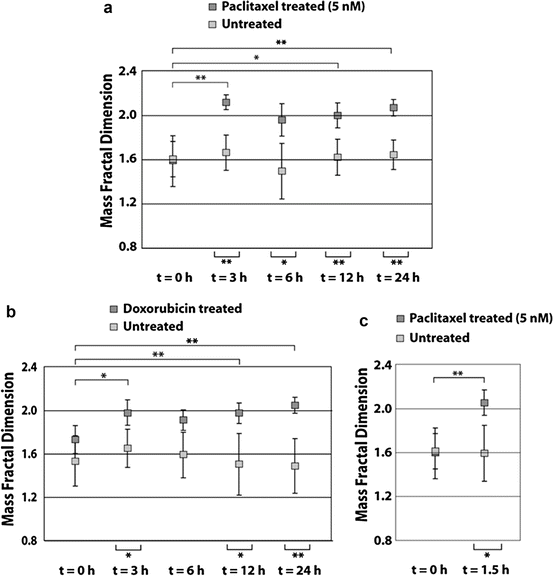

Fig. 38.3
a/LCI T-matrix-measured fractal dimension of chemotherapy-treated cells. (a) Fractal dimension after 0, 3, 6, 12, and 24 h after paclitaxel treatment demonstrating a rapid increase in fractal dimension following the initiation of apoptosis. (b) Previous results repeated for doxorubicin. (c) Paclitaxel treatment after 90 min (Taken from [45])
38.4.3 Application of a/LCI to Detecting Precancerous Lesions in Animal Tissues
The first application of a/LCI to assessing structure within tissues was in quantitative studies of the nuclear morphometry of epithelial cells in a rat model of esophageal carcinogenesis [46, 47]. Changes in the size and texture of cell nuclei due to neoplastic transformation were observed in situ via quantitative measurements of basal epithelial cell nuclei, approximately 50–100 μm beneath the tissue surface. In the first study, a/LCI measurements, made on freshly excised tissue samples without using exogenous contrast agents or tissue fixation, were compared to traditional histopathological images to establish a correlation with the degree of neoplastic transformation [47]. The grading criteria from this initial study were then used to detect neoplastic transformation in a prospective study [46].
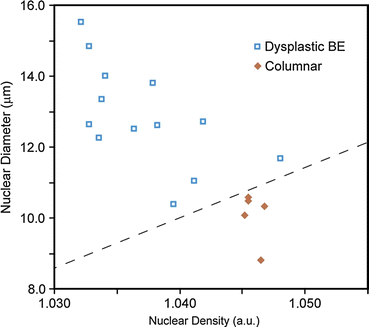
The rat esophagus studies focus on two morphological parameters: the mean nuclear size and the fractal dimension. The a/LCI measurements of these parameters from the first study are presented graphically in Fig. 38.4. The measurements are grouped by histological classification: normal epithelium, low-grade dysplasia (LGD), high-grade dysplasia (HGD), epithelium with vacuolated cells, or epithelium with apoptotic cells. The latter two classifications were seen in tissues treated with prospective chemopreventive agents. The observations of vacuolization and apoptosis using a/LCI are important findings as it illustrates a potential application of the technique for assessing the efficacy of chemopreventive agents or the toxic effects of chemicals on tissue health.
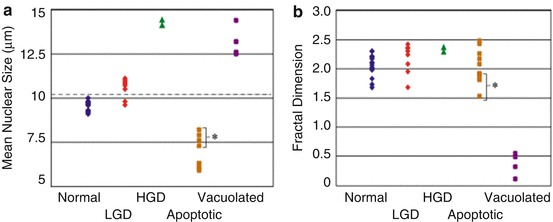

Fig. 38.4
(a) Average cell nuclei size from intact excised rat esophagus tissues as determined with a/LCI. The dashed line represents a decision line between normal and dysplastic cells. (b) Fractal dimensions of subcellular components measured using a/LCI. There is a significant difference (p < 0.05) between normal and dysplastic (LGD+HGD) populations (From Ref [47])
In this first study [47], the mean nuclear size was found to be a powerful indicator of neoplastic progression, resulting in 80 % sensitivity and 100 % specificity in distinguishing normal from dysplastic tissues. In addition, apoptotic cells could be easily distinguished via nuclear size distribution. The fractal dimension measurements did not improve the diagnostic capability of a/LCI for classifying neoplasia, but fractal dimension measurements were later found to offer utility in assessing therapy [45].
In a second prospective study of the rat esophagus carcinogenesis model [46], the tissue classifications established in the initial study were used to grade tissue samples. Freshly excised esophageal tissues were examined using a/LCI at time points of 8, 12, and 20 weeks following treatment with N-nitrosomethylbenzylamine (NMBA). The degree of neoplastic transformation was assessed by measuring the average diameter of the cell nuclei in the basal layer and comparing to the grading criteria established previously. This prospective study showed that a/LCI successfully identified 58 of 60 normal tissue sites (97 % specificity) and 20 of 22 dysplastic tissue sites (91 % sensitivity) upon comparison to traditional histopathology. In addition, this study further reinforced the use of a/LCI for assessing the efficacy of chemopreventive agents, by comparing the modulation in incidence of neoplastic change due to addition of difluoromethylornithine (DFMO) to the diet of the animals. The a/LCI data showed no difference in incidence at 8 weeks but that DFMO was effective in reducing the incidence of dysplasia at 12 and 20 weeks post-NMBA treatment. Traditional tumor metrology measurements confirmed the observation of modulation in incidence at 20 weeks but could not detect it at earlier times, suggesting that a/LCI can provide greater sensitivity than traditional methods.
38.4.4 Application of a/LCI to Human Tissues
The first demonstration of the clinical utility of a/LCI was shown with measurements on ex vivo human tissue samples from three patients with dysplastic Barrett’s esophagus (BE) who underwent esophagogastrectomies [48]. The tissue was opened longitudinally and data was taken within 2 h of resection. These studies showed a high sensitivity and specificity for distinguishing dysplastic BE tissue from healthy columnar tissue (Fig. 38.5), as would be found in the gastric epithelium. No non-dysplastic BE tissue was encountered. A follow-up study was conducted using the first portable a/LCI system in the pathology clinic, enabling data to be taken within 1 h of resection [36]. This study employed a handheld optical probe, allowing precise selection of the location for each data point and enabling better coregistration. Three types of tissue from a single specimen were probed. Data were acquired from normal squamous tissue from the esophagus, from the normal-appearing gastric tissue from the stomach, and from Barrett’s tissue in the esophagus which appeared normal but was later classified as low-grade dysplasia in the pathology report. As with the previous ex vivo study, no non-dysplastic BE tissue was observed. These data showed good sensitivity (100 %; 6/6) for the superficial 150 μm of the epithelium using a similar decision line used in the previous study; however, the specificity was lower (56 %; 5/9). When the analysis was extended to include a deeper segment of tissue, which contained the basal layer, there was again excellent sensitivity (100 %; 6/6) but also improved specificity (78 %; 7/9). This result indicated that the deep basal layer might provide the greatest insight into the disease state of the tissue as measured by a/LCI.