(43.1)
where Δf(x, y, z) is the mean Doppler frequency shift between time t and t+τ and at a sample location of x (fast scan direction), y (slow scan direction), and z (depth). Γ1(x, y, z, t) and Γ2(x + Δx, y, z, t + τ) are the complex OCT signals of the first and second A-lines. Δx is the spatial displacement between the two A-lines and is now assumed to be negligibly small in comparison to the transversal resolution of OCT. The subscript of * indicates a complex conjugate.
The Doppler frequency shift Δf(x, y, z, t); Doppler phase shift Δφ(x, y, z, t), i.e. the phase difference between the two A-lines Arg[Γ1(x, y, z, t)Γ2*(x + Δx, y, z, t + τ)]; and the sample velocity are related as
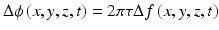
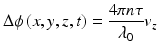
where n is the refractive index of the sample, λ 0 is the center wavelength of the probe beam, and v z = v cos θ is the axial component of the velocity of the sample with the sample velocity of v and the angle between the probe beam and the direction of the motion θ. Equation 43.2 indicates that, even with a same velocity, the Doppler phase shift Δφ(x, y, z) becomes larger with a lager τ. Hence, a larger τ provides a better signal-to-noise ratio for Doppler phase detection and consequent higher Doppler sensitivity when the phase noise of the OCT is constant in respect to τ.
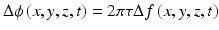
(43.2)
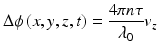
(43.3)
However, in standard OCT implementation, the phase noise is not constant in τ. In the discussions above, we have assumed the spatial separation of two A-lines, Δx, is negligibly small. Meanwhile, in standard Doppler OCT, Δx and τ are related as Δx = v s τ with v s of the transversal scanning velocity of a probe spot on the sample. Hence, the assumption of a small Δx is no longer valid with a large τ. The larger Δx is known to increase the phase noise [39, 40]. As a result, a large τ enhances the Doppler phase shift but also increases the phase noise.
This property of Doppler OCT suggests that a possible Doppler OCT system that enables a large τ with a small Δx would be an ideal system to provide high Doppler sensitivity. DB-OCA described in this chapter is an extension of Doppler OCT, which provides this condition and hence enables very high Doppler sensitivity.
43.2.2 Principle of Dual-Beam Doppler Optical Coherence Tomography
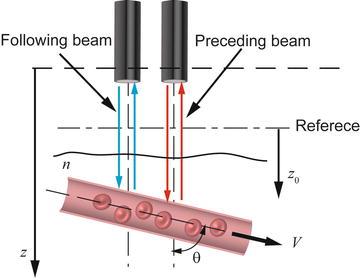
DB-OCA utilizes a Doppler detection scheme measuring the single Doppler frequency shift from two backscattered lights associated with two probe beams. The two probe beams have the same scanning speed and are spatially separated on the sample in the scanning direction as depicted in Fig. 43.1. Through the scanning of probes over the sample, the electric fields of lights, E p (x, y, z, t p ) and E f (x, y, z, t f ), are backscattered from a position (x, y, z) in the sample and are collected at different times, t p and t f , where the subscripts of p and f denote preceding and following probes, respectively. Spectrally resolved interference signals between collected lights and the reference light are detected and Fourier transformed into complex OCT signals, Γ p (x, y, z, t p ) and Γ f (x, y, z, t f ) [23]. Since the motion of the sample causes a Doppler frequency shift Δf(x, y, z), it modulates the complex OCT signals as
![$$ {\Gamma}_p\left(x,y,z,{t}_p\right)={\Gamma}_p^{\prime}\left(x,y,z\right) \exp \left[i2\pi \Delta f\left(x,y,z\right){t}_p\right] $$](/wp-content/uploads/2017/03/A76297_2_En_44_Chapter_Equ4.gif)
![$$ {\Gamma}_f\left(x,y,z,{t}_f\right)={\Gamma}_f^{\prime}\left(x,y,z\right) \exp \left[i\;2\pi\;\Delta f\left(x,y,z\right)\;{t}_f\right] $$](/wp-content/uploads/2017/03/A76297_2_En_44_Chapter_Equ5.gif)
where Γ f ′(x, y, z) and Γ f ′(x, y, z) are the time-independent components of the preceding and following probes, respectively. Using the same wavelength for the two probes, we can assume Γ f ′(x, y, z) = Γ f ′(x, y, z). Under this circumstance, the Doppler frequency shift is obtained by calculating the phase difference between Γ p (x, y, z, t p ) and Γ f (x, y, z, t f ) as
![$$ \Delta f\left(x,y,z\right)=\frac{1}{2\pi \tau}\mathrm{A}\mathrm{r}\mathrm{g}\left[{\Gamma}_p\left(x,y,z,{t}_p\right){\Gamma}_f^{*}\left(x,y,z,{t}_f\right)\right] $$](/wp-content/uploads/2017/03/A76297_2_En_44_Chapter_Equ6.gif)
where the time interval τ ≡ t f − t p . When the spatial separation of the two probes on the sample is d and the scan speed of the probe is v s , τ is configured to be τ = d/v s . Since d can be arbitrarily configured using a proper optical design, τ can also be arbitrarily selected. By selecting a large τ, as suggested by Eq. 43.3, we can enlarge the Doppler phase shift value. In addition, two OCT signals utilized in the Doppler calculation in Eq. 43.6 were obtained at the same location in the sample. Namely, Δx that appears in the standard Doppler OCT equation (Eq. 43.1) becomes zero. Hence, phase noise elevation with a large Δx does not occur. Due to these properties, DB-OCA enables extremely high-sensitive Doppler OCT detection.
(43.4)
(43.5)
(43.6)
Fig. 43.1
The detection scheme of DB-OCA
43.2.3 Implementation of Dual-Beam Doppler OCA
DB-OCA can be implemented by several means including Wollaston prism-based polarization multiplexing [34], polarization multiplexing with a polarization beam splitter [38], and an interferometer multiplexing method [35]. In this section, we describe the Wollaston-based polarization multiplexing method as the simplest examples. Some of the other implementations and extensions of DB-OCA are described in a later section.
43.2.3.1 Hardware Implementation
The instrumentation diagram of DB-OCA is presented in Fig. 43.2. In this setup, two probing beams are multiplexed in two orthogonal polarization states. The light source is a superluminescent diode (SLD-37-HP, Superlum Diodes Ltd., Ireland, in this example) with a center wavelength of 840 nm and spectral bandwidth of 50 nm (full width at half-maximum: FWHM). The beam from the light source propagates in a single-mode (SM) fiber and passes through an isolator and then a polarization controller. The light is split into the fast and slow modes in the polarization-maintaining (PM) fiber. The interferometer consists of a PM fiber coupler. In this particular example, the splitting ratio of the coupler is 80/20 with 20 % going to the sample arm.
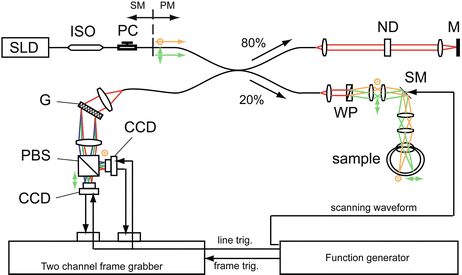
Fig. 43.2
Instrumentation scheme of DB-OCA based on spectral domain optical coherence tomography uses a superluminescent diode (SLD). Orthogonal polarization states are separated and independently propagated inside a polarization-maintaining (PM) fiber 80/20 coupler. They are separated spatially on the sample using a Wollaston prism (WP) and scanned by a scanning mirror module (SM). Reference beams are attenuated by a neutral density filter (ND) and reflected by a mirror (M). The reference arm should exhibit no birefringence to avoid crosstalk between the two channels. Interference signals of each polarization state are detected by a polarization-sensitive spectrometer consisting of a grating (G), polarization beam splitter (PBS), and two-line scan CCD cameras (CCD). The cameras are synchronously driven by the same trigger from a function generator through a frame grabber
Two polarization modes are separated by a Wollaston prism in the probing arm. The separation angle of the Wollaston prism is 0.35°. Two polarization modes independently propagate in the system. The separation of two modes on the cornea becomes 0.684°. After passing the eye optics, the two polarization modes form two probe light spots on the retina and are backscattered. The backscattered lights are combined again by the Wollaston prism and introduced to a polarization-sensitive spectrometer through a PM fiber. The two backscattered lights from the sample are independently detected by a polarization-sensitive spectrometer [41]. In this spectrometer, a polarization beam splitter divides the two polarization modes, and two-line scan cameras (AViiVA M2 CL 2014, e2V) detect each mode. The acquisition rate of the camera is 27, 778 lines/s.
The polarization controller in the SM fiber regulates the polarization state at the connection between the SM and PM fibers to ensure identical optical powers in each mode and the same sensitivity in both polarization channels. The optical power on a sample is 370 μW for each polarization mode. The total power is 740 μW, which is lower than the safe exposure limit according to the ANSI standard (Z136.1) [42].
In this particular example, the predicted shot-noise-limited sensitivity is 100 dB with an integration time of 34.8 μs. The sensitivity was measured as 94 dB and 93 dB for each channel, which was approximately 6 dB lower than the shot-noise-limited sensitivity. This is reasonable since the optical power loss of the system was measured as 6.5 dB, which may be due to the loss at fiber re-coupling, polarization crosstalk in optical components, and the alignment error of the mirror sample for sensitivity measurement because of the difficulty in aligning the mirror for both separated sampling beams. The beam diameter at 1/e 2 on the cornea is about 820 μm. The beam spot diameter on the retina is around 13 μm (FWHM). The axial resolution of approximately 8 μm (FWHM) in air is achieved.
43.2.3.2 Processing of Flow Signal
In the signal processing procedure, the two OCT signals obtained by the preceding and following probes are accurately co-registered and aligned to each other. The lateral alignment is performed by accounting the time interval between the two probe beams. A fiber length mismatch between the sample and reference arms and the resulting group delay mismatch between the two polarization channels of the PM fiber cause axial displacement between the two OCT signals. The variance of the phase difference of two OCT signals, which takes its minimum when the axial displacement is canceled, is utilized for the axial alignment. The axial displacement was determined during the system calibration process by minimizing the phase variance of OCT signals obtained from a static turbid phantom. The axial displacement of two OCT images of a real sample, e.g., a retina, is then numerically canceled according to this predefined amount of axial displacement.
After the alignment process, the Doppler phase shift between these two OCT images is obtained using the Kasai autocorrelation with complex averaging as
![$$ \Delta \phi \left({x}_i,{z}_j\right)=\mathrm{A}\mathrm{r}\mathrm{g}\left[{\displaystyle \sum_{k=1}^M{\displaystyle \sum_{l=1}^N{\Gamma}_f\left({x}_{i+k+m},{z}_{j+l}\right)}}{\Gamma}_p^{*}\left({x}_{i+k},{z}_{j+l}\right)\right] $$](/wp-content/uploads/2017/03/A76297_2_En_44_Chapter_Equ7.gif)
where Γ p and Γ f are complex OCT signals obtained with the preceding and following probes, respectively. i and j are lateral and axial indices of pixels, m is the number of axial scans acquired in the time interval between the two probes τ, and M and N are lateral and axial window sizes, respectively.
(43.7)
43.2.3.3 Image Processing for Angiographic Visualization
One important post-image process to generate an OCA image is removing the low signal region. Since the low signal-to-noise ratio exhibits a random phase distribution, it disturbs flow images and significantly degrades the clinical utility of OCA.
In order to enhance the signal-to-noise ratio of OCA, the Doppler phase shift at the pixels that have lower average autocorrelation amplitudes g(x i , z j ) is masked out and set to zero, where g(x i , z j ) is defined as
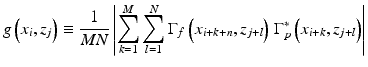
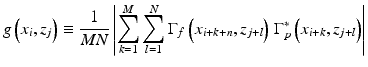
(43.8)
In the random noise region, the complex signals at the pixels in the averaging window cancel each other, and g(x i , z j ) approaches zero. On the other hand, in the region with significant signal strength, g(x i , z j ) takes a relatively large value. Hence, by applying a low threshold value, the noise region and signal region are effectively classified.
As for additive white noise, SD-OCT noise is a zero-mean circular Gaussian variable in a complex plane. On the other hand, its amplitude is no longer a Gaussian variable but a random Rayleigh variable. In contrast, Eq. 43.8 contains an amplitude of product of an OCT signal and the complex conjugate of another OCT signal, and hence its noise distribution becomes a double-Rayleigh distribution [43]. According to the statistical property of OCT amplitude, the mean and standard deviation of the amplitude of the auto-correlation at the noise region are μ a = πσ 2/4 and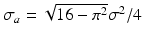 
, respectively, where σ is the standard deviation of amplitude noise in the OCT signal. Using μ a and σ a , the pixels to be masked are determined as:
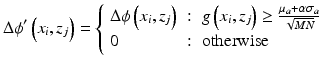
where α is a constant factor and set as 4 or 6 in for the cases described in Sect. 43.3.
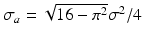, respectively, where σ is the standard deviation of amplitude noise in the OCT signal. Using μ a and σ a , the pixels to be masked are determined as: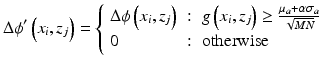(43.9)
A squared Doppler phase shift is calculated from the result of Eq. 43.9 and is used for qualitative vasculature imaging. Projection images, i.e., en face OCA, are created by integrating the squared phase shift along the depth. By applying a retinal layer segmentation algorithm [32], two en face OCAs are created for the retina and the choroid. Stereograms, which are pairs of projections from slightly different angles, also can be created to provide a three-dimensional distribution of the vasculature.
43.3 Application to the Human Eye In Vivo
In this section, the clinical utility of DB-OCA is demonstrated by imaging normal pathologic cases. DB-OCA was used to investigate the retina and choroid in three dimensions with a resolution of approximately 15 × 30 × 6 μm (horizontal sampling separation × vertical sampling separation × and coherence length).
43.3.1 Capillary Imaging
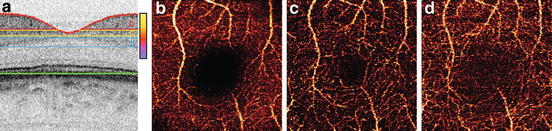
To demonstrate the capability of DB-OCA for fine capillary imaging, juxtafoveal regions of normal eyes without marked posterior disorder were investigated. The eyes of three healthy subjects were scanned over a 1.9 × 1.9 mm2 area with 512 × 256 points. A relatively slow transversal scanning speed was selected to enable a very long time interval between the preceding and following probes of τ = 1.58 ms.
Retinal capillaries around the fovea were visualized in three dimensions with a stereogram. The three-dimensional complex and dense capillary network of the macula is shown in Fig. 43.4a. A volume rendering [44] with a depth-encoded color map (Fig. 43.4b) shows that retinal capillaries comprise roughly three layers (yellow, orange, and purple vessels). The depth-segmented projections (Fig. 43.3) show different patterns of the retinal capillary network at each depth. These appearances are consistent with histological findings [45]. The relatively thick retinal vessels at the anterior retina appeared through all depth segments, which may because of the shadowing effect of Doppler OCT [18].
