, Gesa Franke2, 3, Christian Lührs1, Peter Koch2, 3 and Gereon Hüttmann2, 3
(1)
Thorlabs GmbH, Lübeck, Germany
(2)
Institute of Biomedical Optics, University of Lübeck, Lübeck, Germany
(3)
Medical Laser Center GmbH, Lübeck, Germany
27.1 Introduction
Optical coherence tomography (OCT) images three-dimensional biological tissues with micrometer resolution. While time-domain OCT required axial scanning of the imaging plane or the specimen, Fourier-domain OCT enabled parallel detection of all depths, which allowed to increase the acquisition speed by several orders of magnitude. When increasing the numerical aperture (NA) for achieving microscopic resolution, the advantage of Fourier-domain over time-domain OCT is lost. The resolution and sensitivity of FD-OCT imaging is only optimal within the Rayleigh range. Both degrade outside of the focal region, which shrinks with the square of the NA. The sensitivity is lost due to the confocal gating as photons from out-of-focus layers do not even reach the detector.
In full-field swept-source OCT, a parallel illumination and detection and the abandoning of the confocal gating allowed to maintain sensitivity over larger measurement depths [1, 2].
In digital holography (DH) entire wave fields, including their phase and amplitude, are captured, and the image information is calculated from the interference pattern. This allows for numerical refocusing in order to obtain images of the specimen over a larger measurement depth than provided by the focal depth [3–5]. But DH does not provide tomographic imaging, as no cross-sectional images are obtained.
Finally, by combining digital holography and full-field swept-source OCT, tomographic images are obtained, with optimal sensitivity and resolution spanning regions much larger than the focal range. Using numerical algorithms, comparable to the ones first shown in interferometric synthetic aperture microscopy (ISAM, [6–10]) and inverse scattering for full-field OCT [8, 11], the depth of focus can be extended, and thus, a depth-independent resolution and sensitivity can be obtained.
The combination of digital holography with time-domain and Fourier-domain OCT was shown by several groups. Massatsch et al. [12] demonstrated the combination of time-domain OCT with digital holography. However, when using time-domain OCT, axial scanning is still required. First optical sectioning using digital holography with multiple wavelengths was shown by Kim in 1999 [13], but cumbersome and inefficient reconstruction algorithms were used, and imaging quality was not comparable to OCT. The limitations were mostly due to the small number of wavelengths used. Later work used OCT technology to obtain better images, but in the applied reconstruction algorithms, the focus was fixed to a single layer, and thus, the principal advantage of digital holography – virtual refocusing – was not used [14, 15]. An efficient reconstruction using simulated full-field OCT data was shown using inverse scattering techniques but not demonstrated experimentally [8, 11]. Finally, a consequent combination of digital holography with full-field swept-source OCT was shown in holoscopy [16–18, 23]. The extended depth of focus in terms of sensitivity and resolution compared to standard confocal scanning OCT was demonstrated, and images were shown that demonstrate an imaging quality comparable to full-field swept-source OCT.
27.1.1 Sensitivity Improvement of Holoscopy
In FD-OCT the imaging depth resulting in optimal images is limited to the focus region, which extends over two Rayleigh lengths z R . The Rayleigh length at the Numerical Aperture (NA) is given by
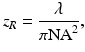 with λ being the wavelength. Therefore, for the total measurement depth d, only a ratio of 2z R /d of the B-scan shows optimal sensitivity and resolution. This motivates the definition of a photon efficiency of confocal OCT η confocal by
with λ being the wavelength. Therefore, for the total measurement depth d, only a ratio of 2z R /d of the B-scan shows optimal sensitivity and resolution. This motivates the definition of a photon efficiency of confocal OCT η confocal by
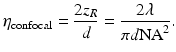 The photon efficiency for various measurement depths, ranging from 0.3 to 3 mm, at a central wavelength of 823.5 nm is shown in Fig. 27.1. The photon efficiency drops rapidly with increasing NA, and for microscopic NA around 1.0, it is several orders of magnitude smaller than the optimal value η confocal = 1.
The photon efficiency for various measurement depths, ranging from 0.3 to 3 mm, at a central wavelength of 823.5 nm is shown in Fig. 27.1. The photon efficiency drops rapidly with increasing NA, and for microscopic NA around 1.0, it is several orders of magnitude smaller than the optimal value η confocal = 1.
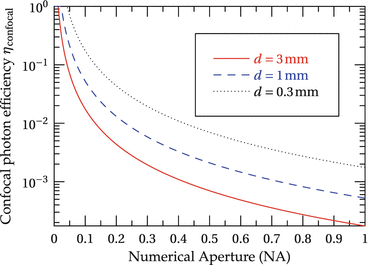
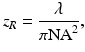
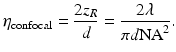

Fig. 27.1
Photon efficiency η confocal = 2z R /d for a confocal FD-OCT. The photon efficiency describes the relative amount of backscattered photons that can be used for imaging with optimal diffraction limited resolution and sensitivity
In holoscopy all photons backscattered within the NA are detected and provide optimal resolution when refocused to the plane in which they were scattered. Holoscopy thus allows in principle an optimal photon efficiency of η holoscopy ≈ 1. It is therefore more efficient than FD-OCT and allows either to increase the sensitivity and imaging speed or to reduce the light intensity on the specimen.
27.2 Digital Holography
In digital holography, a wave field O(x, y) of light scattered or reflected by the object is captured by recording the interference pattern of O(x, y) with a well-known reference wave R(x, y). The interference pattern I(x, y) can be described by
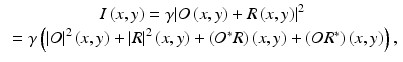 where γ is a factor considering camera sensitivity and scaling between squared field strength and measured intensity values and x and y denote coordinates of the camera pixels. With a known reference wave R(x, y), the wave field O(x, y) can be computed by multiplying with R/|R|2:
where γ is a factor considering camera sensitivity and scaling between squared field strength and measured intensity values and x and y denote coordinates of the camera pixels. With a known reference wave R(x, y), the wave field O(x, y) can be computed by multiplying with R/|R|2:
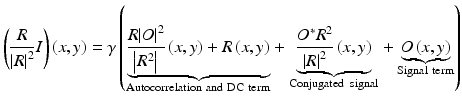 As in FD-OCT additional terms appear. Here, the autocorrelation term denotes the interference of the sample with itself. The DC term describes an offset to the entire image, created by object and sample wave fields. The signal term is the wave field that was captured from the object, and the conjugated signal is proportional to the complex-conjugated object wave field.
As in FD-OCT additional terms appear. Here, the autocorrelation term denotes the interference of the sample with itself. The DC term describes an offset to the entire image, created by object and sample wave fields. The signal term is the wave field that was captured from the object, and the conjugated signal is proportional to the complex-conjugated object wave field.
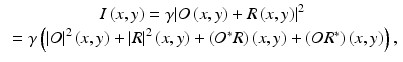
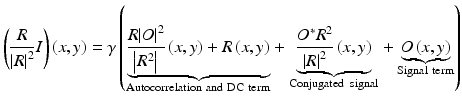
In digital holography the reference illumination on the camera is in most cases applied under an angle to the object wave (off-axis holography), resulting in a separation of all three terms after a two-dimensional Fourier transform of the acquired interference pattern I(x, y). In Fourier space the signal term can then be filtered, and disturbance of the non-signal terms can be minimized (see, e.g., [5]).
In FD-OCT similar terms arise in the spectral interference pattern, which disturb the final A-scan.
27.2.1 Propagation
Having obtained the object wave field O(x, y) does in general not give any information about the structures of the object itself, as the object field from a deep volume cannot be focused onto the camera, i.e., for large parts of the sample volume, only an unfocused image is obtained. To solve this issue, one can propagate the wave field numerically by computing its diffraction pattern in the appropriate plane. One effective way to do this is the angular spectrum approach (see, e.g., [4, 5, 19]).
Using this approach the wave field O(x, y) is first two-dimensionally Fourier transformed to obtain its angular spectrum, i.e., it is decomposed to plane waves propagating in different directions:
![$$ \tilde{O}\left({k}_x,{k}_y\right)=\mathrm{\mathcal{F}}\left[O\left(x,y\right)\right]=\int \mathrm{d}x\kern0.2em \mathrm{d}y\kern0.5em O\left(x,y\right){\mathrm{e}}^{-\mathrm{i}\left({k}_xx+{k}_yy\right),} $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_Eque.gif) The original field O(x, y) is then expressed as a superposition of plane waves exp(i(k x x + k y y)), each propagating in direction given by (k x , k y ) and with amplitude
The original field O(x, y) is then expressed as a superposition of plane waves exp(i(k x x + k y y)), each propagating in direction given by (k x , k y ) and with amplitude 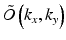
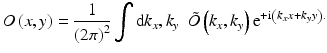 Each plane wave
Each plane wave
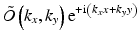 can be propagated in z-direction by multiplication with the phase factor
can be propagated in z-direction by multiplication with the phase factor
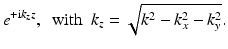 Thus, the propagation of the entire wave field O(x, y) is achieved by propagating the plane waves it is composed of. Mathematically the propagation of the diffracted field from a known wave position can be described by an operator, called propagator
Thus, the propagation of the entire wave field O(x, y) is achieved by propagating the plane waves it is composed of. Mathematically the propagation of the diffracted field from a known wave position can be described by an operator, called propagator 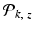 .
.
![$$ \tilde{O}\left({k}_x,{k}_y\right)=\mathrm{\mathcal{F}}\left[O\left(x,y\right)\right]=\int \mathrm{d}x\kern0.2em \mathrm{d}y\kern0.5em O\left(x,y\right){\mathrm{e}}^{-\mathrm{i}\left({k}_xx+{k}_yy\right),} $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_Eque.gif)
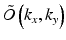
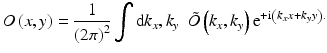
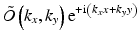
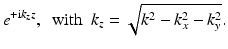
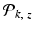 .
.The propagator is defined as
![$$ {\mathcal{P}}_{k,z}\left[O\left(x,y\right)\right]={\mathrm{\mathcal{F}}}^{-1}\left[{\mathrm{e}}^{+i{k}_zz}\mathrm{\mathcal{F}}\left[O\left(x,y\right)\right]\right], $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_Equ1.gif)
where k is the wavenumber and z denotes the propagation distance. The propagator yields results identical to the first Rayleigh-Sommerfeld diffraction integral [20].
![$$ {\mathcal{P}}_{k,z}\left[O\left(x,y\right)\right]={\mathrm{\mathcal{F}}}^{-1}\left[{\mathrm{e}}^{+i{k}_zz}\mathrm{\mathcal{F}}\left[O\left(x,y\right)\right]\right], $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_Equ1.gif)
(27.1)
27.3 Theory of Holoscopy
Holoscopy contains two critical steps: acquiring scattered object fields at multiple wavelengths by a camera and efficiently processing of the data to obtain tomographic images, which incorporates the reconstruction principles known from digital holography.
27.3.1 Basic Setups of Holoscopy
Setups that can be used for holoscopy are similar to the setups used in digital holography. Both techniques are based on the interference of a wave that is scattered or reflected by the sample and a well-known – usually spherical or plane – reference wave. The sample is illuminated with an extended, usually collimated, beam. The backscattered light is superimposed with the reference beam, and the resulting interference pattern is recorded. In contrast to digital holography, this is done in holoscopy for many wavenumbers using a swept-source laser and is thus comparable to swept-source OCT.
In general, no imaging optics are required for either technique, but the achievable lateral resolution is limited without using imaging optics. Digital holography and holoscopy can be used lensless or with microscope objectives to achieve high-resolution holoscopy. Schematic drawings of possible holoscopy setups are shown in Fig. 27.2a, b.
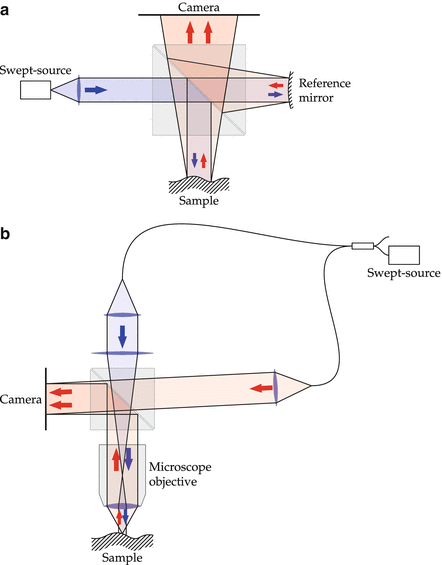

Fig. 27.2
(a) Schematic drawing of a lensless holoscopy setup. Coherent light of a known reference beam and light scattered from the sample are superimposed and digitized for many wavelengths. (b) Mach-Zehnder-type setup of a high-resolution holoscope
27.3.2 The Acquired Images
In holoscopy, the interference image I(x, y, k), which is caused by a superposition of a reference wave field R(x, y, k) and a sample wave field O(x, y, k) on the camera, is dependent on the wavenumber k. We assume that the fields R and O have been acquired for the entire plane, i.e., for all (x, y). In practice this is never the case, and limitations of the camera size will result in a limited resolution and/or lateral field of view. The only difference compared to digital holography (as shown in Sect. 27.2) is that the wavenumber k is now an additional variable as data are acquired for multiple wavenumbers. Additionally, it is assumed that the camera lies in the z = z 0 plane. The interference pattern in this plane is given by
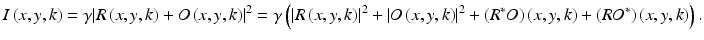
The meaning of the terms is identical compared to the case of digital holography: the term |R(x,y,k)|2 describes the absolute value of the reference field, which contributes mostly to the DC part of the recorded interference pattern. The term |O(x,y,k)|2 describes the interference of the object wave with itself (autocorrelation). Finally, 2Re(R ∗ O)(x, y, k) is the real cross-correlation term and contains the information of interest.
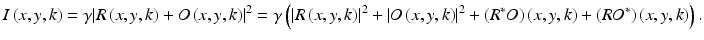
(28.2)
The reference wave is usually a plane or spherical wave, described by
![$$ R\left(x,y,k\right)={\displaystyle {\left.{A}_C(k){A}_R\cdot \exp \left[i\boldsymbol{k}\cdot \boldsymbol{x}+i{\phi}_0(k)\right]\right|}_{\boldsymbol{x}=\left(x,y,{z}_0\right),}} $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_Equ3.gif)
where k is the wave vector, which defines wavelength and propagation direction of the wave, z 0 is the camera plane, A C (k) is the relative amplitude spectrum, and A R describes the overall amplitude of the reference wave. ϕ 0(k) is the initial phase in the reference plane, in which the path length in the sample arm is the same as the one in the reference arm. In this plane, both reference and sample waves, have the same phase for all wavenumbers k. For on-axis imaging geometry, the reference wave is propagating perpendicular to the camera. To reduce spatial fringe frequencies on the camera, a spherical reference wave can be used similar to digital holography (see, e.g., [4]).
![$$ R\left(x,y,k\right)={\displaystyle {\left.{A}_C(k){A}_R\cdot \exp \left[i\boldsymbol{k}\cdot \boldsymbol{x}+i{\phi}_0(k)\right]\right|}_{\boldsymbol{x}=\left(x,y,{z}_0\right),}} $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_Equ3.gif)
(28.3)
In case of the Michelson-type setup, as shown in Fig. 27.2a, the spherical wave can be created by subjecting a plane wave to a reference mirror with a given focal length f. In a Mach-Zehnder-type setup, a spherical wave can be created by focusing the light with a suitable lens. The following will describe the Michelson setup. Adjusting the formalism for a Mach-Zehnder-type setup is straightforward, as the introduction of a spherical reference wave in our computations is equivalent to introducing a numerical lens. Both lead to identical phase factor multiplications [19].
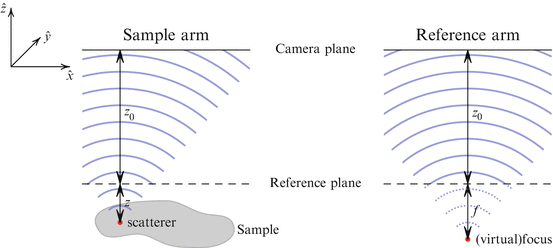
Let the distance from the reference mirror to the camera be denoted z 0. Then the reference field is given by
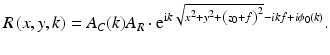
This describes a spherical wave originating at a distance f behind the reference plane (Fig. 27.3).
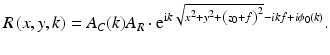
(27.4)

Fig. 27.3
Coordinate systems as used in the computation of the sample (left) and reference (right) wave field. The sample is made of several point scatterers whose fields are superimposed in the camera plane. In this case, the reference wave is a spherical wave with a (virtual) origin behind the reference plane. The configuration can be achieved by using a spherical reference mirror as shown in Fig. 27.2a
The fraction of light backscattered from the sample at a transversal position (x, y) at a distance z from the reference plane is given by the scattering potential η(x, y, z), thereby neglecting any angular dependence of the backscattering. The collimated light enters the sample, moves a distance z to the scatterer, is backscattered, and then is propagated by a distance z + z 0 to the camera. Assuming the validity of the first-order Born approximation [21], which assumes single scattering and a constant incident wave field throughout the volume, the object field O(x, y, k) and its angular spectrum Õ xy (k x , k y , k) in the camera plane are just a superposition of the fields generated by the backscattering in each depth, i.e.,
![$$ \begin{array}{l}\kern2.12em O\left(x,y,k\right)={A}_O{A}_C(k)\cdot \int \mathrm{d}z\;{\mathcal{P}}_{k,{z}_0+z}\left[\eta \left(x,y,z\right){\mathrm{e}}^{\mathrm{i}kz}{\mathrm{e}}^{\mathrm{i}{\phi}_0(k)}\right],\\ {}\phantom{\rule{0ex}{1.52em}}\kern1.12em {\displaystyle {\tilde{O}}_{xy}}\left({k}_x,{k}_y,k\right)={A}_O{A}_C(k)\cdot \int \mathrm{d}z\;{\mathrm{e}}^{\mathrm{i}{k}_z\left(z+{z}_0\right)+\mathrm{i}kz}\cdotp {\mathrm{e}}^{\mathrm{i}{\phi}_0(k)}\cdot {\displaystyle {\tilde{\eta}}_{xy}}\left({k}_x,{k}_y,z\right).\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_Equ5.gif)
The coordinate system as used for reference and object field is illustrated in Fig. 27.3.
![$$ \begin{array}{l}\kern2.12em O\left(x,y,k\right)={A}_O{A}_C(k)\cdot \int \mathrm{d}z\;{\mathcal{P}}_{k,{z}_0+z}\left[\eta \left(x,y,z\right){\mathrm{e}}^{\mathrm{i}kz}{\mathrm{e}}^{\mathrm{i}{\phi}_0(k)}\right],\\ {}\phantom{\rule{0ex}{1.52em}}\kern1.12em {\displaystyle {\tilde{O}}_{xy}}\left({k}_x,{k}_y,k\right)={A}_O{A}_C(k)\cdot \int \mathrm{d}z\;{\mathrm{e}}^{\mathrm{i}{k}_z\left(z+{z}_0\right)+\mathrm{i}kz}\cdotp {\mathrm{e}}^{\mathrm{i}{\phi}_0(k)}\cdot {\displaystyle {\tilde{\eta}}_{xy}}\left({k}_x,{k}_y,z\right).\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_Equ5.gif)
(27.5)
27.3.3 The Phase-Corrected Propagator and Object and Reference Field
Propagating a wave field by the propagator ![$$ {\mathcal{P}}_{k,z}\left[\cdot \right] $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_IEq3.gif) will change the overall phase of the field. In OCT, depth information is contained in the phase of the wave field, and thus, arbitrarily changing the phase will destroy this depth encoding. If a wave is propagated by a distance z by the propagator
will change the overall phase of the field. In OCT, depth information is contained in the phase of the wave field, and thus, arbitrarily changing the phase will destroy this depth encoding. If a wave is propagated by a distance z by the propagator ![$$ {\mathcal{P}}_{k,z}\left[\cdot \right] $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_IEq4.gif) , its overall phase will change by eikz . For focusing of the object without changing the phase information, and thus without changing the depth encoding, the propagator needs to be adapted accordingly. This motivates the definition of a phase-corrected propagator
, its overall phase will change by eikz . For focusing of the object without changing the phase information, and thus without changing the depth encoding, the propagator needs to be adapted accordingly. This motivates the definition of a phase-corrected propagator
![$$ {\mathcal{P}}_{k,z}^0\left[\cdot \right]\equiv {\mathrm{e}}^{-\mathrm{i}kz}{\mathcal{P}}_{k,z}\left[\cdot \right]. $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_Equi.gif) The phase-corrected propagator is just a mathematical construct. Physical propagation of the wave field in free space will inevitably change the phase of the wave. Nevertheless, computations simplify significantly when introducing the phase-corrected propagator.
The phase-corrected propagator is just a mathematical construct. Physical propagation of the wave field in free space will inevitably change the phase of the wave. Nevertheless, computations simplify significantly when introducing the phase-corrected propagator.
![$$ {\mathcal{P}}_{k,z}\left[\cdot \right] $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_IEq3.gif) will change the overall phase of the field. In OCT, depth information is contained in the phase of the wave field, and thus, arbitrarily changing the phase will destroy this depth encoding. If a wave is propagated by a distance z by the propagator
will change the overall phase of the field. In OCT, depth information is contained in the phase of the wave field, and thus, arbitrarily changing the phase will destroy this depth encoding. If a wave is propagated by a distance z by the propagator ![$$ {\mathcal{P}}_{k,z}\left[\cdot \right] $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_IEq4.gif) , its overall phase will change by eikz . For focusing of the object without changing the phase information, and thus without changing the depth encoding, the propagator needs to be adapted accordingly. This motivates the definition of a phase-corrected propagator
, its overall phase will change by eikz . For focusing of the object without changing the phase information, and thus without changing the depth encoding, the propagator needs to be adapted accordingly. This motivates the definition of a phase-corrected propagator![$$ {\mathcal{P}}_{k,z}^0\left[\cdot \right]\equiv {\mathrm{e}}^{-\mathrm{i}kz}{\mathcal{P}}_{k,z}\left[\cdot \right]. $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_Equi.gif)
The reference as well as the object wave field, given by Eqs. 27.4 and 27.5, travel the same optical path length from the light source to the reference plane and have an identical time-dependent phase term ϕ 0(k), and common phase factors occur in reference and sample that need to be taken into account during reconstruction. In general, changing the overall phase of the two fields in exactly the same manner does not change the measurable quantity I(x, y, k). For the following computations, it is therefore advantageous to redefine and simplify the phases of object and reference field, instead of using the previously obtained and physically motivated formulas, similar to the way the phase-corrected propagator replaces the propagator Eq. 27.1.
The phase-corrected reference wave field is therefore introduced by
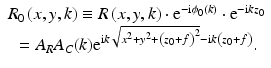
For f → 0 the origin of the reference wave goes to the reference plane. Holograms of this kind are also referred to as Fourier holograms as they can be reconstructed in paraxial approximation by means of a simple Fourier transform (see, e.g., [4]).
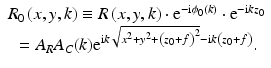
(27.6)
The phase-corrected object wave field is accordingly defined by
![$$ {O}_0\left(x,y,k\right)\equiv O\left(x,y,k\right)\cdot {\mathrm{e}}^{-\mathrm{i}{\phi}_0(k)}\cdot {\mathrm{e}}^{-\mathrm{i}k{z}_0}\kern1.12em ={A}_O{A}_C(k){\displaystyle \int \mathrm{d}z\;{\mathcal{P}}_{k,{z}_0+z}^0\left[\eta \left(x,y,z\right){\mathrm{e}}^{\mathrm{i}2kz}\right]}. $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_Equ7.gif)
It is worthwhile to note the similarity to the standard FD-OCT cross-correlation term, except for the phase-corrected propagator ![$$ {\mathcal{P}}_{k,{z}_0+z}^0\left[\cdot \right] $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_IEq5.gif) . If the effect of the propagator can be reverted, images can be reconstructed similar to FD-OCT reconstruction by a Fourier transform. The effect of a propagator also arises in standard FD-OCT, but its influence is neglectable since FD-OCT works near the focal plane.
. If the effect of the propagator can be reverted, images can be reconstructed similar to FD-OCT reconstruction by a Fourier transform. The effect of a propagator also arises in standard FD-OCT, but its influence is neglectable since FD-OCT works near the focal plane.
![$$ {O}_0\left(x,y,k\right)\equiv O\left(x,y,k\right)\cdot {\mathrm{e}}^{-\mathrm{i}{\phi}_0(k)}\cdot {\mathrm{e}}^{-\mathrm{i}k{z}_0}\kern1.12em ={A}_O{A}_C(k){\displaystyle \int \mathrm{d}z\;{\mathcal{P}}_{k,{z}_0+z}^0\left[\eta \left(x,y,z\right){\mathrm{e}}^{\mathrm{i}2kz}\right]}. $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_Equ7.gif)
(27.7)
![$$ {\mathcal{P}}_{k,{z}_0+z}^0\left[\cdot \right] $$](/wp-content/uploads/2017/03/A76297_2_En_28_Chapter_IEq5.gif) . If the effect of the propagator can be reverted, images can be reconstructed similar to FD-OCT reconstruction by a Fourier transform. The effect of a propagator also arises in standard FD-OCT, but its influence is neglectable since FD-OCT works near the focal plane.
. If the effect of the propagator can be reverted, images can be reconstructed similar to FD-OCT reconstruction by a Fourier transform. The effect of a propagator also arises in standard FD-OCT, but its influence is neglectable since FD-OCT works near the focal plane.27.3.4 Obtaining the Phase-Corrected Object Wave Field
Interference of the phase-corrected object and reference wave gives the same intensity distribution as real physical waves:
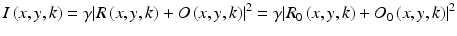 and consequently also Eq. 27.2 still holds, if R and O are replaced by R 0 and O 0, respectively. Hence, the phase-corrected object wave field can be calculated from the acquired interference patterns.
and consequently also Eq. 27.2 still holds, if R and O are replaced by R 0 and O 0, respectively. Hence, the phase-corrected object wave field can be calculated from the acquired interference patterns.
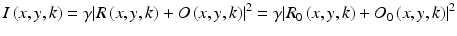
27.3.4.1 On-Axis Geometry
The measured intensity I(x, y, k) contains two conjugated parts R 0∗ O 0 and (R 0∗ O 0)∗, which are referred to as twin images in holography.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


