Fig. 13.1
A simple object, data, and image combination to illustrate the process of inference
Unfortunately, in practice, we usually do not have the possible objects narrowed down to two possibilities, and there are a nearly unlimited number of data observations one could make for these objects. While a rigorous enumeration of all possibilities is almost always not practical or even possible, we can still specify the general properties of what is known about the object and tailor the signal processing to produce images of these objects consistent with the data and the prior knowledge of the object. Within the limits of the available computational devices and methods, signal processing can help relieve the operator of some of the burden of recognizing and classifying the image by removing artifacts and noise in the image that is not consistent with what the object is believed to be.
There are two properties that a useful signal processing method must have. First, a method must be stable. This means that very small changes in the data should not produce large changes in the reconstructed image or ultimately in the object that is believed to correspond to the data. This is necessary so that the image is robust to the variations in the data produced by noise and measurement error. Also, there should be a unique image estimate corresponding to a particular data set. This is so that the operator is not confronted with one of many possibly very different images given the same data. Both of these problems can be addressed partially by the use of regularization. Regularization is a constraint on the image that specifies aspects of the image that cannot be determined by the data. For example, a common regularization method penalizes the energy of an image. If an OCT system is designed to measure an object using wavelengths between 1,250 and 1,350 nm, the instrument does not provide information about the scattering of the object outside of this bandwidth. By minimizing the energy of the image, the estimate of the scattering of the object outside the bandwidth of the OCT system, say between 500 and 600 nm, is estimated to be zero. This is a reasonable assumption and one that is commonly made (implicitly or explicitly) when analyzing OCT data. By examining the stability, uniqueness, and the properties of an image that a given signal processing algorithm assumes, one can better understand whether a given signal processing algorithm will be useful in a specific situation.
13.2 Speckle Reduction and Signal Improvement
Speckle is one of the most distracting artifacts of OCT images (and other coherent ranging techniques such as ultrasound). It is often difficult to separate the features that are caused by speckle, and those of other features of interest. However, the phenomenon of speckle is what enables methods such as OCT to be useful. Because scatterers tend to be randomly placed in most objects, every frequency band in which the object can be probed contains some useful details of the object. This is why most coherent ranging techniques are useful in practice. If scatterers were not randomly placed so that speckle did not occur, it is possible that the object may not yield any detail whatsoever in the frequency band in which it is being probed (an example is when one images a Bragg grating with a resonant frequency outside the probed bandwidth). Unfortunately, if one is distinguishing detail at the resolution limit of the instrument, it is likely that it will be modulated by speckle and therefore appear very noisy.
Speckle occurs when the scatterers are randomly placed, and their backscattered reflections each superimposes with a random phase and amplitude in the OCT interferogram. This can be visualized as a “random walk” of two-dimensional vectors [1], each vector representing the complex-valued reflectance of each unresolved scatterer. The sum of these vectors is approximated by a complex-Gaussian random variable [1], which has a length given by a Rayleigh probability distribution. Note that this implies that the magnitude squared of the vector has an exponential or Boltzmann probability distribution. When multiple polarizations of return signal are accounted for, the magnitude squared of the reflectance conforms more to a gamma distribution [2, 3].
This persistent problem has been addressed by several different approaches. One method [4], the sticks method adapted from ultrasound, was used to despeckle coronary artery images. This method fits short line segments of various orientations to features in the image to approximate the boundaries of the vessel. Another method [5] applies the rotating kernel transformation to coronary images, which matches edges in the image to a set of binary-valued two-dimensional square kernels to enhance the edges and suppress speckle noise. A promising technique [6] uses an undecimated wavelet filter transformation on the logarithm of the magnitude of the OCT image to remove the uncorrelated speckle features but retain the scale-invariant features that produce the largest wavelet coefficients. This method enhances the discrimination of noise by exploiting the correlations between wavelet coefficients at multiple scales due to object features. The logarithm of the magnitude is processed because speckle can be modeled as multiplicative noise to the image, which becomes additive noise once the logarithm is taken. Additionally, a multidimensional wavelet method utilizes correlations in time-series data to suppress noise via decorrelation [7]. An example of denoising using this technique is shown in Fig. 13.2. A similar method, except based on the curvelets transform, has also been demonstrated as shown in Fig. 13.3 [8, 9]. Another speckle suppression method [10] simultaneously constrains the magnitude to match a blurred version of the image, while retaining the detail by constraining the image to fit the data in a least-squares sense. The blurred OCT image acts as a “default” image that is used to assign the magnitude of the data where the data leaves the magnitude of the reconstructed image unspecified. The actual constraint used is a relative entropy constraint called the I-divergence [11] between the default image and the reconstructed image.
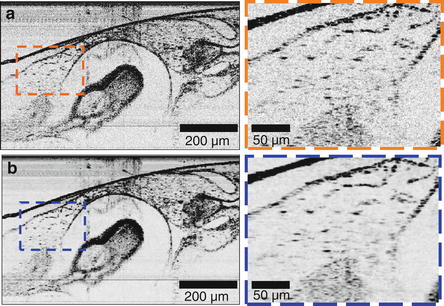
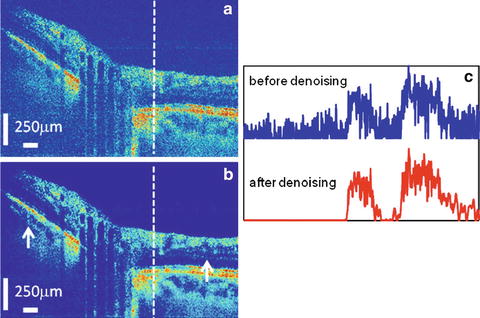

Fig. 13.2
Representative frame of multidimensional denoising of a sequence of OCT images acquired in real time. (a) Originally acquired data of Xenopus laevis tadpole. (b) Image after denoising. The zoomed-in figures at the left panel correspond to the boxed regions (Images used with permission from [7])

Fig. 13.3
Image of an optical nerve head (a) before and (b) after speckle reduction by shrinkage in the curvelet domain. Depth-resolved line-plots (c) along the vertical dashed lines in (a and b) illustrate speckle reduction, making features more distinguishable (white arrows) (Images used with permission from [8])
One straightforward way to remove the effects of speckle is to incorporate several images into a single image [2, 3]. The speckle effect occurs because most objects have features at length scales smaller than the smallest resolvable area of an OCT instrument. Speckle is caused by the interference between randomly placed scatterers that are individually unresolvable due to the finite bandwidth and focused spot size of the OCT instrument. In OCT images, speckle appears as a random modulation to the demodulated amplitude image due to the interference between the scattered waves from these unresolved scatterers. Unfortunately, in practice, the features caused by the random interference of speckle and those of other features of interest are frequently indistinguishable.
Two or more images of the same object that does not itself change between the image acquisition sequences will exhibit identical speckle patterns even if the noise is independent between the images. Therefore, if these images are averaged together, the speckle pattern will remain even if the signal-to-noise ratio is improved. To reduce speckle, the averaged images must each be slightly different by probing different coherent superpositions of the sub-resolution scatterers that produce the speckle. To achieve this, one may employ a diversity mechanism intended to vary the phase of the interference between the sub-resolution scatterers. The diversity mechanism ideally produces an independent amplitude modulation due to speckle at each resolvable point in each image. By measuring different combinations of interference between the sub-resolution scatterers, the density of scatterers in the image can be better estimated by averaging together the randomized amplitudes of the constituent images.
There are four main diversity methods used to reduce speckle. Frequency compounding [12] merges the images of the same object taken in two different optical frequency bands. Most particles will scatter at wavelengths in the near infrared (NIR). By choosing two different frequency bands in the NIR, the phase shift of the interference between scatterers is altered to produce two different speckle patterns in each band. Because the speckle patterns in both frequency bands are largely uncorrelated, compounding them significantly decreased the speckle in the image. Polarization diversity [13] measures the same object with orthogonal polarizations with the goal of producing different speckle patterns for each polarization that can be averaged. Angular compounding [14–16] measures the sample with various tilts of the axial scan relative to the transverse scan direction, rather than always having the axially focused beam normal to the transverse scanning direction. By illuminating the scatterers in the object at different angles, different combinations of the scatterers are measured to change the speckle pattern. Finally, spatial compounding [17] reduces speckle noise by averaging together various parts of an image, which is helpful when the object properties are uniform such as a sample of human skin. In some recent methods, an increasing strain is applied to the sample, which effectively decorrelates the speckle between successive B-scans. Incoherent averaging of these decorrelated images reduces the speckle noise [18, 19]. In another method, image registration followed by averaging of multiple B-scans is used to reduce speckle [20].
Similar signal processing methods have been developed to remove and suppress image artifacts commonly seen in spectral-domain OCT systems. Fixed pattern noise artifacts which show up in OCT images as horizontal lines are the most prominent. These artifacts can come from the non-flatness of the reference spectrum, spectral structure in the source spectrum, and optical interferences from spurious back-reflections [21]. These artifacts can be removed by measuring the reference spectrum in the absence of the sample and subtracting it from the measured spectrum. The reference spectrum can be estimated from the acquired data itself. A common method is to average several A-scans, and due to the sample inhomogeneity, the random phase distribution would wash out the fringe pattern leaving behind the reference spectrum. Subsequently, each interferometric spectrum is subtracted by the reference spectrum to remove the fixed-pattern noise. However, a small number of high-amplitude back-reflections mainly due to the air–tissue interface can cause errors in estimating the mean reference spectrum [21, 22]. A number of alternative approaches to overcome this limitation of the mean-spectrum subtraction method have been proposed. In one technique called the minimum-variance mean-line subtraction, each horizontal line is divided into segments and the mean value corresponding to the segment having the minimum variance is assigned to a given axial position. As the segment containing high-amplitude reflection points would exhibit higher variances, this method can potentially give more robust estimates [21, 23]. Another method is based on the median estimator which is known to be less sensitive to high-amplitude data points. In this method, a complex median value is calculated for each axial position and this complex median A-line is then subtracted from each of the A-lines to remove the fixed-pattern noise artifacts [21–23].
One of the simplest and most intuitive ways in which images can be enhanced is to take several images of the same object and incorporate these into a single image with superior resolution and/or signal-to-noise ratio to any of the individual images. The resultant denoised image is often the average of the samples of the individual images. There are two reasons that signal averaging is done to OCT images. This first is to improve the signal-to-noise ratio of the resultant image. If one can assume that the noise component of each of the constituent images is independent of each other, then averaging together several images of the same object (which are ideally identical except for different realizations of added noise), the average of the images will converge to an image with a lower variance than the constituent images. This averaging can be done on the interferograms of the OCT axial scans or more often is performed on the demodulated gray-scale image. While this method works, the penalty is a slower data acquisition which is often not acceptable in practice.
Recent attention has been given to compressive sampling (CS) strategies for image recovery in medical sensors [24, 25]. The idea behind CS is to exploit an aspect of sparsity in a transform domain where fewer measurements can be used to recover missing data with higher accuracy. Of course, this is reliant on the accuracy of your choice of transform domain. This means that the choice of sparse representation is a key to recovering good image quality. Some authors have described a method that exploits the sparsity in point-like scattering within an A-mode OCT scan [26, 27]. By using the fact that the frequency domain representation of a sparse numbers of point-scatterers is overdetermined, fewer measurements of the Fourier signal space can be used to form a reconstruction. Other methods rely on the spatial sampling as the sparsity constraint [28, 29]. For instance, if one intends to reconstruct an object with three to five times oversampling, then the redundancy in the measurements can be exploited by using CS. That is, fewer measurements can be used to reconstruct the object to full oversampled resolution. This method has been demonstrated with both B-mode and 3-D imaging in real-time systems [28]. One study evaluated the performance of different transform domains for recovery of OCT volumes from sparse data sets [30]. The Fourier basis, wavelet basis, Dirac basis, discrete-cosine basis (DCT), and surfacelet basis are examples of common bases examined. Another study showed an approach for using a modified-CS algorithm to increase the local contrast, the signal-to-noise ratio (SNR), and the contrast-to-noise ratio (CNR) [31]. Further quality improvements are gained from averaging the reconstructions.
13.3 Deconvolution and Spectral Shaping
Another common goal of post-processing is to achieve the best resolution and highest signal-to-noise ratio that the data will allow. In OCT, the primary limiting factor for axial resolution is the bandwidth of the source, and the limiting factor for transverse resolution is the focused spot size. The process of deconvolution attempts to extrapolate somewhat more detail from the data limited by the signal-to-noise ratio of the data. In addition, deconvolution can reject noise and remove sidelobes from the image.
To understand what deconvolution does, we consider Fig. 13.4 which contains the interferogram of an axial scan of a reflection off of a glass–air interface in an OCT system. This interface between glass and air is extremely abrupt and so is much sharper than the features that can be resolved with a typical OCT system. The length of the interferogram in this case is limited by the bandwidth of the source and not by the detail of the object.
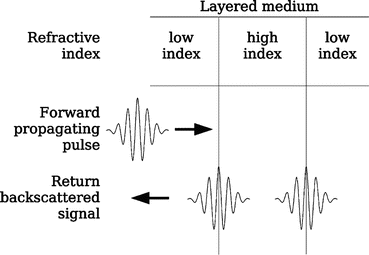

Fig. 13.4
A diagram showing how an optical pulse reflects off of interfaces between regions of varying indices of refraction. Even though the interfaces are sharp, the reflections are all copies of the original pulse and therefore the length of the pulse
Because we know this interferogram corresponds to a single reflection, we may decide to infer the location and the position of the surface as the peak of the interferogram. The error in the estimate of the position of the surface is potentially much less than that suggested by the width of the interferogram, because we already have knowledge that there is only one reflector. By using a priori knowledge about the object and the optical source spectrum, scatterers can be better resolved than would be suggested by the interferogram width alone.
If there are multiple reflections, each of the reflections produces an interference pattern that is superimposed on the interferogram. The mathematical operation that finds the interferogram caused by a set of reflectors by superimposing the interference patterns for each reflector is called convolution. Therefore, the operation of finding the reflectors based on the interferogram is called deconvolution. Because of the relatively wide width of the interferograms and noise, deconvolution is necessarily an imperfect process where the reflectors corresponding to a particular interferogram cannot be recovered with certainty.
A simple way of locating reflectors in an OCT image is based on the CLEAN algorithm [32, 33]. In this algorithm, one attempts to locate the highest reflectivity scatterer in the data by scanning for the largest magnitude interference pattern. The position and magnitude of this interference pattern is used to infer the location of the scatterer in the final image, and then the interference pattern due to the scatterer is subtracted from the data. This process is repeated on the data to successively infer the positions and magnitudes of weaker scatterers as they are subtracted from the data. Because this method identifies individual point scatterers, it tends to work best on objects with discrete particles. However, many biological specimens are not similar to a collection of point-like reflectors. In one method, it is assumed that the signal at each point is superimposed by the sidelobes of other points in the same A-scan. A method to suppress the sidelobes called gradual iterative subtraction is implemented by iteratively subtracting the influence of the sidelobes from other points in an A-scan [34].
Rather than determining the position and magnitude of every point scatterer in the sample, most deconvolution methods produce an image where the features appear more point-like. This is done by applying a post-processing filter to concentrate the signal of a scatterer around its center position on the interferogram. Highly nonuniform spectra will cause the image of a point scatterer to have many and large-amplitude sidelobes. Sources such as ultrahigh numerical aperture fibers [35, 36] and microstructured fibers [37, 38] produce a large bandwidth, but the sidelobes caused by these sources can severely degrade the practically achievable resolution. Deconvolution methods help improve resolution, reject noise outside of the laser spectrum, and make the resolution more robust to variations in the source spectrum.
To apply these methods, the interferograms themselves [39] need to be sampled rather than just the demodulated envelope. A method of deconvolution of the demodulated magnitude data [40] has been achieved, but may have problems accounting for interference effects between scatterers. Many OCT systems provide only demodulated interference fringes. This method uses a positivity constraint to somewhat overcome the lack of phase information. The benefit of directly processing the interferograms is that they are typically linear in the scattering amplitude of the sample (in the weak scattering approximation). One of the simplest methods [41] infers what the image would have looked like if it was taken with a low-sidelobe Gaussian source rather than the actual source used. This method effectively numerically “reshapes” the spectral envelope of the laser to become Gaussian-like which helps reduce sidelobes, perhaps at the expense of increasing noise. Other methods [42] apply a linear filter that inverts the source spectrum shape, to attempt to make the numerically reshaped source spectrum uniform. Another method applies a filter that provides the linear least-squares estimate of the sample scattering [43], taking into account the quantum efficiency and photon noise of photodetection. A further method [44] modifies this result to reduce sidelobes. Additional methods use deconvolution in conjunction with dispersion management to minimize the point-scatterer image size [45]. Another paper describes regularized inversion methods for deconvolution that mitigate the depth-dependent blurring of the transverse point spread function caused by the focusing optics [46]. An example is shown in Fig. 13.5 where after the deconvolution operation, the point scatterers in the image are sharper and better defined. In a similar method described, a set of Gaussian PSFs of different spot sizes were used to deconvolve defocused images using the Richardson–Lucy algorithm. The Richardson–Lucy algorithm is based on the maximum-likelihood solution in regard to Poisson statistical data. One study introduced a method to improve the resolution on OCT system by step-frequency encoding [47]. In this method, two A-scans of slightly different frequencies are added together resulting in a beating pattern which reduces the FWHM of the central lobe in the interferograms. However, the beating also introduces sidelobes in the interferograms which can lead to artifacts in the reconstructed images [47].
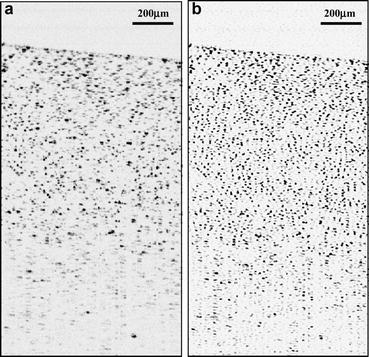

Fig. 13.5
Deconvolution using the Richardson–Lucy algorithm on a tissue phantom. (a) Original and (b) Richardson–Lucy corrected image (Images used with permission from [46])
While many of these methods successfully mitigate the blurring of OCT, a full formalized quantitative deconvolution of the focusing optics is solved in interferometric synthetic aperture microscopy (ISAM) [48]; the details of which can be found in Chap. 31, “Interferometric Synthetic Aperture Microscopy (ISAM)”.
13.4 Dispersion Correction
Apart from speckle, the chromatic dispersion of the OCT signal is one of the most image-degrading distortions. Dispersion appears in OCT images as the blurring and interference of adjacent reflectors. A signal pulse propagating through a dispersive medium tends to develop a “chirp,” so that the signal increases or decreases in frequency as it passes a particular point in the medium. This changes a formerly sharp point in an image into a blurred region within an axial scan. Dispersion degrades the axial resolution because of this blurring. However, dispersion can be corrected. A simple way to do this is to insert a dispersive medium into the reference arm to balance the dispersion of the sample signal. However, it is desirable to correct dispersion using digital post-processing rather than a physical adjustment. Signal processing is more flexible and can adapt to the dispersion of the medium of the object. In addition, it is possible to automatically adjust digital post-processing without necessarily knowing the medium dispersion beforehand.
The dispersion of a medium is usually characterized by a dispersion relation. This relation can be specified in a number of ways: commonly by the index of refraction as a function of wavelength or the spatial frequency wavenumber in the medium as a function of temporal frequency. This dispersion determines the total propagation phase a particular temporal frequency component of the signal acquires when traveling a certain physical distance in the medium. By applying the opposite phase to each frequency component of the detected interference signal in post-processing, the effect of dispersion can be cancelled out. This method has been successfully demonstrated on OCT interferograms [49, 50] to produce the digital equivalent of optical dispersion balancing. The method is implemented as a cross-correlation and therefore can be implemented together with other convolution signal processing techniques as used for resolution enhancement, sidelobe reduction, and noise reduction.
One disadvantage of optical or digital dispersion balancing is that the dispersion is only compensated at one depth in the axial scan. To overcome this, consider that the interferogram in OCT is typically measured in the time domain using a delay line. The interferogram may be Fourier analyzed to find the temporal frequencies in the measured interferogram. Each temporal frequency has a corresponding spatial frequency in the sample medium. Because of medium dispersion, the spatial and temporal frequencies in media are not necessarily proportional to each other, as they are in free space. The relationship between temporal and spatial frequency is given by the medium dispersion relation. Compensating for material dispersion involves changing the coordinates of the Fourier representation of the interferogram from temporal frequency to spatial frequency. In practice, this is achieved numerically by a resampling or “warping” of the Fourier space. This process has been demonstrated [43, 51] to correct the dispersion for all of the points in the axial scan simultaneously. This resampling method can be performed more easily in spectral domain OCT [51] where the interferogram data is already measured in the Fourier domain and needs to be resampled anyways to compensate for nonlinearities in the spectrometer. Parameterizing a Taylor series expansion of the frequency-dependent dispersion often allows estimation of the dispersion correction [52].
In addition, it is possible in some cases to determine the amount of dispersion directly from the data without previous knowledge of the composition of the sample. A method of automatically finding the dispersion parameters minimizes the entropy of the image given a set of dispersion parameters [51]. Minimizing entropy tends to produce point-like and sharp features in the reconstructed image. Because uncorrected dispersion is expected to blur out the image, minimizing entropy tends to favor the images with the least dispersion. The method adjusts trial dispersion parameters and recomputes an image corrected by the trial parameters, searching for the parameters that produce an image with minimum entropy. Others find the best parameters by using a metric that minimizes the total number of points in the axial scan above some threshold [53].
Several others have described approaches to achieve dispersion compensation with similar results using noteworthy estimation techniques or advanced interpolation schemes. One paper describes a method in analogy to the Shack–Hartmann wavefront sensor, which provides an equivalent solution [54]. Here a short-time Fourier transform provides a means to calculate the nonlinear phase. A fractional Fourier transform has been used to achieve an optimal rotation of the time-frequency plane for correcting second-order dispersion [55]. Nonuniform discrete Fourier transforms or nonuniform fast Fourier transforms are methods of correcting the nonlinear frequency-dependent dispersion effect [56, 57]. These transforms perform as highly accurate band-limited interpolators. Additional dispersion compensation methods have been developed for nonconventional scanning methods, such as an electro-optical modulator [58]. This method involves making two measurements with a mirror at two different depths and subtracting the phases of the spectral fringes to get the resampling parameters.
To see the effect of dispersion correction on OCT axial scan data, Fig. 13.6 shows the measured interferogram before and after correction. This data is measured from the air–glass and polymer–glass interfaces of a polydimethylsiloxane microfludic channel. By applying a resampling to the interferogram in the Fourier domain, the effect of material dispersion can be compensated for, to restore the bandwidth-limited resolution. An example of dispersion compensation applied to data in a tadpole image is shown in Fig. 13.7. In this case, the dispersion parameters were inferred from the image itself and then were used to correct the image.
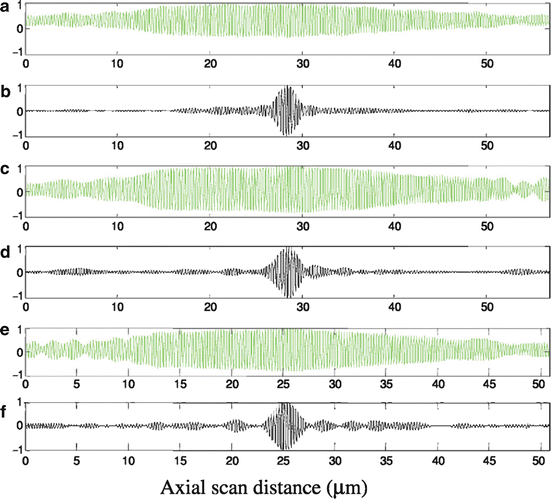
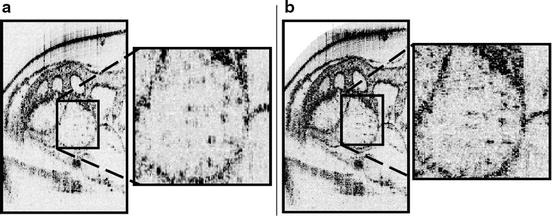

Fig. 13.6
Interferograms of reflections of air-glass and polymer-glass interfaces measured by OCT from a polydimethylsiloxane microfluidic channel. Parts (a), (c), and (e) are the interferograms before digital dispersion correction and (b), (d), and (f) are after correction (Image used with permission from [43])

Fig. 13.7
Example of automatic removal of dispersion artifacts from an image of Xenopus laevis tadpole. The image (a) is the original OCT image, and (b) is the image with the dispersion parameters inferred from the image, and then used to remove the speckle from the image. This method uses an entropy minimization criterion to determine the dispersion parameters (Image used with permission from [51])
In swept source (SS-) OCT, the sweep of the wavelength happens over a time frame, whereby phase coherency can be lost with motion. The motion induces a Doppler effect on the chirp sweep, which has a similar appearance to that of dispersion. A method of cross-correlation of sub-bandwidth reconstructions has been used to compensate for this motion-induced dispersion [59]. Other OCT modalities, where the compressed pulse is used for imaging, do not have this effect within the A-scans. In the next section, these motions that affect the consecutive A-scans, and motion compensation algorithms, are discussed.
A sample having a nonuniform medium can also suffer other distortions due to the refraction of the focused OCT beam as it scans through the sample. The refraction of the beam can change the apparent dimensions of the sample and the apparent locations of scatterers in the sample. It is then desirable to find the true spatial locations of scatterers inside the medium with knowledge of the refractive indices of the layers that comprise the medium. A method has been proposed [60] to correct for the refraction of the object and was demonstrated on a phantom and on the anterior chamber angle of a human eye. This method can correct the nonlinear scanning profile of a resonant scanning delay line and also non-telecentric imaging distortions. An example of an image corrected this way is given in Fig. 13.8. It accounts for the refraction of the OCT beam at the surfaces of the object by using ray tracing. Another method [61] uses the distortions caused by the refractive index variations to find the refractive index of the medium itself. Another method [62, 63] measures the refractive index by using coherence gating to measure the delay between light scattered from two foci in the medium along the axial scan. In another approach, the refractive index and thicknesses of multilayered phantoms were calculated by utilizing a matrix formulation of Fresnels’s equations [64]. One study used the Delaunay triangulation method to represent the surfaces in ocular images followed by 3-D ray tracing to correct for optic distortions caused by refractive index variations [65]. With knowledge of the refractive index, it seems likely that the refraction of a non-layered medium can be corrected as well.
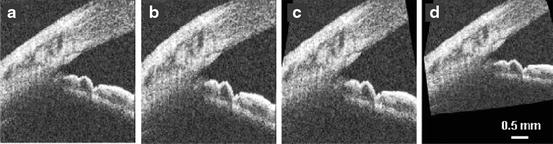

Fig. 13.8
Example of refraction correction of an image of the anterior chamber angle of a human eye. Image (a) is the raw acquired OCT image. Image (b) includes the correction for the nonlinear delay of the axial scanner. Image (c) further includes the correction of the divergent scan geometry due to telecentric scanning. Image (d) corrects for the refraction at the air–cornea and endothelium–aqueous boundaries (Images used with permission from [60])
13.5 Motion and Phase
Motion estimation and compensation methods have widespread applicability in imaging modalities including OCT. Numerous OCT modalities such as Doppler OCT [66], speckle variance imaging [67], optical micro angiography (OMAG) [68], optical coherence elastography (OCE) [69], and magnetomotive OCT (MM-OCT) [70] explicitly rely on motion for estimating the flow and viscoelastic properties of the specimen. Motion artifacts arising from physiological fluctuations such as heart beat and respiration and involuntary movement of a living subject, in addition to fluctuations caused by a noisy environment and galvanometer jitter, can be detrimental to these imaging modalities. Motion artifacts can not only degrade image quality but also limit the accuracy and reproducibility of quantitative measurements in OCT [71]. Motion artifacts arise when the sample moves during data acquisition and the OCT image reconstruction process assumes the sample to be stationary. High-speed data acquisition can mitigate the impact of motion artifacts to some extent; however, acquiring OCT volumes for a large field-of-view still takes a few seconds, and motion compensation algorithms need to be applied in post-processing to minimize the impact of motion artifacts.
Techniques based on the cross-correlation have been widely used for motion compensation and estimation. These methods are primarily based on finding the shifts corresponding to the maximum cross-correlation values. It is usually helpful to upsample the data prior to finding the cross-correlation values to detect sub-pixel shifts. Cross-correlations between successive A-scans have been used to correct for axial motion [72], while others used cross-correlations between orthogonal B-scans to correct for both axial and transverse motion [73]. Similar techniques were used to correct phase fluctuations due to cardiac and respiratory motions [74]. Some of the more recent methods include optimizing a set of objective functions for image registration [75]. Histogram-based bulk motion estimation methods have been applied to phase-resolved techniques such as Doppler OCT and optical angiography. In these methods, the phase differences between two adjacent A-scans are calculated and the bulk motion is estimated based on the phase difference corresponding to the mode of histogram distribution of these phase differences. This phase difference is then subtracted from the second A-scan to compensate for motion artifacts [76]. Motion compensation techniques have also been used for OCT image formation while manually scanning a probe over a sample. By measuring the de-correlation of the adjacent A-scans, the velocity of the movement of the probe can be measured and used to correct for motion artifacts due to nonuniform scanning [77, 78].
Sub-wavelength motion can induce a phase change in the measured OCT signal. With the advancement of phase-stable Fourier-based systems, techniques have been developed to estimate the phase values and infer a displacement. Furthermore, based on these phase measurements, some authors use a finite difference (numerical derivative) approach to solve the velocity or acceleration. Some authors use this approach combined with cross-correlation to improve sensitivity of the OCT system [79]. One study used the group velocity and phase of a common scatterer to stabilize the system before solving the inverse problem of interferometric synthetic aperture microscopy (ISAM) [80]. Figure 13.9 shows an example where phase correction was applied using a coverslip as a phase reference. Another study performed Doppler flow imaging of cytoplasmic streaming using a common path interferometer [81]. One study developed a magnetomotive optical coherence elastography approach to detect the elastic moduli of a medium by detecting the position and displacement of nanoparticles, which have displacements induced by an external magnetic field that switches on and off [82]. Measuring phase to within a wavelength can be difficult, so some authors use phase unwrapping techniques. One technique in particular involves calculating a synthetic wavelength, longer than the center wavelength, by dividing the spectra into subbands for processing [83].
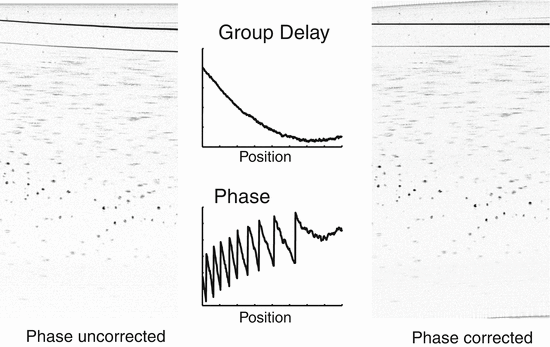

Fig. 13.9




Example of phase correction by using a coverslip placed on the top of the tissue phantom as a phase reference. Phase uncorrected image (left). Image after phase correction (right). Images used with permission from [80]. The plots show the group delay and phase as a function of transverse position on the coverslip interface
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


