(8.1)
where D i is the photocurrent at one detector; k m is the wavenumber; ρ is the detector responsivity; S is the source spectral density in watts per wavenumber; R R and R S are the reflectivity from the reference and sample arm, respectively; and φ i is a trivial phase offset of the interferometric signal. The detector elements are i = 1: M where, in SDOCT, M is the number of pixels of the camera in the spectrometer or, in SSOCT, M is the number of spectral samples over the entire bandwidth of the wavelength-swept laser. The difference in optical path length between the reflectors in the sample and the reference arm is encoded by the frequency of the cosine term, and sample reflectivity is encoded in the fringe visibility of the interferometric signal. The detected signal in FDOCT essentially represents the real part of a Fourier transform of an OCT A-line given by
![$$ {D}_i\left[{x}_m\right]={\displaystyle {\sum}_{m=1}^M}{D}_i\left[{k}_m\right]{e}^{-\left(j2\pi \left(2{k}_m{x}_n\right)\right)},n\in \left\{1,M\right\} $$](/wp-content/uploads/2017/03/A76297_2_En_9_Chapter_Equ2.gif)
(8.2)
In the space domain, the channel spaces are given by 1/Δk where Δk is the bandwidth of the source in wavenumber units. As previously mentioned, the scan depth is given by the spectral resolution of system 1/δk where δk is the spectral resolution. Performing the Fourier transform shown in (8.2), the OCT A-line in the space domain is then represented by the following:
![$$ {D}_i\left[{x}_n\right]\propto S\left[{x}_n\right]\otimes \left(\left({R}_R+{R}_S\right)\delta \left({x}_n\right)+2\sqrt{R_R{R}_S}\left(\delta \left({x}_n+\Delta x\right)+\delta \left({x}_n-\Delta x\right)\right)\right) $$](/wp-content/uploads/2017/03/A76297_2_En_9_Chapter_Equ3.gif)
(8.3)
Because the detected signal is necessarily real, the resulting Fourier transform will result in a Hermitian symmetric A-line, evidenced by the presence of two delta functions offset by +Δx and −Δx from DC. Therefore, a reflector at +Δx cannot be distinguished from a reflector located −Δx. This ambiguity is termed the complex conjugate artifact [26], which effectively reduces the scan depth by a factor 2. Lastly, the DC artifact is given by the first delta function in the brackets.
The typical manner of resolving the complex conjugate artifact is to ensure that the region of interest in the sample is located solely on one side of the zero path length position, given by the position of the reference mirror. Duplicate data from the other side of the zero path length position is simply cropped out. While the majority of FDOCT systems utilize this technique, it is inefficient since half of the collected data is redundant and thus discarded. Complex conjugate removal (CCR) techniques in FDOCT aim to suppress or altogether eliminate this artifact to double imaging range, thereby enabling the entire collected data to be utilized efficiently. Some CCR techniques, such as phase-shifting OCT, are applicable in either SD or SSOCT, while others such as Heterodyne OCT are more suitable for SSOCT, as discussed below. This chapter will focus on CCR in SSOCT, while CCR in SDOCT, which is the focus of Chap. 7, “Optical Frequency Domain Imaging,” will be briefly reviewed.
8.1.2 Complex Conjugate Removal in Spectral Domain OCT
As previously stated, the main drawback of adopting FDOCT is the complex conjugate artifact. Therefore, a major focus of OCT research was on techniques that suppress or eliminate the complex conjugate artifact. The majority of these techniques were developed for SDOCT and will be reviewed here. CCR in SSOCT will be discussed in the following sections.
The complex conjugate artifact originates from the collection of only the real part of the complex OCT signal in FDOCT. However, if the entire complex OCT signal can be collected, then the Fourier transform of the complex signal back to the spatial domain would yield a complex conjugate free A-line. Because optical detectors necessarily acquire real data, reconstructing the complex OCT signal is not trivial. A method of acquiring both the real and imaginary components of the complex OCT signal involves acquiring multiple (at least two) interferograms at the same location but with a relative phase shift – a technique termed phase-shifting OCT. Phase shifting can be done in a variety of ways, including dithering the reference mirror with a piezoelectric transducer (PZT) [26, 27] or incurring a phase shift with an electro-optic modulator [28]. Using a PZT for phase stepping tends to severely hinder imaging speed since the OCT frame rate is now limited by the response time of the PZT. As a consequence, phase stepping with a PZT is more sensitive to patient motion than when using electro-optic modulator.
Once the phase-shifted interferograms are acquired, the complex OCT signal must be reconstructed. The first phase-shifting OCT systems employed a five shifted frame algorithm, first developed for white-light interferometry [29]. Five frames were necessary to correct for chromatic phase error induced by phase shifting using the reference mirror. Once again, collecting five frames sequentially is time consuming, and therefore the algorithm is vulnerable to patient motion that may introduce phase error. Other algorithms have been developed that only necessitate two phase-shifted to reduce imaging time; however, such algorithms are only applicable for limited optical bandwidths [28, 30]. Another group developed a system in which the phase-shifted spectra can be collected on different line arrays of a 2D detector to increase speed of imaging [31]. However, five phase-shifted frames were still necessary for every complex conjugate-resolved B-scan.
In addition to phase shifting, other phase modulation techniques for CCR in SDOCT have been developed. Sinusoidal phase modulation of the reference mirror and a high-speed integrating buckets acquisition scheme has also been utilized for reconstruction of the complex OCT signal [32]. Another algorithm was explored to retrieve the in-phase and quadrature components of the complex OCT signal from the first and second harmonics of the phase-modulated interferogram [33]. Instead of moving the reference arm, phase modulation of the interferogram can also be induced by offsetting the beam away from the pivot of the fast scanning mirrors. This incurs a phase shift that is proportional to the rate of the scanning mirrors and is therefore a simple way in which the complex OCT signal can be reconstructed after phase modulation [34, 35]. Another technique, termed B-M-mode OCT, uses phase modulation of a reference beam while transverse scanning to retrieve the complex OCT signal [36].
A completely different approach utilizes multiple reference arms to circumvent the complex conjugate artifact rather than suppress it. This technique simply uses two reference arms, with the zero path length of each located at different positions in the sample. Therefore, two images, collected from different regions of the sample, can be captured and later registered to produce an image with greater depth range and free of the complex conjugate ambiguity. A fiber-based optical switch can be used to minimize the time it takes to switch between reference arms [37].
Another method to obtain for CCR is applying an electronic carrier frequency to the interferogram using frequency-shifting devices. This method does not induce any chromatic phase shift error, unlike most phase-shifting techniques, and allows for quadrature detection of the OCT signal. Frequency shifting in OCT is termed Heterodyne OCT and is more suitable for SSOCT since spectral domain detectors cannot follow MHz signal modulations. However, frequency shifting has also been applied to SDOCT using acousto-optic frequency shifters [38]. After applying a constant carrier frequency to the spatial OCT interferogram, a Hilbert transform can be used to capture the quadrature components of the OCT signal [39].
There are some disadvantages with the previously discussed methods, which include reduced imaging time since most CCR techniques in SDOCT necessitate the acquisition of multiple, phase-shifted frames or the use of multiple reference arms. Furthermore, phase-stepping or modulation techniques are subject to phase noise incurred by either patient movement or mechanical instability of the system. The accuracy of the complex OCT signal is dependent on the phase stability of the system. That is, for phase-shifting OCT, “phase calibration” is usually required, in which the phase shift between frames is predetermined and chosen carefully for the algorithm to work. Any phase noise will cause deviations from these predetermined phase shifts and therefore cause errors in the reconstruction of the complex FDOCT signal, resulting in “ghost images” because the complex conjugate artifact is not fully suppressed. Furthermore, chromatic phase error is incurred when phase shifting by dithering the reference mirror and can again contribute to ghost images. These phase-shifting techniques described above are more suitable for SDOCT because of greater source phase stability than in SSOCT. A true achromatic method for CCR is heterodyne OCT, in which a frequency carrier is imparted on the interferometric signal. This technique is more suitable for SSOCT since spectral domain detectors cannot follow fast signal modulations in the MHz range.
8.2 Heterodyne SSOCT
A method for true achromatic complex FDOCT signal reconstruction uses frequency shifting devices to create a beating signal with the detected interferometric signal. Termed heterodyne OCT, this technique is especially suitable for SSOCT in which large bandwidth detectors that can capture fast signal modulations in the MHz to 1 GHz range are used. A carrier signal can be imparted to enable quadrature detection of the complex OCT signal and subsequent suppression of the complex conjugate ambiguity. Furthermore, frequency shifting can also be used to establish a new zero optical path delay and eliminate the complex conjugate ambiguity altogether.
8.2.1 Heterodyne SSOCT Theory
As stated previously, the photocurrent collected by the detectors can be expressed as (8.1). In the case for SSOCT, the wavenumber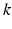 
is swept as a function of time and can be represented as k = k 0 + t(dk/dt) where k 0 is the starting wavenumber in the sweep and dk/dt is the instantaneous sweep velocity. Optical sweeping in the time domain leads to the conversion of the cross-correlation and autocorrelation to electronic frequency in the time-varying photocurrent D[t]. Note that in Eq. 8.1, photocurrent is expressed as a function of k. However, since wavenumber is swept as function of time in SSOCT, photocurrent can be recast in terms of t.
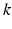is swept as a function of time and can be represented as k = k 0 + t(dk/dt) where k 0 is the starting wavenumber in the sweep and dk/dt is the instantaneous sweep velocity. Optical sweeping in the time domain leads to the conversion of the cross-correlation and autocorrelation to electronic frequency in the time-varying photocurrent D[t]. Note that in Eq. 8.1, photocurrent is expressed as a function of k. However, since wavenumber is swept as function of time in SSOCT, photocurrent can be recast in terms of t.The cross-correlation frequencies can be represented by the multiplication of OPL mismatch between the sample and reference arm and the sweep velocity ω n = (dk/dt) (z R − z n ), while the autocorrelation frequencies are given by ω nm = (dk/dt) (z n − z m ). If a beat frequency ω d is induced in the reference arm, then the time-varying photocurrent can be represented by
![$$ {D}_i\left[t\right]\propto \rho \cdot S\left[t\right]\cdot \left\{{R}_R+{\displaystyle {\sum}_n}{R}_n+2\sqrt{R_R}{\displaystyle {\sum}_n}\sqrt{R_n} \cos \left[\left({\omega}_n+{\omega}_D\right)t+{\varphi}_n\right]+2{\displaystyle {\sum}_n}{\displaystyle {\sum}_{m\ne n}}\sqrt{\left({R}_n{R}_m\right)} \cos \left({\omega}_{nm}t+{\varphi}_{nm}\right)\right\} $$](/wp-content/uploads/2017/03/A76297_2_En_9_Chapter_Equ4.gif)
where φ n and φ nm are trivial initial phase offsets. As evident in the equation, the autocorrelation artifacts, given by the last term inside the brackets, are still centered around the baseband, while the cross-correlation terms, given by the third term inside the brackets, are now shifted away from DC and centered around the carrier frequency ω D . Although the Fourier transform of the frequency-shifted signal is still Hermitian symmetric, the frequency-shifted fringes are far away enough from baseband such that negative and positive displacements can be differentiated. Positive displacements are located above ω D , while negative displacements are below ω D but above the baseband, as long as ω D is higher than the highest frequency signal, i.e., the maximum ω n .
(8.4)
A frequency shift of ω D corresponds to a path length shift of z D , where z D = ω D Δt/(2Δk) where Δt is the time it takes for the source to sweep over the entire bandwidth and Δk is the bandwidth of the source in wavenumber units. This shift in frequency is not subject to conventional FDOCT signal falloff, governed by the spectral source instantaneous linewidth in SSOCT. Instead, the frequency shift merely creates a time-varying beat frequency that is not dependent on source linewidth or source sweep rate.
8.2.2 Heterodyne OCT with Frequency-Shifting Devices
There are several algorithms in heterodyne OCT to recover a complex conjugate-free image. The first to be discussed, implemented by Davis et al. [40], utilized a band-pass filter around the carrier frequency and subsequent demodulation to recover the inphase and quadrature components of the complex OCT signal. The optical setup, depicted in Fig. 8.1, employed two acousto-optic modulators centered at 100 MHz, with a user tunable offset frequency in one modulator to provide the carrier frequency. Circulators were used to minimize the amount of optical power loss through the AOMs. Wavenumber triggering was used to remap the sweep linearly in wavenumber.
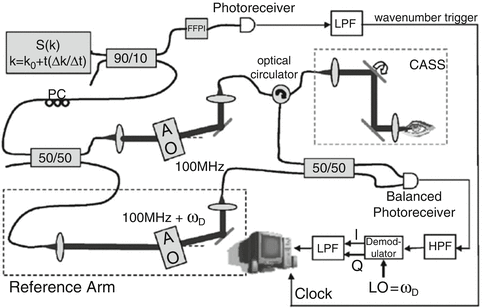
Fig. 8.1
Heterodyne SSOCT system using AOMs to frequency upshift interferogram. The swept laser was centered at 1,300 nm with a bandwidth of 100 nm. Balanced detection is used for common noise rejection. AO acousto-optic modulator, PC polarization controller, FFPI Fabry-Perot interferometer, CASS corneal anterior segment scanner
After the heterodyned interferometric signal was collected, a high-pass filter was used to remove the DC and autocorrelation artifacts. The filtered signal is then demodulated by mixing with a local oscillator of the same frequency as the carrier frequency. The in-phase and quadrature components can then be recovered to reconstruct the complex OCT signal. Furthermore, after demodulation, the resulting signal is only dependent on ω n ; therefore, conventional wavenumber triggering can be used to remap the sweep linearly in time. Figure 8.2 depicts captured interferometric fringes with and without the frequency shift. Two different interferograms are analyzed, with frequencies corresponding to reflectors at +/−50 μm displacements. As evident, with no frequency shift, the interferograms cannot be differentiated due to the complex conjugate ambiguity. However, collection of the same exact reflectors but with a carrier frequency of 20 kHz depicts how the two interferograms are now at different frequencies and can be easily differentiated. The fringe frequency for the positive displacement is greater than the fringe frequency for the negative displacement.
Fig. 8.2
Interferograms captured from reflectors at +/−50 μm displacements using homodyne and heterodyne SSOCT. The top row illustrates the homodyne case, while the bottom row illustrates the effect of frequency shifting by 20 kHz. As evident, the two reflectors in the homodyne case are indistinguishable, while the reflector at the positive displacement has much higher frequency fringes than the reflector at the negative displacement. Notice that the frequency-shifted signals are chirped, indicating that the signal must first be demodulated before wavenumber triggering
As previously mentioned, frequency shifting not only resolves the complex conjugate ambiguity but also eliminates the DC and autocorrelation artifacts. The anterior segment of the eye was imaged using heterodyne SSOCT to illustrate the utility of frequency shifting. The power on the eye was 60 μm and the images were constructed using 500 lines/image acquired at 250 Hz. With homodyne SSOCT, the entire anterior segment cannot be visualized simultaneously; however, frequency shifting doubles the imaging depth range and enables simultaneous imaging of the cornea, sclera, and iris, as shown in Fig. 8.3.
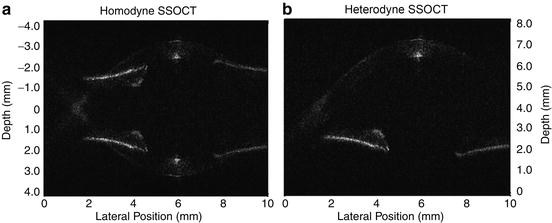
Fig. 8.3
In vivo images of the anterior segment of a human eye with homodyne (a) and heterodyne (b) SSOCT. The complex conjugate artifacts are resolved in the heterodyne case, doubling depth imaging range to about 8 mm and enabling visualization of the entire anterior segment
Zhang et al. utilized an electro-optic phase modulator (EOM) to induce a carrier frequency, similar to the frequency-shifting process described above [41, 42]. To compensate for group-velocity dispersion mismatch induced by the EOM, a rapid scanning optical delay line was used. The upshifted signal was band-pass filtered and demodulated to retrieve the complex OCT signal and resolve the complex conjugate ambiguity. As mentioned before, the demodulation of the frequency-shifted signal before remapping the source sweep linearly in wavenumber is necessary to avoid chirping. Furthermore, removal of low-frequency noise as well as autocorrelation artifacts improved system sensitivity by 20 dB. As with the previous technique, removal of the complex conjugate artifact resulted in an increased imaging range by a factor of 2 and was demonstrated by imaging rabbit cornea. Figure 8.4 illustrates the ability to image the entire corneal depth after removal of the complex conjugate artifact.
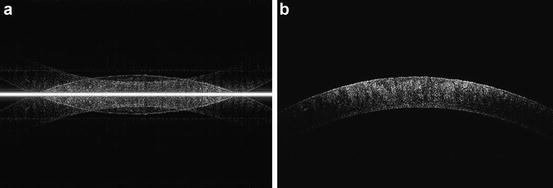
Fig. 8.4
Images of rabbit cornea obtained without (a) and with (b) the EOM. As evident, frequency upshifting results in a doubling of imaging depth range. The entire corneal curvature can be imaged only after removal of the complex conjugate ambiguity
Another group demonstrated CCR with AOMs, similar to Davis et al. As before, a carrier frequency was applied to electronically shift interferometric signal away from baseband. However, unlike the previously discussed techniques, IQ demodulation was not performed, and the interferometric signal at the carrier frequency was digitized and processed. Instead of performing IQ demodulation to reconstruct the complex OCT signal, the authors relied on the frequency shift induced by the AOMs to be far away enough from baseband such that the negative path length differences are still above DC. A Fourier transform of this signal is still Hermitian symmetric; however, the complex conjugate ambiguity is still resolved since the entire imaging range is located above baseband. Therefore, as long as a digitizer and photoreceiver with large enough bandwidths are utilized, the upshifted interferometric signal can be collected directly, resulting in a complex conjugate free A-line. Figure 8.5 illustrates this concept. As shown, the zero path delay is now upshifted to some carrier frequency, resulting in locating the entire coherence range on the positive frequency side of DC, doubling the effective ranging depth [43].
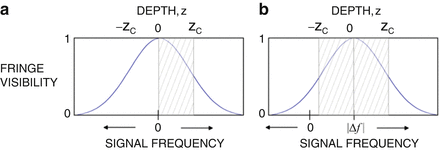
Fig. 8.5
Plot of fringe visibility versus fringe signal frequency without (a) and with (b) frequency shifting. Frequency shifting enables both sides of the coherence range to be utilized, therefore doubling the imaging range. Negative and positive path lengths are readily differentiated after frequency shifting
CCR was demonstrated on ex vivo images of human lung tissue. A −2.5 MHz frequency shift, corresponding to a 2.9 mm path length shift, was induced using AOMs. The upshifted interferogram was captured and digitized without any demodulation. Therefore, the zero path length position in the heterodyne OCT image is now located 2.9 mm deeper relative to the homodyne OCT image, effectively doubling the imaging range, as shown in Fig. 8.6.
Fig. 8.6
Heterodyne (right) and homodyne (left) OCT ex vivo images of human lung tissue. The frequency shift of −2.5 MHz corresponds to a path length shift of 2.9 mm. The frequency-shifted image results in doubling of the depth range
8.2.3 Heterodyne OCT with Coherence Revival
Coherence revival refers to observing interference fringes in an interferometer not only when the sample and reference arms OPLs are matched but also when the OPL mismatch is an integer multiple of the cavity length of the source [44]. This phenomenon can occur if the laser oscillates at multiple longitudinal modes simultaneously; if so, then the multimode field emitted exhibits periodicity. The period at which the interference fringes are seen is equal to the reciprocal of the mode space or alternatively equal to the round-trip optical delay of the cavity length. Therefore, by inserting a “virtual” cavity in either the sample or reference arm by mismatching the OPL difference by an integer multiple of the cavity length, interference fringes are still observed. This phenomenon is present in some external cavity lasers used in SSOCT.
Of particular importance is frequency shifting in coherence revival. For the two swept-source lasers investigated in [45], inserting a virtual cavity also results in phase modulation of the interferometric fringes seen in coherence revival. This phase modulation results in a frequency upshift, equivalent to imparting a carrier frequency with AOMs, as described above. Therefore, phase modulation in coherence revival enables CCR by the same principles as frequency upshifting with AOMs. Although the exact origin of the phase modulation in coherence revival is unknown, it is suggested that a change in the physical length of the cavity or a modulation of the refractive index of the gain media may be responsible [46]. Nevertheless, coherence revival heterodyne OCT behaves exactly the same as the previous heterodyne OCT methods, except that it does not require a frequency-shifting device such as an AOM.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
