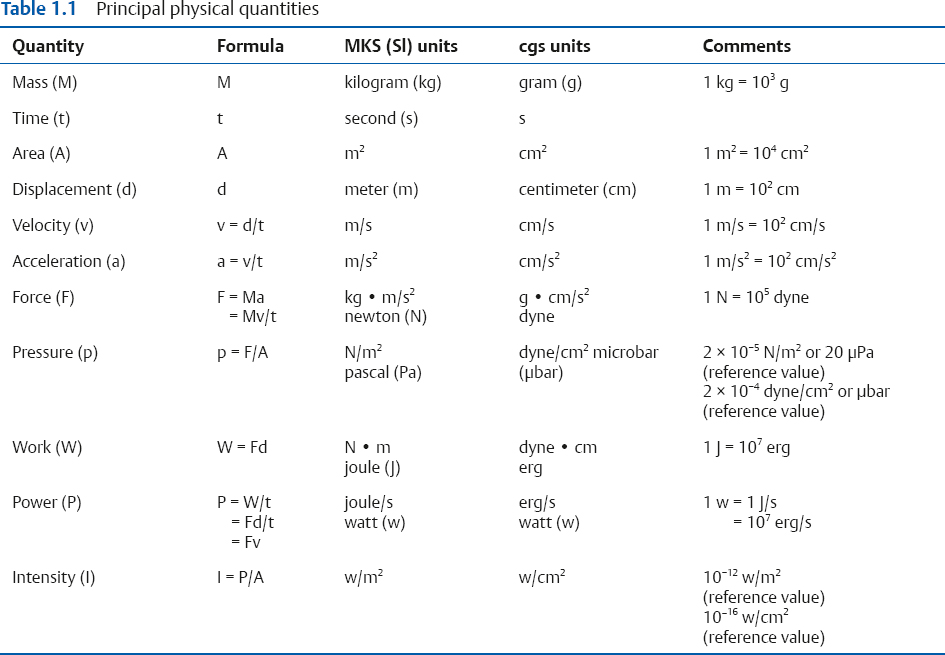
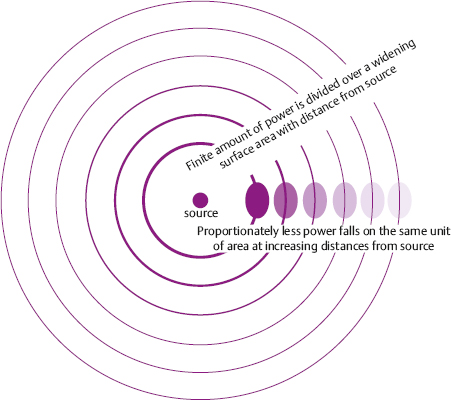
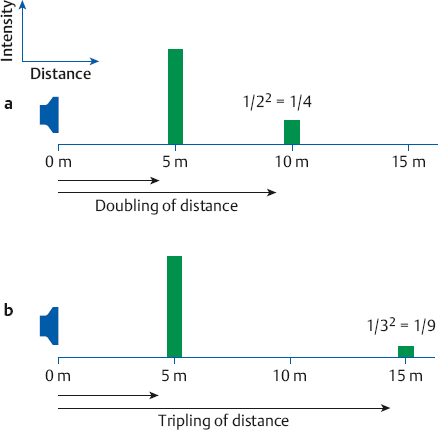
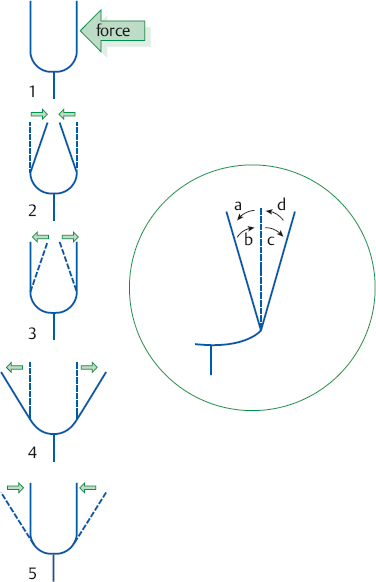
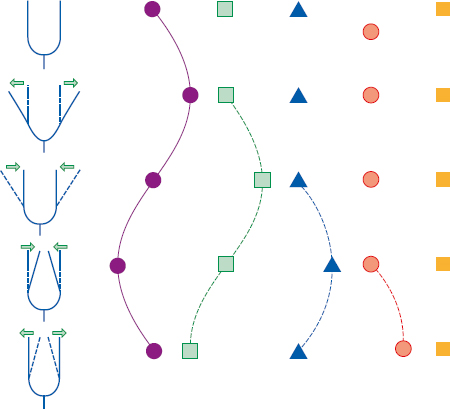
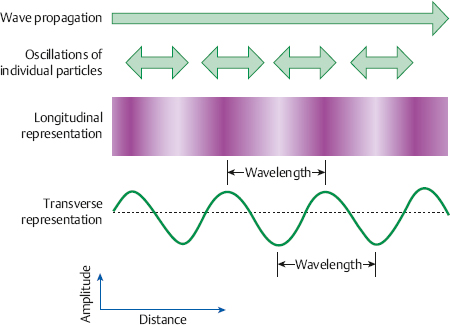
1 Acoustics and Sound Measurement We begin our study of audiology by reviewing the nature of sound because, after all, sound is what we hear. The science of sound is called acoustics, which is a branch of physics, and relies on several basic physical principles. Many useful sources are available for students wishing to pursue the areas covered in this chapter in greater detail (e.g., Beranek 1986; Gelfand 2010; Hewitt 1974; Kinsler, Frey, Coppens, & Sanders 1982; Peterson & Gross 1972; Sears, Zemansky, & Young 1982). The basic physical quantities are mass, time, and length (or distance). All other physical quantities are derived by combining these three basic ones, as well as other derived quantities, in a variety of ways. The principal basic and derived quantities are summarized in Table 1.1. These basic quantities are expressed in terms of conventional units that are measurable and repeatable. The unit of mass (M) is the kilogram (kg) or the gram (g); the unit of length (L) is the meter (m) or the centimeter (cm); and the unit of time (t) is the second (s). Mass is not really synonymous with weight even though we express its magnitude in kilograms. The mass of a body is related to its density, but its weight is related to the force of gravity. If two objects are the same size, the one with greater density will weigh more. However, even though an object’s mass would be identical on the earth and the moon, it would weigh less on the moon, where there is less gravity. When we express mass in kilograms and length in meters, we are using the meter–kilogram-second or MKS system. Expressing mass in grams and length in centimeters constitutes the centimeter-gram-second or cgs system. These two systems also have different derived quantities. For example, the units of force and work are called newtons and joules in the MKS system, and dynes and ergs in the cgs system, respectively. We will emphasize the use of MKS units because this is the internationally accepted standard in the scientific community, known as the Systeme Internationale (SI). Equivalent cgs values will often be given as well because the audiology profession has traditionally worked in cgs units, and the death of old habits is slow and labored. These quantities are summarized with equivalent values in MKS and cgs units in Table 1.1. In addition, the correspondence between scientific notation and conventional numbers, and the meanings of prefixes used to describe the sizes of metric units are shown for convenience and ready reference in Table 1.2 and Table 1.3. Quantities may be scalars or vectors. A scalar can be fully described by its magnitude (amount or size), but a vector has both direction and magnitude. For example, length is a scalar because an object that is one meter long is always one meter long. However, we are dealing with a vector when we measure the distance between two coins that are one meter apart because their relationship has both magnitude and direction (from point x1 to point x2). This quantity is called displacement (d). Derived quantities will be vectors if they have one or more components that are vectors; for example, velocity is a vector because it is derived from displacement, and acceleration is a vector because it involves velocity. We distinguish between scalars and vectors because they are handled differently when calculations are being made. Velocity Everyone knows that “55 miles per hour” refers to the speed of a car that causes it to travel a distance of 55 miles in a one-hour period of time. This is an example of velocity (v), which is equal to the amount of displacement (d) that occurs over time (t): Displacement is measured in meters and time is measured in seconds (sec); thus, velocity is expressed in meters per second (m/s). Velocity is the vector equivalent of speed because it is based on displacement, which has both magnitude and direction. When we take a trip we usually figure out the distance traveled by making a mental note of the starting odometer reading and then subtracting it from the odometer reading at the destination (e.g., if we start at 10,422 miles and arrive at 10,443 miles, then the distance must have been 10,443 – 10,422 = 21 miles). We do the same thing to calculate the time it took to make the trip (e.g., if we left at 1:30 and arrived at 2:10, then the trip must have taken 2:10 – 1:30 = 40 minutes). Physical calculations involve the same straightforward approach. When an object is displaced, it starts at point x1 and time t1 and arrives at point x2 and time t2. Its average velocity is simply the distance traveled (x2 – x1) divided by the time it took to make the trip (t2 – t1): The term instantaneous velocity describes the velocity of a body at a particular moment in time. For the math-minded, it refers to the velocity when the displacement and time between one point and the next one approach zero, that is, the derivative of displacement with respect to time: Acceleration Driving experience has taught us all that a car increases its speed to get onto a highway, slows down when exiting, and also slows down while making a turn. “Speeding up” and “slowing down” mean that the velocity is changing over time. The change of velocity over time is acceleration (a). Suppose a body is moving between two points. Its velocity at the first point is v1, and the time at that point is t1. Similarly, its velocity at the second point is v2 and the time at that point is t2. Average acceleration is the difference between the two velocities (v2 – v1) divided by the time interval (t2 – t1): In more general terms, acceleration is written simply as Because velocity is the same as displacement divided by time, we can replace v with d/t, so that which can be simplified to Consequently, acceleration is expressed in units of meters per second squared (m/s2) in the MKS system. When measurements are made in cgs units, acceleration is expressed in centimeters per second squared (cm/s2). Acceleration at a given moment is called instantaneous acceleration, and quantitatively oriented readers should note it is equal to the derivative of velocity with respect to time, or Force An object that is sitting still will not move unless some outside influence causes it to do so, and an object that is moving will continue moving at the same speed unless some outside influence does something to change it. This commonsense statement is Newton’s first law of motion. It describes the attribute of inertia, which is the property of mass to continue doing what it is already doing. The “outside influence” that makes a stationary object move, or causes a moving object to change its speed or direction, is called force (F). Notice that force causes the moving object to change velocity or the motionless object to move, which is also a change in velocity (from zero to some amount). Recall that a change of velocity is acceleration. Hence, force is that influence (conceptually a “push” or “pull”) that causes a mass to be accelerated. In effect, the amount of “push” or “pull” needed depends on how much mass you want to influence and the amount of acceleration you are trying to produce. In other words, force is equal to the product of mass times acceleration: F = Ma Since acceleration is velocity over time (v/t), we can also specify force in the form The quantity Mv is called momentum, so we may also say that force equals momentum over time. The amount of force is measured in kg · m/s2 because force is equal to the product of mass (measured in kg) and acceleration (measured in m/s2). The unit of force is the newton (N), where one newton is the amount of force needed to cause a 1 kg mass to be accelerated by 1 m/s2; hence, 1 N = 1 kg · 1 m/s2. (This might seem very technical, but it really simplifies matters; after all, it is easier to say “one newton” than “one kg · m/s2.”). It would take a 2 N force to cause a 1 kg mass to be accelerated by 2 m/s2, or a 2 kg mass to be accelerated by 1 m/s2. A 4 N force is needed to accelerate a 2 kg mass by 2 m/s2, and a 63 N force is needed to accelerate a 9 kg mass by 7 m/s2. In the cgs system, the unit of force is called the dyne, which is the force needed to accelerate a 1 g mass by 1 cm/s2; that is, 1 dyne = 1 g · cm/s2. It takes 105 dynes to equal 1 N. Many different forces are usually acting upon an object at the same time. Hence, the force we have been referring to so far is actually the net or resultant force, that is, the “bottom line” effect of all the forces that act upon an object. If a force of 3 N is pushing an object toward the right and a second force of 8 N is also pushing that object toward the right, then the net force would be 3 + 8 = 11 N toward the right. In other words, if two forces push a body in the same direction, then the net force would be the sum of those two forces. Conversely, if a 4 N force pushes an object toward the right at the same time that a 9 N force pushes it toward the left, then the net force is 9 – 4 = 5 N toward the left. Thus, if two forces push an object in opposite directions, then the net force is the difference between the two opposing forces, and it causes the object to accelerate in the direction of the greater force. If two equal forces push in opposite directions, then the net force is zero. Because the net force is zero it will not cause the motion of the object to change. The situation in which net force is zero is called equilibrium. In this case, a moving object will continue moving and an object that is at rest (i.e., not moving) will continue to remain still. Friction When an object is moving in the real world, it tends to slow down and eventually comes to a halt. This happens because anything that is moving in the real world is always in contact with other bodies or mediums. The sliding of one body on the other constitutes a force that opposes the motion, called resistance or friction. The opposing force of friction or resistance depends on two parameters. The first factor is that the amount of friction depends on the nature of the materials that are sliding on one another. Simply stated, the amount of friction between two given objects is greater for “rough” materials than for “smooth” or “slick” ones, and is expressed as a quantity called the coefficient of friction. The second factor that determines how much friction occurs is easily appreciated by rubbing the palms of your hands back and forth on each other. First rub slowly and then more rapidly. The rubbing will produce heat, which occurs because friction causes some of the mechanical energy to be converted into heat. This notion will be revisited later, but for now we will use the amount of heat as an indicator of the amount of resistance. Your hands become hotter when they are rubbed together more quickly. This illustrates the notion that the amount of friction depends on the velocity of motion. In quantitative terms, F = Rv where F is the force of friction, R is the coefficient of friction between the materials, and v is the velocity of the motion. We know from common experiences, such as using simple exercise equipment, that it is relatively easy to begin compressing a spring (e.g., a “grip exerciser”), but that it gets progressively harder to continue compressing it. Similarly, it is easier to begin expanding a spring (e.g., pulling apart the springs on a “chest exerciser”) than it is to continue expanding it. In other words, the more a spring-like material (an elastic element) is deformed, the more it opposes the applied force. The force that opposes the deformation of an elastic or spring-like material is known as the restoring force. If we think of deformation in terms of how far the spring has been compressed or expanded from its original position, we could also say that the restoring force increases with displacement. Quantitatively, then, restoring force (FR) depends on the stiffness (S) of the material and the amount of its displacement as follows: FR = Sd Pressure Very few people can push a straight pin into a piece of wood, yet almost anyone can push a thumbtack into the same piece of wood. This is possible because a thumbtack is really a simple machine that concentrates the amount of force being exerted over a larger area (the head) down to a very tiny area (the point). In other words, force is affected by the size of the area over which it is applied in a way that constitutes a new quantity. This quantity, which is equal to force divided by area (A), is called pressure (p), so Because force is measured in newtons and area is measured in square meters in MKS units, pressure is measured in newtons per square meter (N/m2). The unit of pressure is the Pascal (Pa), so that 1 Pa = 1 N/m2. In the cgs system, pressure is measured in dynes per square centimeter (dynes/cm2), occasionally referred to as microbars (μbars). Work and energy As a physical concept, work (W) occurs when the force applied to a body results in its displacement, and the amount of work is equal to the product of the force and the displacement, or W = Fd Because force is measured in newtons and displacement is measured in meters, work itself is quantified in newton-meters (N · m). For example, if a force of 2 N displaces a body by 3 m, then the amount of work is 2 × 3 = 6 N. There can only be work if there is displacement. There cannot be work if there is no displacement (i.e., if d = 0) because work is the product of force and displacement, and zero times anything is zero. The MKS unit of work is the joule (J). One joule is the amount of work that occurs when one newton of force effects one meter of displacement, or 1 J = 1 N · m. In the cgs system, the unit of work is called the erg, where 1 erg = 1 dyne · cm. One joule corresponds to 107 ergs. Energy is usually defined as the capability to do work. The energy of a body at rest is potential energy and the energy of an object that is in motion is kinetic energy. The total energy of a body is the sum of its potential energy plus its kinetic energy, and work corresponds to the exchange between these two forms of energy. In other words, energy is not consumed when work is accomplished; it is converted from one form to the other. This principle is illustrated by the simple example of a swinging pendulum. The pendulum’s potential energy is greatest when it reaches the extreme of its swing, where its motion is momentarily zero. On the other hand, the pendulum’s kinetic energy is greatest when it passes through the midpoint of its swing because this is where it is moving the fastest. Between these two extremes, energy is being converted from potential to kinetic as the pendulum speeds up (on each down swing), and from kinetic to potential as the pendulum slows down (on each up swing). Power The rate at which work is done is called power (P), so that power can be defined as work divided by time, The unit of power is called the watt (w). One unit of power corresponds to one unit of work divided by one unit of time. Hence, one watt is equal to one joule divided by one second, or 1 w = 1 J/s. Power is also expressed in watts in the cgs system, where work is measured in ergs. Since 1 J = 107 erg, we can also say that 1 w = 107 erg/s. Power can also be expressed in other terms. For example, because W = Fd, we can substitute Fd for W in the power formula, to arrive at We know that v = d/t, so we can substitute v for d/t and rewrite this formula as P = Fv In other words, power is also equal to force times velocity. Intensity Consider a hypothetical demonstration in which one tablespoonful of oil is placed on the surface of a still pond. At that instant the entire amount of oil will occupy the space of a tablespoon. As time passes, the oil spreads out over an expanding area on the surface of the pond, and it therefore also thins out so that much less than all the oil will occupy the space of a tablespoon. The wider the oil spreads the more it thins out, and the proportion of the oil covering any given area gets smaller and smaller, even though the total amount of oil is the same. Clearly, there is a difference between the amount of oil, per se, and the concentration of the oil as it is distributed across (i.e., divided by) the surface area of the pond. An analogous phenomenon occurs with sound. It is common knowledge that sound radiates outward in every direction from its source, constituting a sphere that gets bigger and bigger with increasing distance from the source, as illustrated by the concentric circles in Fig. 1.1. Let us imagine that the sound source is a tiny pulsating object (at the center of the concentric circles in the figure), and that it produces a finite amount of power, analogous to the fixed amount of oil in the prior example. Consequently, the sound power will be divided over the ever-expanding surface as distance increases from the source, analogous to the thinning out of the widening oil slick. This notion is represented in the figure by the thinning of the lines at greater distances from the source. Suppose we measure how much power registers on a certain fixed amount of surface area (e.g., a square inch). As a result, a progressively smaller proportion of the original power falls onto a square inch as the distance from the source increases, represented in the figure by the lighter shading of the same-size ovals at increasing distances from the source. The examples just described reveal that a new quantity, called intensity (I), develops when power is distributed over area. Specifically, intensity is equal to power per unit area, or power divided by area, or Fig. 1.1 Intensity (power divided by area) decreases with distance from the sound source because a fixed amount of power is spread over an increasing area, represented by the thinning of the lines. Proportionately less power falls on the same unit area (represented by the lighter shading of the ovals) with increasing distance from the source. Because power is measured in watts and area is measured in square meters in the MKS system, intensity is expressed in watts per square meter (w/m2). Intensity is expressed in watts per square centimeter (w/cm2) in the cgs system. Intensity decreases with increasing distance from a sound source according to a rule called the inverse square law. It states that the amount of intensity drops by 1 over the square of the change in distance. Two examples are illustrated in Fig. 1.2. Frame a shows that when the distance from a loudspeaker is doubled from 5 m to 10 m, the amount of intensity at 10 m will be one quarter of what it was at 5 m (because 1/22 = 1/4). Similarly, frame b shows that tripling the distance from 5 m to 15 m causes the intensity to fall to one ninth of its value at the closer point because 1/32 = 1/9. An important relationship to be aware of is that power is equal to pressure squared, P = p2 Fig. 1.2 Illustrations of the inverse square law. (a) Doubling of distance: The intensity at 10 m away from a loudspeaker is one quarter of its intensity at 5 m because 1/22 = 1/4. (b) Tripling of distance: The intensity at 15 m away from the sources is one ninth of its intensity at 5 m because 1/32 = 1/9. and pressure is equal to the square root of power, In addition, intensity is proportional to pressure squared, and pressure is proportional to the square root of intensity, This simple relationship makes it easy to convert between sound intensity and sound pressure. Sound is often defined as a form of vibration that propagates through the air in the form of a wave. Vibration is nothing more than the to-and-fro motion (oscillation) of an object. Some examples include a playground swing, a pendulum, the floor-boards under a washing machine, a guitar string, a tuning fork prong, and air molecules. The vibration is usually called sound when it is transferred from air particle to air particle (we will see how this happens later). The vibration of air particles might have a simple pattern such as the tone produced by a tuning fork, or a very complex pattern such as the din heard in a school cafeteria. Most naturally occurring sounds are very complex, but the easiest way to understand sound is to concentrate on the simplest ones. A vibrating tuning fork is illustrated in Fig. 1.3. The initial force that was applied by striking the tuning fork is represented by the green arrow in frame 1. The progression of the drawings represents the motion of the prongs at selected points in time after the fork has been activated. The two prongs vibrate as mirror images of each other, so that we can describe what is happening in terms of just one prong. The insert highlights the motion of the right prong. Here the center position is where the prong would be at rest. When the fork is struck the prong is forced inward as shown by arrow a. After reaching the leftmost position it bounces back (arrow b), accelerating along the way. The rapidly moving prong overshoots the center and continues rightward (arrow c). It slows down along the way until it stops for an instant at the extreme right, where it reverses direction again and starts moving toward the left (arrow d) at an ever-increasing speed. It overshoots the center again, and as before, the prong now follows arrow a, slowing down until it stops momentarily at the extreme left. Here it reverses direction again and repeats the same process over and over again. One complete round trip (or replication) of an oscillating motion is called a cycle. The number of cycles that occur in one second is called frequency. This form of motion occurs when a force is applied to an object having the properties of inertia and elasticity. Due to its elasticity, the deformation of the fork caused by the applied force is opposed by a restoring force. In the figure the initial leftward force is opposed by a restoring force in the opposite direction, that is, toward the right. The rightward restoring force increases as the prong is pushed progressively toward the left. As a result, the movement of the prong slows down and eventually stops. Under the influence of its elasticity the prong now reverses direction and starts moving rightward. As the restoring force brings the prong back toward the center, we must also consider its mass. Because the prong has mass, inertia causes it to accelerate as it moves back toward its center resting position. In fact, the prong is moving at its maximum speed as it passes through the resting position. The force of inertia causes the prong to overshoot the center and continue moving rightward. The deformation process begins again once the prong overshoots its resting position. As a result, opposing elastic restoring forces start building up again, now in the leftward direction. Just as before, the increasing (leftward) restoring force eventually overcomes the rightward inertial force, thereby stopping the prong’s displacement at the rightmost point, and causing a reversal in the direction of its movement. Hence, the same course of events is repeated again, this time in the leftward direction; then rightward, then leftward, etc., over and over again. This kind of vibration is called simple harmonic motion (SHM) because the oscillations repeat themselves at the same rate over and over again. Fig. 1.3 After being struck, a tuning fork vibrates or oscillates with a simple pattern that repeats itself over time. One replication (cycle) of this motion is illustrated going from frames 1 to 5. The arrows in the insert highlight the motion of one of the prongs. We know from experience that the oscillations just described do not continue forever. Instead, they dissipate over time and eventually die out completely. The dying out of vibrations over time is called damping, and it occurs due to resistance or friction. Resistance occurs because the vibrating prong is always in contact with the surrounding air. As a result, there will be friction between the oscillating metal and the surrounding air molecules. This friction causes some of the mechanical energy that has been supporting the motion of the tuning fork to be converted into heat. In turn, the energy that has been converted into heat is no longer available to maintain the vibration of the tuning fork. Consequently, the sizes of the oscillations dissipate and eventually die out altogether. A diagram summarizing the concepts just described is shown in Fig. 1.4. The curve in the figure represents the tuning fork’s motion. The amount of displacement of the tuning fork prong around its resting (or center) position is represented by distance above and below the horizontal line. These events are occurring over time, which is represented by horizontal distance (from left to right). The initial displacement of the prong due to the original applied force is represented by the dotted segment of the curve. Inertial forces due to the prong’s mass and elastic restoring forces due to the elasticity of the prong are represented by labeled arrows. Damping of the oscillations due to friction is shown by the decline in the displacement of the curve as time goes on. The curve in this diagram is an example of a waveform, which is a graph that shows displacement (or another measure of magnitude) as a function of time. Tuning fork vibrations produce sound because the oscillations of the prongs are transmitted to the surrounding air particles. When the tuning fork prong moves to the right, it displaces air molecules to its right in the same direction. These molecules are thus displaced to the right of their own resting positions. Displacing air molecules toward the right pushes them closer to the air particles to their right. The pressure that exists among air molecules that are not being disturbed by a driving force (like the tuning fork) is known as ambient or atmospheric pressure. We can say that the rightward motion of the tuning fork prong exerts a force on the air molecules that pushes them together relative to their undisturbed, resting situation. In other words, forcing the air molecules together causes an increase in air pressure relative to the ambient pressure that existed among the undisturbed molecules. This state of positive air pressure is called compression. The amount of compression increases as the prong continues displacing the air molecules rightward. A maximum amount of positive pressure occurs when the prong and air molecules reach their greatest rightward displacement. Fig. 1.4 Diagrammatic representation of tuning fork oscillations over time. Vertical displacement represents the amount of the tuning fork prong displacement around its resting position. Distance from left to right represents the progression of time. (From Gelfand 2010, courtesy of Informa.) The tuning fork prong then reverses direction, overshoots its resting position, and proceeds to its leftmost position. The compressed air molecules reverse direction along with the prong. This occurs because air is an elastic medium, so the particles compressed to the right develop a leftward restoring force. Small as they are, air particles do have mass. Therefore, inertia causes the rebounding air particles to overshoot their resting positions and to continue toward their extreme leftward positions. As the particles move leftward, the amount of compression decreases and is momentarily zero as they pass through their resting positions. As they continue to move to the left of their resting positions, the particles are now becoming increasingly farther from the molecules to their right (compared with when they are in their resting positions). We now say that the air particles are rarefied compared with their resting states, so that the air pressure is now below atmospheric pressure. This state of lower than ambient pressure is called rarefaction. When the air particles reach the leftmost position they are maximally rarefied, which means that the pressure is maximally negative. At this point, the restoring force instigates a rightward movement of the air molecules. This movement is enhanced by the push of the tuning fork prongs that have also reversed direction. The air molecules now accelerate rightward (so that the amount of rarefaction decreases), overshoot their resting positions, and continue to the right, and so on. The tuning fork vibrations have now been transmitted to the surrounding particles, which are now also oscillating in simple harmonic motion. Sounds that are associated with simple harmonic motion are called pure tones. Let us consider one of the air molecules that has already been set into harmonic motion by the tuning fork. This air particle now vibrates to-and-fro in the same direction that was originally imposed by the vibrating prong. When this particle moves toward its right it will cause a similar displacement of the particle that is located there. The subsequent leftward motion is also transmitted to the next particle, etc. Thus, the oscillations of one air particle are transmitted to the molecule next to it. The second particle is therefore set into oscillation, which in turn initiates oscillation of the next one, and so forth down the line. In other words, each particle vibrates back and forth around its own resting point, and causes successive molecules to vibrate back and forth around their own resting points, as shown schematically in Fig. 1.5. Notice that each molecule vibrates “in place” around its own average position; it is the vibratory pattern that is transmitted through the air. Fig. 1.5 Sound is initiated by transmitting the vibratory pattern of the sound source to nearby air particles, and then the vibratory pattern is passed from particle to particle as a wave. Notice how it is the pattern of vibration that is being transmitted, whereas each particle oscillates around its own average location. This propagation of vibratory motion from particle to particle constitutes the sound wave. This wave appears as alternating compressions and rarefactions radiating from the sound source in all directions, as already suggested in Fig. 1.1. The transmission of particle motion along with the resulting variations in air pressure with distance from the source are represented in Fig. 1.6. Most people are more familiar with the kinds of waves that develop on the surface of a pond when a pebble is dropped into the water. These are transverse waves because the particles are moving at right angles to the direction that the wave is propagating. That is, the water particles oscillate up and down (vertically) even though the wave moves out horizontally from the spot where the pebble hit the water. This principle can be demonstrated by floating a cork in a pool, and then dropping a pebble in the water to start a wave. The floating cork reflects the motions of the water particles. The wave will move out horizontally, but the floating cork bobs up and down (vertically) at right angles to the wave. In contrast, sound waves are longitudinal waves because each air particle oscillates in the same direction in which the wave is propagating (Fig. 1.6). Although sound waves are longitudinal, it is more convenient to draw them with a transverse representation, as in Fig. 1.6. In such a diagram the vertical dimension represents some measure of the size of the signal (e.g., displacement, pressure, etc.), and left to right distance represents time (or distance). For example, the waveform in Fig. 1.6 shows the amount of positive pressure (compression) above the baseline, negative pressure (rarefaction) below the baseline, and distance horizontally going from left to right. Simple harmonic motion is also known as sinusoidal motion, and has a waveform that is called a sinusoidal wave or a sine wave. Let us see why. Fig. 1.7 shows one cycle of a sine wave in the center, surrounded by circles labeled to correspond to points on the wave. Each circle shows a horizontal line corresponding to the horizontal baseline on the sine wave, as well as a radius line (r) that will move around the circle at a fixed speed, much like a clock hand but in a counterclockwise direction. Point a on the waveform in the center of the figure can be viewed as the “starting point” of the cycle. The displacement here is zero because this point is on the horizontal line. The radius appears as shown in circle b when it reaches 45° of rotation, which corresponds to point b on the sine wave. The angle between the radius and the horizontal is called the phase angle (θ) and is a handy way to tell location going around the circle and on the sine wave. In other words, we consider one cycle (one “round trip” of oscillation) to be the same as going around a circle one time. Just as a circle has 360°, we also consider one cycle to have 360°. Since 45/360 = ⅛, a phase angle (θ) of 45° is the same as one eighth of the way around a circle or one eighth of the way into a sine wave. Returning to the circle, the vertical displacement from the horizontal to the point where r intersects the circle is represented by a vertical line labeled d. This vertical line corresponds to the displacement of point b on the sine wave, where the displacement of the air particle is represented by the height of the point above the baseline. Notice that we now have a right triangle in the circle, where r is the hypotenuse, θ is an angle, and d is the leg opposite that angle. Recall from high school math that the sine of an angle equals the length of the opposite leg over the length of the hypotenuse. Here, sin θ = d/r. If we conveniently assume that the length of r is 1, then displacement d becomes the sine of angle θ, which happens to be 0.707. In other words, displacement is determined by the sine of the phase angle, and displacement at any point on the sine wave corresponds to the sine of θ. This is why it is called a sine wave.
 Physical Quantities
Physical Quantities
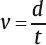
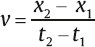
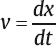

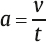
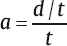
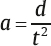
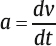
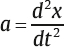
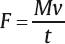

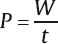

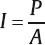

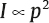

 The Nature of Sound
The Nature of Sound
Simple Harmonic Motion
Sound Waves
The Sinusoidal Function
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree