Fig. 2.1
Schematic of a generic fiber-optic OCT system. Bold lines represent fiber-optic paths, red lines represent free-space optical paths, and thin lines represent electronic signal paths
In the case of TDOCT, the low-coherence source in Fig. 2.1 is broadband and continuous wave (cw), the reference arm delay is repetitively scanned in length, a single-channel (spectrally integrating) photoreceiver is employed, and the required signal processing consists of detecting the envelope of the detected fringe burst pattern corresponding to constructive interference between the reference arm light and each successive scattering site in the sample. FDOCT systems are subdivided into spectral-domain (or spectrometer-based) systems referred to as SDOCT and swept-source systems termed SSOCT (alternatively called OFDI by some authors). In the case of SDOCT, the source is broadband and cw, the reference arm length is fixed at a position approximately corresponding to the position of the sample, and the spectral interference pattern between the light returning from the reference arm and all depths in the sample is dispersed by a spectrometer and collected simultaneously on an array detector such as a charge-coupled device (CCD) or complementary metal-oxide-semiconductor (CMOS) camera. In the case of SSOCT, the source has narrow instantaneous linewidth but is rapidly swept in wavelength, and the spectral interference pattern is detected on a single photoreceiver as a function of time. The reference arm length is also fixed in SSOCT. In both SDOCT and SSOCT forms of FDOCT, the spectral interference pattern encodes in its spectral frequency content the entire depth-resolved structure of the sample at the position of the focal spot, and the A-scan may be recovered as described below using inverse Fourier transformation. Additional signal processing steps may also be required in FDOCT to prepare the spectral interferogram for the inverse Fourier transform, such as interpolation, so that the data is linearly sampled in wave number, addition of phase terms to correct for dispersion mismatches between the sample and reference arms, and others.
2.2 Confocal Gating and Lateral Resolution in OCT Systems
Some previous analyses have described the lateral resolution and axial field of view of OCT systems, as illustrated in Fig. 2.1 as the spot size and depth of focus of an assumed Gaussian profile sample arm beam in the region of the beam focus. This approach is a reasonable approximation and provides useful insight into the trade-off between these quantities specifically that spot size is proportional to the numerical aperture (NA) of the sample arm focusing optics, while the depth of focus is proportional to NA 2. However, it is more correct to treat the sample arm of an OCT system as a reflection-mode scanning confocal microscope, in which the single-mode optical fiber serves as a pinhole aperture for both illumination and collection of light from the sample. Even for OCT systems that do not employ fiber optics, the antenna response function of the homodyne wave mixing inherent to OCT can be shown to be equivalent to confocality [17]. Confocal microscopes using fiberoptic delivery and detection have been well described in the literature, including their lateral and axial point spread function behavior for single- and multimode fiber operation [18–20]. For single-mode optical fibers such as those used in OCT, the expressions for both lateral and axial detected intensities reduce to those for an ideal confocal microscope with a diminishingly small pinhole aperture. Confocal microscopes have the advantage of slightly improved lateral resolution over conventional bright-field microscopes and the ability to perform “optical sectioning” due to their peaked axial response (unlike conventional bright-field microscopes, for which out-of-focus light is blurred, but not attenuated). A summary of results characterizing these quantities in lateral and axial directions is presented in Fig. 2.2. The optical system is assumed to be cylindrically symmetric, so only one lateral dimension is depicted.
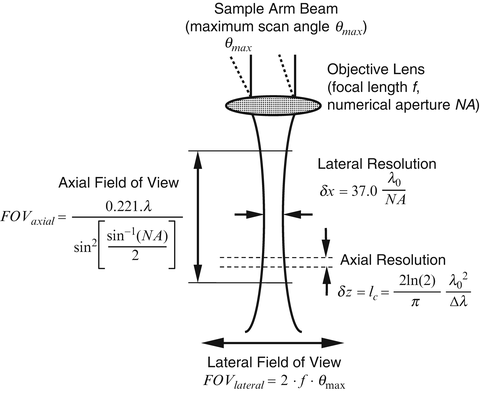

Fig. 2.2
Schematic of generic OCT sample arm optics. Formulas are provided for axial field of view FOV axial and lateral resolution δx (assuming these quantities are dominated by the confocal geometrical optics), axial resolution δz (assuming it is limited by the low-coherence interferometer), and for lateral field of view FOV lateral (assuming a simple f-theta scanning system)
An expression for the detected intensity from a point reflector placed in the focal plane of an ideal reflection confocal microscope as a function of lateral position is given by
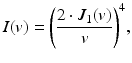
where J 1(v) is a first-order Bessel function of the first kind and v is the normalized lateral range parameter defined by v = 2π ⋅ x ⋅ sin(α)/λ 0. Here, x is the lateral distance from the optical axis, α is half the angular optical aperture subtended by the objective, and λ 0 is the center wavelength of the light source. Note that the numerical aperture of the objective is given by NA = sin(α), assuming that it is properly filled. We interpret Eq. 2.1 as the lateral point spread function of an OCT system at the position of its focal plane and characterize it by defining the lateral resolution δx as its full width at half-maximum (FWHM) power, which calculates to
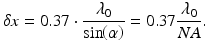
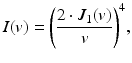
(2.1)
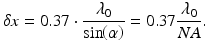
(2.2)
The lateral field of view for an OCT system depends greatly upon the details of the lateral scanning system employed. A particularly simple scanning system employs some means to rotate the sample arm beam through the input aperture of the objective lens to a maximum one-sided scan angle θ max in one or two lateral dimensions. In this case, the lateral field of view of the OCT system is simply given by
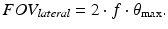
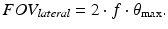
We follow the convention in confocal microscopy [18, 19] and describe the axial response of the OCT sample arm optics as the confocal response to a planar rather than point reflector. The detected intensity of an ideal confocal microscope from a planar reflector as a function of the reflector position along the optic axis is given by
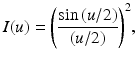
where u is the normalized axial range parameter defined by u = 8π ⋅ z ⋅ sin2(α/2)/λ 0. The axially peaked response of a confocal microscope gives it its well-known depth-sectioning capability. This is also the response we would expect by translating a mirror axially through the focus of an OCT sample arm. If the length of this function is comparable to the axial response of the OCT system arising from low-coherence interferometry (as described below), then the overall axial response of the OCT system should properly be described as the convolution of these two functions. OCT systems operating in this regime have been referred to as optical coherence microscopy or OCM systems [2, 21, 22]. In OCM, however, considerable effort must be expended to align the “confocal” and “coherence” gates and to keep them aligned as depth scanning is performed. In most OCT applications designed for practical clinical and research applications, a relatively low numerical aperture objective is used so that the lateral resolution δx is approximately matched to the axial resolution δz defined by the low-coherence interferometer (see Eq. 2.8), and thus approximately isotropic resolution imaging is performed. Under this condition, the confocal gate length is much larger than the lateral resolution since it scales as the square of the numerical aperture. However, the confocal gate length still limits the axial range over which the low-coherence interferometric depth scanning may usefully operate. We define the FWHM power of the confocal axial response function as the axial field of view FOV axial of the OCT system, which calculates to
![$$ FO{V}_{axial}=\frac{0.221\cdot \lambda }{\mathrm{si}{\mathrm{n}}^2\left[\alpha /2\right]}=\frac{0.221\cdot \lambda }{\mathrm{si}{\mathrm{n}}^2\left[\frac{\mathrm{si}{\mathrm{n}}^{-1}(NA)}{2}\right]}. $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_Equ4.gif)
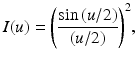
(2.3)
![$$ FO{V}_{axial}=\frac{0.221\cdot \lambda }{\mathrm{si}{\mathrm{n}}^2\left[\alpha /2\right]}=\frac{0.221\cdot \lambda }{\mathrm{si}{\mathrm{n}}^2\left[\frac{\mathrm{si}{\mathrm{n}}^{-1}(NA)}{2}\right]}. $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_Equ4.gif)
(2.4)
2.3 Spatial Coherence Gating in Full-Field OCT Systems
While the preceding discussion has assumed a point-scanning implementation of OCT, the expressions derived for lateral resolution and axial field of view are equally applicable for full-field OCT (FFOCT). FFOCT refers to a class of techniques wherein the entire en face slice of an OCT volume is acquired simultaneously by using a two-dimensional array camera as the detector in a wide-field interferometer. FFOCT has been demonstrated in both time-domain [23, 24] and Fourier-domain [25, 26] implementations. Fourier-domain FFOCT has only been demonstrated using swept sources since a three-dimensional camera would be necessary to obtain the two spatial and one spectral dimensions that would be required for spectrometer-based spectral-domain FFOCT.
An important consideration in the design of FFOCT systems is the management of multiple scattering and crosstalk artifacts [27, 28]. Cross talk originates in scattering samples when multiply scattered light reaches the detector and interferes with singly scattered light originating from the coherence-gated imaging depth in the reference. In point-scanning OCT, the confocal aperture of the single-mode fiber largely rejects multiply scattered light. However, FFOCT systems are implemented in free space and thus lack this confocal aperture. Therefore, multiply scattered photons are detected by the camera, and a subset of these multiply scattered photons will have traveled the correct optical path length to interfere with the reference field.
Cross talk artifacts can be avoided by employing a light source with low spatial coherence [29]. This prevents multiply scattered light in the sample arm from interfering with the reference field, effectively creating a spatial coherence gate that serves the same function as the confocal pinhole in point-scanning OCT. Because of this, thermal sources are often used in FFOCT systems [30, 31]. However, the average number of photons within a coherence volume of blackbody radiation is always on the order of unity [32], which limits the speed and sensitivity of OCT systems employing thermal sources [29, 33, 34]. A strategy to overcome this limit, while still achieving cross talk rejection, is to reduce the spatial coherence of a coherent source, such as a superluminescent diode or femtosecond laser. This can be achieved by piping light of high spatial but low temporal coherence through a multimode fiber that is either dynamically mode mixed [34] or whose length is appropriately selected [35]. In addition, “random” lasers can also produce light with moderate temporal coherence and low spatial coherence and have been used to demonstrate speckle-free laser imaging [36] and cross talk reduction in FFOCT [37].
2.4 Axial Ranging with Low-Coherence Interferometry
The fundamental quality that differentiates optical coherence tomography (OCT) from other forms of optical microscopy is that the predominant axial component of image formation derives from a ranging measurement performed using low-coherence interferometry. Consider the Michelson interferometer illustrated in Fig. 2.3. The interferometer is illuminated by a polychromatic plane wave whose electric field expressed in complex form is E i = s(k, ω)e i(kz−ωt). Here, s(k, ω) is the electric field amplitude as a function of the wave number k = 2π/λ and angular frequency ω = 2πν, which are respectively the spatial and temporal frequencies of each spectral component of the field having wavelength λ. The wavelength λ and frequency ν are coupled by the index of refraction n(λ) (which is wavelength dependent in dispersive media) and vacuum speed of light c according to c/n(λ) = λν. For simplicity of exposition in this section, all distances are assumed to be in free space and thus must be scaled by the appropriate index of refraction to obtain real-space measurements; the detailed effects of sample index and dispersion in OCT are discussed in Sect. 2.7. The beam splitter is assumed to have an achromatic (wavelength-independent) power splitting ratio of 0.5, although a generalization of OCT systems to unequal power splitting [8, 9] or other interferometer topologies (e.g., [8, 38]) is straightforward. The reference reflector is assumed to have electric field reflectivity r R and power reflectivity R R = |r R |2. The reference path is assumed to be in air, and the distance from the beam splitter to the reference reflector is z R .
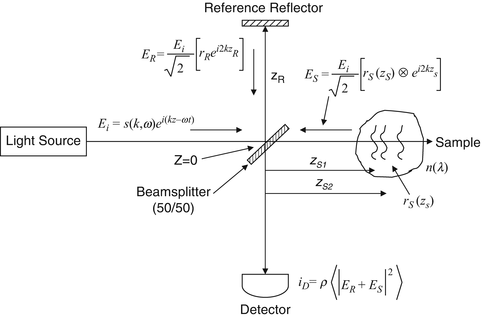

Fig. 2.3
Schematic of a Michelson interferometer used in OCT
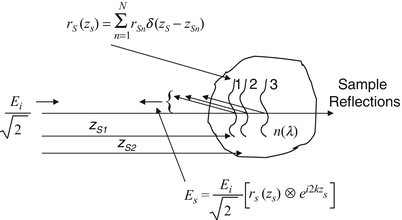
The sample under interrogation is characterized by its depth-dependent electric field reflectivity profile along the sample beam axis r s (z s ), where z s is the path length variable in the sample arm measured from the beam splitter. In general, r s (z s ) is continuous, resulting from the continuously varying refractive index of biological tissues and other samples. It may also be complex, encoding the phase as well as the amplitude of each reflection. However, for an illustrative example, we assume a series of N discrete, real delta-function reflections of the form ![$$ {r}_S\left({z}_s\right)={\displaystyle \sum_{n=1}^N{r}_{Sn}\delta \left[\left({z}_S-{z}_{Sn}\right)\right]} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_IEq1.gif) , with each reflection characterized by its electric field reflectivity r S1, r S2 … and path length from the beam splitter of z S1, z S2 … (see Fig. 2.4). The power reflectivity of each reflector is given by the magnitude squared of the electric field reflectivity, for example, R S1 = ∣r S1∣2. The reconstruction of the function
, with each reflection characterized by its electric field reflectivity r S1, r S2 … and path length from the beam splitter of z S1, z S2 … (see Fig. 2.4). The power reflectivity of each reflector is given by the magnitude squared of the electric field reflectivity, for example, R S1 = ∣r S1∣2. The reconstruction of the function 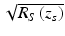 from noninvasive interferometric measurements is the goal of low–coherence interferometry in OCT. The electric field passing through the beam splitter after returning from the sample arm is
from noninvasive interferometric measurements is the goal of low–coherence interferometry in OCT. The electric field passing through the beam splitter after returning from the sample arm is ![$$ {E}_s=\frac{E_i}{\sqrt{2}}\left[{r}_s\left({z}_s\right)\otimes {e}^{i2k{z}_s}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_IEq3.gif) where ⊗ represents convolution and the factor of 2 in the exponential kernel accounts for the round-trip path length to each sample reflection. Note that for most samples such as biological tissues imaged with OCT, sample reflectivities R S1, R S2 … are typically very small (on the order of ∼10−4 to 10−5); thus, the returned reference field typically dominates the reflected sample field. Indeed, selection of the appropriate reference reflectivity is an important criterion in OCT system design [7, 8].
where ⊗ represents convolution and the factor of 2 in the exponential kernel accounts for the round-trip path length to each sample reflection. Note that for most samples such as biological tissues imaged with OCT, sample reflectivities R S1, R S2 … are typically very small (on the order of ∼10−4 to 10−5); thus, the returned reference field typically dominates the reflected sample field. Indeed, selection of the appropriate reference reflectivity is an important criterion in OCT system design [7, 8].
![$$ {r}_S\left({z}_s\right)={\displaystyle \sum_{n=1}^N{r}_{Sn}\delta \left[\left({z}_S-{z}_{Sn}\right)\right]} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_IEq1.gif) , with each reflection characterized by its electric field reflectivity r S1, r S2 … and path length from the beam splitter of z S1, z S2 … (see Fig. 2.4). The power reflectivity of each reflector is given by the magnitude squared of the electric field reflectivity, for example, R S1 = ∣r S1∣2. The reconstruction of the function
, with each reflection characterized by its electric field reflectivity r S1, r S2 … and path length from the beam splitter of z S1, z S2 … (see Fig. 2.4). The power reflectivity of each reflector is given by the magnitude squared of the electric field reflectivity, for example, R S1 = ∣r S1∣2. The reconstruction of the function 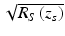 from noninvasive interferometric measurements is the goal of low–coherence interferometry in OCT. The electric field passing through the beam splitter after returning from the sample arm is
from noninvasive interferometric measurements is the goal of low–coherence interferometry in OCT. The electric field passing through the beam splitter after returning from the sample arm is ![$$ {E}_s=\frac{E_i}{\sqrt{2}}\left[{r}_s\left({z}_s\right)\otimes {e}^{i2k{z}_s}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_IEq3.gif) where ⊗ represents convolution and the factor of 2 in the exponential kernel accounts for the round-trip path length to each sample reflection. Note that for most samples such as biological tissues imaged with OCT, sample reflectivities R S1, R S2 … are typically very small (on the order of ∼10−4 to 10−5); thus, the returned reference field typically dominates the reflected sample field. Indeed, selection of the appropriate reference reflectivity is an important criterion in OCT system design [7, 8].
where ⊗ represents convolution and the factor of 2 in the exponential kernel accounts for the round-trip path length to each sample reflection. Note that for most samples such as biological tissues imaged with OCT, sample reflectivities R S1, R S2 … are typically very small (on the order of ∼10−4 to 10−5); thus, the returned reference field typically dominates the reflected sample field. Indeed, selection of the appropriate reference reflectivity is an important criterion in OCT system design [7, 8].
Fig. 2.4
Exemplary model for a sample comprising a series of discrete reflectors
For the example of discrete reflectors, the fields incident on the beam splitter after returning from the reference and sample arms are given by 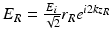 and
and 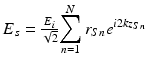 , respectively. The returning fields are halved in power upon passing through the beam splitter again and interfere at the square-law detector, which generates a photocurrent proportional to the square of the sum of the fields incident upon it, given by
, respectively. The returning fields are halved in power upon passing through the beam splitter again and interfere at the square-law detector, which generates a photocurrent proportional to the square of the sum of the fields incident upon it, given by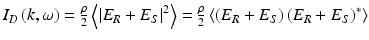 . Here, ρ is the responsivity of the detector (units amperes/watt), the factor of 2 reflects the second pass of each field through the beam splitter, and the angular brackets denote integration over the response time of the detector. Arbitrarily setting z = 0 at the surface of the beam splitter and expanding for the detector current give
. Here, ρ is the responsivity of the detector (units amperes/watt), the factor of 2 reflects the second pass of each field through the beam splitter, and the angular brackets denote integration over the response time of the detector. Arbitrarily setting z = 0 at the surface of the beam splitter and expanding for the detector current give
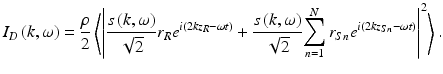
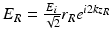 and
and 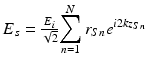 , respectively. The returning fields are halved in power upon passing through the beam splitter again and interfere at the square-law detector, which generates a photocurrent proportional to the square of the sum of the fields incident upon it, given by
, respectively. The returning fields are halved in power upon passing through the beam splitter again and interfere at the square-law detector, which generates a photocurrent proportional to the square of the sum of the fields incident upon it, given by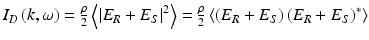 . Here, ρ is the responsivity of the detector (units amperes/watt), the factor of 2 reflects the second pass of each field through the beam splitter, and the angular brackets denote integration over the response time of the detector. Arbitrarily setting z = 0 at the surface of the beam splitter and expanding for the detector current give
. Here, ρ is the responsivity of the detector (units amperes/watt), the factor of 2 reflects the second pass of each field through the beam splitter, and the angular brackets denote integration over the response time of the detector. Arbitrarily setting z = 0 at the surface of the beam splitter and expanding for the detector current give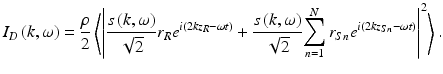
(2.5)
Expanding the magnitude squared functions in Eq. 2.5 eliminates the terms dependent upon the temporal angular frequency ω = 2πν, which is reasonable since ν oscillates much faster than the response time of any detector. This leaves the temporally invariant terms:
![$$ \begin{array}{l}{I}_D(k)=\frac{\rho }{4}\left[S(k)\cdot \left({R}_R+{R}_{S1}+{R}_{S2}+\dots \right)\right]\\ {}\kern3em +\frac{\rho }{4}\left[S(k){\displaystyle \sum_{n=1}^N\sqrt{R_R{R}_{Sn}}\left({e}^{i2k\left({z}_R-{z}_{Sn}\right)}+{e}^{-i2k\left({z}_R-{z}_{Sn}\right)}\right)}\right]\\ {}\kern3em +\frac{\rho }{4}\left[S(k){\displaystyle \sum_{n\ne m=1}^N\sqrt{R_{Sn}{R}_{Sm}}\left({e}^{i2k\left({z}_{Sn}-{z}_{Sm}\right)}+{e}^{-i2k\left({z}_{Sn}-{z}_{Sm}\right)}\right)}\right].\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_Equ6.gif)
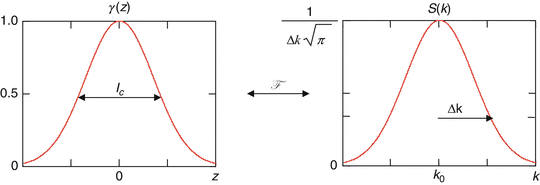
Here, S(k) = 〈|s(k, ω|2〉 is substituted, which encodes the power spectral dependence of the light source. As an illustrative example, a Gaussian-shaped light source spectrum is convenient to use in modeling OCT because it approximates the shape of actual light sources and also has useful Fourier transform properties. The normalized Gaussian function S(k) and its inverse Fourier transform γ(z) are given by
![$$ \gamma (z)={e}^{-{(z)}^2\Delta {k}^2}\overset{F}{\leftrightarrow }S(k)=\frac{1}{\Delta k\sqrt{\pi }}{e}^{-{\left[\frac{\left(k-{k}_0\right)}{\Delta k}\right]}^2} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_Equ7.gif)
and are illustrated in Fig. 2.5. Here, k 0 represents the central wave number of the light source spectrum, and Δk represents its spectral bandwidth, corresponding to the half-width of the spectrum at 1/e of its maximum. As will be seen below, the inverse Fourier transform γ(z), hereafter called the “coherence function,” dominates the axial point spread function (PSF) in OCT imaging systems (in OCT systems employing a low numerical aperture focusing objective, as pointed out in Sect. 2.2). The PSF is commonly characterized by its full width at half the maximum (FWHM) value and is the definition of the round-trip “coherence length” of the light source l c . The free-space coherence length is an explicit function of the light source bandwidth, stated in both wave number and wavelength terms as
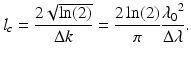
![$$ \begin{array}{l}{I}_D(k)=\frac{\rho }{4}\left[S(k)\cdot \left({R}_R+{R}_{S1}+{R}_{S2}+\dots \right)\right]\\ {}\kern3em +\frac{\rho }{4}\left[S(k){\displaystyle \sum_{n=1}^N\sqrt{R_R{R}_{Sn}}\left({e}^{i2k\left({z}_R-{z}_{Sn}\right)}+{e}^{-i2k\left({z}_R-{z}_{Sn}\right)}\right)}\right]\\ {}\kern3em +\frac{\rho }{4}\left[S(k){\displaystyle \sum_{n\ne m=1}^N\sqrt{R_{Sn}{R}_{Sm}}\left({e}^{i2k\left({z}_{Sn}-{z}_{Sm}\right)}+{e}^{-i2k\left({z}_{Sn}-{z}_{Sm}\right)}\right)}\right].\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_Equ6.gif)
(2.6)
![$$ \gamma (z)={e}^{-{(z)}^2\Delta {k}^2}\overset{F}{\leftrightarrow }S(k)=\frac{1}{\Delta k\sqrt{\pi }}{e}^{-{\left[\frac{\left(k-{k}_0\right)}{\Delta k}\right]}^2} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_Equ7.gif)
(2.7)

Fig. 2.5
Illustration of Fourier transform relationship between the Gaussian-shaped coherence function γ(z) (characterized by the coherence length l c ) and the light source spectrum S(k) (characterized by the central wave number k 0 and wave number bandwidth Δk)
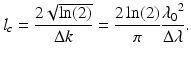
(2.8)
Here, 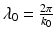 is the center wavelength of the light source, and Δλ is its wavelength bandwidth, defined as the FWHM of its wavelength spectrum
is the center wavelength of the light source, and Δλ is its wavelength bandwidth, defined as the FWHM of its wavelength spectrum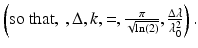 Note the inverse relationship between the coherence length and the light source bandwidth.
Note the inverse relationship between the coherence length and the light source bandwidth.
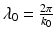 is the center wavelength of the light source, and Δλ is its wavelength bandwidth, defined as the FWHM of its wavelength spectrum
is the center wavelength of the light source, and Δλ is its wavelength bandwidth, defined as the FWHM of its wavelength spectrum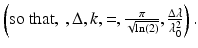 Note the inverse relationship between the coherence length and the light source bandwidth.
Note the inverse relationship between the coherence length and the light source bandwidth.Using Euler’s rule to simplify Eq. 2.6 generates a real result for the detector current as a function of wave number, commonly known as the “spectral interferogram”:
![$$ \begin{array}{l}{I}_D(k)=\frac{\rho }{4}\left[S(k)\left[{R}_R+{R}_{S1}+{R}_{S2}+\dots \right]\right]\kern1.5em ``\mathrm{D}\mathrm{C}\ \mathrm{Terms}"\\ {}+\frac{\rho }{2}\left[S(k){\displaystyle \sum_{n=1}^N\sqrt{R_R{R}_{Sn}}\left( \cos \left[2k\left({z}_R-{z}_{Sn}\right)\right]\right)}\right]\kern1.5em ``\mathrm{Cross}\hbox{-} \mathrm{correlation}\ \mathrm{Terms}"\\ {}+\frac{\rho }{4}\left[S(k){\displaystyle \sum_{n\ne m=1}^N\sqrt{R_{Sn}{R}_{Sm}} \cos \left[2k\left({z}_{Sn}-{z}_{Sm}\right.\right]}\right]\kern1.5em ``\mathrm{Auto}\hbox{-} \mathrm{correlation}\ \mathrm{Terms}"\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_Equ9.gif)
![$$ \begin{array}{l}{I}_D(k)=\frac{\rho }{4}\left[S(k)\left[{R}_R+{R}_{S1}+{R}_{S2}+\dots \right]\right]\kern1.5em ``\mathrm{D}\mathrm{C}\ \mathrm{Terms}"\\ {}+\frac{\rho }{2}\left[S(k){\displaystyle \sum_{n=1}^N\sqrt{R_R{R}_{Sn}}\left( \cos \left[2k\left({z}_R-{z}_{Sn}\right)\right]\right)}\right]\kern1.5em ``\mathrm{Cross}\hbox{-} \mathrm{correlation}\ \mathrm{Terms}"\\ {}+\frac{\rho }{4}\left[S(k){\displaystyle \sum_{n\ne m=1}^N\sqrt{R_{Sn}{R}_{Sm}} \cos \left[2k\left({z}_{Sn}-{z}_{Sm}\right.\right]}\right]\kern1.5em ``\mathrm{Auto}\hbox{-} \mathrm{correlation}\ \mathrm{Terms}"\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_Equ9.gif)
(2.9)
The result in Eq. 2.6 includes three distinct components:
1.
A path length-independent offset to the detector current, scaled by the light source wave number spectrum and with amplitude proportional to the power reflectivity of the reference mirror plus the sum of the sample reflectivities. This term is often referred to as “constant” or “DC” component. This is the largest component of the detector current if the reference reflectivity dominates the sample reflectivity.
2.
A “cross-correlation” component for each sample reflector, which depends upon both the light source wave number and the path length difference between the reference arm and sample reflectors. This is the desired component for OCT imaging. Since these components are proportional to the square root of the sample reflectivities, they are typically smaller than the DC component. However, the square root dependence represents an important logarithmic gain factor over the direct detection of sample reflections.
3.
“Autocorrelation” terms representing interference occurring between the different sample reflectors appear as artifacts in typical OCT system designs (exceptions occur in common-path system designs, in which the autocorrelation component represents the desired signal). Since the autocorrelation terms depend linearly upon the power reflectivity of the sample reflections, a primary tool for decreasing autocorrelation artifacts is the selection of the proper reference reflectivity so that the autocorrelation terms are small compared to the DC and interferometric terms.
It is useful to gain an intuitive understanding of the form of Eq. 2.9, as well as the effect that different source spectra and different numbers of sample reflectors and their distributions have upon it. For a single reflector, only DC and a single interferometric term are present, and the source spectrum is modulated by a simple cosinusoid whose period is proportional to the distance between the sample and reference reflectors, as illustrated in Fig. 2.6. In addition, the amplitude of spectral modulation or “visibility” of the spectral fringes is proportional to the amplitude reflectivity of the sample reflector 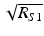 . For the case of multiple reflectors, the spectrum is modulated by multiple cosinusoids, each having a frequency and amplitude characteristic of the sample reflection that gives rise to it. In addition, if more than one reflector is present in the sample, autocorrelation components modulated according to the path length difference between the sample reflectors and proportional to the product of their amplitude reflectivities also appear. Since the sample amplitude reflectivities are usually small compared to the reference reflection, the autocorrelation terms are usually small compared to the cross-correlation terms. Also, since reflections in the sample tend to be clumped closely together compared to the distance between the sample and the reference reflector, the autocorrelation term modulation frequencies also tend to be small.
. For the case of multiple reflectors, the spectrum is modulated by multiple cosinusoids, each having a frequency and amplitude characteristic of the sample reflection that gives rise to it. In addition, if more than one reflector is present in the sample, autocorrelation components modulated according to the path length difference between the sample reflectors and proportional to the product of their amplitude reflectivities also appear. Since the sample amplitude reflectivities are usually small compared to the reference reflection, the autocorrelation terms are usually small compared to the cross-correlation terms. Also, since reflections in the sample tend to be clumped closely together compared to the distance between the sample and the reference reflector, the autocorrelation term modulation frequencies also tend to be small.
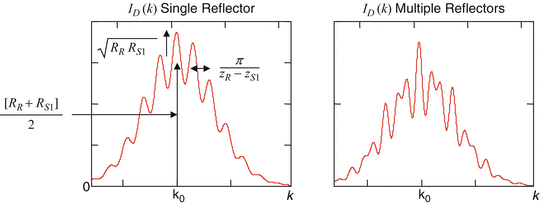
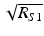 . For the case of multiple reflectors, the spectrum is modulated by multiple cosinusoids, each having a frequency and amplitude characteristic of the sample reflection that gives rise to it. In addition, if more than one reflector is present in the sample, autocorrelation components modulated according to the path length difference between the sample reflectors and proportional to the product of their amplitude reflectivities also appear. Since the sample amplitude reflectivities are usually small compared to the reference reflection, the autocorrelation terms are usually small compared to the cross-correlation terms. Also, since reflections in the sample tend to be clumped closely together compared to the distance between the sample and the reference reflector, the autocorrelation term modulation frequencies also tend to be small.
. For the case of multiple reflectors, the spectrum is modulated by multiple cosinusoids, each having a frequency and amplitude characteristic of the sample reflection that gives rise to it. In addition, if more than one reflector is present in the sample, autocorrelation components modulated according to the path length difference between the sample reflectors and proportional to the product of their amplitude reflectivities also appear. Since the sample amplitude reflectivities are usually small compared to the reference reflection, the autocorrelation terms are usually small compared to the cross-correlation terms. Also, since reflections in the sample tend to be clumped closely together compared to the distance between the sample and the reference reflector, the autocorrelation term modulation frequencies also tend to be small.
Fig. 2.6
Important features of the spectral interferogram. For a single sample reflector of field reflectivity r S1 = 0.1 (left), the cross-correlation component with amplitude 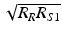 and wave number period
and wave number period 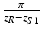 rides on top of the DC term of amplitude
rides on top of the DC term of amplitude ![$$ \frac{\left[{R}_R+{R}_{S1}\right]}{2} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_IEq12.gif) (factors of ρS(k) are left out for clarity). For multiple reflectors, the cross-correlation component is a superposition of cosinusoids
(factors of ρS(k) are left out for clarity). For multiple reflectors, the cross-correlation component is a superposition of cosinusoids
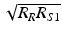 and wave number period
and wave number period 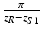 rides on top of the DC term of amplitude
rides on top of the DC term of amplitude ![$$ \frac{\left[{R}_R+{R}_{S1}\right]}{2} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_IEq12.gif) (factors of ρS(k) are left out for clarity). For multiple reflectors, the cross-correlation component is a superposition of cosinusoids
(factors of ρS(k) are left out for clarity). For multiple reflectors, the cross-correlation component is a superposition of cosinusoids2.5 Fourier-Domain Low-Coherence Interferometry
In Fourier-domain OCT (FDOCT), the wave number-dependent detector current I D (k) in Eq. 2.9 is captured and processed using Fourier analysis to reconstruct an approximation of the internal sample reflectivity profile 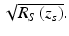 The process for capturing I D (k) depends upon the experimental details of the detection apparatus. In spectral-domain OCT (SDOCT, also called spectrometer-based OCT), a broadband light source is used, and all spectral components of I D (k) are captured simultaneously on a detector array placed at the output of a spectrometer [39–41]. In swept-source OCT (SSOCT, also called optical frequency-domain imaging or OFDI), the spectral components of I D (k) are captured sequentially by recording the signal in a single detector while synchronously sweeping the wave number of a narrowband swept-laser source [42–45].
The process for capturing I D (k) depends upon the experimental details of the detection apparatus. In spectral-domain OCT (SDOCT, also called spectrometer-based OCT), a broadband light source is used, and all spectral components of I D (k) are captured simultaneously on a detector array placed at the output of a spectrometer [39–41]. In swept-source OCT (SSOCT, also called optical frequency-domain imaging or OFDI), the spectral components of I D (k) are captured sequentially by recording the signal in a single detector while synchronously sweeping the wave number of a narrowband swept-laser source [42–45].
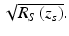 The process for capturing I D (k) depends upon the experimental details of the detection apparatus. In spectral-domain OCT (SDOCT, also called spectrometer-based OCT), a broadband light source is used, and all spectral components of I D (k) are captured simultaneously on a detector array placed at the output of a spectrometer [39–41]. In swept-source OCT (SSOCT, also called optical frequency-domain imaging or OFDI), the spectral components of I D (k) are captured sequentially by recording the signal in a single detector while synchronously sweeping the wave number of a narrowband swept-laser source [42–45].
The process for capturing I D (k) depends upon the experimental details of the detection apparatus. In spectral-domain OCT (SDOCT, also called spectrometer-based OCT), a broadband light source is used, and all spectral components of I D (k) are captured simultaneously on a detector array placed at the output of a spectrometer [39–41]. In swept-source OCT (SSOCT, also called optical frequency-domain imaging or OFDI), the spectral components of I D (k) are captured sequentially by recording the signal in a single detector while synchronously sweeping the wave number of a narrowband swept-laser source [42–45].The sample reflectivity profile r s (z s ) is estimated from the inverse Fourier transform of I D (k). Making use of the Fourier transform pair ![$$ \frac{1}{2}\left(\delta \left[\left(z+{z}_0\right)\right]+\delta \left[\left(z-{z}_0\right)\right]\right)\overset{F}{\leftrightarrow } \cos k{z}_0 $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_IEq14.gif) and the convolution property of Fourier transforms
and the convolution property of Fourier transforms 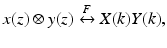 the inverse Fourier transform of Eq. 2.9 may be calculated as
the inverse Fourier transform of Eq. 2.9 may be calculated as
![$$ \begin{array}{l}{i}_D(z)=\kern0.4em \frac{\rho }{8}\left[\gamma (z)\left[{R}_R+{R}_{S1}+{R}_{S2}+\dots \right]\right]\kern0.2em ``\mathrm{D}\mathrm{C}\ \mathrm{terms}"\\ {}\kern5.4em +\frac{\rho }{4}\left[\gamma (z)\otimes {\displaystyle \sum_{n=1}^N\sqrt{R_R{R}_{Sn}}\left(\delta \left[\left(z\pm 2\left({z}_R-{z}_{Sn}\right)\right)\right]\right)}\right]\ ``\mathrm{Cross}\hbox{-} \mathrm{correlation}\kern0.5em \mathrm{terms}"\\ {}\kern5.4em +\frac{\rho }{8}\left[\gamma (z)\otimes {\displaystyle \sum_{n\ne m=1}^N\sqrt{R_{Sn}{R}_{Sm}}\left(\delta \left[\left(z\pm 2\left({z}_{Sn}-{z}_{Sm}\right)\right)\right]\right)}\right]\ ``\mathrm{Auto}\hbox{-} \mathrm{correlation}\kern0.5em \mathrm{terms}."\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_Equ10.gif)
![$$ \frac{1}{2}\left(\delta \left[\left(z+{z}_0\right)\right]+\delta \left[\left(z-{z}_0\right)\right]\right)\overset{F}{\leftrightarrow } \cos k{z}_0 $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_IEq14.gif) and the convolution property of Fourier transforms
and the convolution property of Fourier transforms 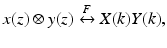 the inverse Fourier transform of Eq. 2.9 may be calculated as
the inverse Fourier transform of Eq. 2.9 may be calculated as![$$ \begin{array}{l}{i}_D(z)=\kern0.4em \frac{\rho }{8}\left[\gamma (z)\left[{R}_R+{R}_{S1}+{R}_{S2}+\dots \right]\right]\kern0.2em ``\mathrm{D}\mathrm{C}\ \mathrm{terms}"\\ {}\kern5.4em +\frac{\rho }{4}\left[\gamma (z)\otimes {\displaystyle \sum_{n=1}^N\sqrt{R_R{R}_{Sn}}\left(\delta \left[\left(z\pm 2\left({z}_R-{z}_{Sn}\right)\right)\right]\right)}\right]\ ``\mathrm{Cross}\hbox{-} \mathrm{correlation}\kern0.5em \mathrm{terms}"\\ {}\kern5.4em +\frac{\rho }{8}\left[\gamma (z)\otimes {\displaystyle \sum_{n\ne m=1}^N\sqrt{R_{Sn}{R}_{Sm}}\left(\delta \left[\left(z\pm 2\left({z}_{Sn}-{z}_{Sm}\right)\right)\right]\right)}\right]\ ``\mathrm{Auto}\hbox{-} \mathrm{correlation}\kern0.5em \mathrm{terms}."\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_Equ10.gif)
(2.10)
Note that the desired sample field reflectivity profile ![$$ \sqrt{R_S\left({z}_s\right)}={\displaystyle \sum_{n=1}^N\sqrt{R_{Sn}}\delta \left[\left({z}_S-{z}_{Sn}\right)\right]} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_IEq16.gif) is indeed embedded within the cross-correlation terms of Eq. 2.10, although it is surrounded by several confounding factors. Carrying out the convolutions by taking advantage of the sifting property of the delta function, we obtain the result of the interferometric measurement, referred to as the “A-scan”:
is indeed embedded within the cross-correlation terms of Eq. 2.10, although it is surrounded by several confounding factors. Carrying out the convolutions by taking advantage of the sifting property of the delta function, we obtain the result of the interferometric measurement, referred to as the “A-scan”:
![$$ \begin{array}{l}{i}_D(z)=\frac{\rho }{8}\left[\gamma (z)\left[{R}_R+{R}_{S1}+{R}_{S2}+\dots \right]\right]\\ {}\kern1em +\frac{\rho }{4}{\displaystyle \sum_{n=1}^N\sqrt{R_R{R}_{Sn}}\left[\gamma \left[2\left({z}_R-{z}_{Sn}\right)\right]+\gamma \left[-2\left({z}_R-{z}_{Sn}\right)\right]\right]}\\ {}\kern1em +\frac{\rho }{8}{\displaystyle \sum_{n\ne m=1}^N\sqrt{R_{Sn}{R}_{Sm}}\left[\gamma \left[2\left({z}_{Sn}-{z}_{Sm}\right)\right]+\gamma \left[-2\left({z}_{Sn}-{z}_{Sm}\right)\right]\right]}.\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_Equ11.gif)
![$$ \sqrt{R_S\left({z}_s\right)}={\displaystyle \sum_{n=1}^N\sqrt{R_{Sn}}\delta \left[\left({z}_S-{z}_{Sn}\right)\right]} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_IEq16.gif) is indeed embedded within the cross-correlation terms of Eq. 2.10, although it is surrounded by several confounding factors. Carrying out the convolutions by taking advantage of the sifting property of the delta function, we obtain the result of the interferometric measurement, referred to as the “A-scan”:
is indeed embedded within the cross-correlation terms of Eq. 2.10, although it is surrounded by several confounding factors. Carrying out the convolutions by taking advantage of the sifting property of the delta function, we obtain the result of the interferometric measurement, referred to as the “A-scan”:![$$ \begin{array}{l}{i}_D(z)=\frac{\rho }{8}\left[\gamma (z)\left[{R}_R+{R}_{S1}+{R}_{S2}+\dots \right]\right]\\ {}\kern1em +\frac{\rho }{4}{\displaystyle \sum_{n=1}^N\sqrt{R_R{R}_{Sn}}\left[\gamma \left[2\left({z}_R-{z}_{Sn}\right)\right]+\gamma \left[-2\left({z}_R-{z}_{Sn}\right)\right]\right]}\\ {}\kern1em +\frac{\rho }{8}{\displaystyle \sum_{n\ne m=1}^N\sqrt{R_{Sn}{R}_{Sm}}\left[\gamma \left[2\left({z}_{Sn}-{z}_{Sm}\right)\right]+\gamma \left[-2\left({z}_{Sn}-{z}_{Sm}\right)\right]\right]}.\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_Equ11.gif)
(2.11)
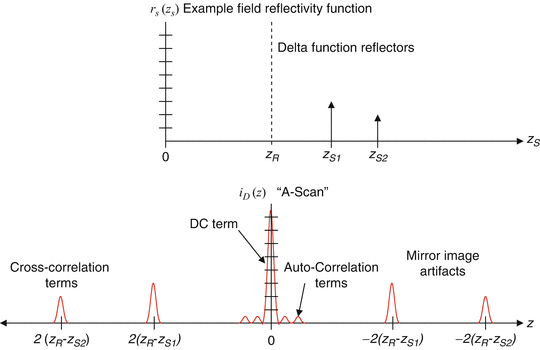
The results in Eqs. 2.10 and 2.11 for the example of discrete sample reflectors and a Gaussian-shaped source spectrum are plotted in Fig. 2.7. As can be seen in the figure, the sample field reflectivity profile ![$$ \sqrt{R_S\left({z}_s\right)}={\displaystyle \sum_{n=1}^N\sqrt{R_{Sn}}\delta \left[\left({z}_S-{z}_{Sn}\right)\right]} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_IEq17.gif) is reproduced in the cross-correlation terms, with the following modifications: First, the sample reflectivity profile appears as a function of the reference coordinate z R , rather than the sample coordinate z S . Second, the apparent displacement of each sample reflector from the reference position is doubled (which can be understood from the fact that the interferometer measures the round-trip distance to each reflector). We accommodate this by defining a new single-pass depth variable
is reproduced in the cross-correlation terms, with the following modifications: First, the sample reflectivity profile appears as a function of the reference coordinate z R , rather than the sample coordinate z S . Second, the apparent displacement of each sample reflector from the reference position is doubled (which can be understood from the fact that the interferometer measures the round-trip distance to each reflector). We accommodate this by defining a new single-pass depth variable 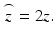 Third, each reflector appears broadened or blurred out to a width of about a coherence length by convolution with the function γ(z). This is precisely the definition of an imaging system PSF. Given the inverse relationship of the coherence length to the light source bandwidth, the clearest path to increasing the fidelity of the estimate of
Third, each reflector appears broadened or blurred out to a width of about a coherence length by convolution with the function γ(z). This is precisely the definition of an imaging system PSF. Given the inverse relationship of the coherence length to the light source bandwidth, the clearest path to increasing the fidelity of the estimate of 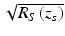 is to use as broad-bandwidth sources as possible. Fourth, the magnitude of the detected sample reflectivity, which can be very small, is amplified by the large homodyne gain factor represented by the strong reference reflectivity
is to use as broad-bandwidth sources as possible. Fourth, the magnitude of the detected sample reflectivity, which can be very small, is amplified by the large homodyne gain factor represented by the strong reference reflectivity 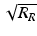 . All of the modifications listed so far can be dealt with through proper interpretation of the data, that is, the realization that the zero position corresponds to the position of the reference reflector, relabeling axial distances to account for the factor of 2, and accounting for the homodyne gain factor.
. All of the modifications listed so far can be dealt with through proper interpretation of the data, that is, the realization that the zero position corresponds to the position of the reference reflector, relabeling axial distances to account for the factor of 2, and accounting for the homodyne gain factor.
![$$ \sqrt{R_S\left({z}_s\right)}={\displaystyle \sum_{n=1}^N\sqrt{R_{Sn}}\delta \left[\left({z}_S-{z}_{Sn}\right)\right]} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_IEq17.gif) is reproduced in the cross-correlation terms, with the following modifications: First, the sample reflectivity profile appears as a function of the reference coordinate z R , rather than the sample coordinate z S . Second, the apparent displacement of each sample reflector from the reference position is doubled (which can be understood from the fact that the interferometer measures the round-trip distance to each reflector). We accommodate this by defining a new single-pass depth variable
is reproduced in the cross-correlation terms, with the following modifications: First, the sample reflectivity profile appears as a function of the reference coordinate z R , rather than the sample coordinate z S . Second, the apparent displacement of each sample reflector from the reference position is doubled (which can be understood from the fact that the interferometer measures the round-trip distance to each reflector). We accommodate this by defining a new single-pass depth variable 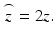 Third, each reflector appears broadened or blurred out to a width of about a coherence length by convolution with the function γ(z). This is precisely the definition of an imaging system PSF. Given the inverse relationship of the coherence length to the light source bandwidth, the clearest path to increasing the fidelity of the estimate of
Third, each reflector appears broadened or blurred out to a width of about a coherence length by convolution with the function γ(z). This is precisely the definition of an imaging system PSF. Given the inverse relationship of the coherence length to the light source bandwidth, the clearest path to increasing the fidelity of the estimate of 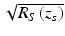 is to use as broad-bandwidth sources as possible. Fourth, the magnitude of the detected sample reflectivity, which can be very small, is amplified by the large homodyne gain factor represented by the strong reference reflectivity
is to use as broad-bandwidth sources as possible. Fourth, the magnitude of the detected sample reflectivity, which can be very small, is amplified by the large homodyne gain factor represented by the strong reference reflectivity 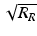 . All of the modifications listed so far can be dealt with through proper interpretation of the data, that is, the realization that the zero position corresponds to the position of the reference reflector, relabeling axial distances to account for the factor of 2, and accounting for the homodyne gain factor.
. All of the modifications listed so far can be dealt with through proper interpretation of the data, that is, the realization that the zero position corresponds to the position of the reference reflector, relabeling axial distances to account for the factor of 2, and accounting for the homodyne gain factor.
Fig. 2.7
Illustration of the example discrete-reflector sample field reflectivity function 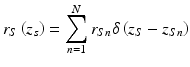 (top) and the A-scan resulting from Fourier-domain low-coherence interferometry
(top) and the A-scan resulting from Fourier-domain low-coherence interferometry
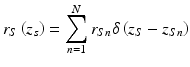 (top) and the A-scan resulting from Fourier-domain low-coherence interferometry
(top) and the A-scan resulting from Fourier-domain low-coherence interferometryA number of additional modifications to the field reflectivity profile are termed artifacts and are more serious. First, as seen in the cross-correlation terms in Eqs. 2.10 and 2.11, a mirror image of the blurred version of 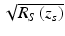 appears on the opposite side of zero path length, that is, the reference reflector position. This is termed the complex conjugate artifact in FDOCT and is simply understood from the fact that since the detected interferometric spectrum is necessarily real, its inverse Fourier transform must be Hermitian symmetric, that is, its values at positive and negative distances are complex conjugates of each other, and therefore if they are real, they must be identical. This artifact is not disabling so long as the sample can be kept entirely to one side of zero path length, in which case it can be dealt with by simply only displaying the positive or negative distances. However, if the sample strays over the zero path length border, it begins to overlap its mirror image, an effect that cannot be removed by image processing alone. A number of approaches have been described for removing this complex conjugate artifact ([46–53]; also see Sect. 2.8.2).
appears on the opposite side of zero path length, that is, the reference reflector position. This is termed the complex conjugate artifact in FDOCT and is simply understood from the fact that since the detected interferometric spectrum is necessarily real, its inverse Fourier transform must be Hermitian symmetric, that is, its values at positive and negative distances are complex conjugates of each other, and therefore if they are real, they must be identical. This artifact is not disabling so long as the sample can be kept entirely to one side of zero path length, in which case it can be dealt with by simply only displaying the positive or negative distances. However, if the sample strays over the zero path length border, it begins to overlap its mirror image, an effect that cannot be removed by image processing alone. A number of approaches have been described for removing this complex conjugate artifact ([46–53]; also see Sect. 2.8.2).
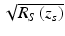 appears on the opposite side of zero path length, that is, the reference reflector position. This is termed the complex conjugate artifact in FDOCT and is simply understood from the fact that since the detected interferometric spectrum is necessarily real, its inverse Fourier transform must be Hermitian symmetric, that is, its values at positive and negative distances are complex conjugates of each other, and therefore if they are real, they must be identical. This artifact is not disabling so long as the sample can be kept entirely to one side of zero path length, in which case it can be dealt with by simply only displaying the positive or negative distances. However, if the sample strays over the zero path length border, it begins to overlap its mirror image, an effect that cannot be removed by image processing alone. A number of approaches have been described for removing this complex conjugate artifact ([46–53]; also see Sect. 2.8.2).
appears on the opposite side of zero path length, that is, the reference reflector position. This is termed the complex conjugate artifact in FDOCT and is simply understood from the fact that since the detected interferometric spectrum is necessarily real, its inverse Fourier transform must be Hermitian symmetric, that is, its values at positive and negative distances are complex conjugates of each other, and therefore if they are real, they must be identical. This artifact is not disabling so long as the sample can be kept entirely to one side of zero path length, in which case it can be dealt with by simply only displaying the positive or negative distances. However, if the sample strays over the zero path length border, it begins to overlap its mirror image, an effect that cannot be removed by image processing alone. A number of approaches have been described for removing this complex conjugate artifact ([46–53]; also see Sect. 2.8.2).Additional image artifacts also arise from the DC and autocorrelation terms in Eqs. 2.10 and 2.11. The DC terms give rise to a large artifactual signal centered at zero path length difference. The FWHM value of the DC artifact is only one coherence length wide; however, the signal amplitude is so much larger than the desired cross-correlation terms that the wings of the Gaussian-shaped PSF from Eq. 2.7 can overwhelm the desired signal components much farther away. Since the largest component of the DC artifact comes from the reference reflector (with reflectivity near 1), a simple method to eliminate that component is to record the amplitude of the spectral interferometric signal Eq. 2.9 with the reference reflector but no sample present and then to subtract this signal component from each subsequent spectral interferometric signal acquired. The autocorrelation terms in Eqs. 2.10 and 2.11 also give rise to artificial signals at and near the zero path length position, since the distance between reflectors in a sample is typically much smaller than the distance between the sample reflectors and the reference arm path length. The best method to eliminate the autocorrelation signals is to ensure that the reference reflectivity is sufficient so that the amplitude of the autocorrelation terms is very small compared to the cross-correlation terms.
2.6 Time-Domain Low-Coherence Interferometry
In traditional or time-domain OCT (TDOCT), the wave number-dependent detector current I D (k) in Eq. 2.9 is captured on a single receiver, while the reference delay z r is scanned to reconstruct an approximation of the internal sample reflectivity profile 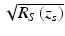 . The result is obtained by the integration of Eq. 2.9 over all k:
. The result is obtained by the integration of Eq. 2.9 over all k:
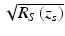 . The result is obtained by the integration of Eq. 2.9 over all k:
. The result is obtained by the integration of Eq. 2.9 over all k:
![$$ \begin{array}{l}{I}_D\left({z}_R\right)=\frac{\rho }{4}\left[{S}_0\left[{R}_R+{R}_{S1}+{R}_{S2}+\dots \right]\right]\kern1em ``\mathrm{D}\mathrm{C}\kern0.5em \mathrm{offset}"\\ {}\kern4em +\frac{\rho }{2}\left[{S}_0{\displaystyle \sum_{n=1}^N\sqrt{R_R{R}_{Sn}}{e}^{-{\left[\left({z}_R-{z}_{Sn}\right)\right]}^2\Delta {k}^2}\kern0.2em \cos \left[2{k}_0\left({z}_R-{z}_{Sn}\right)\right]}\right]\kern1em ``\mathrm{Fringe}\kern0.5em \mathrm{bursts}."\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_3_Chapter_Equ12.gif)


