(33.1)
where E = A + i B represents a vector of complex amplitude that lies in the xy-plane. In a particular plane, say z = 0 for convenience, the tip of the electric field traces out a curve known as the vibrational ellipse, given by
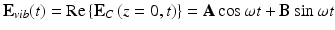
(33.2)
If the real vector A = 0 (or B = 0), the vibrational ellipse collapses to a straight line and the wave is said to be linearly polarized along the direction of B (or A). If |A| = |B| and A · B = 0, the vibrational ellipse is a circle and the wave is said to be circularly polarized. In general, a monochromatic wave of the form in Eq. 33.2 is elliptically polarized (Fig. 33.1).
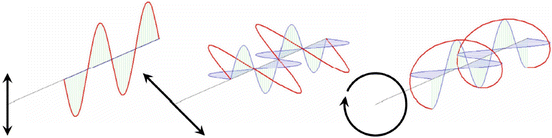

Fig. 33.1
Vibrational ellipses (from left to right) for vertically linear polarized light, linear polarized light oriented at 45° with respect to the vertical and horizontal orientations, and circularly polarized light
The effect of light propagation through a material with a complex index of refraction, N = n + iκ, can be seen through expansion of Eq. 33.1 to yield
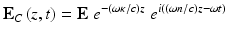
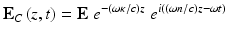
(33.3)
It can be inferred that the imaginary part of the complex refractive index, κ, determines the attenuation of the wave as it propagates through the medium and that the real part, n, determines the phase velocity. There are a wide variety of media in which the index of refraction is independent of the polarization state of light. In these cases, light can propagate with no change of its polarization state. However, there are also many materials for which this is not the case. The goal of PS-OCT is to ascertain these light-polarization changing properties of a sample.
A material is said to be birefringent if the real part of its refractive index is polarization state dependent. Calcite is a classic example of a crystal with uniaxial birefringence; the difference in the real part of the refractive index of calcite causes light traveling through it to decompose into two beams that travel at different speeds. The orientation of this decomposition depends on that of the crystal and will be along and orthogonal to the material optic axis. Assuming a difference in refractive index of Δn, the two beams will experience a phase retardation, η, given by
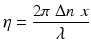
where x is the distance traveled through the birefringent material. This phase retardation leads to an alteration of the resultant polarization state of the wave. Organized linear structures can exhibit form birefringence. This includes a variety of biological tissues, such as tendon, muscle, nerve, bone, cartilage, and teeth.
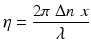
(33.4)
A difference in the imaginary portion of the refractive index leads to a differential attenuation of polarization states. Materials exhibiting this quality are termed dichroic. The differential attenuation experienced by light traveling through a dichroic material can be quantified by an amount of diattenuation, d, given by the ratio [26, 27]
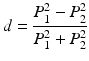
where P 1 and P 2 are the electric field amplitude attenuation ratios for light polarized along and orthogonal to the optic axis of the material. These amplitude attenuation ratios, P i , can be derived directly from the corresponding imaginary portion of refractive index, κ i , according to the relation
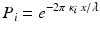
where x is the distance traveled through the dichroic material. It should be noted that, unlike phase retardation, neither the amplitude attenuation ratios nor diattenuation scale linearly with the distance traveled through the tissue. While similar measures such as biattenuance [28, 29], defined simply as the difference in the imaginary portions of the refractive index of a dichroic material, have been recently introduced, diattenuation remains the more commonly used measure of differential attenuation.
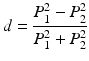
(33.5)
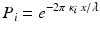
(33.6)
33.1.1 Jones Formalism I
The Jones formalism provides a convenient mathematical description of polarized light and polarization effects [30]. In this section, an introduction to this calculus will be followed by its application to a simplified analysis of early PS-OCT systems.
33.1.1.1 Jones Vectors
In the previous discussion of vibrational ellipses, the complex vector E was described in terms of its real and imaginary parts, A and B. A somewhat more useful decomposition can be done in terms of a pair of orthonormal basis vectors to yield
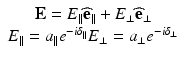
where  and
and 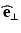 are unit vectors along the horizontal and vertical, respectively. In this case, the vibrational ellipse can be reformulated as
are unit vectors along the horizontal and vertical, respectively. In this case, the vibrational ellipse can be reformulated as
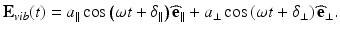
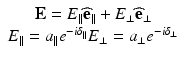
(33.7)
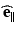 and
and 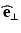 are unit vectors along the horizontal and vertical, respectively. In this case, the vibrational ellipse can be reformulated as
are unit vectors along the horizontal and vertical, respectively. In this case, the vibrational ellipse can be reformulated as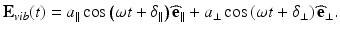
(33.8)
The overall irradiance, or intensity, of the beam of light then can be expressed as the scalar quantity
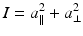
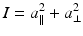
(33.9)
It is worth noting that while the overall irradiance of a beam is not dependent on its polarization state, it is possible to measure irradiance along a particular orientation (e.g., the intensity of a beam in the horizontal direction).
Linear polarization states occur for phase differences Δδ = δ ∥ − δ ⊥ = m π, where m ∈ ℤ, as the vibrational ellipse collapses to a line described by
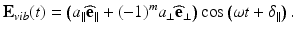
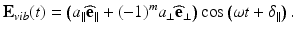
(33.10)
The orientation of the linear polarization state depends on the ratio of amplitudes a ∥ and a ⊥. The polarization state of light is horizontal or vertical when a ⊥ = 0 or a ∥ = 0, respectively, and oriented at ±45° if |a ∥| = |a ⊥|. An orientation angle θ can then be defined according to the relations:

where α can be thought of as an overall amplitude of the electric field and Δδ = 0.

(33.11)
Circular polarization states are obtained when |a ∥| = |a ⊥| and 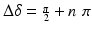 , which is evident through the form of the resultant vibrational ellipse:
, which is evident through the form of the resultant vibrational ellipse:
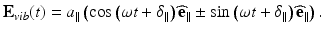
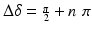 , which is evident through the form of the resultant vibrational ellipse:
, which is evident through the form of the resultant vibrational ellipse: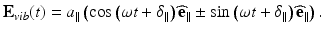
(33.12)
This describes a circle, the handedness (left or right circular) of which is determined by the sign between the orthogonal components. Circular polarization states differ only in their phase difference compared to linearly polarized light at 45°, and so the phase difference Δδ between orthogonal electric field components reflects the ratio between circular and linear components of the polarization state.
The electric field decomposition in Eq. 33.7 can be rewritten as a complex 2-vector such that
![$$ \mathbf{E}=\left[\begin{array}{c}\hfill {E}_{\parallel}\hfill \\ {}\hfill {E}_{\perp}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {a}_{\parallel }{e}^{-i{\delta}_{\parallel }}\hfill \\ {}\hfill {a}_{\perp }{e}^{-i{\delta}_{\perp }}\hfill \end{array}\right]=a\;{e}^{-i{\delta}_{\parallel }}\left[\begin{array}{c}\hfill \cos \theta \hfill \\ {}\hfill {e}^{i\;\Delta \delta } \sin \theta \hfill \end{array}\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ13.gif)
![$$ \mathbf{E}=\left[\begin{array}{c}\hfill {E}_{\parallel}\hfill \\ {}\hfill {E}_{\perp}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {a}_{\parallel }{e}^{-i{\delta}_{\parallel }}\hfill \\ {}\hfill {a}_{\perp }{e}^{-i{\delta}_{\perp }}\hfill \end{array}\right]=a\;{e}^{-i{\delta}_{\parallel }}\left[\begin{array}{c}\hfill \cos \theta \hfill \\ {}\hfill {e}^{i\;\Delta \delta } \sin \theta \hfill \end{array}\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ13.gif)
(33.13)
While the time-invariant electric field vector E, also known as a Jones vector, does depend on the amplitude and exact phase of the electric field components, it should be noted that the polarization state itself is completely determined by the orientation angle θ and the phase difference Δδ.
33.1.1.2 Jones Matrices
Just as two vectors of length n can be related using a matrix of dimension n × n, two polarization states can be related using a complex 2 × 2 matrix known as a Jones matrix. The polarization properties of any non-depolarizing optical system can be described using a Jones matrix. The transmitted polarization state E′ as a result of an optical system represented by a Jones matrix J acting on an incident polarization state E can be determined by
![$$ {\mathbf{E}}^{\mathbf{\prime}}=\left[\begin{array}{c}\hfill {E}_{\parallel}^{\prime}\hfill \\ {}\hfill {E}_{\perp}^{\prime}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill {J}_{11}\hfill & \hfill {J}_{12}\hfill \\ {}\hfill {J}_{21}\hfill & \hfill {J}_{22}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {E}_{\parallel}\hfill \\ {}\hfill {E}_{\perp}\hfill \end{array}\right]=\mathbf{J}\;\mathbf{E}. $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ14.gif)
![$$ {\mathbf{E}}^{\mathbf{\prime}}=\left[\begin{array}{c}\hfill {E}_{\parallel}^{\prime}\hfill \\ {}\hfill {E}_{\perp}^{\prime}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill {J}_{11}\hfill & \hfill {J}_{12}\hfill \\ {}\hfill {J}_{21}\hfill & \hfill {J}_{22}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {E}_{\parallel}\hfill \\ {}\hfill {E}_{\perp}\hfill \end{array}\right]=\mathbf{J}\;\mathbf{E}. $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ14.gif)
(33.14)
Subsequent transmission of E′ through an optical system J′ results in a polarization state E″ = J′ E′ = J′(J E) = J′J E. As a result, the combined polarization effect of a cascade of optical elements, J 1, J 2, ⋯, J n , can be described by the product J = J n ⋯ J 2 J 1.
The Jones matrix for a birefringent material that induces a phase retardation η between electric field components parallel and orthogonal to a polarization state characterized by an orientation angle θ and a circularity related to ϕ is given by [31]
![$$ {\mathbf{J}}_b=\left[\begin{array}{cc}\hfill {e}^{i\eta /2}{C}_{\theta}^2+{e}^{-i\eta /2}{S}_{\theta}^2\hfill & \hfill \left({e}^{i\eta /2}-{e}^{-i\eta /2}\right){C}_{\theta }{S}_{\theta }{e}^{-i\phi}\hfill \\ {}\hfill \left({e}^{i\eta /2}-{e}^{-i\eta /2}\right){C}_{\theta }{S}_{\theta }{e}^{i\phi}\hfill & \hfill {e}^{i\eta /2}{S}_{\theta}^2+{e}^{-i\eta /2}{C}_{\theta}^2\hfill \end{array}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ15.gif)
where C θ = cos θ and S θ = sin θ. The Jones matrix of a dichroic material with attenuation ratios of P 1 and P 2 for electric field components parallel and orthogonal, respectively, to a polarization state given by an orientation angle Θ and a circularity Φ has the form [31]
![$$ {\mathbf{J}}_d=\left[\begin{array}{cc}\hfill {P}_1{C}_{\Theta}^2+{P}_2{S}_{\Theta}^2\hfill & \hfill \left({P}_1-{P}_2\right){C}_{\Theta}{S}_{\Theta}{e}^{-i\Phi}\hfill \\ {}\hfill \left({P}_1-{P}_2\right){C}_{\Theta}{S}_{\Theta}{e}^{i\Phi}\hfill & \hfill {P}_1{S}_{\Theta}^2+{P}_2{C}_{\Theta}^2\hfill \end{array}\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ16.gif)
![$$ {\mathbf{J}}_b=\left[\begin{array}{cc}\hfill {e}^{i\eta /2}{C}_{\theta}^2+{e}^{-i\eta /2}{S}_{\theta}^2\hfill & \hfill \left({e}^{i\eta /2}-{e}^{-i\eta /2}\right){C}_{\theta }{S}_{\theta }{e}^{-i\phi}\hfill \\ {}\hfill \left({e}^{i\eta /2}-{e}^{-i\eta /2}\right){C}_{\theta }{S}_{\theta }{e}^{i\phi}\hfill & \hfill {e}^{i\eta /2}{S}_{\theta}^2+{e}^{-i\eta /2}{C}_{\theta}^2\hfill \end{array}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ15.gif)
(33.15)
![$$ {\mathbf{J}}_d=\left[\begin{array}{cc}\hfill {P}_1{C}_{\Theta}^2+{P}_2{S}_{\Theta}^2\hfill & \hfill \left({P}_1-{P}_2\right){C}_{\Theta}{S}_{\Theta}{e}^{-i\Phi}\hfill \\ {}\hfill \left({P}_1-{P}_2\right){C}_{\Theta}{S}_{\Theta}{e}^{i\Phi}\hfill & \hfill {P}_1{S}_{\Theta}^2+{P}_2{C}_{\Theta}^2\hfill \end{array}\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ16.gif)
(33.16)
33.1.1.3 Early Bulk-Optic PS-OCT Systems
Prior to 1992, the emphasis in OCT was the reconstruction of two-dimensional maps of tissue reflectivity while neglecting the polarization state of light. Hee et al. then presented an OCT system able to measure the changes in the polarization state of light reflected from a sample [6]. Using an incoherent detection technique, they demonstrated birefringence-sensitive ranging in a wave plate, an electro-optic modulator, and calf coronary artery. In 1997, the first two-dimensional images of birefringence were presented using a similar system, and the effect of laser-induced thermal damage on tissue birefringence in bovine tendon was demonstrated [7], followed in 1998 by a demonstration of the birefringence in porcine myocardium [8]. In 1999, phase-sensitive detection was implemented to determine the phase relation between the interference fringes in orthogonal polarization channels, which allowed for calculation of the Stokes parameters (Sect. 33.1.2.1) of the reflected light with a single measurement. Hitzenberger et al. used the phase relation in 2001 to determine the optic axis orientation of a birefringent sample [12].
The underlying theory behind extraction of the reflectivity and birefringence of a sample using these three bulk-optic PS-OCT systems will be discussed in the context of the Michelson interferometer presented by Hee et al. [6]. A schematic diagram of this early bulk-optic system is shown in Fig. 33.2. Collimated light with a short coherence length passes through a polarizer (Pol) to select a pure linear horizontal input state and is split into reference and sample arms by a polarization-insensitive beam splitter (BS). Light in the reference arm passes through a zero-order quarter-wave plate (QWP) oriented at 22.5°. Light in the sample arm passes through a QWP oriented at 45° and through focusing optics, producing circularly polarized light incident on the sample. Reflected light from the sample, in an arbitrary (elliptical) polarization state determined by the optical properties of the sample, returns through the focusing optics and the QWP. After recombination with light from the reference arm, the light in the detector arm is split into its horizontal and vertical components by a polarizing beam splitter (PBS) and detected separately (Fig. 33.3).

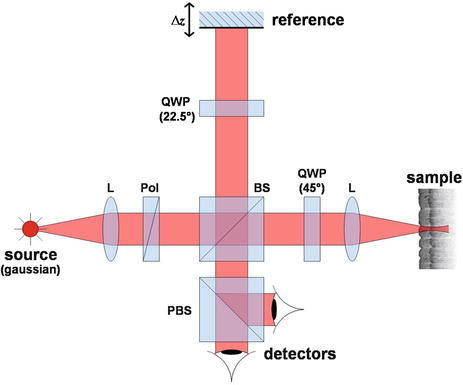

Fig. 33.2
Illustration of diattenuation (left) and birefringence (right). For diattenuation, the horizontal electric field component is attenuated more than the vertical component. The birefringent material on the right creates a phase delay between the horizontal and vertical electric field components

Fig. 33.3
Schematic of the bulk-optic PS-OCT system. The output of a source with a Gaussian spectrum is linearly polarized and split using a nonpolarizing beam splitter into sample and reference arms. The reference arm is composed of a quarter-wave plate (QWP) oriented at 22.5° and a mirror. The sample arm uses a QWP at 45° and a lens to focus light onto a sample. The reflected light from both arms is recombined and the resulting interference pattern is split using a polarizing beam splitter (PBS) onto two separate detectors. Individual axial scans are generated by translation of the reference arm mirror, and images are formed by combining axial scans for different lateral positions of the beam on the sample
The intensity detected in each polarization channel can be described by a two-dimensional intensity vector I, where the two components describe the horizontal and vertical polarized intensities. The intensities at the detectors are given by
![$$ \left\langle \mathbf{I}\left(\Delta z\right)\right\rangle =\left\langle \left[\begin{array}{c}\hfill {E}_{r\parallel }{E}_{r\parallel}^{\ast}\hfill \\ {}\hfill {E}_{r\perp }{E}_{r\perp}^{\ast}\hfill \end{array}\right]\right\rangle +\left\langle \left[\begin{array}{c}\hfill {E}_{s\parallel }{E}_{s\parallel}^{\ast}\hfill \\ {}\hfill {E}_{s\perp }{E}_{s\perp}^{\ast}\hfill \end{array}\right]\right\rangle +\left\langle \left[\begin{array}{c}\hfill {E}_{r\parallel }{E}_{s\parallel}^{\ast}\hfill \\ {}\hfill {E}_{r\perp }{E}_{s\perp}^{\ast}\hfill \end{array}\right]\right\rangle +\left\langle \left[\begin{array}{c}\hfill {E}_{s\parallel }{E}_{r\parallel}^{\ast}\hfill \\ {}\hfill {E}_{s\perp }{E}_{r\perp}^{\ast}\hfill \end{array}\right]\right\rangle, $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ17.gif)
where ![$$ {\mathbf{E}}_r={\left[\begin{array}{cc}\hfill {E}_{r\parallel },\hfill & \hfill {E}_{r\perp}\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq4.gif) and
and ![$$ {\mathbf{E}}_s={\left[\begin{array}{cc}\hfill {E}_{s\parallel },\hfill & \hfill {E}_{s\perp}\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq5.gif) are the Jones vector representations of light returning from the reference and sample arms, respectively, ∗ represents the complex conjugate, T is the transpose operation, and the angular brackets (〈 ⋯ 〉) denote time averaging. The last two terms of Eq. 33.17 correspond to the interference between reference and sample arm light.
are the Jones vector representations of light returning from the reference and sample arms, respectively, ∗ represents the complex conjugate, T is the transpose operation, and the angular brackets (〈 ⋯ 〉) denote time averaging. The last two terms of Eq. 33.17 correspond to the interference between reference and sample arm light.
![$$ \left\langle \mathbf{I}\left(\Delta z\right)\right\rangle =\left\langle \left[\begin{array}{c}\hfill {E}_{r\parallel }{E}_{r\parallel}^{\ast}\hfill \\ {}\hfill {E}_{r\perp }{E}_{r\perp}^{\ast}\hfill \end{array}\right]\right\rangle +\left\langle \left[\begin{array}{c}\hfill {E}_{s\parallel }{E}_{s\parallel}^{\ast}\hfill \\ {}\hfill {E}_{s\perp }{E}_{s\perp}^{\ast}\hfill \end{array}\right]\right\rangle +\left\langle \left[\begin{array}{c}\hfill {E}_{r\parallel }{E}_{s\parallel}^{\ast}\hfill \\ {}\hfill {E}_{r\perp }{E}_{s\perp}^{\ast}\hfill \end{array}\right]\right\rangle +\left\langle \left[\begin{array}{c}\hfill {E}_{s\parallel }{E}_{r\parallel}^{\ast}\hfill \\ {}\hfill {E}_{s\perp }{E}_{r\perp}^{\ast}\hfill \end{array}\right]\right\rangle, $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ17.gif)
(33.17)
![$$ {\mathbf{E}}_r={\left[\begin{array}{cc}\hfill {E}_{r\parallel },\hfill & \hfill {E}_{r\perp}\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq4.gif) and
and ![$$ {\mathbf{E}}_s={\left[\begin{array}{cc}\hfill {E}_{s\parallel },\hfill & \hfill {E}_{s\perp}\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq5.gif) are the Jones vector representations of light returning from the reference and sample arms, respectively, ∗ represents the complex conjugate, T is the transpose operation, and the angular brackets (〈 ⋯ 〉) denote time averaging. The last two terms of Eq. 33.17 correspond to the interference between reference and sample arm light.
are the Jones vector representations of light returning from the reference and sample arms, respectively, ∗ represents the complex conjugate, T is the transpose operation, and the angular brackets (〈 ⋯ 〉) denote time averaging. The last two terms of Eq. 33.17 correspond to the interference between reference and sample arm light.The polarizer in the source arm allows for full transmission of only horizontally polarized light and can therefore be parameterized with attenuation ratios P 1 = 1 and P 2 = 0 along and orthogonal to an orientation θ = 0. After the polarizer, horizontally polarized source light is described by the Jones vector
![$$ \mathbf{E}(z)=E(z)\left[\begin{array}{c}\hfill 1\hfill \\ {}\hfill 0\hfill \end{array}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ18.gif)
where  represents the integrated overall complex electric field amplitude of field amplitudes
represents the integrated overall complex electric field amplitude of field amplitudes 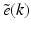 . From the Wiener–Khintchine theorem, it follows that
. From the Wiener–Khintchine theorem, it follows that
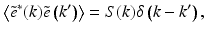
which defines 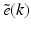 in terms of the source power spectral density S(k). The beam splitter divides the incident light by amplitude evenly between the sample and reference arms of the interferometer such that the Jones vectors describing the light entering each arm is given by
in terms of the source power spectral density S(k). The beam splitter divides the incident light by amplitude evenly between the sample and reference arms of the interferometer such that the Jones vectors describing the light entering each arm is given by
![$$ {\mathbf{E}}_{si}(z)={\mathbf{E}}_{ri}(z)=\frac{E(z)}{\sqrt{2}}\left[\begin{array}{c}\hfill 1\hfill \\ {}\hfill 0\hfill \end{array}\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ20.gif)
![$$ \mathbf{E}(z)=E(z)\left[\begin{array}{c}\hfill 1\hfill \\ {}\hfill 0\hfill \end{array}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ18.gif)
(33.18)
 represents the integrated overall complex electric field amplitude of field amplitudes
represents the integrated overall complex electric field amplitude of field amplitudes 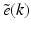 . From the Wiener–Khintchine theorem, it follows that
. From the Wiener–Khintchine theorem, it follows that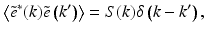
(33.19)
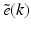 in terms of the source power spectral density S(k). The beam splitter divides the incident light by amplitude evenly between the sample and reference arms of the interferometer such that the Jones vectors describing the light entering each arm is given by
in terms of the source power spectral density S(k). The beam splitter divides the incident light by amplitude evenly between the sample and reference arms of the interferometer such that the Jones vectors describing the light entering each arm is given by![$$ {\mathbf{E}}_{si}(z)={\mathbf{E}}_{ri}(z)=\frac{E(z)}{\sqrt{2}}\left[\begin{array}{c}\hfill 1\hfill \\ {}\hfill 0\hfill \end{array}\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ20.gif)
(33.20)
The polarization state of light reflected from the reference arm can be calculated by multiplying E ri (z) by the Jones matrices of the optical elements in the reference optical path. A QWP aligned at 22.5° can be characterized by J b with η = π/2, η = π/8, and ϕ = 0, and so the reflection reference polarization state is given by
![$$ {\mathbf{E}}_r\left({z}_r\right)={\mathbf{J}}_b\left({\scriptscriptstyle \frac{\pi }{2}},{\scriptscriptstyle \frac{\pi }{8}},0\right){\mathbf{J}}_b\left({\scriptscriptstyle \frac{\pi }{2}},{\scriptscriptstyle \frac{\pi }{8}},0\right){\mathbf{E}}_{ri}={\scriptscriptstyle \frac{1}{2}}E\left(2{z}_r\right)\left[\begin{array}{c}\hfill 1\hfill \\ {}\hfill 1\hfill \end{array}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ21.gif)
where z r is the single-pass length of the reference arm. The horizontal and vertical components of the electric field have equal amplitude and phase. The polarization state of light returning from the sample arm can be computed similarly. In this case, the orientation of the QWP is 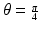 . Dichroism can generally be neglected for biological tissue, and the round-trip nature of light propagation in OCT cancels the effect of any circular birefringence. The measurable Jones matrix for a biological sample can then be modeled as a linearly birefringent material and can be written in the form
. Dichroism can generally be neglected for biological tissue, and the round-trip nature of light propagation in OCT cancels the effect of any circular birefringence. The measurable Jones matrix for a biological sample can then be modeled as a linearly birefringent material and can be written in the form  , with R(z) and
, with R(z) and  representing the scalar reflectivity and average phase delay of a wave propagating to some depth z,
representing the scalar reflectivity and average phase delay of a wave propagating to some depth z, 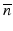 , and Δn representing the average and difference of the refractive indices along the parallel and orthogonal to the orientation of the material, α. The Jones vector of the light reflected from the sample arm is then given by
, and Δn representing the average and difference of the refractive indices along the parallel and orthogonal to the orientation of the material, α. The Jones vector of the light reflected from the sample arm is then given by
![$$ \begin{array}{l}{\mathbf{E}}_s\left({z}_s+z\right)={\mathbf{J}}_b\left({\scriptscriptstyle \frac{\pi }{2}},{\scriptscriptstyle \frac{\pi }{4}},0\right){\mathbf{J}}_S{\mathbf{J}}_b\left({\scriptscriptstyle \frac{\pi }{2}},{\scriptscriptstyle \frac{\pi }{4}},0\right)\\ {}\kern0.72em \propto \sqrt{R(z)}{\displaystyle \int \tilde{e}(k){e}^{-2ik\left({z}_s+z\overline{n}\right)}\left[\begin{array}{c}\hfill {e}^{2i\alpha } \sin \left(kz\Delta n\right)\hfill \\ {}\hfill \cos \left(kz\Delta n\right)\hfill \end{array}\right]dk}\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ22.gif)
where z s is the optical length of the arm up to the sample surface. Using the Wiener–Khintchine theorem, the interference terms in the horizontally and vertically polarized channels are
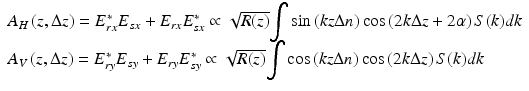
with z the depth in the tissue and 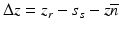 the optical path length difference between sample and reference arms. A Gaussian power spectral density is assumed for the source
the optical path length difference between sample and reference arms. A Gaussian power spectral density is assumed for the source

with a full width at half maximum (FWHM) spectral bandwidth given by 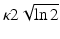 . The integration over k in Eq. 33.23 can be performed analytically and, in the approximation κzΔn ≪ 1, simplifies to
. The integration over k in Eq. 33.23 can be performed analytically and, in the approximation κzΔn ≪ 1, simplifies to
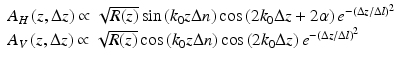
with the FWHM of the interference fringe envelope given by 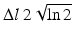 where
where
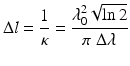
and Δλ is the spectral FWHM of the source in wavelength.
![$$ {\mathbf{E}}_r\left({z}_r\right)={\mathbf{J}}_b\left({\scriptscriptstyle \frac{\pi }{2}},{\scriptscriptstyle \frac{\pi }{8}},0\right){\mathbf{J}}_b\left({\scriptscriptstyle \frac{\pi }{2}},{\scriptscriptstyle \frac{\pi }{8}},0\right){\mathbf{E}}_{ri}={\scriptscriptstyle \frac{1}{2}}E\left(2{z}_r\right)\left[\begin{array}{c}\hfill 1\hfill \\ {}\hfill 1\hfill \end{array}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ21.gif)
(33.21)
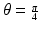 . Dichroism can generally be neglected for biological tissue, and the round-trip nature of light propagation in OCT cancels the effect of any circular birefringence. The measurable Jones matrix for a biological sample can then be modeled as a linearly birefringent material and can be written in the form
. Dichroism can generally be neglected for biological tissue, and the round-trip nature of light propagation in OCT cancels the effect of any circular birefringence. The measurable Jones matrix for a biological sample can then be modeled as a linearly birefringent material and can be written in the form  , with R(z) and
, with R(z) and  representing the scalar reflectivity and average phase delay of a wave propagating to some depth z,
representing the scalar reflectivity and average phase delay of a wave propagating to some depth z,  , and Δn representing the average and difference of the refractive indices along the parallel and orthogonal to the orientation of the material, α. The Jones vector of the light reflected from the sample arm is then given by
, and Δn representing the average and difference of the refractive indices along the parallel and orthogonal to the orientation of the material, α. The Jones vector of the light reflected from the sample arm is then given by![$$ \begin{array}{l}{\mathbf{E}}_s\left({z}_s+z\right)={\mathbf{J}}_b\left({\scriptscriptstyle \frac{\pi }{2}},{\scriptscriptstyle \frac{\pi }{4}},0\right){\mathbf{J}}_S{\mathbf{J}}_b\left({\scriptscriptstyle \frac{\pi }{2}},{\scriptscriptstyle \frac{\pi }{4}},0\right)\\ {}\kern0.72em \propto \sqrt{R(z)}{\displaystyle \int \tilde{e}(k){e}^{-2ik\left({z}_s+z\overline{n}\right)}\left[\begin{array}{c}\hfill {e}^{2i\alpha } \sin \left(kz\Delta n\right)\hfill \\ {}\hfill \cos \left(kz\Delta n\right)\hfill \end{array}\right]dk}\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ22.gif)
(33.22)
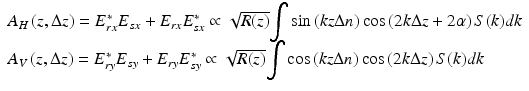
(33.23)
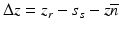 the optical path length difference between sample and reference arms. A Gaussian power spectral density is assumed for the source
the optical path length difference between sample and reference arms. A Gaussian power spectral density is assumed for the source
(33.24)
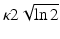 . The integration over k in Eq. 33.23 can be performed analytically and, in the approximation κzΔn ≪ 1, simplifies to
. The integration over k in Eq. 33.23 can be performed analytically and, in the approximation κzΔn ≪ 1, simplifies to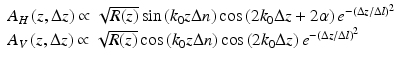
(33.25)
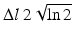 where
where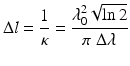
(33.26)
Demodulation of the signals eliminates the cos(2k 0Δz) terms in Eq. 33.25 to yield intensities in the horizontal and vertical polarization channels proportional to
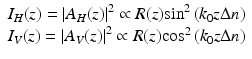
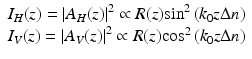
(33.27)
The total reflected intensity and phase retardation as functions of depth are given by


(33.28)
33.1.2 Mueller–Stokes Formalism
There are two weaknesses of the Jones formalism: the inability to describe partially polarized light and the inability to describe the processes that lead to depolarization. These shortcomings are addressed by Stokes parameters and Mueller matrices [25], which are quantities based on irradiance, a measure of the energy per unit area and time of a light beam. If two or more quasi-monochromatic beams propagating in the same directions are superposed incoherently, that is to say, there is no fixed relationship among the phases of the separate beams; the total irradiance is merely the sum of the individual beam irradiances. This property of irradiance makes it particularly attractive as a basis for an alternative way to describe polarization phenomena.
33.1.2.1 Stokes Parameters
Following the treatment in Bohren and Huffman [25], consider the following experimental setup to determine a set of irradiance measurements by which a polarization state can be completely characterized: a monochromatic beam, a set of perfect polarizers, and a detector capable of measuring irradiances regardless of polarization state. The simplest measurement is the overall irradiance of the beam. With no polarizer, the irradiance of the beam, ignoring the factor k/2ωμ 0, is given by E ∥ E ∥∗ + E ⊥ E ⊥∗. The simplest polarization characterization is to use horizontal and vertical linear polarizers to determine the difference in the irradiances of the horizontally and vertically polarized components of the beam given by E ∥ E ∥∗ − E ⊥ E ⊥∗. While these measurements immediately reveal the fraction of the overall beam irradiance due to horizontally and vertically polarized light, it reveals nothing regarding the phase between these elements. This can be overcome using linear polarizers oriented at +45° and −45° to measure E + E +∗ − E − E −∗, where 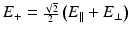 and
and  are the complex electric field component amplitudes in a basis spanned by light at +45° and –45° as defined by
are the complex electric field component amplitudes in a basis spanned by light at +45° and –45° as defined by 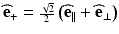 and
and 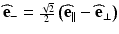 . Between these measurements, any completely linearly polarized beam can be fully characterized; however, light with any circularity cannot be characterized. Using circular polarizers to measure E R E R ∗ − E L E L ∗ then rounds out the characterization, where
. Between these measurements, any completely linearly polarized beam can be fully characterized; however, light with any circularity cannot be characterized. Using circular polarizers to measure E R E R ∗ − E L E L ∗ then rounds out the characterization, where 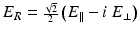 and
and 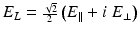 are the complex electric field component amplitudes in a basis spanned by right and left circularly polarized light as defined by
are the complex electric field component amplitudes in a basis spanned by right and left circularly polarized light as defined by 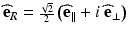 and
and  . These measurements can be summarized as follows:
. These measurements can be summarized as follows:
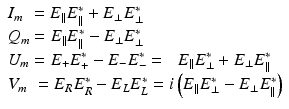
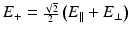 and
and  are the complex electric field component amplitudes in a basis spanned by light at +45° and –45° as defined by
are the complex electric field component amplitudes in a basis spanned by light at +45° and –45° as defined by 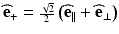 and
and 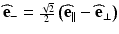 . Between these measurements, any completely linearly polarized beam can be fully characterized; however, light with any circularity cannot be characterized. Using circular polarizers to measure E R E R ∗ − E L E L ∗ then rounds out the characterization, where
. Between these measurements, any completely linearly polarized beam can be fully characterized; however, light with any circularity cannot be characterized. Using circular polarizers to measure E R E R ∗ − E L E L ∗ then rounds out the characterization, where 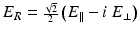 and
and 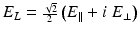 are the complex electric field component amplitudes in a basis spanned by right and left circularly polarized light as defined by
are the complex electric field component amplitudes in a basis spanned by right and left circularly polarized light as defined by 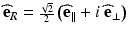 and
and  . These measurements can be summarized as follows:
. These measurements can be summarized as follows: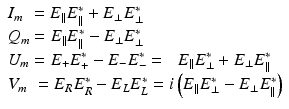
(33.29)
The polarization state of any monochromatic beam can be described using these four parameters (Fig. 33.4).
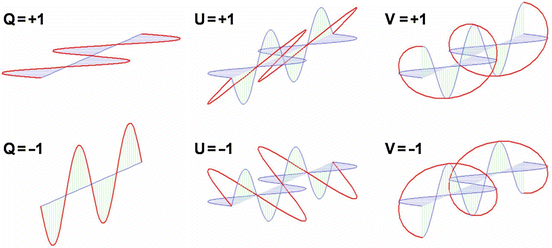

Fig. 33.4
Electric field components for various polarization states corresponding to the different Stokes parameters
The Stokes parameters can be used to describe a nearly monochromatic, or quasi-monochromatic, beam by simply taking time averages over an interval long compared with the period, such that
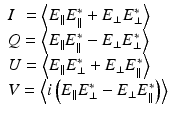
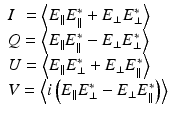
(33.30)
These quantities can be described by the notation s j , where s 0 = I, s 1 = Q, s 2 = U, and s 3 = V. Algebraic manipulation of the Stokes parameters leads to I 2 = Q 2 + U 2 + V 2 + 4(〈a ∥2〉〈a ⊥2〉 − 〈a ∥ a ⊥ e iδ 〉〈a ∥ a ⊥ e − iδ 〉) ≥ Q 2 + U 2 + V 2. Equality holds if the light is purely polarized; if the light is unpolarized, Q = U = V = 0. The degree of polarization P can now be defined by
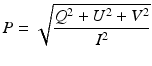
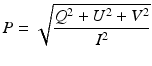
(33.31)
The degree of polarization of a beam of light can range from unity for purely polarized light to zero for unpolarized light.
Determination of Stokes Parameters in PS-OCT
The most direct method for measuring the Stokes parameters for light in a PS-OCT system is with a complete set of irradiance measurements (e.g., E ∥ E ∥∗, E ⊥ E ⊥∗, E + E +∗, etc.). This can be implemented with a set of polarizers and wave plates in the detection arm of an OCT interferometer. However, characterization of a polarization state would then require a multitude of measurements from any particular region of tissue. While sufficient for determining the polarization properties of a crystalline sample, this can be problematic for biological samples, especially for in vivo and clinical settings. Motion artifacts and other time constraints dictate that practical implementation of PS-OCT uses a minimum of measurements from any single location.
In 1999, de Boer et al. demonstrated a PS-OCT system that used phase-sensitive detection to determine the phase relation between the interference fringes in orthogonal polarization channels, which allowed for calculation of the Stokes parameters of the reflected light with a single measurement [10]. It is evident from Eq. 33.30 that all four Stokes parameters can be derived from phase-sensitive measurement of E ∥ and E ⊥ for light returning from a sample (as opposed to their corresponding irradiances). Using a system similar to that illustrated in Fig. 33.3, de Boer et al. utilized phase-sensitive detection of the interference fringe intensity for each polarization component to determine the complete Stokes parameters of light in a single measurement according to the relation [10]
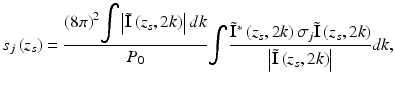
where 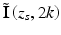 is a complex 2-vector representation of the components for positive k of the Fourier transform of the measured interference fringe intensities, σ 0 is the 2 × 2 identity matrix, and σ 1, σ 2, and σ 3 are the Pauli spin matrices.
is a complex 2-vector representation of the components for positive k of the Fourier transform of the measured interference fringe intensities, σ 0 is the 2 × 2 identity matrix, and σ 1, σ 2, and σ 3 are the Pauli spin matrices.
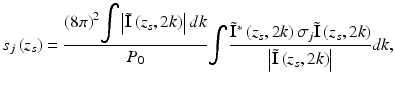
(33.32)
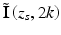 is a complex 2-vector representation of the components for positive k of the Fourier transform of the measured interference fringe intensities, σ 0 is the 2 × 2 identity matrix, and σ 1, σ 2, and σ 3 are the Pauli spin matrices.
is a complex 2-vector representation of the components for positive k of the Fourier transform of the measured interference fringe intensities, σ 0 is the 2 × 2 identity matrix, and σ 1, σ 2, and σ 3 are the Pauli spin matrices.It should be noted that an interferometric gating technique such as OCT measures only the light reflected from the sample arm that does interfere with the reference arm light. On first inspection, this suggests that the degree of polarization will always be unity, since only the coherent part of the reflected light is detected [17]. A closer inspection of Eq. 33.32 reveals that the Stokes parameters of each spectral component of the source are determined with a spectral resolution inversely proportional to the interval over which the Fourier transform was taken. Integration over the wave number k sums the Stokes parameters of each spectral component with a weight proportional to the power spectral density S(k). The larger the Δz interval and the higher the resolution in k-space, the more Stokes parameters of incoherently superposed beams are summed. When the Stokes parameters of reflected light do not vary over the source spectrum (the polarization state does not vary), the Stokes parameters add without changing the degree of polarization. However, when the Stokes parameters vary over the source spectrum, the sum of Stokes parameters over the spectral necessarily leads to an overall degree of polarization less than unity.
Rodent muscle was mounted in a chamber filled with saline solution and covered with a thin glass lip so that the muscle was not dehydrated during measurements. Figure 33.5 shows images of the four Stokes parameters in the sample frame for right circularly polarized incident light. Several periods of S 2 and S 3, cycling back and forth between 1 and −1, can be observed in the muscle.


Fig. 33.5
PS-OCT images of ex vivo rodent muscle, 1 × 1 mm, pixel size 10 × 10 μm. From left to right: the Stokes parameters (I); normalized parameters (Q, U, V) in the sample frame for right circularly polarized incident light; and the degree of polarization (P). The gray scale to the right gives the magnitude of the signal, 35 dB range for I, from 1 (white) to –1 (black) for Q, U, and V, and from 1 (white) to 0 (black) for P (Reprinted from Fig. 2 of Ref. [10] with permission of the Optical Society of America)
33.1.2.2 Mueller Matrices
The Stokes parameters can be written as a real 4-vector ![$$ \mathbf{S}={\left[\begin{array}{cccc}\hfill I,\hfill & \hfill Q,\hfill & \hfill U,\hfill & \hfill V\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq25.gif) , where I, Q, U, V ∈ ℝ. This allows for characterization of an optical system with a real 4 × 4 matrix M, known as a Mueller matrix, that relates an incident Stokes vector S to a transmitted Stokes vector S′ such that
, where I, Q, U, V ∈ ℝ. This allows for characterization of an optical system with a real 4 × 4 matrix M, known as a Mueller matrix, that relates an incident Stokes vector S to a transmitted Stokes vector S′ such that
![$$ {\mathbf{S}}^{\mathbf{\prime}}=\left[\begin{array}{c}\hfill {I}^{\prime}\hfill \\ {}\hfill {Q}^{\prime}\hfill \\ {}\hfill {U}^{\prime}\hfill \\ {}\hfill {V}^{\prime}\hfill \end{array}\right]=\left[\begin{array}{cccc}\hfill {M}_{11}\hfill & \hfill {M}_{12}\hfill & \hfill {M}_{13}\hfill & \hfill {M}_{14}\hfill \\ {}\hfill {M}_{21}\hfill & \hfill {M}_{22}\hfill & \hfill {M}_{23}\hfill & \hfill {M}_{24}\hfill \\ {}\hfill {M}_{31}\hfill & \hfill {M}_{32}\hfill & \hfill {M}_{33}\hfill & \hfill {M}_{34}\hfill \\ {}\hfill {M}_{41}\hfill & \hfill {M}_{42}\hfill & \hfill {M}_{43}\hfill & \hfill {M}_{44}\hfill \end{array}\right]\left[\begin{array}{c}\hfill I\hfill \\ {}\hfill Q\hfill \\ {}\hfill U\hfill \\ {}\hfill V\hfill \end{array}\right]=\mathbf{M}\;\mathbf{S} $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ33.gif)
![$$ \mathbf{S}={\left[\begin{array}{cccc}\hfill I,\hfill & \hfill Q,\hfill & \hfill U,\hfill & \hfill V\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq25.gif) , where I, Q, U, V ∈ ℝ. This allows for characterization of an optical system with a real 4 × 4 matrix M, known as a Mueller matrix, that relates an incident Stokes vector S to a transmitted Stokes vector S′ such that
, where I, Q, U, V ∈ ℝ. This allows for characterization of an optical system with a real 4 × 4 matrix M, known as a Mueller matrix, that relates an incident Stokes vector S to a transmitted Stokes vector S′ such that![$$ {\mathbf{S}}^{\mathbf{\prime}}=\left[\begin{array}{c}\hfill {I}^{\prime}\hfill \\ {}\hfill {Q}^{\prime}\hfill \\ {}\hfill {U}^{\prime}\hfill \\ {}\hfill {V}^{\prime}\hfill \end{array}\right]=\left[\begin{array}{cccc}\hfill {M}_{11}\hfill & \hfill {M}_{12}\hfill & \hfill {M}_{13}\hfill & \hfill {M}_{14}\hfill \\ {}\hfill {M}_{21}\hfill & \hfill {M}_{22}\hfill & \hfill {M}_{23}\hfill & \hfill {M}_{24}\hfill \\ {}\hfill {M}_{31}\hfill & \hfill {M}_{32}\hfill & \hfill {M}_{33}\hfill & \hfill {M}_{34}\hfill \\ {}\hfill {M}_{41}\hfill & \hfill {M}_{42}\hfill & \hfill {M}_{43}\hfill & \hfill {M}_{44}\hfill \end{array}\right]\left[\begin{array}{c}\hfill I\hfill \\ {}\hfill Q\hfill \\ {}\hfill U\hfill \\ {}\hfill V\hfill \end{array}\right]=\mathbf{M}\;\mathbf{S} $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ33.gif)
(33.33)
Since Stokes vectors can be used to describe depolarized and partially polarized light, Mueller matrices have the advantage over Jones matrices of being able to describe depolarization effects.
Vector and matrix quantities in the Jones formalism can be converted into Stokes parameters and Mueller matrices using the relations [25]
![$$ \begin{array}{l}\mathbf{S}=\left\langle \mathbf{U}\left(\mathbf{E}\otimes {\mathbf{E}}^{\ast}\right)\right\rangle \\ {}\mathbf{M}=\mathbf{U}\left(\mathbf{J}\otimes {\mathbf{J}}^{\ast}\right){\mathbf{U}}^{-1}\\ {}\mathbf{U}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ {}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \\ {}\hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill i\hfill & \hfill -i\hfill & \hfill 0\hfill \end{array}\right]\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ34.gif)
where ⊗ represents the Kronecker tensor product. The Mueller matrix for a partial polarizer (a dichroic material) M P can be formed from Eq. 33.16 to yield
![$$ {\mathbf{M}}_P=\left[\begin{array}{cccc}\hfill {q}_1\hfill & \hfill {q}_2{C}_{2\theta}\hfill & \hfill {q}_2{S}_{2\theta }{C}_{\phi}\hfill & \hfill {q}_2{S}_{2\theta }{S}_{\phi}\hfill \\ {}\hfill {q}_2{C}_{2\theta}\hfill & \hfill {q}_3+\left({q}_1-{q}_3\right){C}_{2\theta}^2\hfill & \hfill \left({q}_1-{q}_3\right){C}_{2\theta }{S}_{2\theta }{C}_{\phi}\hfill & \hfill \left({q}_1-{q}_3\right){C}_{2\theta }{S}_{2\theta }{S}_{\phi}\hfill \\ {}\hfill {q}_2{S}_{2\theta }{C}_{\phi}\hfill & \hfill \left({q}_1-{q}_3\right){C}_{2\theta }{S}_{2\theta }{C}_{\phi}\hfill & \hfill {q}_3+\left({q}_1-{q}_3\right){S}_{2\theta}^2{C}_{\phi}^2\hfill & \hfill \left({q}_1-{q}_3\right){S}_{2\theta}^2{C}_{\phi }{S}_{\phi}\hfill \\ {}\hfill {q}_2{S}_{2\theta }{S}_{\phi}\hfill & \hfill \left({q}_1-{q}_3\right){C}_{2\theta }{S}_{2\theta }{S}_{\phi}\hfill & \hfill \left({q}_1-{q}_3\right){S}_{2\theta}^2{C}_{\phi }{S}_{\phi}\hfill & \hfill {q}_3+\left({q}_1-{q}_3\right){S}_{2\theta}^2{S}_{\phi}^2\hfill \end{array}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ35.gif)
where 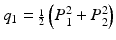 ,
, 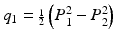 , and q 3 = P 1 P 2. The Mueller matrix for a retarder (a birefringent material) M R is given by
, and q 3 = P 1 P 2. The Mueller matrix for a retarder (a birefringent material) M R is given by
![$$ \begin{array}{l}{\mathbf{M}}_b=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill {C}_{\eta }+\left(1-{C}_{\eta}\right){C}_{2\Theta}^2\hfill \\ {}\hfill 0\hfill & \hfill {S}_{\eta }{S}_{2\Theta}{S}_{\Phi}+\left(1-{C}_{\eta}\right){C}_{2\Theta}{S}_{2\Theta}{C}_{\Phi}\hfill \\ {}\hfill 0\hfill & \hfill -{S}_{\eta }{S}_{2\Theta}{C}_{\Phi}+\left(1-{C}_{\eta}\right){C}_{2\Theta}{S}_{2\Theta}{S}_{\Phi}\hfill \end{array}\right.\\ {}\left.\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ {}\hfill -{S}_{\eta }{S}_{2\Theta}{S}_{\Phi}+\left(1-{C}_{\eta}\right){C}_{2\Theta}{S}_{2\Theta}{C}_{\Phi}\hfill & \hfill {S}_{\eta }{S}_{2\Theta}{C}_{\Phi}+\left(1-{C}_{\eta}\right){C}_{2\Theta}{S}_{2\Theta}{S}_{\Phi}\hfill \\ {}\hfill {C}_{\eta }+\left(1-{C}_{\eta}\right){S}_{2\Theta}^2{C}_{\Phi}^2\hfill & \hfill -{S}_{\eta }{C}_{2\Theta}+\left(1-{C}_{\eta}\right){S}_{2\Theta}^2{C}_{\Phi}{S}_{\Phi}\hfill \\ {}\hfill {S}_{\eta }{C}_{2\Theta}+\left(1-{C}_{\eta}\right){S}_{2\Theta}^2{C}_{\Phi}{S}_{\Phi}\hfill & \hfill {C}_{\eta }+\left(1-{C}_{\eta}\right){S}_{2\Theta}^2{S}_{\Phi}^2\hfill \end{array}\right]\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ36.gif)
![$$ \begin{array}{l}\mathbf{S}=\left\langle \mathbf{U}\left(\mathbf{E}\otimes {\mathbf{E}}^{\ast}\right)\right\rangle \\ {}\mathbf{M}=\mathbf{U}\left(\mathbf{J}\otimes {\mathbf{J}}^{\ast}\right){\mathbf{U}}^{-1}\\ {}\mathbf{U}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ {}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \\ {}\hfill 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill i\hfill & \hfill -i\hfill & \hfill 0\hfill \end{array}\right]\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ34.gif)
(33.34)
![$$ {\mathbf{M}}_P=\left[\begin{array}{cccc}\hfill {q}_1\hfill & \hfill {q}_2{C}_{2\theta}\hfill & \hfill {q}_2{S}_{2\theta }{C}_{\phi}\hfill & \hfill {q}_2{S}_{2\theta }{S}_{\phi}\hfill \\ {}\hfill {q}_2{C}_{2\theta}\hfill & \hfill {q}_3+\left({q}_1-{q}_3\right){C}_{2\theta}^2\hfill & \hfill \left({q}_1-{q}_3\right){C}_{2\theta }{S}_{2\theta }{C}_{\phi}\hfill & \hfill \left({q}_1-{q}_3\right){C}_{2\theta }{S}_{2\theta }{S}_{\phi}\hfill \\ {}\hfill {q}_2{S}_{2\theta }{C}_{\phi}\hfill & \hfill \left({q}_1-{q}_3\right){C}_{2\theta }{S}_{2\theta }{C}_{\phi}\hfill & \hfill {q}_3+\left({q}_1-{q}_3\right){S}_{2\theta}^2{C}_{\phi}^2\hfill & \hfill \left({q}_1-{q}_3\right){S}_{2\theta}^2{C}_{\phi }{S}_{\phi}\hfill \\ {}\hfill {q}_2{S}_{2\theta }{S}_{\phi}\hfill & \hfill \left({q}_1-{q}_3\right){C}_{2\theta }{S}_{2\theta }{S}_{\phi}\hfill & \hfill \left({q}_1-{q}_3\right){S}_{2\theta}^2{C}_{\phi }{S}_{\phi}\hfill & \hfill {q}_3+\left({q}_1-{q}_3\right){S}_{2\theta}^2{S}_{\phi}^2\hfill \end{array}\right], $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ35.gif)
(33.35)
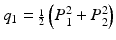 ,
, 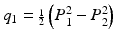 , and q 3 = P 1 P 2. The Mueller matrix for a retarder (a birefringent material) M R is given by
, and q 3 = P 1 P 2. The Mueller matrix for a retarder (a birefringent material) M R is given by![$$ \begin{array}{l}{\mathbf{M}}_b=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill {C}_{\eta }+\left(1-{C}_{\eta}\right){C}_{2\Theta}^2\hfill \\ {}\hfill 0\hfill & \hfill {S}_{\eta }{S}_{2\Theta}{S}_{\Phi}+\left(1-{C}_{\eta}\right){C}_{2\Theta}{S}_{2\Theta}{C}_{\Phi}\hfill \\ {}\hfill 0\hfill & \hfill -{S}_{\eta }{S}_{2\Theta}{C}_{\Phi}+\left(1-{C}_{\eta}\right){C}_{2\Theta}{S}_{2\Theta}{S}_{\Phi}\hfill \end{array}\right.\\ {}\left.\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ {}\hfill -{S}_{\eta }{S}_{2\Theta}{S}_{\Phi}+\left(1-{C}_{\eta}\right){C}_{2\Theta}{S}_{2\Theta}{C}_{\Phi}\hfill & \hfill {S}_{\eta }{S}_{2\Theta}{C}_{\Phi}+\left(1-{C}_{\eta}\right){C}_{2\Theta}{S}_{2\Theta}{S}_{\Phi}\hfill \\ {}\hfill {C}_{\eta }+\left(1-{C}_{\eta}\right){S}_{2\Theta}^2{C}_{\Phi}^2\hfill & \hfill -{S}_{\eta }{C}_{2\Theta}+\left(1-{C}_{\eta}\right){S}_{2\Theta}^2{C}_{\Phi}{S}_{\Phi}\hfill \\ {}\hfill {S}_{\eta }{C}_{2\Theta}+\left(1-{C}_{\eta}\right){S}_{2\Theta}^2{C}_{\Phi}{S}_{\Phi}\hfill & \hfill {C}_{\eta }+\left(1-{C}_{\eta}\right){S}_{2\Theta}^2{S}_{\Phi}^2\hfill \end{array}\right]\end{array} $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ36.gif)
(33.36)
Mueller Matrix Determination in PS-OCT
Yao et al. [11] and Jiao et al. [17] have presented a method by which the full Mueller matrix of a biological sample can be obtained. Their systems used variable wave plates and polarizers to sequentially obtain the four irradiance measurements I H = 〈E ∥ E ∥∗〉, I V = 〈E ⊥ E ⊥∗〉, I P = 〈E + E +∗〉, and I R = 〈E R E R ∗〉. Since the overall intensity of light has the property I = 〈E ∥ E ∥∗〉 + 〈E ⊥ E ⊥∗〉 = 〈E + E +∗〉 + 〈E − E −∗〉 = 〈E R E R ∗〉 + 〈E L E L ∗〉, the Stokes parameters will be given by
![$$ \mathbf{S}=\left[\begin{array}{c}\hfill {I}_H+{I}_V\hfill \\ {}\hfill {I}_H-{I}_V\hfill \\ {}\hfill 2{I}_P-\left({I}_H+{I}_V\right)\hfill \\ {}\hfill 2{I}_R-\left({I}_H+{I}_V\right)\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ37.gif)
![$$ \mathbf{S}=\left[\begin{array}{c}\hfill {I}_H+{I}_V\hfill \\ {}\hfill {I}_H-{I}_V\hfill \\ {}\hfill 2{I}_P-\left({I}_H+{I}_V\right)\hfill \\ {}\hfill 2{I}_R-\left({I}_H+{I}_V\right)\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ37.gif)
(33.37)
Acquisition of the reflected Stokes parameters for incident polarization states characterized by 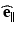 ,
, 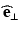 ,
, 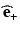 , and
, and 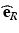 then yields sufficient information to completely determine the Mueller matrix of a sample. One disadvantage is that determination of a Mueller matrix requires a relatively large number of sequential measurements from any location in a sample. More importantly, this mathematically complete characterization can be difficult to interpret; decomposition of a given Mueller matrix [26, 27, 31] to yield useful parameterization of polarization effects can be difficult to obtain.
then yields sufficient information to completely determine the Mueller matrix of a sample. One disadvantage is that determination of a Mueller matrix requires a relatively large number of sequential measurements from any location in a sample. More importantly, this mathematically complete characterization can be difficult to interpret; decomposition of a given Mueller matrix [26, 27, 31] to yield useful parameterization of polarization effects can be difficult to obtain.
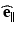 ,
, 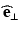 ,
, 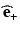 , and
, and 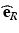 then yields sufficient information to completely determine the Mueller matrix of a sample. One disadvantage is that determination of a Mueller matrix requires a relatively large number of sequential measurements from any location in a sample. More importantly, this mathematically complete characterization can be difficult to interpret; decomposition of a given Mueller matrix [26, 27, 31] to yield useful parameterization of polarization effects can be difficult to obtain.
then yields sufficient information to completely determine the Mueller matrix of a sample. One disadvantage is that determination of a Mueller matrix requires a relatively large number of sequential measurements from any location in a sample. More importantly, this mathematically complete characterization can be difficult to interpret; decomposition of a given Mueller matrix [26, 27, 31] to yield useful parameterization of polarization effects can be difficult to obtain.A number of subsequent publications have also determined the Mueller matrix for a sample using faster systems with a more traditional two-channel detection scheme similar to that shown in Fig. 33.3 [19, 20, 32]. However, these studies compared the Jones vectors for light incident on and reflected back from a sample to first determine the sample Jones matrix, which is used to derive a corresponding Mueller matrix. The coherent detection of OCT and the nature of Jones vectors necessarily dictates that the degree of polarization be unity. Unless these calculations are performed in a wavelength-dependent manner, any resultant Mueller matrices can be used to only determine the non-depolarizing polarization properties of a sample, negating any potential advantage of the otherwise difficult-to-interpret Mueller matrix.
33.1.2.3 Poincaré Sphere
The Poincaré sphere is a three-dimensional representation of polarization states that allows for a more intuitive depiction of polarization phenomena. The Q-, U-, and V-components of the Stokes parameters are sufficient to describe the polarization state of light. For a partially polarized beam, the I-Stokes parameter additionally provides only the degree of polarization. In the case of a fully polarized beam, I 2 = Q 2 + U 2 + V 2. Thus, an explicit parameter to describe only the intensity of a beam is unnecessary, and the Stokes parameters can be expressed as a real 3-vector of the form
![$$ \overrightarrow{S}=\left[\begin{array}{c}\hfill Q\hfill \\ {}\hfill U\hfill \\ {}\hfill V\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ38.gif)
![$$ \overrightarrow{S}=\left[\begin{array}{c}\hfill Q\hfill \\ {}\hfill U\hfill \\ {}\hfill V\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ38.gif)
(33.38)
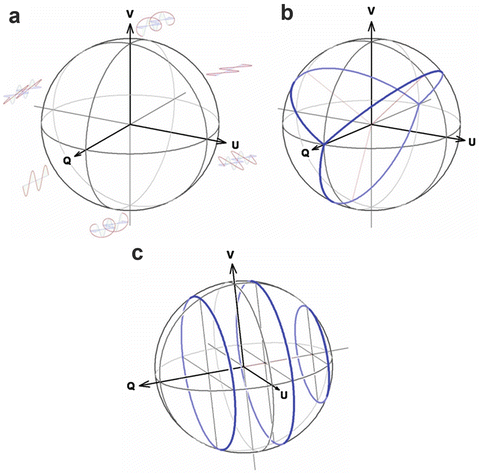
Such vectors can be pictured in a three-dimensional space known as a Poincaré sphere [33]. In the conventional Poincaré sphere notation, the direction of a polarization state is described by a vector ![$$ \overrightarrow{S}={\left[\begin{array}{ccc}\hfill q,\hfill & \hfill u,\hfill & \hfill v\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq32.gif) , where q = Q/I, u = U/I, and v = V/I. The radius of the sphere itself is unity, and the magnitude of a polarization state vector is defined by its degree of polarization. However, in discussions of purely polarized light, a modified Poincaré sphere can be more useful, where the Q-, U-, and V-parameters map to the x-, y-, and z-coordinates of a three-dimensional space. The radius of the sphere will be defined by I, and the degree of polarization will be ignored. It should be noted that the degree of polarization of light detected with optical coherence tomography can be less than unity [34]. The Poincaré sphere representation provides a convenient framework for visualizing polarization phenomenon by using the Q-, U-, and V-parameters as the x-, y-, and z-coordinates of a three-dimensional space (Fig. 33.6).
, where q = Q/I, u = U/I, and v = V/I. The radius of the sphere itself is unity, and the magnitude of a polarization state vector is defined by its degree of polarization. However, in discussions of purely polarized light, a modified Poincaré sphere can be more useful, where the Q-, U-, and V-parameters map to the x-, y-, and z-coordinates of a three-dimensional space. The radius of the sphere will be defined by I, and the degree of polarization will be ignored. It should be noted that the degree of polarization of light detected with optical coherence tomography can be less than unity [34]. The Poincaré sphere representation provides a convenient framework for visualizing polarization phenomenon by using the Q-, U-, and V-parameters as the x-, y-, and z-coordinates of a three-dimensional space (Fig. 33.6).
![$$ \overrightarrow{S}={\left[\begin{array}{ccc}\hfill q,\hfill & \hfill u,\hfill & \hfill v\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq32.gif) , where q = Q/I, u = U/I, and v = V/I. The radius of the sphere itself is unity, and the magnitude of a polarization state vector is defined by its degree of polarization. However, in discussions of purely polarized light, a modified Poincaré sphere can be more useful, where the Q-, U-, and V-parameters map to the x-, y-, and z-coordinates of a three-dimensional space. The radius of the sphere will be defined by I, and the degree of polarization will be ignored. It should be noted that the degree of polarization of light detected with optical coherence tomography can be less than unity [34]. The Poincaré sphere representation provides a convenient framework for visualizing polarization phenomenon by using the Q-, U-, and V-parameters as the x-, y-, and z-coordinates of a three-dimensional space (Fig. 33.6).
, where q = Q/I, u = U/I, and v = V/I. The radius of the sphere itself is unity, and the magnitude of a polarization state vector is defined by its degree of polarization. However, in discussions of purely polarized light, a modified Poincaré sphere can be more useful, where the Q-, U-, and V-parameters map to the x-, y-, and z-coordinates of a three-dimensional space. The radius of the sphere will be defined by I, and the degree of polarization will be ignored. It should be noted that the degree of polarization of light detected with optical coherence tomography can be less than unity [34]. The Poincaré sphere representation provides a convenient framework for visualizing polarization phenomenon by using the Q-, U-, and V-parameters as the x-, y-, and z-coordinates of a three-dimensional space (Fig. 33.6).
Fig. 33.6
(a) The Poincaré sphere with illustrations of the electric field representations of the major axes. (b, c) Poincaré spheres showing arcs of equal phase difference and equal amplitude ratio, respectively, between orthogonal electric field components
Polarization states with equal amplitude ratios and equal phase differences between orthogonal electric field components follow well-defined arcs in a Poincaré sphere representation. Using the definitions in Eq. 33.7, the Stokes 3-vector simplifies to
![$$ \overrightarrow{S}=\left[\begin{array}{c}\hfill {a}_{\parallel}^2-{a}_{\perp}^2\hfill \\ {}\hfill 2{a}_{\parallel }{a}_{\perp }{C}_{\Delta \delta}\hfill \\ {}\hfill 2{a}_{\parallel }{a}_{\perp }{S}_{\Delta \delta}\hfill \end{array}\right]=\left({a}_{\parallel}^2+{a}_{\perp}^2\right)\left[\begin{array}{c}\hfill {C}_{\alpha}\hfill \\ {}\hfill {S}_{\alpha }{C}_{\Delta \delta}\hfill \\ {}\hfill {S}_{\alpha }{S}_{\Delta \delta}\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ39.gif)
where α is governed by the amplitude ratio such that C α = (a ∥2 − a ⊥2)/(a ∥2 + a ⊥2) and S α = 2a ∥ a ⊥/(a ∥2 + a ⊥2). It becomes evident that polarization states of equal amplitude ratio and equal phase difference between orthogonal electric field components trace latitude and longitude lines, respectively, where the Q -axis of the Poincaré sphere is treated as the pole.
![$$ \overrightarrow{S}=\left[\begin{array}{c}\hfill {a}_{\parallel}^2-{a}_{\perp}^2\hfill \\ {}\hfill 2{a}_{\parallel }{a}_{\perp }{C}_{\Delta \delta}\hfill \\ {}\hfill 2{a}_{\parallel }{a}_{\perp }{S}_{\Delta \delta}\hfill \end{array}\right]=\left({a}_{\parallel}^2+{a}_{\perp}^2\right)\left[\begin{array}{c}\hfill {C}_{\alpha}\hfill \\ {}\hfill {S}_{\alpha }{C}_{\Delta \delta}\hfill \\ {}\hfill {S}_{\alpha }{S}_{\Delta \delta}\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ39.gif)
(33.39)
The Jones matrices describing diattenuation and birefringence both fit the general form
![$$ \mathbf{J}=\left[\begin{array}{cc}\hfill X{C}_{\theta}^2+Y{S}_{\theta}^2\hfill & \hfill \left(X-Y\right){C}_{\theta }{S}_{\theta }{e}^{-i\phi}\hfill \\ {}\hfill \left(X-Y\right){C}_{\theta }{S}_{\theta }{e}^{i\phi}\hfill & \hfill X{S}_{\theta}^2+Y{C}_{\theta}^2\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ40.gif)
where X and Y are parameters defining the magnitude of polarization effects about an optic axis defined by θ and ϕ. For diattenuation, the general parameters take the form X = P 1 and Y = P 2, and in the case of birefringence, X = e iη/2 and Y = e − iη/2. For simultaneous birefringence and diattenuation about a common axis, X = P 1 e iη/2 and Y = P 2 e − iη/2. The transmitted state ![$$ {\mathbf{S}}^{\mathbf{\prime}}={\left[\begin{array}{cccc}\hfill {I}^{\prime },\hfill & \hfill {Q}^{\prime },\hfill & \hfill {U}^{\prime },\hfill & \hfill {V}^{\prime}\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq33.gif) is the product of the equivalent Mueller matrix M and the incident polarization state
is the product of the equivalent Mueller matrix M and the incident polarization state ![$$ \mathbf{S}={\left[\begin{array}{cccc}\hfill I,\hfill & \hfill Q,\hfill & \hfill U,\hfill & \hfill V\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq34.gif) . If no depolarization takes place, all such transformations can be completely described by the lower-right 3 × 3 sub-matrix of M. This reduction of the Mueller matrix allows for examination of the 3-vector equivalents of the transmitted and incident states,
. If no depolarization takes place, all such transformations can be completely described by the lower-right 3 × 3 sub-matrix of M. This reduction of the Mueller matrix allows for examination of the 3-vector equivalents of the transmitted and incident states, 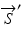 and
and 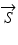 , in terms of polarization parameters X and Y and optic axis
, in terms of polarization parameters X and Y and optic axis ![$$ \overrightarrow{A}={\left[\begin{array}{ccc}\hfill {C}_{2\theta },\hfill & \hfill {S}_{2\theta }{C}_{\phi },\hfill & \hfill {S}_{2\theta }{S}_{\phi}\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq37.gif) , yielding the relation [35]
, yielding the relation [35]
![$$ \mathbf{J}=\left[\begin{array}{cc}\hfill X{C}_{\theta}^2+Y{S}_{\theta}^2\hfill & \hfill \left(X-Y\right){C}_{\theta }{S}_{\theta }{e}^{-i\phi}\hfill \\ {}\hfill \left(X-Y\right){C}_{\theta }{S}_{\theta }{e}^{i\phi}\hfill & \hfill X{S}_{\theta}^2+Y{C}_{\theta}^2\hfill \end{array}\right] $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_Equ40.gif)
(33.40)
![$$ {\mathbf{S}}^{\mathbf{\prime}}={\left[\begin{array}{cccc}\hfill {I}^{\prime },\hfill & \hfill {Q}^{\prime },\hfill & \hfill {U}^{\prime },\hfill & \hfill {V}^{\prime}\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq33.gif) is the product of the equivalent Mueller matrix M and the incident polarization state
is the product of the equivalent Mueller matrix M and the incident polarization state ![$$ \mathbf{S}={\left[\begin{array}{cccc}\hfill I,\hfill & \hfill Q,\hfill & \hfill U,\hfill & \hfill V\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq34.gif) . If no depolarization takes place, all such transformations can be completely described by the lower-right 3 × 3 sub-matrix of M. This reduction of the Mueller matrix allows for examination of the 3-vector equivalents of the transmitted and incident states,
. If no depolarization takes place, all such transformations can be completely described by the lower-right 3 × 3 sub-matrix of M. This reduction of the Mueller matrix allows for examination of the 3-vector equivalents of the transmitted and incident states, 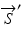 and
and 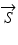 , in terms of polarization parameters X and Y and optic axis
, in terms of polarization parameters X and Y and optic axis ![$$ \overrightarrow{A}={\left[\begin{array}{ccc}\hfill {C}_{2\theta },\hfill & \hfill {S}_{2\theta }{C}_{\phi },\hfill & \hfill {S}_{2\theta }{S}_{\phi}\hfill \end{array}\right]}^T $$](/wp-content/uploads/2017/03/A76297_2_En_34_Chapter_IEq37.gif) , yielding the relation [35]
, yielding the relation [35]



