(41.1)
where k i and k s are wave vectors of incoming and scattered light, respectively, and v is the velocity vector of the moving particle (Fig. 41.1). Since Doppler OCT measures the backscattered light, assuming the angle between flow and sampling beam is θ, the Doppler shift equation is simplified to
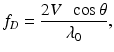
(41.2)
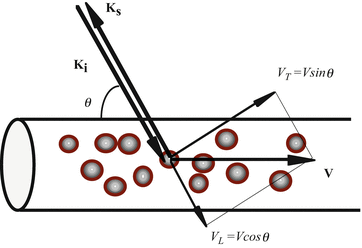
Fig. 41.1
Schematic of flow direction and probe beam angle
The optical system of Doppler OCT is similar to that of OCT. The primary difference is in signal processing. Figure 41.2 illustrates a Doppler OCT instrument that uses a fiber-optic Michelson interferometer with a broadband light as a source. Light from a broadband partially coherent source is coupled into a fiber interferometer by a 2 × 2 fiber coupler and then split equally into reference and sample arms of the interferometer. Light backscattered from the turbid sample is coupled back into the fiber and forms interference fringes with the light reflected from the reference arm. A rapid-scanning optical delay line is used for group delay and axial scanning. Because this delay line can decouple the group delay from the phase delay, an electro-optical phase modulator is introduced to produce a stable carrier frequency. The interference fringe intensity signal is amplified, band pass filtered, and digitized with a high-speed analog-to-digital converter. The signal processing is carried out at the same time as data is transferred to the computer, and real-time display can be accomplished by use of a digital signal processing board.
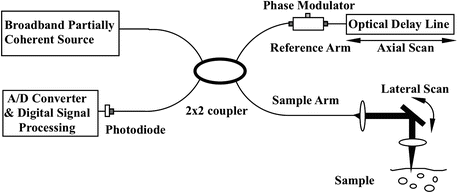

Fig. 41.2
Schematic of OCT system consisting of a fiber-based Michelson interferometer with a partially coherent light source
To understand the signal processing of Doppler OCT, let us look at the fringe signal due to the moving particles. If we denote U(t) as a complex-valued analytic signal of a stochastic process representing the field amplitude emitted by a low coherent light source and 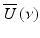 as the corresponding spectral amplitude at optical frequency ν, the amplitude of a partially coherent source light coupled into the interferometer at time t is written as a harmonic superposition
as the corresponding spectral amplitude at optical frequency ν, the amplitude of a partially coherent source light coupled into the interferometer at time t is written as a harmonic superposition
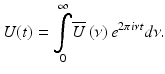
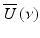 as the corresponding spectral amplitude at optical frequency ν, the amplitude of a partially coherent source light coupled into the interferometer at time t is written as a harmonic superposition
as the corresponding spectral amplitude at optical frequency ν, the amplitude of a partially coherent source light coupled into the interferometer at time t is written as a harmonic superposition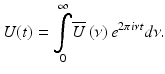
(41.3)
Because the stochastic process of a partially coherent light source is stationary, the cross-spectral density of 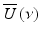 satisfies
satisfies
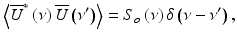
where S o (ν) is the source power spectral density and δ(ν − ν′) is the Dirac delta function. Assuming that light couples equally into the reference arm and sample arm with spectral amplitude of 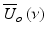 , the light coupled back to the detector from the reference,
, the light coupled back to the detector from the reference, 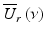 , and sample,
, and sample, 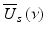 , are
, are
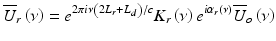
and
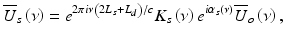
where L r and L s are the optical pathlengths from the beam splitter to the reference mirror and sample, respectively; L d is the optical pathlength from the beam splitter to the detector; and K r (ν)e iαr(ν) and K s (ν)e iαs(ν) are the amplitude reflection coefficients of light backscattered from the reference mirror and turbid sample, respectively.
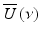 satisfies
satisfies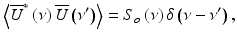
(41.4)
 , the light coupled back to the detector from the reference,
, the light coupled back to the detector from the reference,  , and sample,
, and sample, 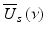 , are
, are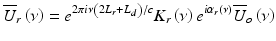
(41.5)
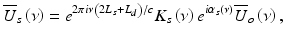
(41.6)
The total power detected at the interferometer output is given by a time-average of the squared light amplitude
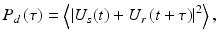
where τ is the time delay between light traveled in the sample and reference arms. Combining harmonic expansions for U s (t) and U r (t) and applying Eq. 41.4 when calculating the time-average, total power detected is a sum of three terms representing reference I r , sample I s , and the interference fringe intensity Γ ODT (τ),
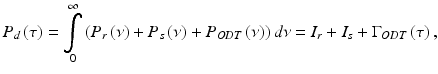
with
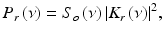
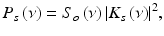
![$$ {P}_{ODT}\left(\nu \right)=2{S}_o\left(\nu \right){K}_r\left(\nu \right){K}_s\left(\nu \right) \cos \left[2\pi \nu \left({\Delta}_d/c+\tau \right)+{\alpha}_s\left(\nu \right)-{\alpha}_r\left(\nu \right)\right], $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ11.gif)
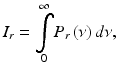
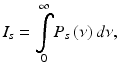
and
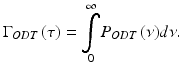
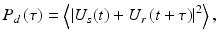
(41.7)
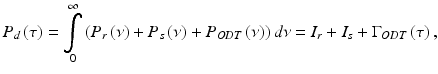
(41.8)
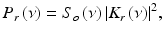
(41.9)
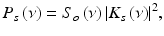
(41.10)
![$$ {P}_{ODT}\left(\nu \right)=2{S}_o\left(\nu \right){K}_r\left(\nu \right){K}_s\left(\nu \right) \cos \left[2\pi \nu \left({\Delta}_d/c+\tau \right)+{\alpha}_s\left(\nu \right)-{\alpha}_r\left(\nu \right)\right], $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ11.gif)
(41.11)
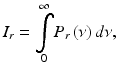
(41.12)
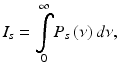
(41.13)
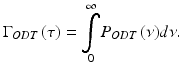
(41.14)
When there is a moving particle, light scattered from a moving particle is equivalent to a moving phase front; therefore, Δ d in Eq. 41.11 can be written as
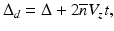
where Δ is the optical pathlength difference between light in the sample and reference arms, V z is the velocity of a moving particle parallel to the probe beam, and 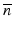 is the refractive index of flow media.
is the refractive index of flow media.
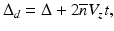
(41.15)
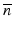 is the refractive index of flow media.
is the refractive index of flow media.To simplify the computation, we assume α s and α r are constants over the source spectrum and can be neglected. The spectral domain fringe signal, P ODT (ν), is simplified to
![$$ {P}_{ODT}\left(\nu \right)=2{S}_o\left(\nu \right){K}_r\left(\nu \right){K}_s\left(\nu \right) \cos \left[2\pi \nu \left(\left(\Delta +2\overline{n}{V}_zt\right)/c+\tau \right)\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ16.gif)
![$$ {P}_{ODT}\left(\nu \right)=2{S}_o\left(\nu \right){K}_r\left(\nu \right){K}_s\left(\nu \right) \cos \left[2\pi \nu \left(\left(\Delta +2\overline{n}{V}_zt\right)/c+\tau \right)\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ16.gif)
(41.16)
The corresponding time domain signal, Γ ODT (τ), is given by
![$$ {\Gamma}_{ODT}\left(\tau \right)=2{\displaystyle \underset{0}{\overset{\infty }{\int }}{S}_o\left(\nu \right){K}_r\left(\nu \right){K}_s\left(\nu \right) \cos \left[2\pi \nu \left(\left(\Delta +2\overline{n}{V}_zt\right)/c+\tau \right)\right]}d\nu . $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ17.gif)
![$$ {\Gamma}_{ODT}\left(\tau \right)=2{\displaystyle \underset{0}{\overset{\infty }{\int }}{S}_o\left(\nu \right){K}_r\left(\nu \right){K}_s\left(\nu \right) \cos \left[2\pi \nu \left(\left(\Delta +2\overline{n}{V}_zt\right)/c+\tau \right)\right]}d\nu . $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ17.gif)
(41.17)
A comparison of Eqs. 41.16 and 41.17 shows that there is a Fourier transformation relation between spectral domain and time domain signals. Consequently, there are two methods to acquire the Doppler OCT signal: the time-domain method and the Fourier-domain method.
In the time-domain method, a delay line is incorporated in the reference arm to generate a delay. A spectrogram analysis or phase-resolved algorithm is then used to determine the Doppler frequency shift. In the Fourier-domain method, the reference mirror is fixed, and there is no depth scan (τ = constant). The Fourier-domain fringe signal, P ODT (ν), is obtained either by a spectrometer at the detection arm or by a frequency sweeping light source. The time domain signal, Γ ODT (τ), is determined from the Fourier-domain signal by a Fourier transformation.
41.2.1 Phase-Resolved Doppler OCT Method
The first two-dimensional in vivo Doppler OCT imaging was reported using the spectrogram method [6, 7]. Researchers used the spectrogram method based on either short time fast Fourier transformation (STFFT) or wavelet transformation to determine the power spectrum of the measured fringe signal [5–7, 11, 71]. Although spectrogram methods allow simultaneous imaging of in vivo tissue structure and flow velocity, the velocity sensitivity is limited for high-speed imaging. When STFFT or wavelet transformation is used to calculate flow velocity, the resolution is determined by the window size of the Fourier transformation for each pixel. The minimum detectable Doppler frequency shift, f D , varies inversely with the STFFT window size. Because pixel acquisition time is proportional to the STFFT window size, the image frame rate is limited by velocity resolution. Furthermore, spatial resolution is also proportional to the STFFT window size. Therefore, a large STFFT window size increases velocity resolution while decreasing imaging speed and spatial resolution. This coupling between velocity sensitivity, spatial resolution, and imaging speed prevents the spectrogram method from achieving simultaneously both high imaging speed and high velocity sensitivity which are essential for measuring flow in small blood vessels where flow velocity is low.
Phase-resolved Doppler OCT overcomes the compromise between velocity sensitivity and imaging speed by using the phase change between sequential scans to construct flow velocity images [12]. The phase information of the fringe signal can be determined from the complex analytical signal 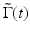 , which is determined through analytic continuation of the measured interference fringe function, Γ(t), using a Hilbert transformation [10]:
, which is determined through analytic continuation of the measured interference fringe function, Γ(t), using a Hilbert transformation [10]:
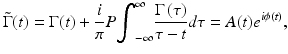
where P denotes the Cauchy principle value, i is the complex number, and A(t) and ϕ(t) are amplitude and phase term of 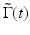 , respectively. Because the interference signal Γ(t) is quasi-monochromatic, the complex analytical signal can be determined by
, respectively. Because the interference signal Γ(t) is quasi-monochromatic, the complex analytical signal can be determined by
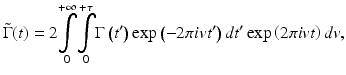
where τ is the time duration of the fringe signal in each axial scan.
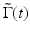 , which is determined through analytic continuation of the measured interference fringe function, Γ(t), using a Hilbert transformation [10]:
, which is determined through analytic continuation of the measured interference fringe function, Γ(t), using a Hilbert transformation [10]: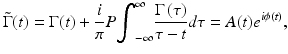
(41.18)
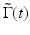 , respectively. Because the interference signal Γ(t) is quasi-monochromatic, the complex analytical signal can be determined by
, respectively. Because the interference signal Γ(t) is quasi-monochromatic, the complex analytical signal can be determined by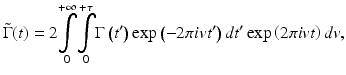
(41.19)
The Doppler frequency shift f n at n’th pixel in the axial direction is determined from the average phase shift between sequential A-scans. This can be accomplished by calculating the phase change of sequential scans from the individual analytical fringe signal:
![$$ {f}_n=\frac{\Delta \phi }{2\pi T}=\frac{1}{2\pi T}{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}{\displaystyle \sum_{j=1}^N}}\ \left[\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}\left(\frac{\mathrm{Im}{\tilde{\Gamma}}_{j+1}\left({t}_m\right)}{\mathrm{Re}{\tilde{\Gamma}}_{j+1}\left({t}_m\right)}\right)-\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}\left(\frac{\mathrm{Im}{\tilde{\Gamma}}_j\left({t}_m\right)}{\mathrm{Re}{\tilde{\Gamma}}_j\left({t}_m\right)}\right)\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ20.gif)
![$$ {f}_n=\frac{\Delta \phi }{2\pi T}=\frac{1}{2\pi T}{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}{\displaystyle \sum_{j=1}^N}}\ \left[\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}\left(\frac{\mathrm{Im}{\tilde{\Gamma}}_{j+1}\left({t}_m\right)}{\mathrm{Re}{\tilde{\Gamma}}_{j+1}\left({t}_m\right)}\right)-\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}\left(\frac{\mathrm{Im}{\tilde{\Gamma}}_j\left({t}_m\right)}{\mathrm{Re}{\tilde{\Gamma}}_j\left({t}_m\right)}\right)\right]. $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ20.gif)
(41.20)
Alternatively, the phase change can also be calculated by the cross-correlation method:
![$$ {f}_n=\frac{1}{2\pi T}\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}\left(\frac{\mathrm{Im}\ \left[{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N{\tilde{\Gamma}}_j\left({t}_m\right)\cdot {\tilde{\Gamma}}_{j+1}^{\ast}\left({t}_m\right)}\right]}{\mathrm{Re}\ \left[{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N{\tilde{\Gamma}}_j\left({t}_m\right)\cdot {\tilde{\Gamma}}_{j+1}^{\ast}\left({t}_m\right)}\right]}\right), $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ21.gif)
where 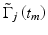 and
and 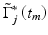 are the complex signals at axial time t m corresponding to the j’th A-scan and its respective conjugate,
are the complex signals at axial time t m corresponding to the j’th A-scan and its respective conjugate, 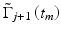 and
and 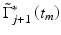 are the complex signals at axial time t m corresponding to the next A-scan and its respective conjugate, M is an even number that denotes the window size in the axial direction for each pixel, N is the number of sequential scans used to calculate the cross correlation, and T is the time duration between A-scans. Because T is much longer than the pixel time window within each scan used in the spectrogram method, high velocity sensitivity can be achieved.
are the complex signals at axial time t m corresponding to the next A-scan and its respective conjugate, M is an even number that denotes the window size in the axial direction for each pixel, N is the number of sequential scans used to calculate the cross correlation, and T is the time duration between A-scans. Because T is much longer than the pixel time window within each scan used in the spectrogram method, high velocity sensitivity can be achieved.
![$$ {f}_n=\frac{1}{2\pi T}\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}\left(\frac{\mathrm{Im}\ \left[{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N{\tilde{\Gamma}}_j\left({t}_m\right)\cdot {\tilde{\Gamma}}_{j+1}^{\ast}\left({t}_m\right)}\right]}{\mathrm{Re}\ \left[{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N{\tilde{\Gamma}}_j\left({t}_m\right)\cdot {\tilde{\Gamma}}_{j+1}^{\ast}\left({t}_m\right)}\right]}\right), $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ21.gif)
(41.21)
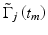 and
and 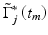 are the complex signals at axial time t m corresponding to the j’th A-scan and its respective conjugate,
are the complex signals at axial time t m corresponding to the j’th A-scan and its respective conjugate, 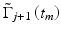 and
and 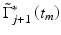 are the complex signals at axial time t m corresponding to the next A-scan and its respective conjugate, M is an even number that denotes the window size in the axial direction for each pixel, N is the number of sequential scans used to calculate the cross correlation, and T is the time duration between A-scans. Because T is much longer than the pixel time window within each scan used in the spectrogram method, high velocity sensitivity can be achieved.
are the complex signals at axial time t m corresponding to the next A-scan and its respective conjugate, M is an even number that denotes the window size in the axial direction for each pixel, N is the number of sequential scans used to calculate the cross correlation, and T is the time duration between A-scans. Because T is much longer than the pixel time window within each scan used in the spectrogram method, high velocity sensitivity can be achieved.In addition to the local velocity information, the standard deviation of the Doppler spectrum gives the variance of local velocity and can be determined from the measured analytical fringe signal:
![$$ {\sigma}^2=\frac{{\displaystyle {\int}_{-\infty}^{\infty }{\left(f-{f}_D\right)}^2P(f)df}}{{\displaystyle {\int}_{-\infty}^{\infty }P(f)df}}=\frac{1}{{\left(2\pi T\right)}^2}\left(1-\frac{\left|{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N{\tilde{\Gamma}}_j\left({t}_m\right)\cdot {\tilde{\Gamma}}_{j+1}^{\ast}\left({t}_m\right)}\right|}{\frac{1}{2}{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N\left[{\tilde{\Gamma}}_j\left({t}_m\right)\cdot {\tilde{\Gamma}}_j^{\ast}\left({t}_m\right)+{\tilde{\Gamma}}_{j+1}\left({t}_m\right)\cdot {\tilde{\Gamma}}_{j+1}^{\ast}\left({t}_m\right)\right]}}\right), $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ22.gif)
where P(f) is the Doppler power spectrum and f D is the centroid value of the Doppler frequency shift. The σ value depends on the flow velocity distribution. Variations in flow velocity will broaden the Doppler frequency spectrum and result in a large σ value. Thus, the Doppler variance image can be an indicator of flow variations and can be used to study flow turbulences. In addition, Doppler variance imaging can also be used to map microvasculature because it is less sensitive to the random direction and the pulsatile nature of blood flow in small vessels [22, 28]. Finally, standard deviation imaging can also be used to determine the transverse flow velocity [13].
![$$ {\sigma}^2=\frac{{\displaystyle {\int}_{-\infty}^{\infty }{\left(f-{f}_D\right)}^2P(f)df}}{{\displaystyle {\int}_{-\infty}^{\infty }P(f)df}}=\frac{1}{{\left(2\pi T\right)}^2}\left(1-\frac{\left|{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N{\tilde{\Gamma}}_j\left({t}_m\right)\cdot {\tilde{\Gamma}}_{j+1}^{\ast}\left({t}_m\right)}\right|}{\frac{1}{2}{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N\left[{\tilde{\Gamma}}_j\left({t}_m\right)\cdot {\tilde{\Gamma}}_j^{\ast}\left({t}_m\right)+{\tilde{\Gamma}}_{j+1}\left({t}_m\right)\cdot {\tilde{\Gamma}}_{j+1}^{\ast}\left({t}_m\right)\right]}}\right), $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ22.gif)
(41.22)
Phase-resolved Doppler OCT decouples spatial resolution and velocity sensitivity in flow images and increases imaging speed by more than two orders of magnitude without compromising spatial resolution and velocity sensitivity. In addition, because two sequential A-line scans are compared at the same location, speckle modulations in the fringe signals cancel each other and, therefore, will not affect the phase difference calculation. Consequently, the phase-resolved method reduces the speckle noise in the velocity image.
41.2.2 Fourier-Domain Phase-Resolved Doppler OCT Method
Compared with conventional time domain OCT, which is based on a scanning optical delay line, Fourier-domain OCT measures interference fringes in the spectral domain to reconstruct a tomographic image. Modulation of the interference fringe intensity in the spectral domain is used to determine the locations of all scattering objects along the beam propagation direction by a Fourier transformation. Two methods have been developed to employ the Fourier-domain technique: a spectrometer based system that uses a high-speed line-scan camera [72, 73] and a swept laser source-based system that uses a single detector [74–78]. Fourier-domain phase-resolved Doppler OCT combines Fourier-domain OCT with the phase-resolved method and has the advantage of high-sensitivity, fast imaging speed, and large velocity dynamic range [35–39].
A schematic diagram of a swept source-based Fourier-domain Doppler OCT system is shown in Fig. 41.3. The output light from the swept light source is split into reference and sample arms by a 1 × 2 coupler. Two circulators were used in both reference and sample arms to redirect the back-reflected light to a 2 × 2 fiber coupler (50/50 split ratio) for balanced detection. In the reference arm, an EO phase modulator was used to generate a stable carrier frequency for elimination of the Fourier transform generated mirror image and low frequency autocorrelation noise [76].
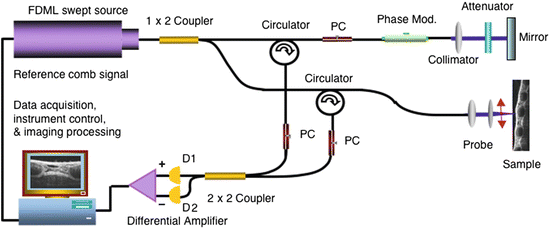

Fig. 41.3
Schematic of a swept source-based Fourier-domain Doppler OCT system
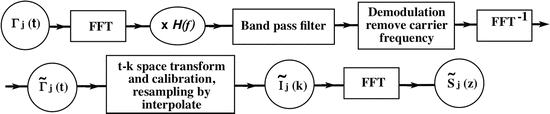
The complex analytical depth-encoded signal was converted from the detected time fringe signal by the digital approach shown in the following block diagram [38] (Fig. 41.4), where FFT denotes the fast Fourier transform, FFT−1 denotes the inverse fast Fourier transform, and H(f) is the Heaviside function given by
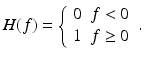
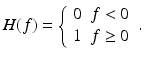
(41.23)

Fig. 41.4
Signal processing diagram for processing Doppler signals in swept source-based Fourier-domain Doppler OCT (From [38])
The time fringe signal Γ(t) acquired with wavelength scanning is firstly transformed from time to frequency space by FFT. Multiplication of H(f) selects the positive term of the Fourier transformed signal. The signal is then band-pass filtered to remove the low frequency and DC noises. The subsequent demodulation step shifts the center frequency of the filtered interference term from the carrier frequency to zero. The frequency fringe signal is then converted back to time space by inverse FFT. To cancel the distortion originating from nonlinearities in the wave number function k(t), the data are numerically remapped from uniform time to uniform wave number space based on the function of k(t), which is determined by the spectra calibration process provided by calibration comb signals generated from a fiber Fabry-Perot interferometer. Dispersion calibration is also performed at this step by adding a wave number-dependent phase term. The last FFT performed in k space retrieves the complex depth-encoded fringe signal 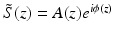 , which contains both the amplitude A(z) and phase ϕ(z) terms.
, which contains both the amplitude A(z) and phase ϕ(z) terms.
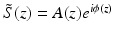 , which contains both the amplitude A(z) and phase ϕ(z) terms.
, which contains both the amplitude A(z) and phase ϕ(z) terms.Using the phase-resolved method, the Doppler frequency shift and Doppler variance can be determined from the depth-encoded complex fringe signal 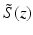 [38]:
[38]:
![$$ {f}_n=\frac{1}{2\pi T}\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}\left(\frac{\mathrm{Im}\ \left[{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N{\tilde{S}}_j\left({z}_m\right)\cdot {\tilde{S}}_{j+1}^{\ast}\left({z}_m\right)}\right]}{\mathrm{Re}\ \left[{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N{\tilde{S}}_j\left({z}_m\right)\cdot {\tilde{S}}_{j+1}^{*}\left({z}_m\right)}\right]}\right) $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ24.gif)
and
![$$ {\sigma}^2=\frac{1}{{\left(2\pi T\right)}^2}\left(1-\frac{\left|{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N{\tilde{S}}_j\left({z}_m\right)\cdot {\tilde{S}}_{j+1}^{*}\left({z}_m\right)}\right|}{\frac{1}{2}{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N\left[\kern0.1em {\tilde{S}}_j\left({z}_m\right)\cdot {\tilde{S}}_j^{*}\left({z}_m\right)+{\tilde{S}}_{j+1}\left({z}_m\right)\cdot {\tilde{S}}_{j+1}^{*}\left({z}_m\right)\right]}}\right). $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ25.gif)
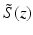 [38]:
[38]:![$$ {f}_n=\frac{1}{2\pi T}\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}\left(\frac{\mathrm{Im}\ \left[{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N{\tilde{S}}_j\left({z}_m\right)\cdot {\tilde{S}}_{j+1}^{\ast}\left({z}_m\right)}\right]}{\mathrm{Re}\ \left[{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N{\tilde{S}}_j\left({z}_m\right)\cdot {\tilde{S}}_{j+1}^{*}\left({z}_m\right)}\right]}\right) $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ24.gif)
(41.24)
![$$ {\sigma}^2=\frac{1}{{\left(2\pi T\right)}^2}\left(1-\frac{\left|{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N{\tilde{S}}_j\left({z}_m\right)\cdot {\tilde{S}}_{j+1}^{*}\left({z}_m\right)}\right|}{\frac{1}{2}{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N\left[\kern0.1em {\tilde{S}}_j\left({z}_m\right)\cdot {\tilde{S}}_j^{*}\left({z}_m\right)+{\tilde{S}}_{j+1}\left({z}_m\right)\cdot {\tilde{S}}_{j+1}^{*}\left({z}_m\right)\right]}}\right). $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ25.gif)
(41.25)
A spectrometer based Fourier-domain Doppler OCT is shown in Fig. 41.5 [37]. The signal from the Michelson interferometer is directly coupled to a spectrometer that records the spectral fringe pattern, P Doppler OCT (ν). The temporal interference fringe can be calculated by a Fourier transformation of the spectral fringe pattern (Eq. 41.17). The Doppler shift and variance can then be determined using phase-resolved Doppler OCT algorithms (Eqs. 41.21 and 41.22).
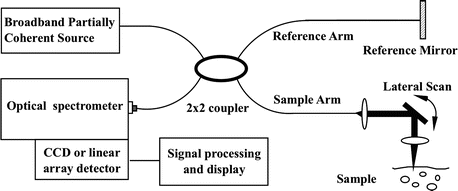

Fig. 41.5
Schematic of a spectrometer based Fourier-domain Doppler OCT system
Phase-resolved D-OCT using cross-correlation between A-lines decouple velocity sensitivity, spatial resolution, and imaging speed. The development of FD-OCT greatly increased imaging speed, which enables cross-correlation not only between sequential A-lines in B-scan but also sequential A-lines in C-scan (Fig. 41.6) [12, 79]. For sequential A-lines in B-scan, T is the inter-A-line time. For sequential A-lines in C-scan, T is the inter-frame time. Therefore, a large velocity dynamical range can be achieved since the T can be increased by several orders of magnitude, which makes it possible to image and quantify flow in the capillary level [79].
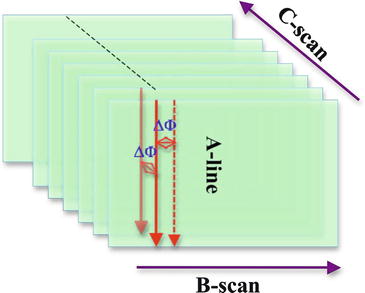

Fig. 41.6
Schematic signal processing diagram for the phase-resolved D-OCT system
Figure 41.7 shows the PR-D-OCT images of a flow phantom pumped at different speeds using a swept source-based FD-OCT system with an A-line rate of 50 kHz. Figure 41.7a–d are PR-D-OCT images of the flow phantom pumped at, respectively, 0.1 μl/min, 0.3 μl/min, 0.6 μl/min, and 1.1 μl/min. It should be noted that the phase is wrapped in Fig. 41.7c, d, which can be unwrapped [27]. The increase of Doppler frequency shift with the increase of pumping speed can be clearly seen from the PR-D-OCT images. Figure 41.7e shows the velocity profile along a horizontal cross section passing through the center of the tube in Fig. 41.7b.


Fig. 41.7
PR-D-OCT images of a flow phantom which is pumped at different speeds: (a) 0.1 μl/min, (b) 0.3 μl/min, (c) 0.6 μl/min, and (d) 1.1 μl/min. (e) Velocity profile along a horizontal cross section passing through the center of the tube in (b)
41.2.3 Doppler Variance, Transverse Flow Velocity, and Doppler Angle Determination
One of the limitations of using Doppler shift to determine the flow is that the technique is only sensitive to longitudinal flow velocity (Fig. 41.1). If one knows the flow direction, Doppler shift measurement can fully quantify the flow. However, in many biological cases where flow direction is not known, Doppler shift measurement alone is not enough to fully quantify the flow. Furthermore, there are many clinical cases, such as ocular blood flow, where vessels are in the plane perpendicular to the probe beam. When flow direction is perpendicular to the probe beam, the Doppler shift is not sensitive to transverse flow V T . Therefore, a method to measure transverse flow velocity is essential.
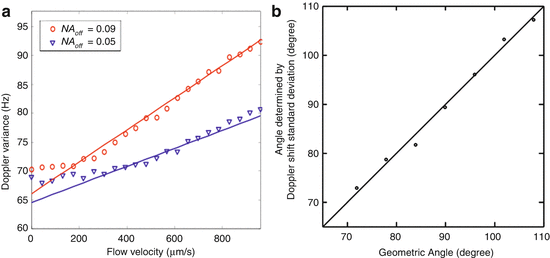
Doppler variance can be used to determine the transverse flow. The technique is based on the fact that Doppler OCT imaging uses a relatively large numeric aperture lens in the sample arm. The beam from different sides of the edges will produce different Doppler shifts, f 1 and f 2 , as indicated in Fig. 41.8. Consequently, the Doppler spectra will be broadened by the transverse flow. If the incident beam has a Gaussian spectral profile and contributions from Brownian motion and other sources that are independent of the macroscopic flow velocity are included, a linear relation between standard deviation of the Doppler spectra and transverse flow velocity, V T = Vsinθ, can be written as [13]
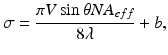
where b is a constant and NA eff is the effective numeric aperture.
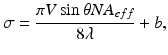
(41.26)

Fig. 41.8
Effect of numerical aperture and transverse flow velocity on Doppler bandwidth
The Doppler variance can be determined from the measured analytical fringe signal using Eq. 41.22. We have measured the σ value as a function of the transverse flow velocity (Fig. 41.9a) [13]. As predicted, the Doppler bandwidth is a linear function of transverse flow velocity above a certain threshold level. The effective numerical aperture of the optical objective in the sample arm determines the slope of this dependence. This result indicates that standard deviation can be used to determine the transverse flow velocity. Since both longitudinal and transverse flow velocities (V L and V T ) can be measured by the Doppler shift and standard deviation, respectively, flow direction can be determined from a single measurement of the Doppler fringe signal [80–82]. Figure 41.9b shows the comparison of angle determined by phase-resolved Doppler OCT and the geometric angle [82].
We have demonstrated that an arbitrary velocity vector can be determined from a single measurement by generating multiple Δk vectors with different pathlength delays simultaneously [83]. A beam divider which has three parts with different thicknesses of 0, t, and 2 t was inserted in the sample arm as shown in Fig. 41.10a. After passing through the focusing lens, the divider produced five independent Δks and divided a probe beam to have five independent view points and path length delays (Fig. 41.10b). Figure 41.10c shows Doppler images of a scattering fluid flowing through a microtube from a single scan. The five Doppler images correspond to five different Δk with different pathlengths. The velocity vector field can be quantified by solving a three-dimensional minimization problem from five Doppler images. The results are shown in Fig. 41.10d and have good agreement with the actual values [83].
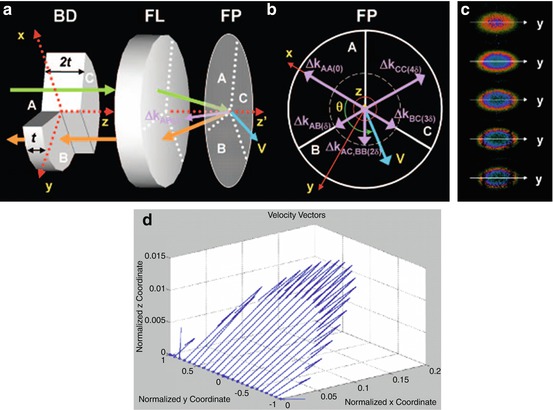

Fig. 41.10
The beam divider (a) that generates five independent Δk with different pathlength delays (b). Velocity vector field measured by the multi-angle Doppler OCT along the diameter of the microtube. Velocity vectors shown in (d) were determined from the five Doppler images in (c) (From [83])
In addition to the phase-resolved Doppler variance (PR-DV) method, methods that are dependent on the intensity or amplitude fluctuation can also be used for mapping vascular networks [43, 45, 46, 51, 84]. Recently, we have developed an intensity-based Doppler variance (IB-DV) method that uses an algorithm derived from a modified phase-resolved Doppler variance algorithm [43]:
![$$ {\sigma_{IB}}^2=\frac{1}{{\left(2\pi T\right)}^2}\left(1-\frac{{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N\left|{\tilde{S}}_j\left({z}_m\right)\cdot {\tilde{S}}_{j+1}^{\ast}\left({z}_m\right)\right|}}{\frac{1}{2}{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N\left[{\tilde{S}}_j\left({z}_m\right)\cdot {\tilde{S}}_j^{\ast}\left({z}_m\right)+{\tilde{S}}_{j+1}\left({z}_m\right)\cdot {\tilde{S}}_{j+1}^{\ast}\left({z}_m\right)\right]}}\right). $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ27.gif)
![$$ {\sigma_{IB}}^2=\frac{1}{{\left(2\pi T\right)}^2}\left(1-\frac{{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N\left|{\tilde{S}}_j\left({z}_m\right)\cdot {\tilde{S}}_{j+1}^{\ast}\left({z}_m\right)\right|}}{\frac{1}{2}{\displaystyle \sum_{m=\left(n-1\right)M}^{nM}}\ {\displaystyle \sum_{j=1}^N\left[{\tilde{S}}_j\left({z}_m\right)\cdot {\tilde{S}}_j^{\ast}\left({z}_m\right)+{\tilde{S}}_{j+1}\left({z}_m\right)\cdot {\tilde{S}}_{j+1}^{\ast}\left({z}_m\right)\right]}}\right). $$](/wp-content/uploads/2017/03/A76297_2_En_42_Chapter_Equ27.gif)
(41.27)
41.2.4 Qualitative and Quantitative Microvascular Imaging and Optical Microangiogram
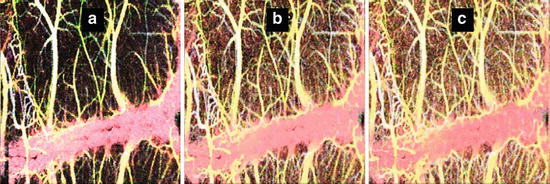
PR-D-OCT and Doppler variance (DV) imaging provide complementary information. While PR-D-OCT is most sensitive when the flow direction is along the probing beam, PR-DV and IB-DV can be used to measure the flow when the flow direction is near perpendicular to the probing beam. The sensitivity and dynamic range of these methods are limited by the time interval T between A-lines [79]. Figure 41.11 shows measured PR-DV and IB-DV values as a function of transverse flow speed [79]. At low speed regions up to 100 mm/s, the curve shows a linear relationship between the flow speed and the variance values. At higher flow speed regions, the curve shows saturation of the variance value.
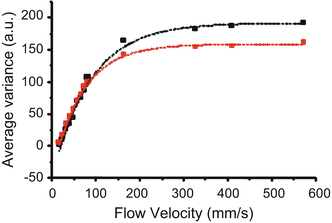

Fig. 41.11
The dependence of IB-DV and PR-DV values on the flow rate with a 50 kHz swept source-based FD-OCT (From [79])
There are many applications where mapping of microvascular network is essential for diagnosis and management of diseases that have a vascular etiology. Although PR-D-OCT provides high-sensitivity measurement of flow velocity, the technology is very sensitive to phase stability of the OCT system, the motion artifact, and orientation of the vasculature. In applications where absolute flow velocity is less important than vessel distribution, Doppler variance has the advantage of being less sensitive to the pulsatile nature of the blood flow and the complex variation of incident angle and provides an excellent method for optical angiogram [22, 27, 28, 40–43]. Figure 41.12 shows cerebrovascular circulations in mice obtained by a swept source OCT system. PR-D-OCT, PR-DV, and IB-DV images are shown in Fig. 41.12a–c, respectively. Both of the variance methods are able to detect the capillary vessels with high sensitivity and high contrast. PR-D-OCT is also sensitive for capillary vessel detection. However, the contrast of the PR-DV and IB-DV images is better than that of an PR-D-OCT image, especially in regions with smaller blood vessels.