Tonometry, Tonography, and Aqueous Fluorophotometry
Pratap Challa
Leon W. Herndon
David K. Dueker
Tonometry
Determination of the intraocular pressure (IOP) is a central feature in the diagnosis and management of the glaucomas. A true measurement of IOP requires a direct fluid connection to the anterior chamber. Cannulation of the anterior chamber for measurement of IOP is used frequently in the laboratory and occasionally during surgery. This approach entails too many hazards for the routine clinical management of glaucoma, however. Therefore, we generally use indirect measurements of IOP—tonometry.
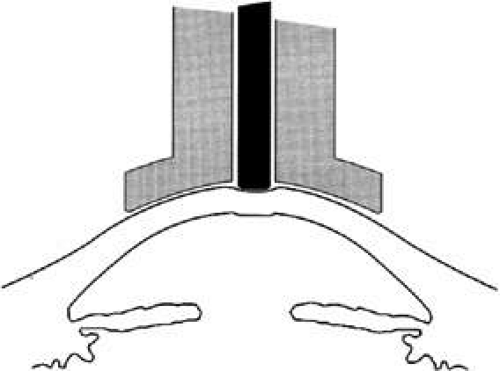
The pressure inside a flexible sphere can be estimated by using fixed forces to create measurable deformations of the wall or, conversely, by using variable forces to produce predetermined deformations of the sphere wall. Both approaches have been used in tonometry of the eye. The methods used are based on the Imbert-Fick principle, which states that if a plane surface is applied to a spherical membrane to cause a flattening of surface area, the pressure inside the spherical membrane will be equal to the applied force divided by the area of contact (Fig. 1).1,2 It must be emphasized that the Imbert-Fick principle is considered valid when the sphere is perfectly round, dry, elastic, and infinitely thin. Because the wall of the eye is none of these, application of the Imbert-Fick principle to tonometry requires careful attention to variations caused by the fundamental nature of the ocular tissues and to careful calibration of all tonometers in the laboratory.
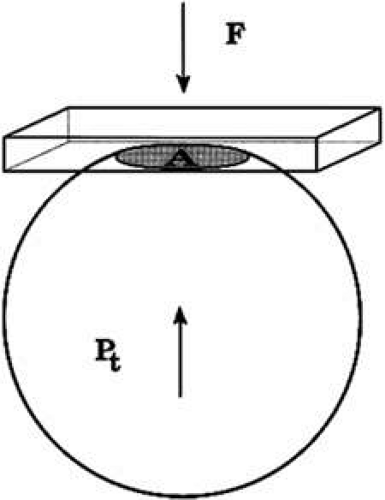 FIGURE 1. The Imbert-Fick principle. When a plane surface is applied to a flexible sphere with a force (F) causing an area (A) to be flattened, the pressure inside the sphere, Pt = F/A. |
During the years 1905 to 1926, Hjalmar August Schiøtz, a Norwegian ophthalmologist, produced and refined a mechanical indentation tonometer.3 This tonometer uses a weighted plunger that rides freely in the center of a hollow cylinder (Fig. 2). The outer cylinder has a footplate with a concave radius of 15-mm curvature, which rests on the cornea during measurement. The weighted plunger indents the cornea centrally, and the amount of indentation is transferred to a scale at the top of the instrument by a lever mechanism, which converts 0.05 mm of plunger movement into 1-mm units on the read-out scale. It is clear that a soft eye allows more plunger indentation than does a hard eye; the Schiøtz scale displays large amounts of indentation as high-scale readings and small amounts of indentation as low-scale readings.
It is necessary to use calibration tables to translate the readings made during tonometry into an estimate of the pressure that existed in the eye before the application of the tonometer. IOP during tonometry is called Pt, whereas IOP in the resting state before application of the tonometer is known as “P naught” or P0. One of the major contributions of Dr. Jonas Friedenwald was the calibration of the Schiøtz tonometer, which included a careful scientific study of the relation between Pt and P0.4,5
The indentation of the cornea caused by the Schiøtz tonometer displaces a small volume of fluid into the eye. This displaced fluid is accommodated by stretching or expansion of the ocular coats. Dr. Friedenwald found that the volume of fluid displaced was related to the logarithm of Pt by a factor that he called scleral rigidity. The tables that are commonly used to estimate IOP based on a Schiøtz scale reading assume an eye with normal scleral rigidity. It is important to remember that the tables give inaccurate estimates of IOP in eyes that do not have normal scleral rigidity.
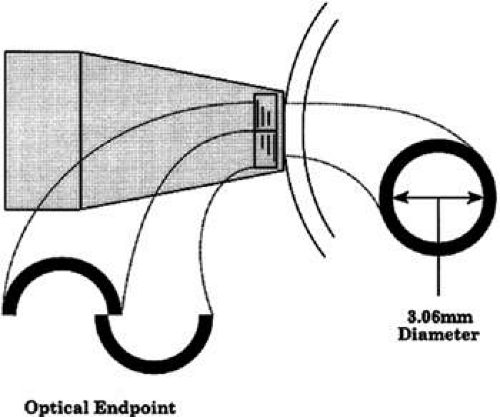
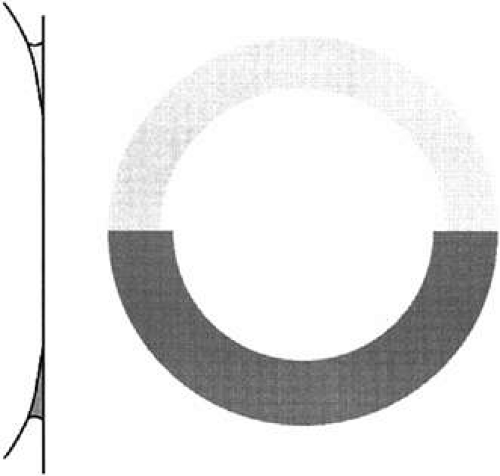
Using an applanation technique in which the cornea is flattened—not indented—eliminates many of the uncertainties of indentation tonometry. In the classic method developed by Goldmann, a circular area of the central cornea is flattened by pushing a plastic tonometer tip against the eye. The circle of applanation is delineated by a fluorescein-stained tear film (Figs. 3 and 4). The force required to flatten a circle of 3.06 mm is in grams a tenth of IOP in mmHg. Therefore, a force of 1.6 g is required to flatten this circular area when IOP is 16 mmHg. The 3.06-mm diameter circle of applanation was chosen because of this simple 10:1 relation between IOP and grams of force; this area is within the range in which the natural bending force of the cornea is canceled by the capillary attraction created by the tear film between the tonometer head and the cornea.6,7 Flattening so small an area of the cornea creates little fluid displacement within the eye. Therefore, scleral rigidity is not a major factor in Goldmann applanation tonometry.
Other tonometric instruments are available. It is a credit to the design and precision of the Goldmann instrument that virtually all new tonometers are evaluated in comparison with it. The air-puff tonometer (American Optical) works on an applanation principle in which the force required to flatten a portion of the cornea is delivered in a carefully calibrated bolus of air rather than through mechanical contact.8 The moment of flattening is recorded optoelectronically and converted into an estimate of IOP by a computer in the machine. This instrument may be useful when many patients need to be screened or it is desirable or necessary to avoid topical anesthesia.
When the cornea is scarred, irregular, or edematous, it is useful to have a tonometer available that does not depend on an optical end point for its measurement. Two instruments are useful in this instance: the Mackay-Marg tonometer9,10 and the Pneumotonometer.11 The Mackay-Marg tonometer has a central piston with provision to sense force surrounded by a passive annulus (Fig. 5). This instrument is brought up to the cornea by hand and the force necessary to applanate the cornea to the diameter of the central piston is determined by an electronic display.12 In the Pneumatonometer, a plunger is also brought up to the cornea by hand but the actual force of application is supplied by compressed gas. A valving mechanism at the tip of the plunger determines the end point for the measurement; the gas pressure necessary to achieve the end point is sensed and displayed electronically.13 Laboratory and clinical studies have shown that the Pneumatonometer causes some degree of indentation.14,15
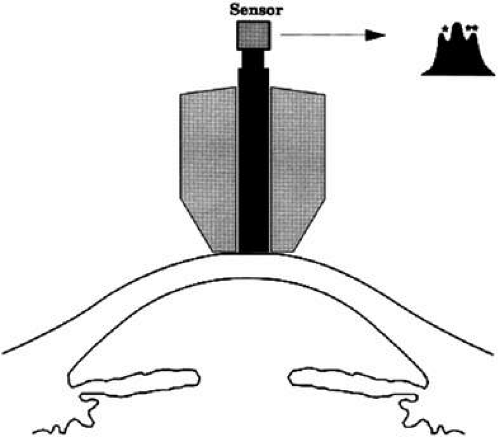
Dynamic contour tonometry (DCT) is a method of measuring transcorneal and continuous IOP where the pressure-sensitive tip is not planar, but instead, closely resembles the curvature of the cornea. A pressure sensor is embedded in the shell-shaped tonometer tip (Fig. 6). Forcing the central disc area of the cornea into the contour DCT tip allows the examiner to measure the pressure of the eye directly on the external surface of the cornea because, in the condition of matched contours, the pressure on both sides of the cornea are theoretically equal. The IOP recorded by DCT is defined as the mean diastolic IOP during the period the tonometer was in contact with the eye.
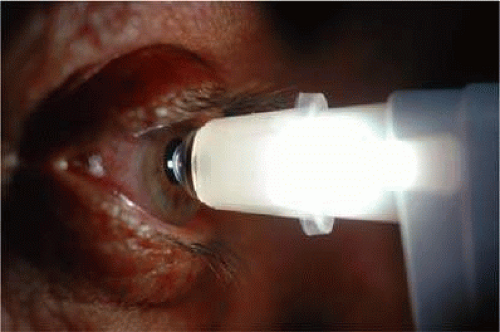 FIGURE 6. Demonstration of dynamic contour tonometry (DCT) measurement in a patient. The pressure sensitive tip closely resembles the curvature of the cornea. |
Investigation with the novel DCT on human cadaver eyes showed better absolute and relative accuracy than Goldmann and pneumatonometry.16,17 Instrument validation studies have shown that DCT is not significantly correlated with CCT.18,19 Kaufmann et al.20,21 and Siganos et al.22 reported that DCT seems to be less dependent on CCT than Goldmann tonometry or noncontact air-puff on normal eyes and on eyes after laser-assisted in situ keratomileusis, respectively.
The ocular response analyzer (ORA) determines corneal biomechanical properties using an applied force-displacement relationship. An air jet similar to that used in traditional air-puff tonometers generates force/pressure on the cornea (Fig. 7). To distinguish between corneal biomechanical properties and IOP, the ORA uses a method that eliminates the potential interference between the two factors in a single measurement. Pairs of measurements are used because a measurement of a single parameter cannot determine the independent corneal properties and IOP. This bidirectional applanation process provides a new measure of corneal biomechanics called corneal hysteresis. Recent articles have highlighted the clinical utility of the ORA and its various measurements.23,24,25
Normal Pressure
In the normal young adult population, the mean of IOP readings lies between 15 and 16 mmHg, with a distribution that is bell-shaped and symmetric (Fig. 8)26 With increasing age, most studies indicate a tendency toward increased IOP with skewing of the distribution toward higher pressures.27 Conversely, IOP in normal infants and children tends to run lower than that of the young adult population.28
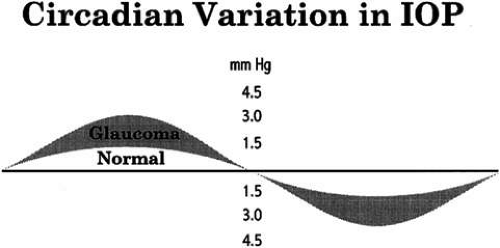
Circadian Variation in Intraocular Pressure
Intraocular pressure shows a natural cycle with a phase of relative elevation followed by a phase of relative depression occurring over a 24-hour period—a circadian rhythm.29 The mechanism for this variation almost certainly involves variations in aqueous humor production, although other factors contribute also. The magnitude of the variation is greater in glaucoma patients—in some studies, three or four times greater than in the normal population (Fig. 9). The larger pressure swing in glaucoma patients is logically related to poor outflow facility but because outflow facility and diurnal variation of IOP are not highly correlated, other factors also must play a role.
The most common daily cycle shows a tendency for higher pressures in the morning hours and falling pressures in the evening. This pattern is not universal, however, because peak pressures occur at any time of the day. Careful studies of IOP using home tonometry30 to track patients’ normal daily patterns have shown that about 50% of peak pressures fall outside normal office hours.31 Twenty-four-hour IOP monitoring studies also show a high incidence of peak IOPs outside normal office hours.32,33 The practical consequences of circadian variation in IOP are several.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree