Spectacle Lens Design
Gregory L. Stephens
Darryl J. Meister
The results of a refraction specify the power of a lens only at its center, or along its optical axis. As a patient moves his or her eyes to look away from the lens center, at an angle to the optic axis, undesirable optical effects (lens aberrations) occur that limit “off-axis” optical quality and decrease the field of clear vision. Lens aberrations represent the failure of the lens to produce a sharp focus at the desired focal position. It is the job of the spectacle lens designer to provide a lens with good off-axis optical quality by minimizing off-axis aberrations. The lens designer must also deal with optical and mechanical factors that are not associated with off-axis image quality. These include minimizing lens thickness, designing for unusual lens and frame shapes, maintaining eyelash clearance, and minimizing spectacle magnification differences.
Lens aberrations in an optical system can be controlled in many ways, including manipulation of lens surface curves, thickness, refractive index, and aperture stop position, among others. Nevertheless, the only variable that can be changed when designing conventional (nonaspheric) single vision spectacle lenses is the form or “bend” of the lens; that is, the relationship between the front and back surface powers of the lens. While the sum of the front and back surface powers must remain approximately constant to provide a given back vertex power, manipulating the relationship between the front and back surface powers represents the most effective technique for modifying the aberrations of a spectacle lens. Further, because the form of the lens is ultimately dictated by the power of at least one surface for a given back vertex power, the basic goal of the lens design process is to choose a base curve or front surface power that provides the best off-axis optical quality for a given lens power. In practice, a single base curve is actually used for a small range of powers with other base curves used for other powers. This results in a base curve series, a set of base curve steps (e.g., +0.50 D, +2.00 D, +4.00 D, +6.00 D, +8.00 D, and +10.00 D) that will be used for all of the possible lens powers that might be prescribed. In general, the more base curves that are available for a given lens series, the broader the prescription range of the product. Manufacturers provide base curve selection charts that present the recommended prescription range for each base curve of a series. The optical laboratory makes the base curve choice from the semi-finished lens series used for multifocal lenses, usually based upon the recommendation from the manufacturer. The base curves of finished stock lenses are chosen by the manufacturer before the lenses are sold to the optical laboratory.
Improvements in lens manufacturing technology have resulted in the increased use of high-index lens materials and in the development of aspheric and atoric lens designs that can be used for essentially any lens power. Proper spectacle lens design has become more important than ever before.
Refractive Error, Visual Acuity, and Contrast
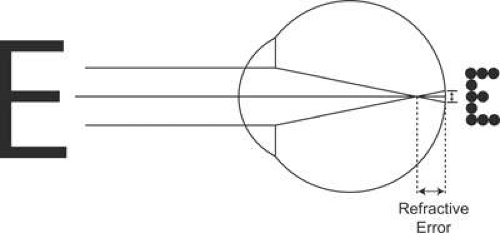
Ignoring the effects of diffraction, which become most significant at small pupil sizes, the in-focus retinal image of a point object is a point image. A large (extended) object consists of a large number of points, and a lens will form an image of each point on the object. When the image is out-of-focus, as occurs with an uncorrected refractive error, it will consist of a myriad of overlapping blur circles with each blur circle corresponding to an out-of-focus image of a single point on the object (Fig. 1). Blur circles must reach some threshold size before refractive error causes perceptible image blur. This threshold actually increases with object size, since a larger target can be resolved more easily than a smaller target in the presence of the same amount of blur. For a given object size, the range of refractive errors over which a patient cannot notice blur is known as the depth of focus.
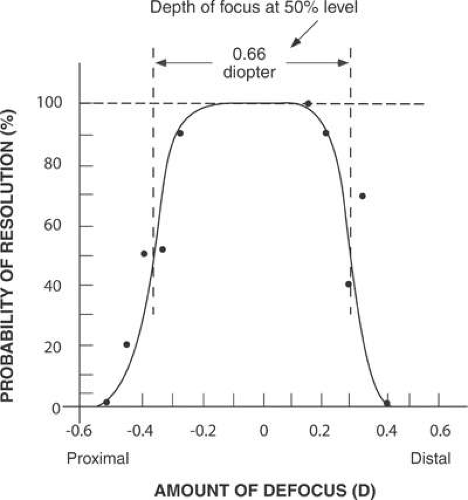
Clinical experience demonstrates that the threshold refractive error for perceiving blur varies widely from patient to patient. Some patients notice the smallest refractive error as a decrease in visual acuity or contrast, whereas others are happy with 2.00 or 3.00 diopters (D) of blur. In part, variations in visual acuity with refractive error can be attributed to the depth of focus. For average pupil sizes, a 20/25 (6/7.5) high-contrast target can be out of focus at least 0.20 D in either the myopic or hyperopic direction with no noticeable effect on target resolution (Fig. 2). A 50% probability of resolution is maintained to approximately 0.33 D of blur. For higher target luminances and smaller pupil sizes, depth of focus can be expected to be even larger. Depth of focus is greatly decreased under conditions of low luminance (large pupils) and reduced object contrast.1,2
Visual acuity variations may also be perceptual in origin. We sometimes think we “see” an object when we actually do not because we may function by recognition rather than by identification or visual acuity. For example, the letter A can often be recognized under conditions of poor visibility because it has the shape of a triangle. C, O, and Q may be more difficult to differentiate because of the similarities in shape. A street name may be recognized by its length. Thus, reading “acuity” is possible without resolution of the detail.
When in familiar territory under adverse conditions, we tend to navigate by recognition of landmarks rather than by reading signs or actually seeing low-contrast detail, such as a curb or a raised traffic island. However, where surroundings are not familiar or where unexpected objects may be in our path, good visual acuity becomes essential. If we are on an unfamiliar expressway, we must be able to read the signs. If we are approaching an unlit object, we must be able to resolve it from a dark background. Detecting a large object requires good differentiation of its edges, which is a critical visual acuity task.
Once the depth of focus is exceeded, a refractive error degrades visual acuity. Each 0.25 D step of myopic refractive error (outside the depth of focus) decreases visual acuity by approximately one line on a Snellen chart,3,4 up to about 20/100 visual acuity, when chart step sizes become large. Hyperopic errors have much less effect because accommodation can compensate for the error. The effect of an astigmatic refractive error is approximately 80% of a myopic error of the same magnitude,3,4 and the axis of the cylinder may also affect visual acuity, especially letter recognition. The off-axis aberrations of a spectacle lens create power errors that have the same effects on visual acuity as spherical or astigmatic refractive errors.
The importance of small refractive errors and the need for precise refractive correction were emphasized by Allen,5 who measured automobile braking distance when approaching an unlit vehicle in the presence of a glare source. Available braking distance was reduced by 1 foot for each 0.01 D of myopic refractive error (100 feet/D).
Low light levels and poor contrast also decrease visual acuity, and the effects are much worse for older patients (Fig. 3). Only young patients can achieve 20/20 (6/6) visual acuity at low light levels. At the highest (best) acuity levels, the average 60-year-old person needs 10 times more light or two to three times more contrast than the average 20-year-old to see the same objects.6,7,8 Even young people need at least 30% contrast to resolve 20/20 objects. Older people need at least 40% contrast to see 20/30 (6/9) targets.7
Thus, proper lens design and precise refraction are particularly important when luminance and contrast are low and where resolution of objects rather than recognition is necessary. Some of the most challenging visual situations occur during night driving or in bad weather because of the prevailing low luminance and low contrast. Driving while facing a low sun and reading backlit signs or identifying roadside detail is also difficult. The writing on a chalky blackboard can be a low-contrast, low-luminance situation, as can some sports activities. Permitting a preventable refractive error or allowing off-axis lens aberrations further lowers the contrast of a patient’s visual world and makes these situations even more difficult.
Maximizing contrast requires a precise refraction and proper choice of lens parameters, especially base curve. Most patients are sensitive to 0.25 D changes in lens power, and some can differentiate 0.13 (1/8) D changes. The American National Standards Institute (ANSI) Z80.1-2005 dress ophthalmic lens standard recommends a tolerance of 0.13 D in the manufacture of most prescriptions,9 so errors of up to 0.13 D are not uncommon at the center of a lens. Even with optimal design, off-axis aberrations will still be present, particularly for prescriptions with cylinder power. The ophthalmologist or optometrist can minimize errors by fine-tuning the refraction to the nearest 0.25 D, and, if necessary, to the nearest 0.13 D. The last judgmental step should be in the minus power direction to allow the patient to use accommodation to compensate for any residual error. A low-contrast visual acuity test target, which increases the sensitivity to refractive errors, may allow a prescription to be fine-tuned for difficult seeing situations.
Night myopia may contribute to night-driving problems. At low light levels, the accommodative state of the eye can go to a “rest position,” focusing the eye for some intermediate distance other than infinity and making the eye effectively myopic.10 However, signs and lights often provide sufficient accommodative stimulus so that night myopia is not a problem. To prescribe for suspected night myopia, it may be necessary to provide the patient with trial lenses. The patient should be a passenger in a car driven at night and should test the appropriateness of the trial lenses before a prescription is finalized.
The Basis of Lens Design
The Far-Point Sphere
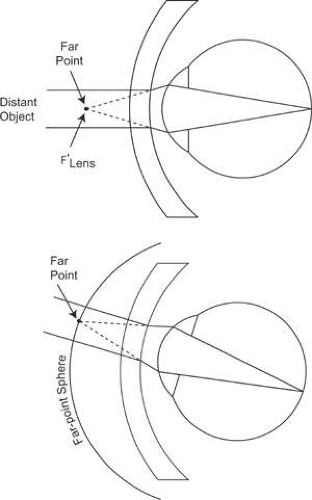
A patient’s refractive error is corrected when the image of a distant object as formed by the correcting lens falls at the patient’s far point. As the patient rotates his or her eye to use various portions of the lens, the far point also moves, tracing out a surface known as the far-point sphere (Fig. 4). The goal of the lens design process is to cause images of off-axis objects to fall on the far-point sphere. To accomplish this goal, off-axis lens aberrations must be reduced to minimal levels.
Lens Aberrations
Object-image relationships for a lens are usually based upon “first-order theory” or “Gaussian” optics, which assumes that the angles of incidence and refraction at a lens surface are small and near the optic axis; that is, within the paraxial region of the lens.11 Within this region the sine of an angle is nearly equal to the angle itself (expressed in radians), so the higher-order terms of a power series approximation of the sine of the angle can be ignored above the first-order (x1) term. Optical calculations based upon this assumption are considerably simplified, although they imply that all rays of light from a given object point will meet at one point to form the image. Such an optical system is ostensibly free of lens aberrations, although any magnification or minification remains present. At larger angles from the optic axis of the lens, however, the first-order paraxial approximations break down, and additional higher-order terms are required to predict with accuracy the refraction of light. When the next, third-order (x3) term is included in the power series for the approximation of the sine of an angle, the presence of lens aberrations is revealed. Lens aberrations that are independent of the wavelength or color of light (monochromatic aberrations) have been termed the Seidel aberrations, after Ludwig von Seidel, who described them mathematically in a series of papers in the 1850s.12 Two other aberrations exist that are related to the chromatic dispersion of a lens material, and these are the chromatic aberrations.
Monochromatic Aberrations
Of the five monochromatic lens aberrations, three – radial (or oblique) astigmatism, power error or curvature of field, and distortion – significantly degrade vision through off-axis areas of a spectacle lens. The magnification effects of lenses and the difference between the magnifications of the two lenses will also influence a patient’s vision and must be considered. The other two monochromatic aberrations, spherical aberration and coma, are the result of variations in power across an aperture. These two aberrations are generally negligible in moderate power single vision lenses because the pupil of the eye is relatively small, blocking the aberrated rays. Coma may be of importance in the design of progressive addition lenses.13
When a patient turns his or her eye to look at a point object that is not along the optic axis of a spectacle lens, the image of the point as formed by the lens may no longer be a point. Instead, the point may be imaged as two lines perpendicular to each other with one line closer than the other to the lens (Fig. 5). This aberration of the image is radial astigmatism. Radial astigmatism occurs because the refractive power through the tangential (or radial) meridian of the lens varies more rapidly away from the optic axis than the power through the sagittal (or circumferential) meridian perpendicular to it. This causes a difference in focal power between the two meridians at oblique angles of gaze. The effects of radial astigmatism on image formation are similar to those of astigmatism in general. If one of the line images falls on the far-point sphere, the patient sees the image of the point as a line. If the two foci straddle the far-point sphere, no sharp image is formed. Instead, the image is round and blurry (a blur circle). At other positions of the line images relative to the far-point sphere, the image formed is blurry and elliptical in shape. The separation of the two line foci formed by astigmatism is termed the Interval of Sturm, and the out-of-focus circular image formed between the two line foci is known as the circle of least confusion.14
If an off-axis extended object is viewed through a lens that has radial astigmatism, each point on the object is imaged as two line foci at different distances from the lens. For the example of Figure 6, each point on the vertical arms of the cross-object is imaged as a short horizontal line at the focus closer to the lens. Each point on the horizontal arms is also imaged as a large number of short horizontal lines, but the line images overlap along the length of the arms. If this image were to be formed at the far-point sphere of a patient’s eye, the patient would see the horizontal arms of the cross in sharp focus, while the vertical arms would appear blurry. At the focus farther from the lens, the situation is reversed with the vertical cross arms in sharp focus and the horizontal arms blurry. At the circle of least confusion, all points on the cross are imaged as out-of-focus circles, and both arms of the cross appear equally blurry. The appearance of the image differs at different distances from the lens.
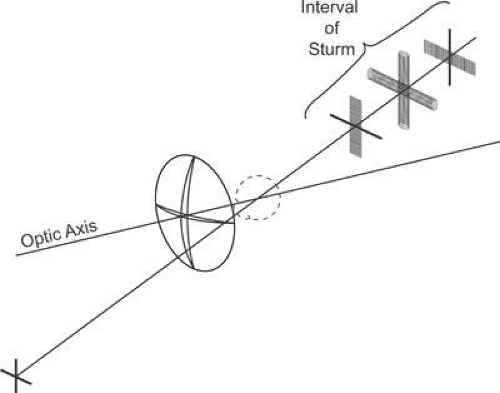 Figure 6. When an extended object is imaged through a lens that has radial astigmatism, the appearance of the image is different at different positions along the Interval of Sturm. |
A standard terminology describes the foci created by radial astigmatism. Suppose a patient were to look laterally (sideways) away from the center of a lens at a cross target. If the patient’s field of view is considered to be a circle on a vertical plane, with the cross pattern at the lateral edge of this circle, then the vertical arms of the cross are tangent to this circle. The focus of the vertical arms by the lens is termed the tangential focus, and errors in their focus position relative to the far-point sphere are tangential errors. Errors in focus that affect the cross arms perpendicular to the tangential detail (i.e., the horizontal cross-arms) are termed sagittal errors, and the focus of these lines is called the sagittal focus. If the patient were to look upward at a cross at the top of the field of view, the horizontal cross-arms would be tangential to the field-of-view circle, the focus of the horizontal cross-arms would be the tangential focus, and the image of the vertical cross-arms would form the sagittal focus. Tangential and sagittal focus errors increase as the distance from the center of a lens increases.
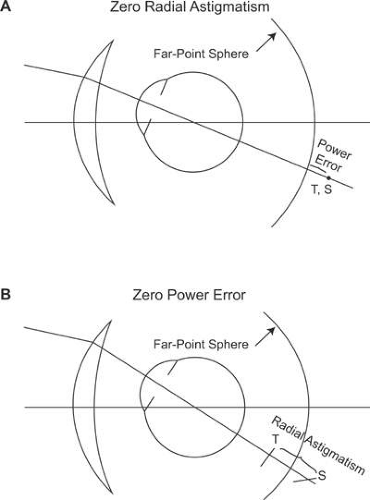
The amount of radial astigmatism present at a given point on a lens is defined as the dioptric difference between the two line foci, as measured from some reference surface. Changing the base curve of a lens alters the amount of radial astigmatism present, and there is usually an optimal base curve that results in zero radial astigmatism for a lens of given power.
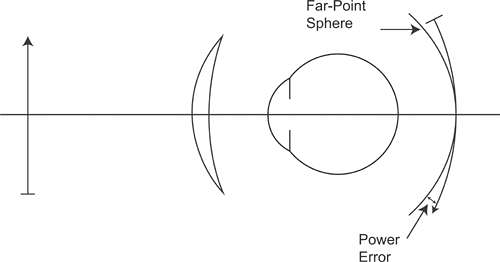
In the absence of radial astigmatism, the two focal lines formed by a lens collapse onto a single curved image surface known as Petzval’s surface. Curvature of field represents the error between a flat plane and Petzval’s surface. However, the ideal focusing plane of the eye, the far-point sphere, is also curved, and will not typically coincide with Petzval’s surface. This means that for most prescriptions some residual focusing error will remain, even when radial astigmatism has been eliminated. The error between Petzval’s surface and the far-point sphere is the power error of the lens for a given viewing angle. In the presence of radial astigmatism, power error represents the average error of the two focal lines formed by the lens from the far-point sphere. Consequently, power error is analogous to the spherical equivalent of the errors from the desired spectacle prescription (Fig. 7).
Because the tangential and sagittal astigmatic errors vary as a function of base curve, the average of these errors also varies. Therefore, power error, like radial astigmatism, changes with the base curve chosen for a lens, and there is usually an optimal base curve that will minimize or eliminate power error. This condition is satisfied when the tangential and sagittal errors are equal in magnitude but opposite in sign, resulting in an average error of zero. Consequently, with the exception of extremely high minus-power lenses in which both the sagittal and tangential errors can be completely eliminated at the same time, the base curve that eliminates power error is generally not equal to the base curve that eliminates radial astigmatism.15 When radial astigmatism is eliminated, there will be some residual power error, and when power error is eliminated, some uncorrected radial astigmatism will remain (Fig. 8). Choosing which aberration to eliminate completely is left to the discretion of the lens designer. In some cases, a lens design criterion may be chosen that represents a compromise, such as eliminating the tangential error, instead of eliminating either power error or radial astigmatism.
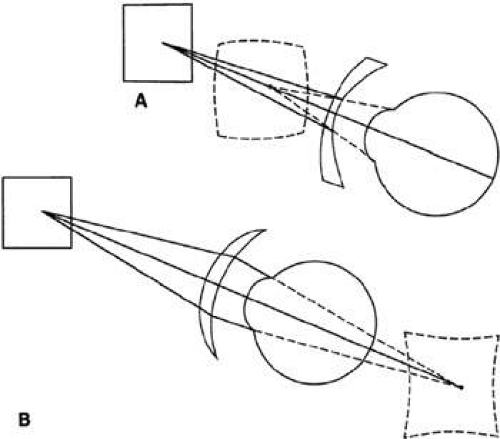
Distortion is a lens aberration caused by a variation in magnification from the center to the edge of a lens (Fig. 9). It has little effect on resolution of an image, but it does affect the image shape. When an extended object is imaged by a high minus-power lens that has decreasing magnification toward the lens periphery, the images of portions of the object farther from the lens center are magnified less than those closer to the center, resulting in a “barrel” distortion of the image. A plus-power spectacle lens, which has increasing magnification to the periphery, exhibits “pincushion” distortion. The effects of distortion are most noticeable in high plus-power (aphakic) spectacle lenses. Patients who wear these lenses often report that door frames and other rectangular or square objects appear bent. In addition, the combination of magnification and distortion in thick plus-power lenses results in a swimming sensation as the patient turns his or her head. These effects can be reduced in high plus-power lenses by using flatter aspheric designs.
Chromatic Aberrations
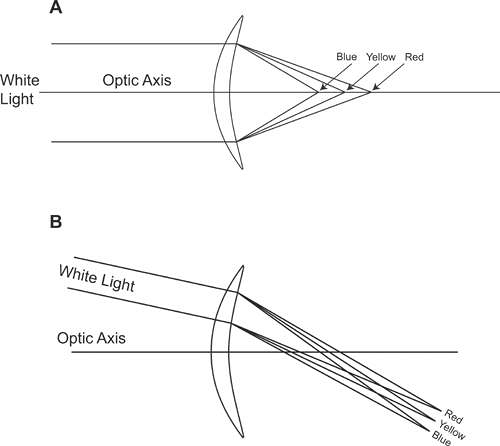
The various wavelengths that constitute visible light generally travel at different velocities through transparent media, which means that the refractive index of a lens material also varies as a function of wavelength or color. Short wavelength blue light, for instance, travels more slowly—and undergoes more refraction—through a lens material than longer wavelength red light, resulting in the phenomenon known as chromatic dispersion (Fig. 10), as is often seen through prisms. The degradation of image quality through an optical system that occurs as a result of dispersion is referred to as chromatic aberration, and two forms of chromatic aberration are typically recognized.
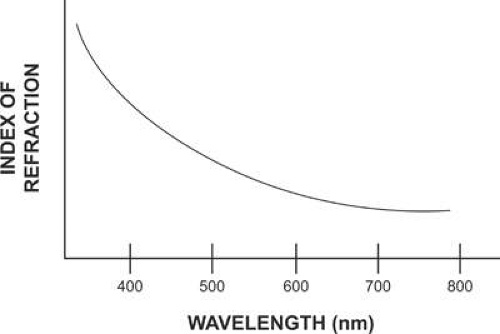 Figure 10. Dispersion is the variation of index of refraction with wavelength. It occurs in all lens materials and is responsible for chromatic aberration. |
Longitudinal chromatic aberration or axial chromatic aberration occurs along the optical axis of an optical system (Fig. 11A). Light rays of different wavelength passing through the lens focus at different distances from the lens because the index of refraction is different for each wavelength. In effect, the lens has a different power for every wavelength of light. Longitudinal chromatic aberration does not seem to have much effect on visual acuity under normal circumstances. This may in part be due to the depth of field of the eye. In addition, the red and blue wavelengths at the edges of the visible spectrum tend to be the most out-of-focus, but the eye is relatively insensitive to these wavelengths.16
Transverse chromatic aberration or lateral chromatic aberration, on the other hand, can have significant effects on off-axis vision. As a patient looks laterally to view a point object through a lens, the different wavelengths of light from the object are refracted at different angles, “smearing” the image into its component colors (Fig. 11B). Patients may describe this as blur or color fringes around objects. For an extended object such as a cross, the effects of transverse chromatic aberration will differ for different meridians. For example, when a patient looks laterally to view a cross object, each of the wavelengths of light from any point on the vertical arms of the cross is refracted horizontally at a slightly different angle, smearing the image of the vertical arms horizontally and resulting in color fringes that surround the image. The image of the horizontal cross-arms is relatively unaffected because the dispersion of light into its component colors occurs along the arms of the cross and is not noticeable except at the ends of the cross. Therefore, it can be argued that the effects of transverse chromatic aberration are more important for the tangential focus than for the sagittal focus. Transverse chromatic aberration is related to spectacle lens prismatic effects and is analogous to the dispersive effects visible when looking through a prism.
The prismatic effects of a lens vary with lens power and with the distance from the lens optical center that a light ray passes through the lens. The relationship is termed Prentice’s rule:17
where P is the amount of prism created, measured in prism diopters, h is the distance from the lens optical center, measured in centimeters, and F is the lens power in diopters. For example, the prism at a point 15 mm away from the optical center of a 4.00 D lens is 1.5 × 4.00, or 6 prism diopters. (The prism direction depends upon where the light ray passes through the lens and upon the sign of the lens power.) Prismatic effects are larger for higher-power lenses and larger angles of view, so transverse chromatic aberration, which is related to the prismatic effects of a lens, will be worse for these same conditions. High-index lens materials have more dispersion than CR-39 plastic or crown glass, so transverse chromatic aberration will also be more noticeable for high-index materials. Clinically, patients report color fringes or blur around objects only when looking away from the center of high-power, high-index spectacle lenses, and it is unusual for patients to report these problems unless their lens powers are greater than approximately ±5.00 D. The lens designer cannot vary the dispersion of a given lens material, so in a sense, nothing can be done about the visual effects caused by transverse chromatic aberration. However, proper lens design to minimize or eliminate other aberrations and proper fitting techniques in the optical dispensary can minimize total off-axis blur and improve off-axis visual acuity.
A Simple Demonstration
If one takes a large handheld magnifying glass and looks at a magazine with some vertical and horizontal lines or at a piece of graph paper, the effects of lens aberrations can be observed. With the glass held squarely with the paper and perpendicular to the line of sight, the field of view has good optical quality to the edge of the lens. If the lens is now tipped away at the top and the lines are viewed through the top of the lens, horizontal lines become blurred, colored and curved, whereas vertical lines are in better focus, straight, and uncolored. If the lens is tipped sideways, similar effects occur except that the vertical lines become more blurred. The blur is tangential error, the color is transverse chromatic aberration, and the curvature is distortion. The difference in blur between the horizontal and vertical lines is off-axis or radial astigmatism.
The Geometric Basis of Lens Design
Figure 12 shows the idealized geometric relationship of a spectacle lens to the eye. In the figure, the optic axis of the lens is shown as a dashed line that connects the centers of curvature of both lens surfaces and passes through the lens optical center. It is assumed when designing a lens that the optic axis also passes through the eye’s center of rotation. In spectacle lens design, the center of rotation is termed the optical stop of the system because its position determines which rays reach the fovea in off-axis gaze. The stop distance, or center of rotation distance, is the distance from the back surface of the lens to the center of rotation. Traditionally, this value has been assumed to be a constant, often 27 mm,18 but there is significant variation in this distance in the population. Lens designers calculate the optimal base curve for a lens based on this value. Throughout the history of spectacle lens design, the basic input that has linked the patient to the lens has been the center of rotation distance. The optical stop of the lens-eye system is where all the lines of sight to the various points in the field of view cross.
Let us assume that a spectacle lens is fitted at the same vertex distance as was used in the refractive examination or that the spectacle prescription has been compensated for any difference between the two. The image of a distant object then falls at the far point. As the eye rotates to look off-axis, the far point also rotates, tracing out the far-point sphere. Note that the center of the bundle of rays from the object passes through the center of rotation of the eye. By convention, the dioptric position of the focus of light is calculated relative to the reference sphere, the sphere tangent to the back vertex of the lens – or the location of the optical center at the back surface – and centered on the center of rotation of the eye. Errors in image formation from the far-point sphere can then be expressed as dioptric differences from the desired spectacle prescription or desired back vertex power.
Pantoscopic Tilt and Its Effects
Figure 13 illustrates the positioning of a frame and lens on the face. Most lenses are worn with the bottom tipped slightly toward the eye through an angle of about 6 to 10 degrees. This is the pantoscopic angle, and the frame is said to have pantoscopic tilt. A plane connecting the top and bottom of the orbit (the eyebrows and cheekbone) has some slight tilt from a vertical plane, so a slight amount of pantoscopic tilt is cosmetically attractive and maximizes field of view through a lens. Most frames, especially plastic frames, fit the nose such that the center of the lens is a few millimeters below the pupil when the patient is looking straight ahead. Fortunately, the combination of downward tip and lowered fitting position tends to keep the optic axis of the lens close to the center of rotation of the eye (within a few millimeters), and the lens back surface is automatically approximately on the reference sphere. In short, Figure 13 is Figure 12 tipped downward with some flexibility added.
The fit of a frame can be evaluated by drawing an imaginary line perpendicular to the eyewire at its vertical center and projecting backward into the eyeball, as shown by the solid line in Figure 13. The edge of a ruler placed against the frame and cheek area aids in visualization of the line. This line indicates the location of the optic axis of the lens. It should seem to pass approximately through the center of rotation. This point is behind the canthus, as shown in the figure.
Because the greatest use of lenses is for straight-ahead and downward viewing, the normal cosmetically attractive pantoscopic angle is also functionally desirable. For most prescriptions, departures from the ideal alignment shown in Figures 12 and 13 do not cause serious errors. However, when fitting high-power lenses (lenses for extremely high hyperopes and myopes, aphakic lenses), aspheric lenses, atoric lenses, and high-index lenses of relatively high power, pantoscopic tilt can create some problems. One, pantoscopic tilt alters the effective power through which the patient is looking when looking straight-ahead.19 As an example, adding pantoscopic tilt to a minus power lens increases the effective minus power of the lens and also adds plus-cylinder power at an axis of 90 degrees or minus-cylinder power axis 180 degrees. (Some undercorrected myopes may report this effect, stating that their vision is better when they tilt their glasses.) The power change is proportional to the lens power, so a patient’s vision can be blurred by the effects of pantoscopic tilt when lens power is high. Formulas that describe the effective power change caused by the tilt of a spherical power lens were described by Martin,19 and more general formulas that calculate the power change for any lens power are also available.20,21 It is possible to prescribe a lens power that compensates a patient’s spectacles for the effects of pantoscopic tilt, but this is not commonly done, at least for single vision lenses. Two, pantoscopic tilt alters the off-axis optical performance of a lens. When the pantoscopic tilt of a frame is such that the optic axis of a lens does not pass through the center of rotation of the eye, the fitting geometry used by the lens designer is no longer correct, and off-axis monochromatic aberrations will increase.22 Aspheric lenses are more sensitive to this effect than are standard spherical lens designs.23 High-index lenses have off-axis optical quality problems because of transverse chromatic aberration, and increases in monochromatic aberrations will only make the off-axis optical quality of these lenses worse.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree