Optics of Intraocular Lenses
Robert J. Schechter
The use of intraocular lenses (IOLs) has become the standard of care for cataract surgery, except for certain medical, economic, or social limitations. As surgical techniques have become more sophisticated and safe, and IOL manufacturing procedures have become more refined, the safety and desirability of IOLs have become indisputable. It is certainly one of the most dramatic improvements in ophthalmic rehabilitation in the history of medicine.
History of Intraocular Lenses
The first suggestion that an artificial lens might be inserted into an eye following cataract extraction was made in the 18th century by Casanova, who is perhaps better remembered for other contributions to medical and biologic technique.1 In 1949, the first IOL was inserted into a human eye by Harold Ridley in London.2 In 2000, he was knighted by Queen Elizabeth II for his contributions to medical science.
Ridley stated that “extraction alone is but half the cure for cataract.”3 Before IOLs (and contact lenses), such patients had to use aphakic (high plus) spectacle lenses. These aphakic lenses increase the image size 20% to 35% and have some disadvantages.4 The image magnification results in spatial disorientation and causes a newly aphakic patient to underestimate distances because magnified objects are judged to be closer. There are peripheral distortions of the visual fields and the so-called jack-in-the-box roving ring scotoma.
Optics
Image Magnification of Correcting Lenses
Most of the disadvantages of aphakic spectacle lenses are eliminated with the use of correcting aphakic contact lenses. Contact lens image magnification is in the range of 7% to 12%.4,5 IOLs result in an image magnification of 3% to 4%.4 Thus, as the lens correcting aphakia is brought closer to the original site of the crystalline lens, the image magnification decreases.
Image magnification is proportional to the angle at which light enters the eye.6 Figure 1 depicts an eye seeing an object at distance (“optic infinity”), with and without a correcting optic lens in place. The lens is a converging lens of focal length f: The distance between the correcting lens and the “entrance pupil” of the eye is denoted by d. (The site of the entrance pupil should be used in such analyses, because nodal point construction is theoretically incorrect in cases of the blurred imagery of the uncorrected eye.7)
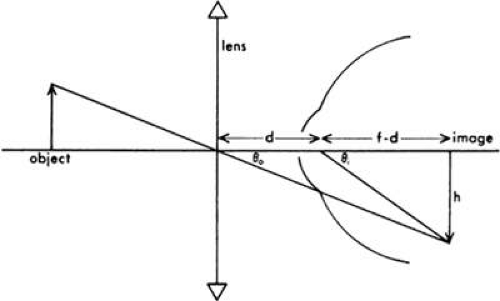 Figure 1. Image magnification induced by a correcting optical device of focal length fat distance d from the entrance pupil of the eye. |
With the lens in position, the eye sees the image of height h, formed at the focal length of the lens. Thus, the image is formed at distance f from the lens and enters the entrance pupil at angle θi. Without the lens in position, the “image” is the object itself, located at optic infinity. Because all light rays from a point on an object at infinity are parallel, the angular characteristics of any ray can be examined. Consider the light ray extending from the top of the object through the optic center of the lens. This ray passes through the top of the image as well, because light passing through the optic center of a lens is undeviated. This light ray from the object intersects the horizontal at an angle of θo. (Because light rays from the top of the object are parallel, they all enter the eye at the same angle and, therefore, it is legitimate and appropriate to consider this angle θo.)
The image magnification induced by this lens is, therefore, the ratio of the angles θi/θo. For small angles, the approximation θ = tan θ is valid. If θi and θo are considered to be sufficiently small, then
However,
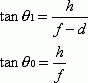
So,
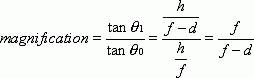
Because the power p of a converging lens is the reciprocal of the focal length,

It has further been shown that, given a contact lens of power Pc and a spectacle lens of power Ps correcting a given eye, the image magnification of the contact lens relative to that induced by the correcting spectacle is
Thus, as the distance of a convergent correcting optic device from the eye increases, so does the induced image magnification.6 An artificial lens placed in the posterior chamber would theoretically induce no image magnification. As the site of the IOL moves forward to the pupillary plane or the prepupillary space, the induced image magnification increases to the range of 3% to 4%.4,8
Optic Methods of Correcting Aphakia
Spectacle correlation of aphakia is associated with multiple optic disadvantages, as has been previously noted. Neither contact lenses nor IOLs have these disadvantages, and, so in that sense, both are optically superior methods of correcting aphakia. Both contact lenses and spectacles can be fitted to provide an essentially exact refractive correction of spherical and regular astigmatic errors. Patients can be evaluated after surgery, and the contact lenses or spectacles can be repeatedly modified as necessary. The power of an IOL, conversely, is determined before cataract extraction, and both the patient and the surgeon must accept the accuracy of the result.
Calculation of Intraocular Lens Power
With the advent of easy and accurate ultrasonic determination of the axial length of the globe, multiple methods of preoperative calculation of the necessary IOL power have been introduced, including computer programs and nomograms.9,10,11,12,13,14,15,16,17,18,19,20,21,22,23 The lens power can be calculated to result in emmetropia or iseikonia (with the necessary accompanying ametropia). Postoperative results have been reported with 1 diopter (D) of the preoperative calculation in 88% and 91% of eyes.19,20 Generally, excellent lens power predictions are found with various formulas.24,25
With a known value for anterior chamber depth (ACD), it is possible to calculate the desired power of the IOL.
a = axial length of the globe in meters
k = ACD
Pc = refractive power of the cornea
Pl = refractive power of the intraocular lens
n = index of refraction of the aqueous and vitreous
At the vertex of the cornea in such an eye, light must have a vergence of 1/a to cause the light to reach a focus in distance a, corresponding to the position of the retina. Similarly, at the papillary space, the required focal length is a – k. Because of the refractive index of the media, the reduced focal length of (a – k)/n must be used. Thus, the required vergence at the pupillary space is n/(a–k). The vergence contributed by the cornea must, however, be taken into consideration. A cornea of power Pc contributes, at the pupillary plane, a vergence of
Once again it is necessary to use a “reduced” distance of kÞshn owing to the index of refraction of the media.6
The vergence that remains to be supplied at the pupillary space is provided by the IOL.
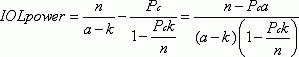
This formula was used to determine the IOL power of lenses that were inserted into 150 eyes.20 In 136 eyes, the postoperative refraction was within 1 D of the value calculated preoperatively; in 12 eyes, the refraction was within 1.1 to 2 D, and in only two eyes was the difference greater than 2 D. Thus, with the use of accurate methods (e.g., ultrasonography) to measure the axial length of the globe, estimates of the required IOL power can be made with some degree of accuracy.21,26,27,28 Hoffer29,30 has tabulated the accuracy of various formulas in predicting emmetropic IOL power.29,30
These so-called first-generation formulas assumed an ACD that was independent of the size of the eye. Various theoretically derived first-generation formulas for emmetropic IOL power have been examined graphically and algebraically.31,32,33 With the exception of Binkhorst’s formula, which predicts a value 0.5 D higher than the others, all the theoretically derived formulas are reducible to the same equation.4,31,32,33
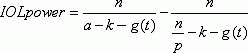
where g(t) is a function of lens thickness and is usually a small value. If lens thickness is not considered (“thin lens assumption”) and g(t) = 0, the previous equation reduces to the earlier derivation.
Regression Analysis
Intraocular Lens Formula
Sanders, Retzlaff, and Kraff Formula
Optic accuracy of IOL implantation depends on the accuracy of the formula used preoperatively to select the lens power. Several investigators have looked retrospectively at the results of larger numbers of IOL implantations in an attempt to approach the problem of predicting IOL power through an empiric approach.34,35,36 Their data were subjected to multiple regression analyses and mathematical curve-fitting techniques. They found that the power of an IOL could be best predicted by a formula of the form
where A, B, and C are constants for a given lens. Interestingly, no significant further accuracy was obtained by adding additional terms representing other factors, such as ACD. (One investigator substituted the actual measured postoperative ACD in the theoretic formula and only improved accuracy 3%.46 This tends to support the conclusion that ACD is only minimally important in IOL power calculation.)
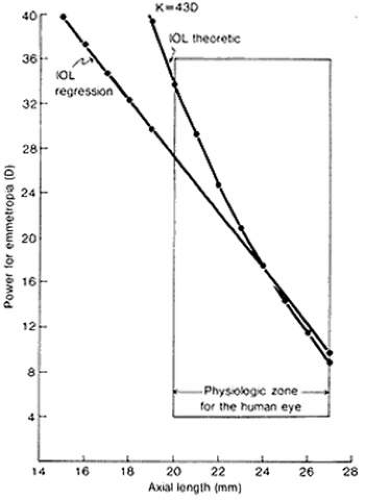
Any additional accuracy was also not obtained by inclusion of multiplicative terms (e.g., axial length × keratometry) to account for any possible interaction between variables, nor by inclusion of exponential terms (e.g., axial length squared) to account for any nonlinear characteristics in the mathematic model of lens power.34,35 These investigators concluded that the opticophysiologic relationship between IOL power, corneal curvature, and axial length is linear (or rather planar) and that, therefore, their empirically derived linear formula must be more accurate than the nonlinear theoretic formulas. They point out that many theoretic formulas, for example, tend to overestimate IOL power for axially short eyes, the area in which the theoretic and linear formulas tend to diverge most markedly (Fig. 2). Using a theoretically derived lens formula, Lindstrom38 has noted decreased accuracy with high or low axial length measurements. His calculated lens was too strong in the short eye and too weak in the long eye.38 Others have also noted this discrepancy between the two types of formulas for long or short eyes.39 Conversely, in one study of 40 myopic eyes that required an IOL of 13 D or less, both the theoretic and Sanders, Retzlaff, and Kraff (SRK) formulas were comparable.40
Sanders,35 and Retzlaff and Kraff36, in separate studies, further simplified the regression analysis-derived formula.35,36 The finding was a negligible loss of accuracy if the constants B and C in the original formula were universalized for all lenses and manufacturers. B, the coefficient of axial length, was calculated at -2.5, and C, the coefficient of the average keratometry in diopters, was determined to be -0.9. Thus, the power of any IOL may be determined by measuring the axial length and keratometry readings only and by knowing the particular A value for the lens in question. Thus, the simplified SRK formula is
This formula has been derived using the measured axial length, and no correction for retinal thickness is necessary. This formula is easier to use than the theoretically derived formulas and can even be calculated by hand with little difficulty. It requires neither a measurement nor an estimate of the preoperative or postoperative ACD or depth at which the lens is to be placed.
The SRK formula was said to be superior to the early theoretic formulas in having a smaller average error per case, a smaller range of error from the highest minus to the highest plus, and a smaller proportion of cases with greater than 2 D of error.34,35,36,41 Proponents of the theoretic formulas have countered that the difference between immersion versus contact methods of ultrasonography for determining the axial length may be a factor.
Contact methods of A-scan ultrasonography may indent the cornea and result in a falsely lowered axial length measurement.29,31,32,38 This may be one of the reasons for the increased error of the theoretically derived formulas’ predicting too-strong lenses for axially short eyes. Nevertheless, in a 1999 survey, immersion A-scan ultrasonography (compared with applanation ultrasonography) was still used by only 5% of responders.42 Another reason for this error in such eyes may be the assumption of a standard ACD for use in the theoretic formulas. Shorter eyes have shallower ACD.43,44 Use of a standard or average value for ACD in such cases may also contribute to the prediction of too-strong lenses, because the predicted power of the IOL increases with increasing ACD, all other factors remaining constant.
Second- and Third-Generation Intraoperative Lens Formulas
Although the so-called first generation IOL formulas were useful, they were less accurate for long or short eyes. These formulas assume a constant ACD (or position of the IOL) in all eyes, regardless of their axial length. Shorter eyes have shallower ACD.43,44 Use of a standard or average value for ACD in such cases contributes to the prediction of too-strong lenses, because the predicted power of the IOL increases with increasing ACD, all other factors remaining constant. The measured postoperative ACD was found to be directly proportional to the axial length of the eye; longer eyes had larger ACD. Several “second-generation” theoretic formulas emerged that replaced the constant ACD with one that included a correction for axial length.45
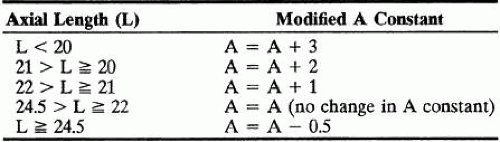
The SRK formula was also modified to improve accuracy for short and long eyes and reemerged as the SRK II formula. This was a simple modification of the original SRK.46 The only change was that the A constant is modified according to the axial length of the eye (Table 1).
Note in Figure 2 that this modification moves the SRK curve closer to the curve of the first-generation theoretic formula. To find the IOL power (1) required to produce a particular postoperative refraction R, I = P – (R × CR), where P is the predicted emmetropic IOL power and CR = 1.25 if P is greater than 14, CR = I otherwise.
Holladay et al.45 have noted that the axial-length versus calculated power graphs for second-generation formulas, both theoretic and regression derived, converge into the same general area.45 Although some have found the newer theoretic formulas to be superior to the SRK,47 another group compared the SRK II and four second-generation theoretic formulas.48 They found that the differences in predicted implant powers (in eyes of “normal” size) were smaller than differences caused by variations in axial length and keratometer measurements. In addition, significant differences exist in results obtained by different surgeons, thus supporting the idea of modifying the formulas for an individual surgeon, either by modifying the A constant49 or by use of a personalized “surgeon factor” in theoretic formulas.45
The originators of the SRK formula compared regression analysis-derived and theoretic formulas for calculating aphakic spectacle refraction.50 Unlike the situation with pseudophakic formulas, they found the two aphakic formulas approximately of equal accuracy. They believed, however, that the SRK-like formula was easier to use.
Thus, with second-generation formulas, ACD was no longer a constant in all eyes but rather varied with axial length. IOL power calculations continued to improve, however. Holladay et al.51 were the first to consider that the ACD might vary not only with the axial length but also with the corneal curvature.51 Their formula modified the ACD based on the axial length, and also based on the corneal height (distance from the cornea to the IOL’s first principal plane). This formula was shown to be significantly more accurate than previous theoretic formulas and the SRK II.52
Hoffer53 also developed a third-generation IOL formula.53 He speculated on the relationship between ACD and axial length and developed an expression that resulted in an S-shaped curve that fit his impression of what this relationship should be. This formula deepened the ACD with increasing axial length and deepened the ACD with increasing corneal curvature. This modification of ACD, tacked on to his previous Hoffer formula, has become known as the Hoffer Q formula.
The originators of the SRK formulas brought their retrospective analytic approach to third-generation IOL calculations.54 They hoped to combine the theoretic advantages of a physiologic optics approach (which might be more accurate in long or short eyes, out of the range of the database from which the SRK formulas had been developed) with the advantages of retrospective data analysis. They studied a third-generation theoretic approach to IOL calculation and tried to determine which values, correlations, and adjustments gave the most accurate result. They tried to consider all or most of the factors that had been used as modifications in various theoretic formulas. Their formula predicts postoperative ACD based on axial length. It includes a correction for long eyes. They developed a corneal height formula and an expression that predicted the white-to-white corneal width (which had not measured in their data.) They developed a retinal thickness correction to axial length. They studied what the optimal index of refraction was for IOL calculation. They showed how the SRK “A” constant could be correlated with the ACD value. The resulting formula was called the SRK/T (for theoretic) formula. As input, it requires only those same variables as earlier SRK formulas: the corneal curvature, axial length, and IOL A constant. They next compared the SRK/T with the SRK II, the Holladay, Binkhorst II, and Hoffer (note: this was not the Hoffer Q, which had not yet been developed). They found that all formulas had roughly the same accuracy, except for eyes of axial length exceeding 28.4 mm, in which the SRK II became significantly less accurate.
Hoffer55 compared the accuracy of three third-generation formulas: the Hoffer Q, the SRK/T, and the Holladay. He found all were superior to previous formulas, including the SRK II. No significant difference was seen among the three third-generation formulas, although there was a tendency for the Holladay formula (and in a later study, the SRK/T as well55) to be more accurate in eyes of 24.5 to 26 mm, the SRK/T in eyes of over 26 mm, and the Hoffer Q for eyes under 22 mm. For eyes in the range of 22 to 24.5 mm, Hoffer recommended using the average of all three formulas. One investigator compared formulas for microphthalmic eyes <19 mm long.56 He found the SRK/T to be best overall, although all predicted too weak a lens (and postoperative hyperopia). In a study of IOL in pediatric patients, the three third-generation formulas and the SRK II were compared.57 No difference among the four formulas was statistically significant.
To improve accuracy in short, hyperopic eyes, Holladay further modified his formula by including consideration of white-to-white corneal diameters, and anterior chamber and lens thickness measurements, as well as the patient’s age and preoperative refractive error. This Holladay 2 formula was introduced into clinical use in 1996; it has yet to be published, although it is available in some software packages. In one study, this Holladay 2 formula, and use of immersion A-scan measurements, resulted in improved accuracy for short eyes.58 Another retrospective analysis of 317 eyes was made and four formulas were compared: the Holladay 1, the Holladay 2, the Hoffer Q, and the SRK/T.55 This study found the Holladay 2 and Hoffer Q were (equivalent and) best in short eyes, the Holladay 1 and Hoffer Q were (equivalent and) best in average eyes, the Holladay 2 and SRK/T were (equivalent and) best in medium long eyes, with the SRK/T producing a trend toward better results in very long eyes. The Holladay 2 formula showed a “trend towards poorer performance in most axial lengths tested (89%).” Especially considering that the Holladay 2 formula requires the additional input of preoperative ACD, lens thickness, corneal diameter, patient’s age, and preoperative refraction, this investigator did not recommend its inclusion in the optimal IOL power calculation armamentarium.
The SRK II formula is certainly far easier to use than any of the third-generation formulas; calculations can be made quickly with pencil and paper. Conversely, however, third-generation formulas appear to be more accurate, especially in long and short eyes. Computing technology that calculates IOL power using these formulas is widely available in software packages, handheld devices, and even has been incorporated into many ultrasound A-scan units.
A nonformula approach has been described that might be useful with children or in other patients in whom accurate measurement might be difficult (those who had undergone previous refractive surgery, colobomas, and the like).59 Following lens removal, retinoscopy may be performed, or the patient may be moved and have a subjection refraction performed. The patient is then returned to the operating room for insertion of the IOL.
Factors Influencing Accuracy of Intraocular Lens Power Calculation
The accuracy with which IOL power can be calculated depends on several factors.
Measurement of Axial Length
Ultrasonography is the most widely used method to determine the axial length of the eye.21,27,28 Current ultrasonographic techniques permit an accuracy or reproducibility to within 0.1 mm or less in the axial length measurement.4
Binkhorst60 adds 0.25 mm to the measured axial length to compensate for the thickness of the retina in the area of the sound beam.60 Some studies have found increased accuracy with the addition of retinal thickness to the measured axial length.34 Others, however, have found their calculations more accurate when specifically not including any such retinal thickness correction factor.29,30,61 In a regression analysis of this question, retinal thickness corrections from 0 to 0.5 mm were tested and found to be approximately equivalent in accuracy.54 Noted, however, was that, in long eyes, smaller correction values were most accurate, whereas in shorter eyes, larger values were better. Optimal values ranged from 0.29 mm for an 18-mm eye to 0 mm for a 32-mm eye. One explanation for this finding is that it may result from the vagaries of ultrasound measurement; a shorter eye may have, in effect, a faster average speed of sound transmission because a higher percentage of its travel is in the crystalline lens. This would result in a falsely shorter measured axial length, for which the “retinal thickness factor” corrects.
An error of 0.1 mm in the axial length measurement will result in a postoperative refractive error of 0.25 D.4 Axial length measurements may differ, depending on the machine used to make the measurement.62
It is also possible that the axial length of the eye may change as a result of the surgical manipulations. This quantity is somewhat variable and unpredictable. One group of investigators found an average postoperative increase in axial length of 0.06 mm,18,27 whereas a second group reported an average decrease in axial length of the same amount. Hoffer43 found no significant axial length difference between phakic and aphakic eyes.43 Others have found no significant change in axial length in eyes measured after cataract removal and 1OL implantation.37,63
One group noted an average increase of axial length postoperatively of 0.11 mm.64 When the measured postoperative axial length value was substituted in the preoperative measurement, however, they found no increased accuracy and concluded that the measured preoperative axial length was appropriate to use in 1OL formulas.
It is thus impossible at the present time to consider postoperative changes in the axial length of the globe in preoperative calculations of IOL power.
Simplifying assumptions are involved in the use of ultrasound to measure the axial length of a phakic eye. The actual velocity of sound through the crystalline lens may vary with the degree of cataractous change, becoming higher as the lens becomes more cataractous.30,38,65 An unusually high intratissue velocity of ultrasound in a very cataractous lens, for example, may lead to decreased cornea-retina transit time for the ultrasound beam and a falsely low axial length measurement. Hoffer30 has measured each component of the axial length individually, with the A-scan ultrasound unit reset for the particular speed of ultrasound in each tissue in the path of the ultrasound beam. (An average or estimated velocity of ultrasound in the lens must be used.) When compared with a single measurement with the A-scan unit set for an “average” tissue velocity for the entire eye, however, the more complex method was, if anything, less accurate.30 One investigator compared the accuracy of axial length measurements in phakic versus aphakic patients (for primary versus secondary IOL implants).52 No significant differences were noted between the two groups. This implies that any inaccuracy that may be introduced as a result of the variability in the speed of ultrasound in cataractous lenses is not significant.
Others have studied the ultrasound characteristics of cataracts.67 They found that the attenuation of ultrasound was related to the degree of lens hardness; the speed of ultrasound, however, was not significantly different in lenses of different degrees of “hardness.”
The speed of ultrasound used to determine axial length is an approximated average of the speed in the crystalline lens and the speed in the rest of the eye.68 Ultrasound travels at 1,532 m/sec through the aqueous and vitreous, and at 1,641 m/sec through the cornea and cataractous lens. Adjusting for the proportion of the eye transmitting at each speed yields an average speed through an eye of 1,555 m/sec. This approximation, however, may be less accurate in long or short eyes. In a short eye, for example, a higher proportion of the distance traveled is lens, through which the ultrasound travels faster. This would result in a shorter transit time and a lower measured axial length. Thus, the short eye may be measured as falsely short and the long eye may be measured as falsely long. This error is compounded by another study that revealed that long eyes have thinner lenses (4.5 mm) and very short eyes have thicker lenses (5 mm).69
Corrections to axial length measurement based on the axial length have been presented.68,70 Ultrasound travels through aqueous and vitreous at the same rate, 1,532 m/sec. The speed through the cornea and cataract is 1,641 m/sec. The “average” speed of sound through the phakic eye is considered to be about 1,550 to 1,555 m/sec, but obviously this number increases for short eyes (in which a greater proportion of the distance is within the cataract) and decreases for long eyes, which have relatively more aqueous and vitreous. Hoffer68 and Holladay70 have suggested that axial length measurement can be made more accurate if these factors are taken into consideration, and this may be especially important in short eyes. Holladay suggests measuring the axial length as if no lens were present, using an ultrasound speed of 1,532 m/sec. (If the A-scan is set at a different ultrasound speed, conversion is simply done. Suppose the A-scan were set at the “average” speed of 1,553 m/sec. Multiply the thus measured axial length by 1,532 or 1,553 to get the lower axial length that would result if the speed of sound were less because of the absence of the lens.) To this add 0.28 to account for the higher speed of sound in the lens and the resulting shorter-than-actual measurement (Hoffer suggests adding an additional 0.037 for a net add of approximately 0.32, to account for the increased speed of sound in the cornea as well (personal communication 2000) to get the true ultrasonic axial length. (In an aphakic eye, only 0.037 needs added for the cornea because there is no lens; such correction may be clinically insignificant in practice.) Using this axial length in a (theoretic) power formula may increase accuracy. The SRK/T formula may already include corrections to maximize IOL accuracy with the A-scan axial length as usually measured and, thus, may already incorporate this (or a comparable) correction.
Modifications are also available for aphakic or pseudophakic eyes.
When measuring the axial length of a pseudophakic eye, the IOL material must be considered. Because sound travels far more slowly in silicone than in polymethyl methacrylate (PMMA), an apparent axial length increase of 1.045 mm in eyes with silicone IOL may be noted if this difference in ultrasound speed is not considered. The average speed of sound in an eye with a silicone IOL is 1,476 to 1,486 m/sec, compared with 1,548 to 1,555 m/sec in an eye with a PMMA lens.68,71 Such estimations vary, of course, with the size of the eye, the power of the lens, and perhaps even the body temperature. Similar problems can occur when measuring axial length of a postvitrectomy eye filled with silicone oil. An artifactually longer measurement may be obtained if the speed of sound in silicone oil is not used.72 Some investigators have used 987 m/sec as the speed of sound in 1,000 centistoke silicone oil68,73 One approximated the axial length of silicone-filled eyes using the above correction, then remeasured the eye following removal of the silicone oil.73 The error in the axial length was less than 1%. Silicone oils of different viscosities will have different sound speeds and correction factors. Ultrasound velocities for eyes containing silicone oil or various IOL materials have been suggested.68
Conversely, falsely low axial length measurements have been reported in an eye with asteroid hyalosis as a result of confusingly strong echoes from the midvitreous.74 Others have confirmed falsely short axial length measurements in this situation and have found it more accurate to use the axial length measurement of the noninvolved fellow eye for IOL power calculations.75
The technique of ultrasound A-scan measurement that is used may also be a factor.30,31,32 It has been suggested that applanation methods of axial length determination indent the cornea and falsely shorten the axial length measurement.29,31,32,76 Measurements of axial length made with an applanation technique were, on average, 0.1 to 0.32 mm less than measurements made with an immersion technique.77,78 One investigator took multiple axial length measurements. He compared the accuracy of using the average reading compared with the longest value. Although there were similar results in the two groups, he suggested that the longest reading may be the single most accurate, because shorter values may result at least in part from corneal indentation.79
Posterior staphylomas may be present, particularly in longer eyes. One group used B-scan ultrasound to better avoid anomalous A-scan echoes from vitreous debris and to avoid staphylomas. They found a nonstatistically significant increase in the accuracy of the resultant refraction.80 Others have also noted decreased IOL accuracy in long eyes, particularly in those requiring negative power IOL.81 Their eyes over 27 mm were over-minused by 1 to 4 D, leaving the eyes with postoperative hyperopia. They recommend concurrent B-scan of all eyes longer than 27 mm.
A-scan axial length measurements showed less variability on retesting than ACD measurements did.78
It may be prudent to measure both eyes routinely; a malpractice decision in Louisiana faulted the ophthalmologist for not taking comparison axial length readings of the other eye as a check against erroneous measurement.82
Partial coherence interferometry is a new technique for measuring axial length.83 It is a method that does not require direct contact with the tissue being investigated. It measures echo delay and intensity using infrared light reflected back from internal tissue interfaces. Given that the velocity of light is too high to measure echo delay times directly, interferometric methodology must be used instead. This technique provides more precision and reproducibility than ultrasound. The patient must fixate a target; this thus ensures that the optic axis is being measured. The clinical usefulness of this technique is still undetermined. It is likely that a formula such as the SRK/T that already includes corrections for the vagaries of ultrasonic axial length measurement will need reformulation for axial length measurements made in this new way.
Other kinds of eye surgery may affect the axial length of an eye. One study noted a decrease in axial length following trabeculectomy.84 These were more pronounced in cases in which a large decrease in intraocular pressure was achieved (30 mm Hg) and in which antimetabolites were used. An average decrease of 0.46 mm was seen in these cases, at least partly because of an increased thickness of the choroid. Conversely, if these eyes then undergo cataract surgery, there may be an increase in axial length if the intraocular pressure rises. An average increase of 0.275 mm was noted in these cases. They suggest that a pretrabeculectomy axial length be used for IOL calculations rather than posttrabeculectomy axial length.
Scleral buckle surgery may result in an increase in axial length, resulting in a lower IOL power required.85
Measurement of Corneal Curvature
It has been stated that if the average of three readings in each meridian is used, the error is negligible.4 Errors in keratometry have been noted after wearing hard contact lenses.86 Even 2 weeks after use of hard contact lenses, patients had an increase of 0.79 mm in corneal measurements, resulting in an average decrease of 0.98 D in calculated IOL power. A malpractice case in Louisiana faulted the ophthalmologist for taking preoperative measurements on a patient who had only just removed his hard contact lenses on arriving at the office.82 The patient was not instructed to remove his contact lenses for a sufficiently long period (speculated to be between 2 hours and 2 weeks) before keratometric measurements were taken.
A postoperative difference may exist in the average keratometric readings (usually a slight flattening of the cornea secondary to the surgical manipulations.87 An average increase in the radius of curvature of approximately 0.08 mm (approximately 0.5 D flatter) has been noted after cataract extraction.87 Binkhorst compensates for this slight flattening by underestimating the index of refraction, using n = 3 rather than 1.336.4 Other studies have revealed a postoperative steepening of the cornea of 0.16, 0.11, and 0.14 D, respectively.34,38,76 Hoffer compared large numbers of phakic, aphakic, and pseudophakic eyes.43 He found a corneal flattening of 0.16 D in aphakic compared with findings in phakic eyes. Interestingly, no significant corneal flattening was noted in the pseudophakic eyes. Others have found no significant change in keratometric measurements following cataract removal and IOL implantation.63,88 Following scleral buckle surgery, the corneal curvature may increase.85 An error of 0.1 mm in radius of corneal curvature results in a postoperative refractive error of approximately 0.50 D.4 In otherwise healthy patients, computerized videokeratography was, if anything, inferior to standard keratometry in obtaining accurate measurements.89
The problem of selecting which keratometry reading to use is more complex if penetrating keratoplasty is to be combined with IOL implantation. One group found no correlation between preoperative and postoperative keratometry readings.90 Nevertheless, their results were more accurate using preoperative keratometry readings or even using readings from the other eye, compared with selecting an IOL power without using a keratometry value from either eye. Another group also noted that penetrating keratoplasty produced marked changes in postoperative corneal curvature and power.91 They found it impossible to develop a single formula for all surgeons to predict IOL power accurately in these cases. Results were quite significant from surgeon to surgeon, perhaps owing to differences in surgical technique and suture patterns. In the analysis of results, it was found that the axial length was the single most important factor contributing to the prediction of IOL power. Interestingly, the preoperative keratometry reading figured into an SRK-like formula as a positive term; that is, the higher the keratometry reading, the stronger the IOL that was needed. This was explained by the negative correlation, in this series, between preoperative and postoperative keratometry.
Another group suggested using 106% of the keratometry reading of the donor, or an arbitrary value of 45 D (for a 7.5-mm graft placed in a 7-mm recipient bed).92 They also noted no significant change in axial length after surgery and pointed out that an alternative is the deferral of IOL insertion until a second procedure, delayed until after the new keratometry readings have stabilized. Another group obtained best results using the average postkeratoplasty keratometry readings for IOL calculation.93,94 The average keratometry readings 1 year after transplantation were similar, regardless of the differing preoperative keratometry readings.94 The Binkhorst, SRK, and personalized regression formulas all gave similar accuracy.94
Patients who have had corneal refractive surgery present unique cataract surgery problems. One group reported four patients having IOL implantation after previous radial keratometry.95 Standard keratometric measurements tended to overestimate the true corneal power, resulting in an underestimation of the required IOL power, possibly because the keratometer may be measuring a more peripheral portion of the cornea that does not fully reflect the flatter central cornea. The Binkhorst and Holladay theoretic formulas were more accurate than the SRK.11 The most accurate corneal curvature to use for IOL calculation was obtained by taking the prerefractive surgery keratometry readings and subtracting the surgical refractive change from that. One investigator found superior IOL accuracy by using computerized videokeratography to measure corneal powers after radial keratotomy.96
After IOL implantation, postoperative corneal flattening was noted, some of which persisted. Severity of this flattening was inversely proportional to the time interval between radial keratometry and cataract surgery, possibly because long-term healing of the radial keratometry incisions may partially blunt the edema-induced hyperopic shift that occurred after IOL surgery.
After photorefractive keratectomy (PRK) for high myopia, the measured postoperative corneal keratometry readings were not most accurate for IOL power calculations.96,97,98 Refraction-derived measurements were obtained by using preoperative keratometry readings and correcting them for the measured change in refraction (at the corneal plane). These numbers proved to be more accurate for IOL calculations.
Hoffer99 has contrasted four ways of measuring corneal power in eyes that have had refractive surgery.99 The first is standard keratometry. This may measure corneal power at a 3-mm distance from the corneal center and may not fully represent the new more central modified zone. The second is using the refractive history and preoperative keratometry readings. Modify the preoperative keratometry readings by the refractive change postoperatively (at the corneal plane) and use this as the keratometry readings for the IOL power. The third is the contact lens over-refraction method. Take the postoperative refraction, then place a contact lens of known power on the eye and re-refract. Use the base curve of the contact lens for IOL calculation, modified by any change in the manifest refraction and corrected for the power, if any, in the lens. (Another investigator100 points out that this over-refraction method has the advantage of detecting visual loss caused by irregular astigmatism rather than cataract, which could conceivably alter the decision to perform cataract surgery in the first place!) The fourth method is to use videokeratography and measure more centrally than is usually possible with standard keratometry.
One study found that direct measurements of the cornea after PRK underestimated corneal flattening by 24%.101 Another investigator had a decentered ablation zone after PRK that resulted in a too-steep keratometry reading.102 They recommended using the spheric equivalent refractive change (at the corneal plane) to obtain corneal keratometry readings for IOL calculation. Another investigator had a decentered ablation zone that resulted in a too-steep keratometry reading.
Measurement of Anterior Chamber Depth
The depth of the anterior chamber can be measured by instruments that can be incorporated into some slit lamps (pachometry); alternatively, it can be calculated indirectly by the method of Fyodorov et al.20 The depth of the anterior chamber has been noted to decrease progressively with age at the rate of approximately 0.1 mm per decade, probably owing to progressive swelling of the lens.4,44 ACD is also related to the degree of ametropia.44 The anterior chamber is 0.06 mm deeper for every diopter of myopia. Thus, an average -6 D myope is likely to have an ACD 0.6 mm deeper than a +4 D hyperope, all other factors being equal. A similar increasing ACD with increasing myopia has also been noted by Hoffer.43
An error of 0.1 mm in estimating the ACD results in a postoperative refractive error of approximately 0.1 D.4 Increasingly, however, the trend has been against measuring ACD values for each patient. It has been emphasized that what the lens formula requires is a predicted postoperative value for ACD (or lens position) rather than the measured preoperative value.103 Hoffer’s results for two-loop prepupillary lenses were not as accurate using the measured ACD in his calculations as were those measuring the ACD and using one of three predetermined values.30 Shammas104 compared preoperative and postoperative ACD in eyes with anterior chamber lenses and concluded that no significant difference existed in postoperative ACD among eyes classified into several different ranges of preoperative ACD measurements.104
Hoffer30 measured the position of the posterior capsule preoperatively and after extracapsular surgery in 30 patients.30 He found no correlation between the preoperative and postoperative measurements. Realizing that the important measurement is not the ACD in itself but rather the postoperative position of the IOL, Hoffer measured the position of the posterior capsule (supporting a posterior chamber lens) and analyzed factors that could be used to predict it.105 No relationship existed between the position of the posterior capsule and the patient’s age or corneal keratometry, nor was there a relationship between the preoperative position of the posterior capsule and the axial length. A correlation was found, however, between the posterior capsule position postoperatively (postoperative ACD) and the axial length L. Hoffer stated that the ACD used to calculate IOL power should reflect the actual postoperative lens position.
Another group measured the distance between the cornea and posterior lens capsule in 60 eyes before and 3 months after posterior chamber IOL implantation.106 They found the postoperative posterior capsular position to increase with patient’s age, ACD, and axial length.
In contrast to the case of a posterior chamber lens, another investigator applied the techniques of regression analysis to study the postoperative position of an anterior chamber lens.107 For an anterior chamber lens, the postoperative position (postoperative “ACD”) was not correlated with the axial length but was related to the preoperative ACD, corneal curvature and diameter, and thickness of the cataract.
There are other sources of error as well. First, the thickness of the cornea is discounted in all these calculations, and any refraction that occurs at the cornea–aqueous interface is not considered. Second, the IOL is considered as a thin lens, whereas actually the two principal planes of the IOL do not coincide. Light may be thought of as entering the lens at its first principal plane and leaving at the second, with no angular change in the light rays (unit magnification) in the interim.108 Thus, the measured axial length of the eye should be reduced by an amount equal to the distance between the two principal planes. For a convexoplano lens, this distance between principal planes is one-tenth of the lens thickness (e.g., 0.05 mm in a 0.5-mm thick lens,0.08 mm in a 0.8-mm thick lens).4
The ACD is usually determined as the distance between the vertex of the cornea and the vertex of the lens. More rigorously, the measurement should reflect the distance between the corneal vertex and the first principal plane of the lens.
Finally, it is possible that the surgical technique itself may have an effect on the postoperative ACD. It was noted that the ACD may be related to the size of the capsulorrhexis. At 90 days after surgery, eyes with a 4-mm capsulorrhexis had a greater anterior chamber than eyes with a 6-mm opening.109 The larger capsulorrhexis may allow more anterior bowing of the IOL and a consequent shallower ACD.
Lens fixation and orientation may have an effect on the ACD. Introduction of capsulorrhexis and more stable fixation in the bag was shown to result in more stable anterior chamber positioning and more accurate IOL power predictions.110 One investigator compared approximately 50 patients with standard in-the-bag lens fixation, 50 with planned out-of-the bag IOL after previous extracapsular surgery, and 50 patients with transscleral suture-fixated IOL. The IOL was noted to be more anterior with out-of-the bag and scleral suture-fixated IOL compared with in the bag fixation.111 This resulted in a myopic shift in the refractive result. In addition, IOL decentration, which occurred with scleral suture fixation, also contributes to a postoperative myopic shift. IOL tilt of greater than 10 degrees was seen in 11.5% of the suture-fixated IOL; such tilt results in an increase in effective IOL power and contributes to a postoperative myopic shift. These authors recommended dropping 0.5 D from the calculated IOL power in cases in which planned sulcus fixation (out-of-the bag) or scleral suture fixation is planned.
Later YAG capsulotomy may change the effective ACD.112 Capsulotomy caused a backward movement of the IOL, more pronounced with plate haptic IOL than with one-piece PMMA and three-piece foldables. The resultant hyperopic shift was not clinically significant.
Considerations After Photorefractive Surgery
In eyes that have had photorefractive surgery (PRS), IOL power calculations have been more challenging, which may be owing to several causes:
1. Incorrect Measurement of Corneal Power. The anterior corneal curvature may be measured incorrectly because of changes in this curve and just where on the cornea the measurements are taken. Keratometry assumes that the anterior and posterior corneal surfaces are nearly parallel, with the posterior surface approximately 6 D steeper than the anterior surface (thus, contributing -6 D to the total corneal power).113 This assumption is automatically factored in with traditional measurements of corneal keratometry (that is, 6 D are subtracted from the anterior corneal measurement.). This relationship is no longer true after the anterior corneal surface or curvature has been modified by photorefractive laser techniques. It has been noted that the effect of laser ablation on IOL power calculations varies with the amount of treatment.114 It should be noted that after PRS, the cornea is more aspheric—the central corneal power is flatter (myopic PRS) than the paracentral cornea. If the keratometer measures the paracentral cornea, the measurement may not accurately reflect the refractive status.
Another source of error is present in myopic kerotorefractive patients. Thinning of the cornea can result in limited corneal ectasia and increase in the posterior corneal curvature. Standard keratometers will overestimate corneal power in previously myopic eyes and underestimate it in previously hyperopic eyes. (Note that this discussion does not apply to patients having radial keratometry [RK]. In post-RK eyes, both the anterior and posterior corneal surfaces are flattened.) More complex corneal mapping technology (as compared with standard keratometry) may reduce these errors, but experience with this technology is still evolving. (The “clinical history” method eliminates the need to measure the postkeratorefractive cornea. The change in refraction is assumed to result from corneal changes, and the corneal power is modified accordingly. For example, if the patient is now 5 D less myopic (at the corneal plane), the assumption is that the corneal power is 5 D flatter.)
2. Error in Calculating the Effective Lens Position (ELP). Many third- and fourth-generation formulas use the ELP. (The Haigis formula is an exception, because it does not use the keratometry reading for ELP prediction.115) Using the postkeratometric keratometry values may underestimate anterior chamber depth and ELP.
Double-K Method of IOL Calculation
One interesting approach to the postkeratorefractive eye is the so-called double- keratometry (double-K) method,119 in this case a modification applied to the SRK/T formula. A third-generation IOL formula (i.e., Hoffer Q, SRK/T, Holladay) works in two steps. First, it determines the ELP using the axial length and keratometry measurements. The ELP (and the calculated anterior chamber depth) should not change following PRS. If the post-PRS K readings are used to calculate the ELP, an incorrect value will be obtained. The anatomic anterior chamber depth and ELP should not be affected by a change in the corneal surface contour. Using postoperative keratometry s to calculate the IOL power will result in an erroneously low ELP and, thus, IOL power, resulting in a hyperopic post-IOL refraction.
The double-K technique provides a method to bypass this error. It uses the preoperative keratometry in the first part of the IOL calculation, the part that determines a value for the (anterior chamber depth and) the ELP. Then it uses the postoperative keratometry for the vergence calculations in the second part of the formula to determine IOL power. The postoperative keratometry values were determined by the clinical history technique. Patients with more than a 2 D myopic shift (possibly caused by increasing nuclear sclerosis) were excluded in the report. (Presumably, as other more accurate methods of measuring the “real” postoperative keratometry evolve, they may be substituted for the clinical history determination used in this report.) Although this technique requires knowledge of the preoperative keratometry values, it improves the accuracy of IOL power determination in PRS eyes.
Types of Intraocular Lenses
Piggyback Intraocular Lenses
An eye with a shorter axial length requires a stronger IOL. As IOL powers become too high, however, the lens becomes too spheric and image quality decreases. Using two lenses to obtain a needed high-power correction results in an optically superior image compared with that obtainable by a single lens of required power.
A mathematic analysis of image quality of piggyback lenses was performed.120 The axial image quality of piggyback lenses was superior as determined by modulation transfer function analysis, especially at low and middle spatial frequencies, which are those used in daily visual tasks. There is also a greater tolerance for manufacturing and positioning errors with the piggyback technique. Both single lens and piggybacking, however, achieved theoretic Snellen vision of 6/5 (with theoretic optimal lens shapes, which may not necessarily conform to the lenses commercially available).
Thus, for short or nanophthalmic eyes, so-called piggyback IOL represent a viable solution.121 Holladay and Giles122 implanted six such lens pairs in eyes ranging from 15 to 20 mm in axial length. All three third-generation formulas resulted in postoperative hyperopia of about 5 D; the SRK II resulted in an error of about 11 D. This may have occurred for several reasons: First, error of axial length measurement is especially damaging in shorter eye calculations; a given error is higher proportionately in a smaller eye. Furthermore, errors in axial length translate to larger IOL power differences as the IOL powers increase. Second, all third-generation formulas shorten the expected ACD as a function of axial length; for very short eyes, they all predict the ACD to be too shallow and the IOL to be too far from the retina, leading to the calculation of a too-weak lens. Third, the position of the IOL may be changed. In a piggyback lens system, measurements showed that the anterior IOL was in the normal position, whereas the posterior one was more posterior (thus, the more posterior lens was “too weak” for its position). Holladay also points out that we should distinguish the normal short eye, with a normal anterior segment but a short posterior segment, from the nanophthalmic eye with symmetrically short anterior and posterior segments. He proposed modifying IOL calculation in these cases to include determination of the size of the anterior segment, using the white-to-white corneal diameter, ACD, and lens thickness as well as keratometry and axial length.
Piggyback minus lenses have been used in eyes of long axial lengths alone or combined with high corneal curvature123 to achieve minus powers commercially unavailable in a single lens.
Piggyback IOL can also be inserted in two stages, with the second IOL inserted (in the ciliary sulcus) to correct an undesirable refractive result following the initial IOL implantation. If the second lens is placed posteriorly (by surgical error), the resulting positions are unstable and unpredictable and the refractive results are less predictable.124
Refractive results in adding a piggybacked IOL as a second procedure should be superior to that of an IOL exchange for several reasons.124 First, the power of the second IOL is based only on the postoperative refraction. Second, the surgeon cannot be certain that an exchanged IOL would be in exactly the same plane as the IOL it replaced. Third, the accuracy of the power labeling of the first IOL is irrelevant, because of the first reason. Fourth, these added IOL tend to be of lower power, and vergence-distance changes are less important with lower power lenses.
One occasional curious finding in piggyback lenses is an apparent increase in the depth of focus. This may result from contact between the two lenses,125 with a slight flattening in the zone of contact. This would result in a decrease in the optic power of the IOL with resultant hyperopia. The power in the peripheral lens area, however, would be unchanged. In three eyes with acrylic IOL, a difference was seen of 3.0 to 5.5 D between the central contact zone and the peripheral noncontact zone.126 Obviously, spectacle correction of the resulting hyperopia would be needed to allow the patient to take advantage of the increased depth of focus, unless initially the patient was overcorrected several diopters. Late hyperopic shifts have similarly been noted in piggyback lenses.127 An alternate reason for this could be a posterior displacement of both IOL, but to explain the observed hyperopic shift a movement of as much as 1.5 m would be necessary.
Toric Intraocular Lenses
It may be possible to correct a part of a preexisting regular astigmatism with an IOL. A cylindric correction of 2 or 3 D was incorporated into IOL implanted in 47 patients.128 This corresponded to an acylindric effect at the spectacle plane of 1.33 or 1.98 D. Another investigator implanted lenses with 2, 3.5, or 4 D of toric correction in 37 eyes and found the refractive effect to be 60% to 80% of the power at the IOL plane.129
Some 130 eyes had toric IOL implanted.130 These eyes had at least 1.5 D of both corneal and refractive cylinder. A 2.00-D toric lens was used for a 1.5 to 2.25 D cylinder, and a 3.5-D cylinder was used for eyes with between 2.25 and 3.5 D of preexisting cylinder. These eyes were compared with 51 similar eyes which were instead treated with spheric IOL and limbal relaxing incisions. No significant difference was seen in postoperative uncorrected vision, although a trend to better vision was noted in the toric IOL group. Respectively, 84% and 69% of the toric group had uncorrected vision of at least 20/40 and 20/30, whereas the spheric IOL group had 76% and 51% at these levels. The refractive cylinder was significantly smaller in the toric IOL group; however, 12 eyes (9.2%) of the toric group required a second procedure to correct rotational misalignment of the IOL (because of patient dissatisfaction and a rotation of at least 30 degrees). In fact, with the lens design used, 18% of eyes showed IOL rotation of 20 to 40 degrees, with 7% showing rotation of 40 degrees or more. The authors concluded that toric IOL present a viable method to correct preoperative astigmatism; obviously, improvements in IOL stability will reduce the need for secondary procedures.
The optics may be somewhat more complicated than with spheric IOL. It has been pointed out that, in deciding on toric IOL, the clinician should rely on the keratometric cylinder and not the refractive one.131 The refractive cylinder may include toric effects of the natural crystalline lens, which will no longer be operative after cataract removal. The best way to measure the needed toricity at the IOL plane is to calculate the IOL power for each of the two corneal powers; the difference is the amount of toric correction needed at the IOL plane. Obviously, unlike the case of spheric IOL, the correct orientation of the IOL is critical. The lens must be aligned with the preoperative cylinder. A beneficial effect still exists even if the lens rotates somewhat, as long as the lens is not more than 30 degrees off axis. Although some postoperative axial shift occurred, the one-piece plate lens appeared to stabilize by 2 weeks after surgery.129
Phakic Intraocular Lenses
Intraocular lenses have been developed for insertion into phakic eyes. Some are designed for anterior chamber placement, angle supported,132,133 or clipped onto the iris,134 whereas others are designed to be inserted in the posterior chamber in front of the natural crystalline lens.135 Some have been tried in children.136 To calculate the IOL power for a phakic eye, the preoperative refraction (and vertex distance) and corneal power are needed.137 Because this requires no assumptions of average ultrasound speed or crystalline lens thickness, its accuracy should exceed that of IOL replacement of the natural lens. For a minus power anterior chamber IOL of 10 D or less, there is no improvement in accuracy in calculating the ACD versus using a constant value based on the IOL type.
Posterior chamber phakic IOL have been used in children for the treatment of anisometropic amblyopia.138
Accommodation and Intraocular Lenses
Because it is a constant shape, the IOL does not change its focus (accommodate) by modifying its contour, as does the natural crystalline lens. It is possible, however, especially in young patients, that some pseudoaccommodation may occur by movement of the IOL itself.139 The study measured 45 eyes of patients aged 12 to 19 years. With attempted near vision, anterior movement of the IOL was measured with A-scan ultrasonography. The amount of pseudoaccommodation was greater than could be accounted for by the IOL movement alone. This pseudoaccommodation, however, was significantly related to the amount of IOL movement that occurred. No relationship to the patient’s age (in this group) or the refractive error was noted. As would be expected, pseudoaccommodation is inversely related to pupil size.140
One type of IOL is designed to provide pseudoaccommodation through the mechanism of anteroposterior movement of the optic on near and distance vision. This IOL has a peripheral bulging ring that is supposed to push the optic forward during the effort to accommodate. A study compared a group of patients receiving such a lens with a comparable group receiving a foldable silicone lens.141 ACD was measured after cyclopentolate instillation (ciliary relaxation) and again after pilocarpine installation (ciliary contraction). The accommodating IOL showed a significantly greater axial movement; however, the difference in the measured pseudoaccommodation between the two groups was not significant.
An attempt to refill an evacuated capsular bag with injectable silicone or other deformable material has been studied in animals. This may have the potential to allow some degree of pseudoaccommodation142; however, many questions remain to be answered before it will be known whether this will be a viable technique in humans of presbyopic age.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree