Physical Optics
David Miller
Paulo Schor
As eye doctors, we measure the optical properties of the eye and study its structures. To enable us to understand our instruments, we are taught that light acts as a stream of tiny particles, moving in straight lines that we call rays, and that these rays follow the laws of geometry.
Geometric optics, however, cannot explain why the sclera is white, the iris blue, and the fundus red, or why a cataract is opaque. Study of physical optics is needed to answer these questions. One might think of geometric optics as the workhorse of an ophthalmic practice, whereas physical optics can provide the intellectual excitement.
The discoveries of physical optics are rich in the secrets of the universe, and the unraveling of these secrets has allowed us to harness the major forces that surround us.
HISTORY
The subject of physical optics seemed to gather substantial momentum in 1666, when Isaac Newton directed a shaft of sunlight through a glass prism and collected the transmitted light onto a white surface. The prism had broken the white light into the colors of the rainbow. Although Leonardo da Vinci had actually performed the same experiment in his workshop in Milan 200 years earlier, he feared that the ruling powers might consider the work blasphemous and so he told no one, only recorded the findings in his journal in a mirror writing code. Fortunately, Newton was able not only to report his work, but also to speculate as to its mechanism. Newton had already stated that light rays were a stream of particles, a theory that adequately explained how lenses work. To this he added that white light was simply a combination of many colors, and that the prism refracted each color differently so as to make them all visible.
To some, the presence of many colors in white light suggested that the colored rays had unique qualities. Christian Huygens, a Dutch contemporary of Newton, preferred to liken the process of light to the process of sound waves. Since the pitch of a sound depended on its wavelength, he believed the different colors of light also had different wavelengths. Any new theory of light, however, would also have to explain the facts of geometric optics. Thus, he imagined a light beam as composed of many small, circular wavelets that interacted with each other to form a wavefront. Unless it were to strike an obstacle, this wavefront would travel forward in a straight line. If the wavefront were to strike a piece of glass obliquely, one end of the wave front would strike the glass first. The progress of that end of the front would then be slowed down in comparison to the other end, which would still be in air. In this way, the entire front would be bent, making a smaller angle with the normal. Huygens further suggested that each wavelength, upon entering glass, traveled at a different speed. One could say that he pictured the longer wavelengths as skipping with long strides and the shorter wavelengths, such as violet and blue, as moving more slowly, with short mincing steps, and so were refracted more.
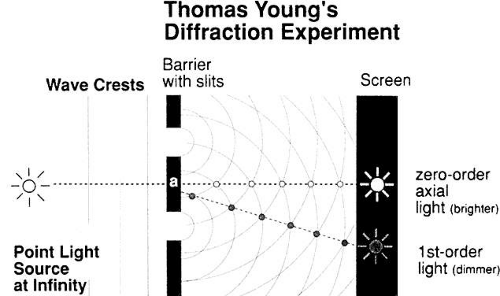
The wave theory also explained why a parallel beam of light seemed to diverge slightly as it passed through a small hole, and why light striking an opaque object cast shadows with indistinct edges.
Recall that Huygens pictured every point on a wavefront as a potential source of a series of waves in all directions, if the wavefront interacted with an obstacle. Thus, as a beam of light goes through an aperture, all the diverging wavelets are cancelled out by their neighbors to the right and left, and only the forward-directed waves are left, with one exception: the edges of the wavefront. At the right end, a right-sided wave has no right-sided neighbor on its extreme side. Thus, the edge of the beam veers sideways. It is almost as though the edge ray meets a friction between its one side and the edge, causing an apparent drag that forces the ray to veer off course. Again, the size of the wavelength is related to this edge effect: the longer the wavelength, the greater the diffraction. This phenomenon is exploited to produce the wide spectrum of colors in modern spectroscopes. A series of closely placed slits (thus yielding many edges) in the form of a diffraction grating produces a vivid spectrum in which red is bent the most and violet is closest to the center. This spectrum is the reverse of that produced by a prism, in which the shortest wavelength (violet) is refracted the most. The edge effect can be a problem in photography, when a large f number (small iris opening) is used to yield a greater depth of field or, as we will see, when the pinhole disc is used to improve visual acuity.
WAVE MOTION
The historical evidence we have recounted so far describes light as a wave motion. This means that when a wave runs over the surface of the water, a piece of cork floating on the surface will bob up and down but will not travel forward (Fig. 3). If you jiggle a rope, the hump moves forward but not the rope. These examples describe the essence of a wave as a state of motion that travels forward, forcing vibrations in its path. What, then, vibrates in the direction of a light beam to give the wave? Aristotle suggested that a universal ether filled the universe and that it vibrated. The French physicist Fresnel expanded this idea and pictured ether as a very thin elastic substance that even filled a vacuum. When a portion of the ether was distorted at right angles to a light beam, it snapped back immediately, even though light was traveling at a speed of 186,000 miles/second. It is ironic that by the mid 19th century, almost all the concepts of Aristotelian physics had been discarded, yet the physicists had no choice but to cling to the concept of ether if light was to be considered a wave.
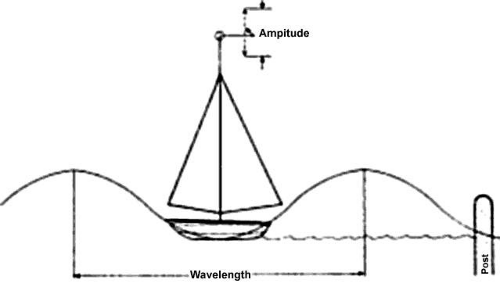 Fig. 3. A moored boat bobbing up and down on the waves does not move forward. If a marker is attached to the mainsail, it will chart the amplitude of the wave. |
The new idea that would eliminate the mystical ether was supplied by the brilliant Scottish theorist James Clerk Maxwell. Maxwell had been impressed by Michael Faraday’s experiments, which had shown that both electrical energy and magnetism could be transmitted without wires or contacts. Faraday had further shown that a varying magnetic field could induce an electric current, and that an electric current could induce a magnetic field.
Maxwell was fascinated by these related forces, which seem to function at a distance. He took Faraday’s findings and developed four differential equations to describe the quantitative interrelationship between electricity and magnetism. The equations placed the two forces at right angles to each other in a single electromagnetic field. The equations also suggested that if the changing electrical field induced a changing magnetic field, which, in turn, induced a changing electric field, the resulting electromagnetic radiation had wavelike properties. The equations also predicted the velocity of these radiations to be the same as the speed of light! Although Maxwell embraced the ether theory of the day, we can see that these equations implied that the wavelike properties of light were the same as the oscillating values of an electromagnetic field. Thus, we can imagine the oscillating field of a light beam as oscillating changes in the geometry of space. The concept of an oscillating field could take place in a vacuum, and the unrealistic ether could be abandoned.
Scientific thought has a strange way of going in cycles. Just when the particle theory of light was completely replaced by the wave theory, a type of light particle called a quantum was identified, which appeared to be the true representation of light.
QUANTUM THEORY
At the close of the 19th century, interest focused on radiations beyond the visible (i.e., ultraviolet, infrared, radiowaves). This work involved the heating of black elements, since black theoretically absorbed all radiation falling upon its surface. For example, the German physicist Wien studied the manner in which a black-body radiator glowed as it was heated. As the heat rose to 3000 K, the body glowed red; at 5000 K to 6000 K, it glowed yellow; and at more than 8000 K, the radiator glowed blue. Obviously, the heat had been converted to light, but how? At the beginning of the 20th century, the German physicist Max Planck had not only solved this problem, but in so doing had unearthed one of the most important physical principles of the 20th century. Planck had set about carefully measuring the radiant energy and distribution of wavelengths emitted as a black body was heated to higher and higher temperatures. Certainly, as the radiator glowed from red to blue, the frequency of the waves emitted increased. But careful measurement of the radiated energy showed that it climbed at a slower pace compared with the change in frequency. What was happening? In a lecture given in 1900, Planck said, “I find myself driven almost against my will to the assumption, unsuspected till now in physics, that the electromagnetic energy emanating from a source of heat is not continuous, but divided, as it were, into definite portions or quanta.”1
The quantum theory remained half noticed, and not quite believed, until 1905, when Einstein used it to explain the photoelectric effect. For his famous equation, Einstein assumed that electrons on the surface of a metal emitter absorbed light energy, one quantum at a time. If the energy of the quantum was that which was precisely needed to overcome the forces holding an electron to the surface, the electron would be set free and a trickle of current would develop.
The quantum theory applies to the atom as well. It states that the energy of the atom assumes a certain definite spectrum of values characteristic for that species of atom. Usually the atom is in its lowest energy level, or ground state. When the atom is exposed to light of a frequency such that the energy of the photon equals the energy difference between the excited and ground states, the photon is absorbed, producing an excited state. One may also say that the light is in resonance with the atom. In a fraction of a second, the atom will fall back to its previous energy state and emit the energy difference. Einstein realized that every metal is resonant with a critical wavelength for this photoelectric effect.
ATOMIC STRUCTURE
If light quanta and electrons interact, they apparently are of a similar magnitude. Is light so fundamental as to be connected to the very structure of the atom? But what is the atom? In 1913, the Danish scientist Niels Bohr presented his model of the structure of the atom. It included a positively charged central nucleus surrounded by shells of swirling negative electrons. He went on to suggest that light had its origin in the atom. He pictured the various shells of electrons as behaving almost like a slot machine, which takes a variety of coins (i.e., the dime slot only takes a dime, the quarter slot only a quarter). The different electron shells will accept only a quantum of energy that corresponds with the innate nature of the shell. When energy is absorbed, an electron of one shell is raised to a new permitted orbit, where it stays for approximately a hundred millionth of a second. As the electron falls back to its original shell, an electromagnetic wave is released. The dimensions of the released wave (i.e., wavelength) are related to the dimensions of the electron shells involved in the interplay.
COLOR
Using this concept, one can explain why certain pigments take on the colors that they do. Molecularly speaking, pigments usually have a ring structure. Electrons move more freely within a ring structure than within a branched molecule. Therefore, the electrons, which are also considered to have wave properties, are allowed to have longer wavelengths, or lower frequencies, in ring molecules. Most molecules resonate with ultraviolet light; however, because of the Planck relationship and the ring structure of the molecule, pigment molecules resonate in a lower energy state and thus absorb visible light. The surface of pigment molecules has been likened to a sieve, and light falling on them to a series of colored balls, each colored ball being a different size. In the case of a red dye, all the colored balls but red would drop through the holes of the sieve and become absorbed, later to radiate in the invisible infrared. The red balls, however, accumulate on the sieve surface. Thus a molecule of pure red dye has its electron shells so arranged that quanta of all the visible wavelengths but red fit snugly into its dimensions and become absorbed. The red, on the other hand, is backscattered to the observer’s eyes.
The physical dimensions of light and matter can also explain light scattering. If light strikes a structure larger than 1000 nm, the light is absorbed. If the structure is less than 1 nm, the light passes by unaffected. However, if the object has a size between 1 and 1000 nm, light will be absorbed and re-emitted as a ray of similar wavelength, but in a different direction. This phenomenon of light scattering takes place among the water particles of a cloud and is responsible for the clouds’ opaque appearance. (In a subsequent section of this chapter, the principles of light scattering will help unravel the behavior of the edematous cornea and the cataract.)
INTRAOCULAR LIGHT SCATTERING
DEFINITION
Picture a shaft of light piercing a dusty room. The physicist sees each dust particle as an agglomerate of many atoms and molecules. These, in turn, are composed of negatively charged electrons and positively charged, heavy nuclei. When a stream of photons is absorbed by a dust particle, the electric field in the light beam can be pictured as exerting an oscillating force on both the nuclei and the electrons. The heavy nuclei remain unmoved, but the electrons are displaced from their normal orbits and move rapidly back and forth in synchrony with the driving electric field of the light beam. In so doing, light waves are radiated in all directions. The observer sees the shaft of light because his eye detects the sidewise-scattered light from each particle. If the room were clean of all dust or scattering particles, the beam would be invisible to the observer.
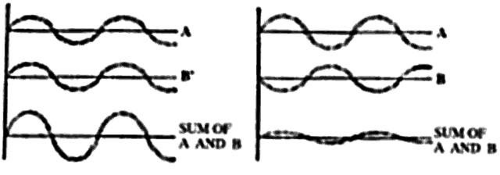
The situation becomes a bit more complicated when the scattering particles are spaced closer together than dust in a room. Certainly, each scattering element radiates light waves in all directions, and the total scattering is the sum of all the waves. But here is where a complication arises. Waves may add constructively or destructively. At any one observation outpost, the net amount of light reaching that point is determined by the sum of the constructive and destructive interference of all waves crossing that point.
Let’s stop for a moment for a definition. The quantity that describes what point each wave is in its oscillation cycle is called the phase of the wave. The key concept in this definition is that the difference in phase between waves depends, in part, on the spacings of the scattering particles in comparison to the wavelength of light. If, for example, two scattering particles are spaced by distances comparable to one half the wavelength of light, the two scattered waves will be 180° out of phase and the waves will then cancel each other, giving no electric field at the observation point. If, however, two particles are spaced at distances that are small in comparison to the light wavelength, the phases will nearly be the same, and the scattered field will have an amplitude twice as large as each wave individually. Therefore, the final summation of all scattered waves will give a result that depends both on the relative positions of each scattering particle in comparison to the wavelength of light and on the direction of the scattered waves. For example, light is completely transmitted through a transparent medium such as water because the water molecules are tightly packed. This means that all the waves scattered sideways from each of the molecules travel a longer distance and are out of phase with each other and thus interfere destructively with one another in all directions, except the forward direction. In water, side-scatter is eliminated, but forward-directed light waves reinforce each other because their straight-ahead paths have similar lengths.
Another factor important in scattering is the overall regular arrangement of the scatterers. For example, the lens of the normal eye is made up of protein and physiologic fluid. The lens proteins are tightly packed in an orderly fashion, and there is very little change in the density of the scattering particles from point to point in the lens. Thus, the lens is transparent. If a clear lens homogenate is mixed with water, the proteins are dispersed and the density of the proteins fluctuates markedly, producing a random pattern. The result is a great deal of scattering and a milky-appearing solution.
In summary, the relationship between the size of the wavelength of light involved, the spacing of the scatterers, the size of the scatterers, and their arrangement determines the total scattering from a medium. This interaction is analogous to running one’s finger over a smoothly polished surface. The surface feels smooth if the irregularities are small in amplitude and are spaced by distances that are small in comparison to the spacing between the pressure-sensitive receptors on the fingertips. The sense of touch has a certain resolving power and cannot respond to small-scale fluctuations. In the case of light and scattering, if the scattering medium has periodic fluctuations in arrangements of scattering components larger than the wavelength of light, then these can be sensed by light waves and scattering can occur. If the spacings of the scattering components of the media are shorter than one half the light wavelength, little scattering can occur.
It is time, now, to apply our theoretic understanding of light scattering. However, in order to explain some natural phenomena we will need to cover one more theoretic point. Lord Rayleigh showed that when light strikes atmospheric particles (particles smaller than the wavelength of light), the amount of light scattering is inversely proportional to the fourth power of the wavelength. Since the blue end of the spectrum is half the wavelength of the red end, the blue end is scattered by a factor of 24 or 16 times the amount of the red end. This seems logical, since small particles should interact more completely with smaller wavelengths.
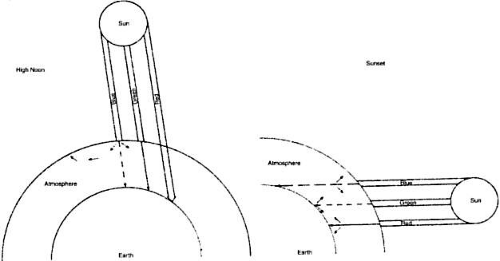
At high noon, the sun’s rays pierce the atmosphere in a perpendicular fashion (Fig. 4). Thus the shorter wavelengths of the sun’s spectrum are more heavily scattered by the atmospheric particles, which splash the color blue all over the sky. This takes some of the blue away from the sun’s own appearance, and it looks yellowish. At sunset, the light strikes the atmosphere at an angle and thus must travel a longer distance through the atmosphere (see Fig. 4). The additional particles scatter not only blue but also a significant amount of the longer wavelengths, and the sun’s color goes from yellow to orange to deep red.
When you look at the lens of an elderly patient through the slit lamp, you will notice that the reflection from the anterior capsule is blue-white, whereas the reflection from the posterior capsule is a golden yellow. The double passage of light through the lens has resulted in a loss of blue light due to light scattering, producing the yellow reflection. The more nuclear sclerosis present, the yellower is the reflection. Thus we can think of the crystalline lens as a minus blue filter, because of both its yellow pigment and its preferential scattering of blue light.
This concept of the lens as a minus blue filter was suggested by Dr. Aran Safir2 and helps to explain why the optic nerve looks more yellow in the phakic eye than in the aphakic eye. In fact, to the medical student, the blue-white appearance of the optic nerve in the aphakic eye may be confused with optic atrophy.
In scleral tissue, we note that the collagen fibers are much larger than those in the cornea. Both the collagen diameters and the spacing between fibers are comparable to a light wavelength. Much scattering occurs in the sclera, resulting in an opaque appearance.
It might be helpful to return to nature for a moment and review what happens when a sunbeam strikes a cloud. Clouds are made up of air and water droplets, both of which are transparent; however, they differ in their optical indices of refraction. Air has a refractive index of 1 and water of 1.333. Thus, these two components, each clear by themselves, produce substantial scattering when the droplets of water are large enough to interact with the light waves and when the droplets are spaced more than one half of a wavelength apart. Light scattering, then, is what makes clouds look cloudy, scleras look white, and cataracts look gray. We will now look at the clinical examples in more detail.
NORMAL CORNEAL SCATTERING
In the normal state,1 the cornea is essentially transparent. Experiments show that the corneal stroma scatters approximately 10% of all light incident upon it.3 It is this small amount of scattering that allows us to see the corneal structures under the slit lamp.
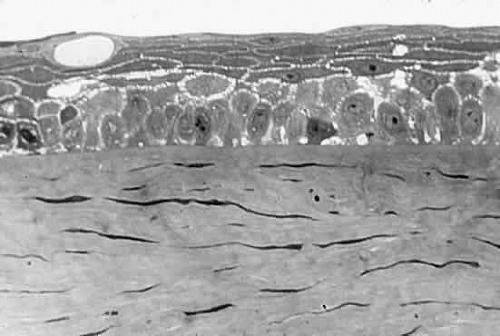
But how can the cornea be so clear if it is made of structures as diverse as epithelial cells, collagen fibers (refractive index, 1.47), and a ground substance whose refractive index is close to that of water (1.333)? The epithelial cell layer may be considered as homogeneous units of a protein solution, with each cell so tightly packed against the next that almost no extracellular water accumulates and there is virtually no fluctuation in refractive index throughout the layers. In the stroma, the collagen fibers are approximately 25 nm in diameter, and the spacing between each pair of fibrils is 60 nm. These dimensions are much smaller than a wavelength of yellow light (600 nm).4 Thus, the tiny dimensions and regular arrangement of these fibrils (Fig. 5) account for the minimal scattering.
CORNEAL STROMAL EDEMA
In cases of endothelial dystrophy, endothelial trauma, or endothelial incapacitation due to inflammation (i.e., iritis), the pumping action of the endothelium diminishes and the stroma takes on additional fluid and thickens. As interfibrillar fluid increases, the collagen fibers are pushed farther and farther apart. As the lakes of such fluid exceed one half of a wavelength of light in dimension, light scattering increases and the cornea takes on a gray appearance (see Fig. 5).4
CORNEAL EPITHELIAL EDEMA
In cases of advanced endothelial impairment or acute glaucoma, fluid collects between the epithelial cells (Fig. 6). Fluctuations in the refractive index develop, and as the spaces between the cells grow, the intensity of the scattering, or haze, grows. Potts and Friedman5 have shown that in total corneal edema, the epithelial component accounts for the greatest share of light scattering.
CORNEAL SCARS
When discontinuities in Bowman’s membrane in ulceration, trauma, or refractive surgery induces scar formation close to the pupillary center, visual acuity decreases. Scars interfere with vision in two basic ways: (1) they cause an irregularity of the corneal surface, producing irregular astigmatism; (2) stromal scars contain either randomly arranged collagen fibers, the diameters of which are five times the diameter of normal corneal fibrils, or unusual material such as hyaluronic acid, which pushes the collagen fibers far apart. This results in backscatter of light, which yields a white appearance to the observer and foggy vision to the patient.
SCATTERING IN THE NORMAL LENS
The normal lens is not as transparent as the normal cornea. This is partially caused by the faint yellow pigment, which absorbs 10% to 40% of all visible blue light. This hint of yellow is augmented by normal Rayleigh scattering, present in the healthy lens. The normal clear lens, composed of tightly packed high-protein-content lens fibers, scatters a small amount of light. With aging, however, large protein aggregates form within the lens fibers, reaching molecular weights of approximately 50 × 106 g/mol.
CATARACT
As a cataract develops, a normally uniform background of proteins is disturbed by large lumps of protein aggregates. If these large lumps are uncorrelated in position, and if the aggregates are large enough, significant scattering will produce a turbid appearance. As the protein continues to clump, fluid pools develop between lens fibers, and scattering increases further. At some point in this progression, the clinician decides to describe the patient’s lens as cataractous.
SCATTERING IN THE NORMAL VITREOUS
The vitreous, a composite of a 1% hyaluronic acid solution, is interspersed with collagen fibers of approximately 10 nm in diameter.6 These fibers are almost three times smaller than the normal corneal collagen fibers. Since the scattering from each fiber is proportional to the fourth power of the collagen diameter, we can expect the scattering per fiber to be 80 times weaker for vitreous collagen than for corneal collagen. Thus, the effect of the collagen in the vitreous is quite small, and the vitreous will scatter only 0.1% of incident light. With age, vitreous collagen fibrils coalesce, fluid pockets form, and localized scattering develops to the point where the patient notices floating specks and threads.
RETINAL SCATTERING
Because the ubiquitous Müller cells seem to squeeze tightly within the spacings between the retinal cells, the tissue is homogeneous from a refractive index standpoint and scatters about as much light as the cornea.
If, however, the blood supply to a retinal area is interrupted and infarction takes place, the area fed by the occluded vessel becomes milky gray. With infarction, edema fluid accumulates in the nerve fiber layer. Because the refractive index of edema fluid differs from that of the nerve fiber axons, the area loses transparency.
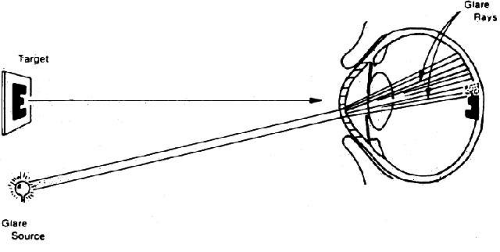
GLARE
The term “glare” is often used to describe the contrast-lowering effect of stray light on a visual scene. The outfielder is said to lose a fly ball into the sun because of glare. Extra light thrown onto the retina tends to wash out the contrast of the event we are viewing. For example, every student is aware of the importance of pulling down all the shades and darkening the room if all the details of a slide projected on a screen are to be appreciated. Because of the nature of the light-detecting mechanism at the retina and in the brain, we cannot see intensity differences efficiently in the presence of a high background of light intensity.
This sensitivity to glare is amplified as lens (or corneal) scattering is increased. For example, the older surgeon cannot see the details within a deep surgical wound in the presence of white surgical sponges.7 These sponges act as extraneous light sources, which are scattered by the aging crystalline lens onto the macula of the surgeon’s retina.8 Again, the patient with a poorly fitted contact lens who develops epithelial corneal edema reports unusual glare from automobile headlights at night. In cases of cataract or marked corneal edema, the patient has difficulty reading in a bright environment, where all the elements of normal light become sources of glare. This phenomenon is illustrated in Figure 7.
Some time ago, we wondered what percentage of a lens must actually become cataractous or, put another way, how much of the lens must remain clear before scattering and consequent glare reach levels significant enough to impair visual acuity. Although contrast started to drop slightly when almost half the lens was “covered with cataract,” contrast dropped suddenly when 80% of the lens became cataractous.9
Thus, light scattering, glare, and visual performance are all tightly bound together.
CLINICAL GLARE TESTING
In 1926, the industrial scientist L.L. Holladay10 first described the relationship between glare and contrast sensitivity. Holladay developed a mathematical relationship between the glare source (its brightness and angular distance from the target) and contrast sensitivity. In the 1960s, Ernst Wolf,8,11,12 a Boston visual physiologist, built a laboratory glare tester and showed in a normal population that glare sensitivity increased with age. He also showed that this increase in glare sensitivity was related to the increased light scattering of the normal, aging lens. In the 1970s and early 1980s, Miller, Wolf, Nadler, and others13,14 built and tested the first clinical glare tester (Miller-Nadler glare tester; Fig. 8). With this device, they demonstrated a connection between cataract progress and increased glare sensitivity.14 Figure 9 shows a plot of glare sensitivity versus visual acuity in 144 patients with cataracts. What strikes one immediately is that the visual acuity is randomly scattered throughout the plot, whereas glare sensitivity increases in an orderly progression. Glare sensitivity also correlated highly with the degree of posterior capsule opacification after extracapsular cataract extraction and intraocular lens implantation.15
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree