Lasik Outcomes in Astigmatism
Damien Gatinel
Thanh Hoang-Xuan
BACKGROUND
Compound astigmatism is the most common refractive error. Myopia is often associated with some degree of astigmatism in the general population. It is estimated that astigmatism of more than 0.50 diopters (D) is present in 44.4% of the population, and that 8.44% of these subjects have astigmatism of 1.50 D or more (1). Corneal incisions have been used to correct astigmatism for more than a century (2,3). In 1983, Trokel et al. (4) showed that smooth ablation of the cornea was feasible using a 193-nm excimer laser. In 1991, McDonnell et al. (5) used toric ablation to correct astigmatism by reshaping the anterior corneal surface. For more than a decade, excimer laser surgery has been the most predictive and safest technique to treat regular astigmatism. Currently, the most common surgical methods for correcting astigmatism are photoastigmatic refractive keratectomy (PARK) and laser in-situ keratomileusis (LASIK). LASIK provides better accuracy and higher patient satisfaction than PARK for the treatment of moderate to high astigmatism (6, 7, 8). However, in both cases the predictability of excimer laser surgery is lower for compound or pure astigmatism than for pure spherical myopic errors. This is partly due to the inherent remodeling imposed on the corneal surface by cylindrical profiles of ablation.
The profiles of ablation for conventional noncustomized treatments do not take into account the higher-order optical aberrations of the human eye. Moreover, these treatments carry a risk of increasing higher-order aberrations such as coma and spherical aberration (9). Recently, wavefront sensors were introduced to quantify the overall optical aberration of the eye. The astigmatic refractive error can be isolated from a Taylor or Zernike polynomial expansion aimed at describing the wavefront error of the total eye over a circular pupil. It arises from the effects of second radial order and azimuthal frequency terms of the Zernike classification (10). New algorithms have been introduced for laser delivery systems, with the aim of correcting both low- and high-order optical aberrations, with encouraging early results.
This chapter focuses on the different strategies used to determine the profile of ablation, and on the particularities of the LASIK technique aimed at correcting pure, compound, and mixed regular astigmatism. The treatment of irregular and/or high-order astigmatism by means of customized ablation will not be discussed in detail.
DEFINITIONS: REGULAR ASTIGMATISM, IRREGULAR ASTIGMATISM, AND HIGH-ORDER ASTIGMATISM
The astigmatic error is a refractive error dependent on the meridian. It is usually due to one or more refracting surfaces—most commonly the anterior cornea, having a toroidal shape. In regular astigmatism, the principal meridians (maximum and minimum power) are perpendicular to each other, and the astigmatism is correctable with conventional spherocylindrical lenses or surgery.
When the principal meridians are not perpendicular to each other, the astigmatism is irregular. Computerized corneal topography has made an important contribution to the diagnosis of regular and irregular anterior corneal astigmatism.
In recent years interest has grown in measuring the optical aberrations of the human eye and changes induced by refractive surgery. The optical imperfections previously designated “irregular astigmatism” can now be more precisely characterized and quantified with novel approaches such as wavefront analysis. The variance of the normalized Zernike expansion is the tool most commonly used to describe and quantify optical aberrations in terms of wave-aberration coefficients. Each Zernike mode is defined by its radial order and azimuthal frequency, and is weighted by a coefficient. These coefficients correspond to the contribution of each mode to the total root mean square (RMS) wavefront error. Some Zernike modes (trefoil, quadrafoil, pentafoil, etc.) correspond to so-called high-order astigmatism. These modes have in common that their radial
order is equal to their azimuthal frequency. Terms having an azimuthal frequency of 2 but a higher even radial order n are commonly referred to as “n-order” astigmatism. In normal patients, theory contribution to the degradation of the quality of vision is usually small relative to that induced by the conventional spherocylindrical refractive error, because of their small contribution to the total wavefront deviation. However, they may limit the vision of healthy eyes to less than retinal limits and, in some clinical circumstances (early keratoconus, corneal scarring, etc.), they may significantly affect visual acuity and overall quality of vision, especially in subjects with scotopic pupil.
order is equal to their azimuthal frequency. Terms having an azimuthal frequency of 2 but a higher even radial order n are commonly referred to as “n-order” astigmatism. In normal patients, theory contribution to the degradation of the quality of vision is usually small relative to that induced by the conventional spherocylindrical refractive error, because of their small contribution to the total wavefront deviation. However, they may limit the vision of healthy eyes to less than retinal limits and, in some clinical circumstances (early keratoconus, corneal scarring, etc.), they may significantly affect visual acuity and overall quality of vision, especially in subjects with scotopic pupil.
PRINCIPLES OF CORRECTION OF REGULAR ASTIGMATISM
Regular astigmatism is mainly generated by excessive corneal toricity. Thereby, LASIK for astigmatism is a subtractive technique aimed at reducing this excessive toricity by etching from the corneal surface an adequate toric lenticule of corneal tissue of variable thickness. Corneal toricity can be suppressed by either flattening the steepest meridians to the curvature of the initially flatter meridian, or by “steepening” the flattest meridians to the curvature of the initially steeper meridian. Pure positive and negative cylindrical excimer laser treatments are based on the combination of three elementary profiles of ablation, as depicted in Fig. 79-1 and Table 79-1.
 FIGURE 79-1. Schematic representation of the three elementary profiles of ablation used to establish the cylindrical profiles of ablation. Steepening of the meridians (A) is achieved in the pure positive cylindrical mode. Flattening (B) and plano ablation (C) are achieved in the pure negative cylindrical mode. (Artwork generated using computer-aided modeling) |
The treatment of astigmatism in LASIK requires proper alignment of the corneal surface relative to the delivery system, and smooth blending of the steep edges of variable depth induced at the periphery of the optical zone, in order to avoid undercorrection. These two major constraints may account for the high reported rate of undercorrection of the cylindrical component and overcorrection of the spherical component.
Some authors have drawn attention to the geometric particularities of astigmatic treatment, implying the need for a larger transition zone along the initially flatter meridian (11,12), minimization of the maximal depth of ablation, and comparison of different strategies for mixed and compound astigmatism (13). In a recent paper, we emphasized
the three-dimensional geometric features of the ablated lenticules of corneal tissue when correcting pure and compound astigmatism (14). We used computerized three-dimensional (3D) modeling to represent and compare the qualitative geometric characteristics of the different lenticules and ablation strategies. The surfaces of ablation were modeled as geometric primitives such as the sphere and the toroidal ellipsoid with which the Boolean operations were performed. To model the lenticules etched for pure cylindrical corrections, the initial corneal surface was modeled as a toroidal ellipsoid with two major apical radii of curvature along the principal meridians. For lenticules etched for pure spherical corrections, we modeled the initial surface as spherical. The final surface was always spherical. The principal radii of curvature of the initial and final surfaces were adjusted according to the nature of the ametropia (the radii of the initial surface being shorter for myopic lenticules and longer for hyperopic lenticules). The difference between each of the radii of curvature was exaggerated as compared to the surgical range so as to facilitate spatial visualization of the contour of the lenticules. Such an approach is useful to conceptualize the constraints of cylindrical treatments, to compare the depth and volume ablated in different strategies, and to anticipate some unpredicted effects. This approach is used in this chapter to illustrate the differences between strategies aimed at treating pure astigmatism and compound astigmatism.
the three-dimensional geometric features of the ablated lenticules of corneal tissue when correcting pure and compound astigmatism (14). We used computerized three-dimensional (3D) modeling to represent and compare the qualitative geometric characteristics of the different lenticules and ablation strategies. The surfaces of ablation were modeled as geometric primitives such as the sphere and the toroidal ellipsoid with which the Boolean operations were performed. To model the lenticules etched for pure cylindrical corrections, the initial corneal surface was modeled as a toroidal ellipsoid with two major apical radii of curvature along the principal meridians. For lenticules etched for pure spherical corrections, we modeled the initial surface as spherical. The final surface was always spherical. The principal radii of curvature of the initial and final surfaces were adjusted according to the nature of the ametropia (the radii of the initial surface being shorter for myopic lenticules and longer for hyperopic lenticules). The difference between each of the radii of curvature was exaggerated as compared to the surgical range so as to facilitate spatial visualization of the contour of the lenticules. Such an approach is useful to conceptualize the constraints of cylindrical treatments, to compare the depth and volume ablated in different strategies, and to anticipate some unpredicted effects. This approach is used in this chapter to illustrate the differences between strategies aimed at treating pure astigmatism and compound astigmatism.
TABLE 79-1. PRINCIPLES OF CORRECTION OF REGULAR ASTIGMATISM | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Simple Astigmatism
Shape of the Ablated Lenticule in Pure Cylindrical Hyperopic Treatment
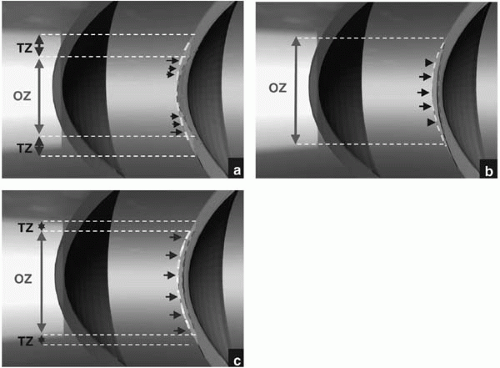
Cylindrical hyperopic ablation within the optical zone consists of ablating a lenticule with a concave shape along the initial flatter meridian, and of zero thickness along the opposite meridian, which has the same radius of curvature as the final surface (Fig. 79-2A). The maximal thickness of the cylindrical hyperopic lenticule is located at the edge of the optical zone, along the initial flatter meridian, and is identical to that of a spherical hyperopic lenticule for the same magnitude of treatment.
A transition zone is required to blend the edges of the treatment zone. To minimize the amount of tissue removed and to equalize the slope of the transition zone, the latter should be made elliptical, with maximal width along the initially flatter meridian (Fig. 79-2B) (11,12,15).
Shape of the Ablated Lenticule for Simple Myopic Astigmatism
Pure cylindrical myopic ablation consists of ablating a lenticule with a convex shape along the initial steeper meridian and with constant thickness along the initial flatter meridian, in order to preserve its curvature (Fig. 79-2C). Because of this latter constraint, the amount of the pure cylinder treatment is superior to the amount of the spherical treatment for a given degree of dioptric treatment. The maximal thickness of the myopic cylindrical ablated lenticule is located along the flatter meridian, and is identical to that of a spherical myopic lenticule for a given magnitude of treatment. This ablation pattern along the flat meridian is equivalent to that of a plano ablation, and explains the frequent unanticipated effects, from the optical and engineering perspectives, of negative cylindrical treatment, such as undercorrection and hyperopic shift (16). To minimize the intensity of these phenomena, the edges of the ablation over the optical zone have to be smoothed out evenly, by enlarging the transition along the initially flatter meridian, thus creating an elliptical perimeter for the total ablation zone (Fig. 79-2D).
Because the initially steeper principal meridian cannot be flattened selectively (this would imply plano ablation on the other principal meridian), the lenticule ablated for cylindrical myopic treatment can be considered as a combination of two successive treatments: cylindrical positive treatment of equal magnitude on the initially flatter meridian (to steepen its curvature until it equals that of the opposite principal meridian), followed by myopic spherical treatment of similar magnitude aiming to flatten both meridians (Fig. 79-3). The final surface is spherical, and its radius is equal to that of the initially flatter meridian. For example, a cylindrical treatment −1 × 180 degrees is equivalent in terms of the optical results and the amount of ablated tissue to the following sequential treatment: +1 × 90 degrees and −1. This additive relation is useful to compare strategies used to treat compound and mixed astigmatism.
Mixed and Compound Astigmatism
Sequential Strategy
Conventional strategies used to correct compound myopic astigmatism are sequential: the spherical and cylindrical components of the refractive errors are treated successively, over a circular optical zone. Noncustom PARK or LASIK ablation of pure, compound, or mixed astigmatic refractive errors is based on paraxial models first described by Munnerlyn et al. (17). They generally employ one or more of four elementary treatments, namely spherical myopic, spherical hyperopic, cylindrical myopic, and cylindrical hyperopic. Thus, to achieve emmetropia, tissue photoablation within the optical zone must yield a single final apical corneal curvature. As refraction (as commonly measured in
clinical practice) is an arc-based mathematical expression limited to the principal major and minor axes, a compound astigmatic refractive error can be expressed by different equivalent expressions. Thus, various sequential treatment strategies for the correction of compound astigmatism have been proposed, consisting of a combination of spherical and cylindrical treatments, as follows:
clinical practice) is an arc-based mathematical expression limited to the principal major and minor axes, a compound astigmatic refractive error can be expressed by different equivalent expressions. Thus, various sequential treatment strategies for the correction of compound astigmatism have been proposed, consisting of a combination of spherical and cylindrical treatments, as follows:
 FIGURE 79-2. Schematic representation using three-dimensional computer modeling (Boolean operations) of the ablated lenticules etched for the positive cylinder treatment (A,B) and for the negative cylinder treatment (C,D). The profile of ablation has been outlined over different meridians of the lenticules (A,C) (optical zone only). B,D, A lenticule corresponding to the tissue ablated for the realization of a transition zone of constant slope is added wherever an abrupt step is sculpted in the cornea at the outer perimeter of the optical zone. In both the negative and positive cylinder treatments, the peripheral depth is maximum along the initial flat meridian (FM), and is null along the initial steep meridian (SM). The transition zone is thus elliptical, having its widest diameter along the initial flatter meridian. (Artwork generated using computer-aided modeling) |
Ablating the cylinder along the flattest meridian, and then treating the residual spherical component (positive cylinder approach);
Ablating the cylinder along the steepest meridian, and then treating the residual spherical component (negative cylinder approach);
Ablating the total refractive error by two pure cylindrical ablations of opposite signs along the principal meridians (bitoric approach); and
Ablating half the power of the cylinder along the steepest meridian, and the remaining half along the flattest meridian, before treating the residual spherical equivalent (cross cylinder approach).
These strategies have been employed to treat compound myopic, compound hyperopic and mixed astigmatism. Azar and Primack (13) have illustrated the use of these strategies in mixed and compound hyperopic astigmatism, and have shown that they may result in different amounts and depths of corneal tissue ablation. They found that
strategies combining hyperopic spherical and myopic cylindrical corrections incur the greatest amount of corneal tissue ablation. The increasing number of reports of corneal ectasia following LASIK (18, 19, 20, 21, 22, 23) suggests that strategies that remove the least corneal tissue should be preferred for the treatment of compound and mixed astigmatism. Azar et al. compared the theoretical ablation profiles and depths of tissue removal in the treatment of compound hyperopic astigmatism and mixed astigmatism, but did not offer a direct estimate of the difference in the amount of tissue ablation. Using Boolean operations, we designed a method to compare and illustrate the amount of tissue ablation incurred by different sequential strategies (14). This method confirmed the universal utility of combining plus cylindrical and negative or positive spherical ablations when treating any compound or mixed astigmatism while theoretically minimizing the volume of ablated corneal tissue (Figs. 79-4 and 79-5). Using this approach, the magnitude of astigmatism to correct is expressed in the positive cylinder format of the refraction. It implies variable steepening of the corneal surface, aimed at reducing or suppressing the toricity of the anterior corneal surface, followed by a pure positive or negative spherical treatment to correct for the remaining defocus.
strategies combining hyperopic spherical and myopic cylindrical corrections incur the greatest amount of corneal tissue ablation. The increasing number of reports of corneal ectasia following LASIK (18, 19, 20, 21, 22, 23) suggests that strategies that remove the least corneal tissue should be preferred for the treatment of compound and mixed astigmatism. Azar et al. compared the theoretical ablation profiles and depths of tissue removal in the treatment of compound hyperopic astigmatism and mixed astigmatism, but did not offer a direct estimate of the difference in the amount of tissue ablation. Using Boolean operations, we designed a method to compare and illustrate the amount of tissue ablation incurred by different sequential strategies (14). This method confirmed the universal utility of combining plus cylindrical and negative or positive spherical ablations when treating any compound or mixed astigmatism while theoretically minimizing the volume of ablated corneal tissue (Figs. 79-4 and 79-5). Using this approach, the magnitude of astigmatism to correct is expressed in the positive cylinder format of the refraction. It implies variable steepening of the corneal surface, aimed at reducing or suppressing the toricity of the anterior corneal surface, followed by a pure positive or negative spherical treatment to correct for the remaining defocus.
 FIGURE 79-3. Decomposition of the lenticule corresponding to the volume ablated for the negative cylinder (NC) treatment into two lenticules, corresponding to the volume of a negative spherical and positive cylindrical volumes, respectively. For example, the negative cylinder treatment (−2 × 0 degrees) results in the same amount of ablated tissue that the following sequence: (−2 sphere) and (+2 × 90 degrees). (Artwork generated using computer-aided modeling) |
Negative cylindrical approaches to compound hyperopic or mixed astigmatism result in additional tissue ablation, the amount of which results from the combination of the myopic spherical treatment in the flat meridian (which is part of the negative-cylindrical treatment) with a positivespherical lenticule (in both meridians). This combination also occurs with the cross-cylindrical ablation strategy when it is used to correct mixed or compound hyperopic astigmatism. This strategy has been proposed to favor postoperative prolate asphericity and to reduce the overcorrection on nonprincipal meridians (24,25). In hyperopic astigmatism, the cross-cylinder technique may also reduce the increase in corneal eccentricity, leading to a more physiologic corneal shape (26).
For mixed astigmatism, the positive-cylindrical approach and bitoric ablation would theoretically incur the same minimum volume of tissue ablation. However, because of the global characteristics of the cylindrical profiles of ablation achieved with the newest delivery systems (wide elliptical transition zones), a bitoric strategy might be more practical to treat mixed astigmatism (27). The bitoric strategy has also been shown to reduce the hyperopic shift caused by the use of the negative cylindrical treatment, by ablating more selectively along the extremities of the flat
meridian (positive cylindrical treatment), thus preventing the flattening of the latter and avoiding a shift of refraction toward hyperopia.
meridian (positive cylindrical treatment), thus preventing the flattening of the latter and avoiding a shift of refraction toward hyperopia.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
