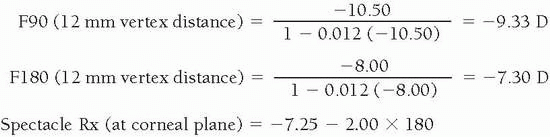
List the spectacle correction (Rx) and keratometric readings.
The effective power should be determined at the corneal plane (if indicated).
Determine the lacrimal lens power induced by the base curve radius (BCR) of the lens.
Add together the powers of the contact lens, lacrimal lens, and the difference between the keratometric readings of the principal corneal meridians.
With the following formula, subtract the value obtained in step 4 from the spectacle correction to obtain the overrefraction:
Overrefraction (OR) = Spectacle Rx − [Contact Lens Power (CLP) + Lacrimal Lens Power (LLP) + ΔK]
1. | Spectacle Rx | = − 2.00 − 2.50 × 180 |
Keratometry | = 43.00 @ 180; 45.00 @ 090 | |
Diagnostic lens | = −3.00 D; 43.25 D base curve radius | |
2. | At corneal plane, spectacle Rx | = −2.00 − 2.25 × 180 |
3. | LLP | = 43.25 − 43.00 = +0.25 |
4. | CLP + LLP + ΔK | = LLP + ΔK = [−3.00 + (+)0.25] + (−)2.00 × 180 |
= −2.75 − 2.00 × 180 | ||
5. | OR | = Spectacle Rx − (CLP + LLP + ΔK) |
= −2.00 − 2.25 × 180 − (−2.75 −2.00 × 180) | ||
= +0.75 − 0.25 × 180 |
equations are necessary to determine the CRA. Because of the time involved, unless the appropriate tables or a computer-assisted contact lens design program is available, the use of a GP, spherical diagnostic lens for overrefraction to determine the residual astigmatism is advisable.
a spherical soft lens should provide acceptable visual acuity. This is demonstrated in Example 8.
Most soft toric lenses are available in these parameters; higher-cylinder-power custom lenses are available at slightly more—to much greater—expense.
Most diagnostic sets and inventories are in these parameters.
In high refractive astigmatism, rotation of the lens with the blink may reduce visual acuity.
Oblique cylinder axes tend to result in greater lid effect on the lens edge; therefore, rotational instability is possible.
Trial frame. The patient can also wear a trial frame in combination with a low-power cylinder trial lens having hash marks for judgement of rotation (Fig. 14.1). The marks on the spectacle trial lens can be aligned with both the prism base and the optical section beam, and the degree reading can be read directly from the trial frame.
Slit-lamp beam rotation. Many of the slit lamps in use today allow the practitioner to rotate the optical section to align with the position of the prism base. The amount of rotation can be read directly from a scale on the slit lamp.
“Guesstimate.” The most commonly used (and convenient) method is simply to estimate the amount of rotation with the blink. Because it is very easy to underestimate the amount of rotation, always think of the lens as a clock, with each hour equivalent to 30 degrees. If the prism base appears to be at approximately 6:30 (not 6 o’clock), the prism base has rotated 15 degrees. The importance of proper evaluation of rotational amount and stability is discussed further in the section of this chapter on soft toric lenses.
OD | OS | |
|---|---|---|
LLP | = Spectacle Rx − (CLP + OR) | |
= [−1.50 − 1.00 × 090] − | [−2.50 − 1.25 × 090] | |
[(−3.00) + (+) 1.25 − 1.50 | − [(−3.00) + (+)0.25 − 1.00 | |
× 090] | × 090] | |
= [−1.50 − 1.00 × 090] | [−2.50 − 1.25 × 090] | |
− [(−)1.75 − 1.50 × 090] | − [(−)2.75 − 1.00 × 090] | |
= +0.25 + 0.50 × 090 | +0.25 − 0.25 + 090 |
OD | OS | |
|---|---|---|
CLP | = Spectacle Rx − LLP | |
= [−1.50 − 1.00 × 090] | [−2.50 − 1.25 × 090] | |
= [+0.25 + 0.50 × 090] | − (+)0.25 − 0.25 × 090 | |
= −1.75 − 1.50 × 090 | −2.75 − 1.00 × 090 |
OD | OS |
|---|---|
−3.25 + 1.50 × 180 | −3.75 + 1.00 × 180 |
OD | OS |
|---|---|
−3.25 + 1.50 × 165 | −3.75 + 1.00 × 015 |
Parameter | OD | OS |
|---|---|---|
BCR | 43.50 (7.76) | 43.50 (7.76) |
CLP | −3.25 + 1.50 × 165 | −3.75 + 1.00 × 015 |
OAD | 9.0 | 9.0 |
OZD | 7.8 | 7.8 |
SCR/W (=BCR + 1 mm) | 8.8/.3 | 8.8/.3 |
PCR/W (=SCR + 2 mm) | 10.8/.3 | 10.8/.3 |
CT | 0.26 | 0.25 |
Prism | 1Δ, double dot base | 1Δ, dot base |
Material | Fluoroperm 60 | Fluoroperm 60 |
Add. information | Minus carrier | Minus carrier |
Parameter | OD | OS |
|---|---|---|
Base curve radius | 43.50 (7.76) | 43.50 (7.76) |
CLP | −3.25 + 1.50 × 165 | −3.75 + 1.00 × 015 |
OAD | 9.4/8.9 | 9.4/8.9 |
OZD | 7.8 (decentered 0.5 mm) up | 7.8 (same as OD) |
SCR/W | 8.8/0.3 | 8.8/0.3 |
PCR/W | 10.8/0.3 | 10.8/0.3 |
CT | 0.26 | 0.25 |
Prism | 1.25 Δ | 1.25 Δ |
Material | Fluoroperm 60 | Fluoroperm 60 |
Add. information | Double dot base | Dot base |
Truncation 15° temp OU |
Vision is blurred.
Discomfort results from prism, truncation, or both.
Quality control is poor.
4. Inferior decentration causes flare and possibly corneal desiccation.
It is not possible to modify the front surface.
If unilateral, asthenopia can result from a vertical imbalance although low amounts of prism (i.e., 0.75 − 1 Δ) can usually be tolerated.
Edema can develop if a low-Dk GP lens material is used.
meridian. The cylinder power of the lens is the same on the eye as in air when measured with the lensometer, as the cylinder is on the front surface only. If the lens was ordered with the power −3.25 +1.25 × 075, this should be the power read with the lensometer.
TABLE 14.1 CIRCULAR PRISM-BALLASTED TRIAL LENS SET (10 LENSES) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
numerous companies manufacture custom soft toric lenses in practically any axis and power, and improvements in edge designs have resulted in better subjective comfort than was attained with previous-generation designs. Finally, computer-assisted lens design programs are available that are especially beneficial in cross-cylinder situations and currently are being used by both practitioners and manufacturers.15 This type of program is capable of providing a recommended cylinder axis and power based on the patient’s refractive data, the diagnostic lens parameters, and the amount of rotation on the eye.
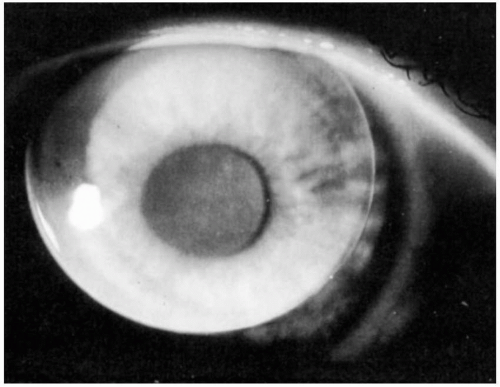 ▪ FIGURE 14.3 An aspheric lens (Boston Envision) providing good centration and a less obvious “dumbbell-shaped” fluorescein pattern than present with a spherical design. |
Secondary curve radii (SCR) = 1.0 mm flatter than the base curve radii [e.g., if the base curve radii are 41 D (8.23 mm) and 44 D (7.67 mm), the SCR would be 9.23/8.67 mm or rounded off to 9.2/8.7 mm].
Peripheral curve radii (PCR) = 3.0 mm flatter than the BCRs; in the above case they would be equal to 11.2/10.7 mm.
TABLE 14.2 MANDELL-MOORE FIT FACTOR | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||
Kf = 40.50 + (−)0.25 = 40.25 D
Ks = 44.50 − 0.75 = 43.75 D
Ff = +0.50 + (0.25)(LLP) = +0.75 D
Fs = +0.75 + (40.25 − 43.75) = −2.75 D
BCR | Power | SCR/W | PCR/W | OAD |
|---|---|---|---|---|
40.25/43.75 | +0.75 | 9.00/.3 | 11.00/.3 | 9.2 |
(8.38)(7.71) |
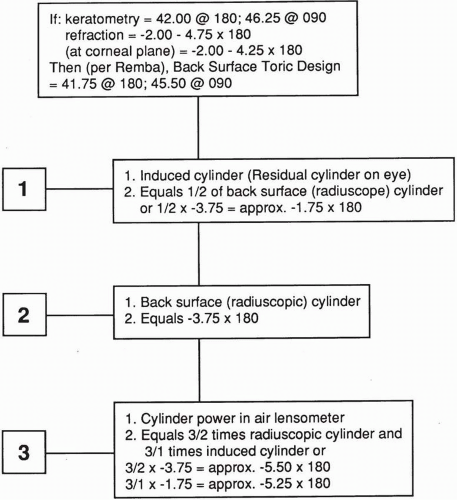
From back surface lens toricity (measured with the radiuscope) to contact lens cylinder power in air (measured with the lensometer)—multiply by 1.452 (or approximately 1.5).
From back surface lens toricity (measured with the radiuscope) to the contact lens cylinder power measured in fluid (on the eye or induced)—multiply by 0.456 (or approximately one-half).
From contact lens cylinder power in air (measured with the lensometer) to the contact lens cylinder power in fluid (on the eye or induced)—multiply by 0.314 (or approximately one-third).
From the contact lens cylinder power in fluid (on the eye or induced) to the contact lens cylinder power in air (measured with the lensometer)—multiply by 3.19 (or approximately 3).
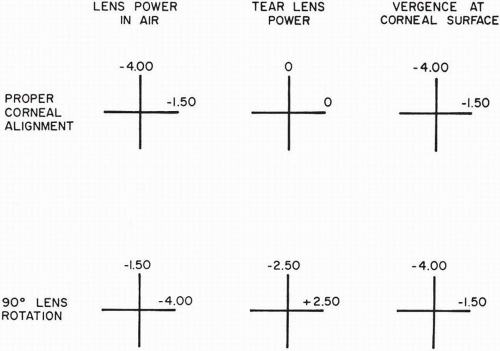
the corneal toricity is against-the-rule and the residual astigmatism is approximately 0.5 times the amount of back surface toricity of the lens (as measured with the radiuscope).
shown in Figure 14.6 in which the extreme case of 90-degree rotation is provided. It is shown that the tear layer will compensate, and the front surface cylinder correction will still equal the new cylinder and axis of the induced cylinder.
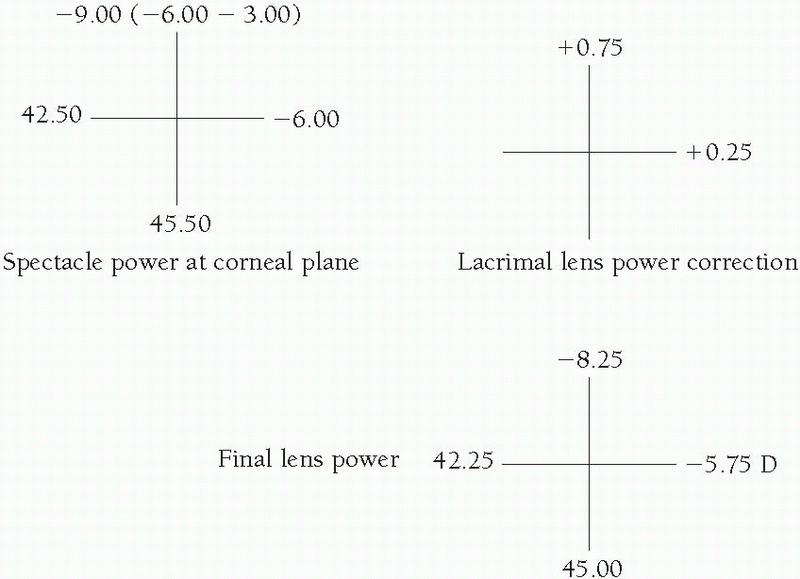
Perform a spherical refraction over the selected SPE diagnostic lens.
Add the overrefraction to the powers in the flat and steep meridians of the diagnostic lens.
Select the recommended SPE diagnostic lens.
Perform a spherical overrefraction; if the visual acuity is reduced, perform a spherocylindrical overrefraction.
Use Silbert’s rule8 to determine the final lens powers: “If the axes are at or near the principal corneal meridians, add the appropriate power in the refraction to the air power of the corresponding meridian in the diagnostic lens, and order.”