Correction of Ametropia with Spectacle Lenses
Susannah B. Marcus
Melvin L. Rubin
The provision of spectacles to correct vision is based on both science and art. Prescribing appropriate corrective lenses depends on the ability of the patient to adapt to change and the patient-specific relationship between accommodation and vergence. But first and foremost, a thorough understanding of the optical principles of lenses and of the eye is necessary. Armed with that knowledge and supplemented by clinical experience, you can attain true competency in providing optimal visual correction for each of your patients.
OPTICAL PRINCIPLES
OBJECT/IMAGE CONJUGACY IN AMETROPIC EYES
An object and the image of that object created by any optical system are said to be conjugate to one another. That is, the positions of the object and its image could trade places if the light rays were reversed. (This principal of object–image interchangeability evokes the ancient concept of the “visual spirit,” which was regarded as a vital force emanating from the eye of an observer to create visual perception.)
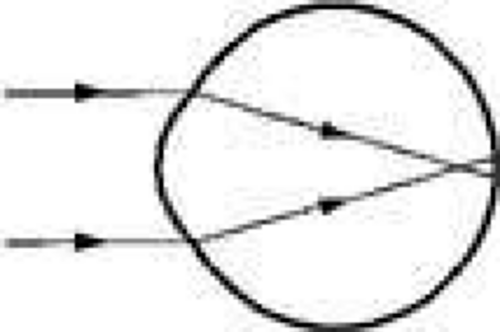
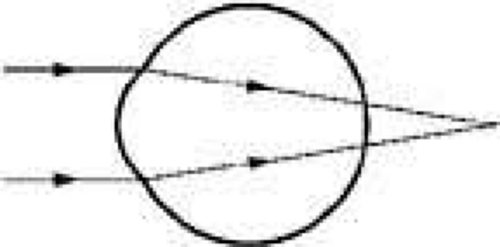
In a nonaccommodating emmetropic eye, a distant object is conjugate to the retina (Fig. 1); that is, a distant object is crisply imaged on the retina. Conversely, if the retina were the object, its image would be located at an infinite distance in front of it. If the eyes’ optical elements do not create conjugacy between the retina and a distant object, ametropia exists. In the myopic eye, the sharply focused image of a distant object is not on the retina but located in front of it (Fig. 2). This occurs when the optical power is too strong relative to the existing axial length. This can happen either when the optical power of the eye is too great, the axial length is too long, or some combination of both factors. On the other hand, when an eye is hyperopic, light rays from a distant object strike the retina before they have converged to form a sharp image, and this can occur because the eye has insufficient optical power, a shorter than optimal axial length, or both (Fig. 3).
 Fig. 1 In emmetropia, light rays coming from infinity are brought to focus on the retina. |
 Fig. 2 In myopia, the optical power of the eye is too strong relative to its axial length. |
 Fig. 3 In hyperopia, the optical power of the eye is too weak relative to its axial length. |
Far Point and Optical Corrections
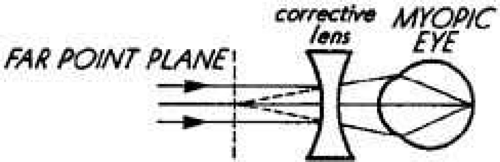
If the retina of an eye is thought of as an object, the image of the retina created by the eye’s optical system will be located at the far point plane.1 The far point denotes the location at which the far point plane intersects the optical axis. That point is conjugate to the fovea of any nonaccommodating eye. In the emmetropic eye, the far point plane is located at optical infinity (beyond 6 meters). In the myopic eye, the far point plane is located not at infinity but somewhere in front of the eye. The higher the degree of myopia, the closer the far point is to the eye. The position of the far point plane relative to the eye, actually the reciprocal of its distance in meters from the cornea, indicates the exact amount of refractive error in diopters. In the hyperopic eye, the far point plane is virtual; that is, it is located behind the eye.
The far point forms the basis for optical correction of any ametropia. Why that is so requires another important optical principle: Any lens brings light from an object located at a distance and images it at that lens’ secondary focal plane. Therefore, if that lens is positioned in front of the eye so that its secondary focal plane is superimposed on the eye’s far point plane, that lens becomes a “corrective lens.” The lens creates a focused image of a distant object and puts it at the far point plane. That image then becomes the object for the eye’s optical elements, which take over and bring a sharply focused image onto the retina (Fig. 4).
 Fig. 4 Far point plane in myopia is in front of the eye. A lens is corrective if its anterior focal point coincides with the far point plane. |
Lens Effectivity
Almost any lens can become a corrective lens if its secondary focal plane is placed to coincide with the ametropic eye’s far point plane. In other words, lenses of different powers may accomplish the same goal of providing sharply focused retinal images as long as this optical condition exists. All such lenses are said to have equal optical effectivity for distant objects. In fact, lenses that focus light from an object to the same point or plane are said to have equal effectivity (Fig. 5). This is an important principle because corrective spectacle lenses may be fit at different distances from the eye (or in the case of contact lenses, directly on the cornea) if their powers are appropriately adjusted. The distance between the posterior surface of a corrective lens and the anterior surface of the cornea is known as the vertex distance (Fig. 6). The effective power of a low-powered corrective lens will not vary significantly with small changes in vertex distance; however, the proper corrective power of high-powered lenses, such as those needed for high myopes, is very dependent on the lens’ distance from the eye. In this latter situation, you need to specify both the corrective power and the vertex distance if proper retinal focus is to be attained.
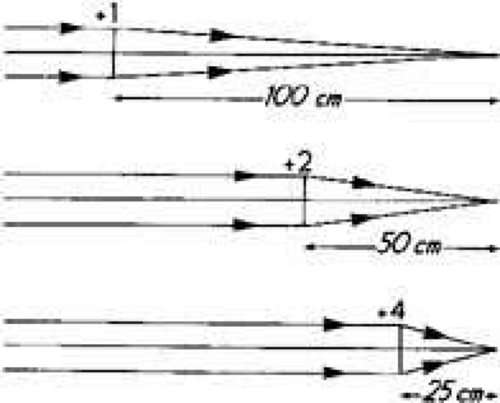 Fig. 5 Lenses of +1.00, +2.00, and +4.00D positioned to bring parallel rays of light to focal points in the same plane. These lenses are said to have the same effectivity. |
 Fig. 6 Vertex distance (V.D.) is the distance between the anterior surface of the cornea and the back surface of the eyeglass or trial lens. |
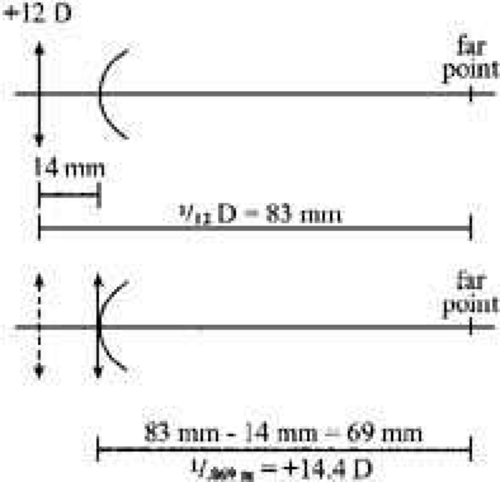
Example of prescribing a high-powered lens:
An aphakic patient’s right eye is refracted at a vertex distance of 14 mm and found to be +12.00D. What power contact lens would provide the same optical correction (i.e., the same effectivity) (Fig. 7)?
 Fig. 7 Contact lens versus spectacle corrected hyperopia. |
Both the +12.00D spectacle lens placed 14 mm in front of they eye and the +14.50D contact lens placed on the cornea will “correct” this eye because both lenses have their focal points coincident with the eye’s far point. Again, both lenses will have the same optical effectivity (though the +12 lens will produce a larger retinal image).
Effect of Changing Lens Position
If a given corrective lens is moved along the visual axis, its effectivity is changed; the image of a distant object created by the lens will no longer be coincident with the far point, which is fixed in position relative to the eye and so will result in blurring the retinal image. An optician who fits spectacles at a vertex distance different from that prescribed by the refracting clinician must appropriately alter the power of the lenses to maintain equal effectivity. Alternatively, patients whose refraction shifts over time may find that pulling their old glasses further down their noses or pushing them closer to their eyes may improve visual clarity. What they are actually doing is positioning the lenses’ secondary focal point closer to the new position of the eyes’ shifted far point. This indicates the need for a new prescription. As an example, if a patient’s myopia has gradually increased, as might occur with developing nuclear sclerosis, the eye’s previous far point will have moved closer. The now undercorrected myope will find that pushing her glasses closer to her eyes will bring the lens’ secondary focal point closer and coincident with the new far point position, and this will improve her distance visual acuity. An undercorrected hyperope will find that moving the glasses farther from his eyes will provide similar improvement.
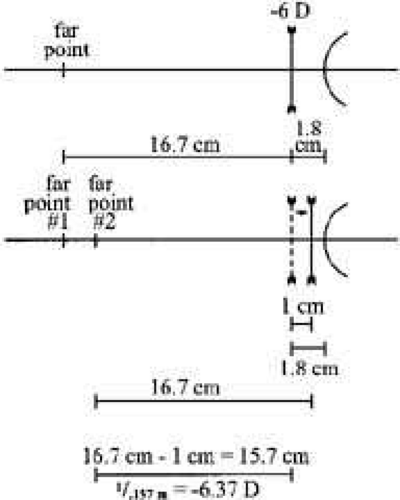
Example of how a change in spectacle vertex distance can compensate for a refractive change:
A patient who has been wearing -6.00D eyeglasses finds that, in order to see clearly, he must push his eyeglasses 1 cm closer to his eyes. What is his new refractive correction if he wants to use his current frame?
As illustrated in the diagram (Fig. 8), moving the lens closer to the eye has also moved its secondary focal point closer to the eye, making it coincident with the new far point of the eye. A -6.37D lens located at the initial vertex distance would allow correction of this new ametropia without having to adjust the position of the original frame and lens position. The patient has become 0.37D more myopic.
 Fig. 8 Vertex distance alteration may compensate for a change in refractive error. |
CORRECTION OF MYOPIA
Basic Optics
As previously mentioned, the far point plane of the myopic eye is located at a certain distance in front of the eye and determines the degree of myopia. The greater the myopia, the closer the far point will be. A real object placed at that distance (far point plane) will be in sharp focus on the retina. Thus, an uncorrected myope can hold an object at the eye’s far point plane and see it clearly. The term nearsighted is an accurate description of the myope’s visual condition. By measuring the distance at which a nonaccommodating myope holds reading material, one can make a good estimation of the degree of myopia present. For example, if a presbyopic patient holds reading material at 20 cm, he is likely to be a 5D myope.
For the myope, all objects located further away than the far point plane will result in blurred retinal imagery. The far point plane for even low degrees of myopia will be relatively near to the patient; 1 meter away for 1D of myopia, 4 meters away for only 0.25D of myopia. This accounts for the difficulty even “low” myopes have in recognizing a friend’s face from across the street. To be seen really clearly, the friend must be no further away than the far point plane.
By definition, the lens that corrects a given degree of myopia images an object at the far point plane of the eye. A “minus” lens, a lens that diverges light, is necessary to accomplish this task. From objects at a distance, parallel light rays traveling from left to right will encounter the minus lens, the light rays will be diverged, and a virtual image will be formed to the left of the lens, at the lens’ secondary focal point. When that point is located at the far point plane of the eye, that minus lens will “correct” the myopia (refer back to Fig. 4). Again, minus lenses of different powers can correct this eye as long as each is placed at the necessary vertex distance to keep its secondary focal point precisely positioned at the eye’s far point plane. Each will have the same optical effectivity, and therefore, any of them may be used to correct this myopic eye. The closer to the eye the corrective lens is placed, the less divergence power it needs to allow its secondary focal plane to be coincident with the eye’s far point plane, therefore necessitating a weaker minus corrective lens. Obviously, a contact lens will not need to be as strong as the corresponding spectacle lens to correct the same degree of myopia. Because of the small difference in power induced by changes in vertex distance in low refractive errors, it is not typically necessary to make corresponding prescriptive changes unless the myopia is 4D or greater.
Full Versus Partial Correction of Myopia
To create a truly clear retinal image of a distant object, the full extent of myopia must be corrected. However, several issues need to be considered. First, the length of the examination room is significantly shorter than infinity. So, when refractions are performed without cycloplegia, a slight undercorrection of the full myopia may result, but this is typically no more than 0.25D. This 0.25D discrepancy may be irrelevant, but it depends on the individual’s tolerance for blur and his or her visual requirements. Usually for myopes, prescribing the actual refractive findings will be sufficient to improve vision satisfactorily.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
