Corneal Topography
Eef van der Worp
John de Brabander
Frans Jongsma
▪ INTRODUCTION
Contact lens practitioners have a high interest in the shape of the cornea. When this shape is known, a contact lens that will optimize the cornea-lens relationship can be selected, fitted, or designed. Generally, mimicking the shape of the cornea promotes comfort of lens wear and reduces mechanical effects of the lens on the cornea.
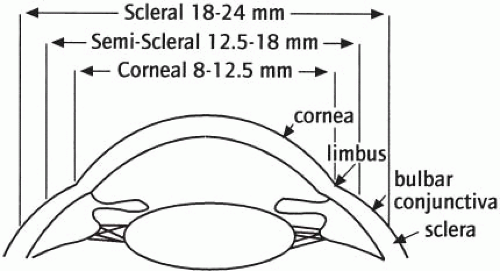
The standard procedure in contact lens practice is to measure the cornea with a keratometer. But what exactly does keratometry tell us? It typically measures the average curve of the central 3 mm of the cornea in two meridians. This includes, at minimum, three limitations. First, a keratometer measures curves and curves are not the equivalent of shape. Second, it estimates, rather than measures, the average central curves. This means it does not provide information about the exact central point (not to mention the top) of the cornea. Third, and most important: 3 mm is a very small area of a cornea. A typical cornea is 11 to 12 mm in diameter. Contact lenses, in general, cover a much larger part of the cornea than 3 mm (Fig. 3.1), and a keratometer does not provide information about the periphery of the cornea.
Corneal topography also has its limitations, all of which will be discussed in this chapter. However, when compared to the keratometer, it provides the practitioner with much more information about the geometry of the cornea and therefore can aid in optimizing the lens-tocornea fitting relationship.
Interestingly, the principle of corneal topography is as old as that of keratometry, dating back to the late 19th century. Is it impossible to measure corneal shape with a keratometer? Theoretically, peripheral curve radii can be measured by performing keratometry over the lenses and having the subject view at an angle of 25 or 30 degrees nasally, temporally, superiorly, and inferiorly. If this information is related to the central curves of the cornea, some idea about the amount of flattening toward the periphery can be obtained. Apart from the fact that with a keratometer it is often challenging to obtain reliable peripheral curve data from the periphery of the cornea, computation of corneal shape from this data is difficult.
Overall, keratometry is not the best method to measure corneal shape, apart from being time consuming. Corneal topographers can provide information about thousands of data points on the cornea that will result in a better understanding about corneal shape. More and more, practitioners will have to rely on corneal shape data rather than corneal curves. This is crucial when managing refractive surgery, orthokeratology, and keratoconus patients, but also, for the design and manufacturing of any type of contact lens, information about the shape of the cornea is essential.
In this chapter history, principles, and recently developed devices to measure the shape of the eye front surface are discussed. The primary goal is to explain how corneal topographers work, and how these devices can be used optimally in the contact lens practice.
History
For centuries ophthalmologists, optometrists, and others involved in eye care have been using the reflection capacity of the first refractive surface of the eye to obtain a qualitative impression
of the integrity of the cornea. Historically it has been described to diagnose the integrity of the cornea by viewing the reflected image of a rectangle window (Fig. 3.2). This simple diagnostic tool is based on the fact that the boundary air-tear film acts as a mirror.
of the integrity of the cornea. Historically it has been described to diagnose the integrity of the cornea by viewing the reflected image of a rectangle window (Fig. 3.2). This simple diagnostic tool is based on the fact that the boundary air-tear film acts as a mirror.
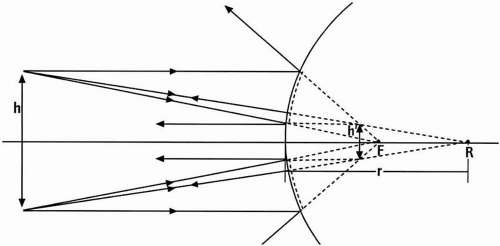
From this the basis for quantitative corneal topography was described by von Helmholtz, Placido, and Gullstrand in the late 19th century. Von Helmholtz1 measured the local slope of the cornea by observing the reflection of a pair of objects positioned at a known place with respect to the subject’s eye (Fig. 3.3). The virtual image obtained this way is called the first Purkinje image. On the basis that the cornea can be considered as an optical equivalent to a spherical mirror, Javal2 designed an instrument in which the objects could be rotated around the optical axis. In this way it became possible to find the orientation of the flattest and steepest radius of curvature, so-called “principle meridians” of the cornea. With his device more precise measurements of the cornea were introduced. Although Javal called it ophthalmometry, this technique is known today as keratometry (from keratos, Greek for cornea).
Instead of pairs of objects, Placido3 used a disk with concentric rings with a central hole through which he observed the image reflected by the subject’s eye (Fig. 3.4).
This extended the observation to more meridians, and it evaluates an entire region rather than two or more points on the cornea. With this simple but ingenious invention (also called keratoscopy), the practitioner is able to make a qualitative diagnosis of corneal irregularities and, very importantly, to estimate the amount and direction of corneal astigmatism.
Gullstrand4 took a major step in quantification of corneal topography by placing a photographic camera in the central hole of the Placido disk (Fig. 3.5). Measuring the size of the rings on the photographs enabled Gullstrand to estimate the corneal radius of curvature quantitatively. The technique, no longer in use today, was referred to as photokeratoscopy.
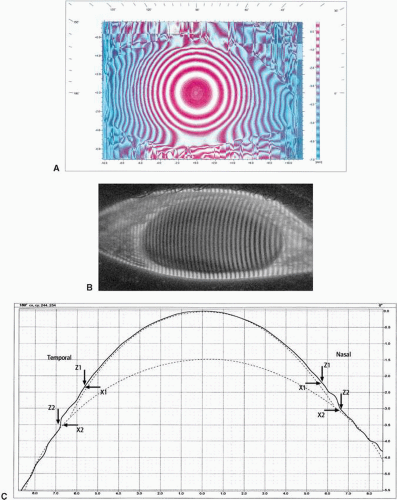
Placido disk photographs from an irregular cornea (Fig. 3.6A) and a cornea with a very steep apex, a flat superior area, and a steep inferior area, all associated with keratoconus (Fig. 3.6B), are shown. It can be observed that only a very small area of the cornea can be imaged and other areas cannot typically be interpreted or only with severe error.
A century after the invention of photography, the first television was developed, leading to the small and inexpensive charge coupled device (CCD) television systems that are common today. The modern personal computer has had a comparable history. Coupling these two devices has made it possible to collect and process a quarter of a million data points in a very brief time. After the development of algorithms for surface reconstruction, a translation of the acquired image into clinically relevant data in the 1980s, called computer-assisted video keratoscopy, was born.5
Today, these systems are simply called corneal topographers and many devices exist, but most of them are still based on the old Placido disk principle. The inherent limitations of imaging by specular reflection (see section Using a Corneal Topographer later in this chapter)
resulted in the development of alternatives. These topographic devices, based on different principles, opened new possibilities but also introduced other limitations. This has resulted in a somewhat confusing situation where it is not always possible for the practitioner to link modalities of a given device to what is desired and/or practical. This also accounts for the way image data are transformed into data of eye shape and even more how this is presented in numbers, indices, or color-coded maps.
resulted in the development of alternatives. These topographic devices, based on different principles, opened new possibilities but also introduced other limitations. This has resulted in a somewhat confusing situation where it is not always possible for the practitioner to link modalities of a given device to what is desired and/or practical. This also accounts for the way image data are transformed into data of eye shape and even more how this is presented in numbers, indices, or color-coded maps.
Corneal topography has led to the publication of a vast number of papers and patents. In a study at the University of Maastricht by Jongsma et al.6 information was found on 24 devices that were based on essentially different principles. Analyzing the principles of these devices
revealed that all devices would fit into a system that discriminates between the combinations of used light sources and the way they interact with the eye front surface (light-matter interaction). The literature descriptions yielded 12 modalities. The light source may be a lightemitting object (e.g., a Placido disk) or a projected image (e.g., a slit, lines, or a grid). The light used can be incoherent or coherent. The light matter interaction can be specular reflection, scattering, diffuse reflection, total reflection, or a combination. Not all combinations of these are technically feasible. Some are possible but rather expensive, or very difficult to use in clinical settings. Most widely used are devices based on reflection from a light-emitting object, such as the keratometer and the keratoscopes. Devices based on projection [e.g., a scanning slit or optical coherent tomography (OCT)] have entered the market recently. Generally, these devices are found to be most prevalent in ophthalmology clinics.
revealed that all devices would fit into a system that discriminates between the combinations of used light sources and the way they interact with the eye front surface (light-matter interaction). The literature descriptions yielded 12 modalities. The light source may be a lightemitting object (e.g., a Placido disk) or a projected image (e.g., a slit, lines, or a grid). The light used can be incoherent or coherent. The light matter interaction can be specular reflection, scattering, diffuse reflection, total reflection, or a combination. Not all combinations of these are technically feasible. Some are possible but rather expensive, or very difficult to use in clinical settings. Most widely used are devices based on reflection from a light-emitting object, such as the keratometer and the keratoscopes. Devices based on projection [e.g., a scanning slit or optical coherent tomography (OCT)] have entered the market recently. Generally, these devices are found to be most prevalent in ophthalmology clinics.
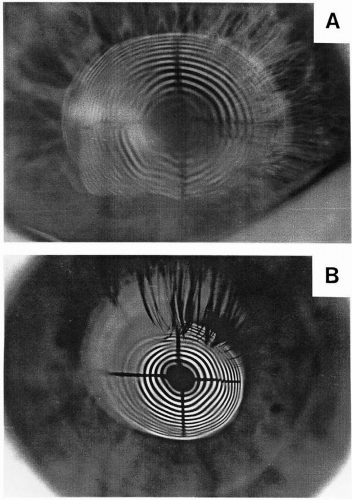 ▪ FIGURE 3.6 Placido disk photograph from an irregular cornea (A) and a cornea with a very steep apex, a flat superior part, and a steep inferior part (B, keratoconus). |
There are numerous new developments in the field of reflection corneal topographers, which will improve the accuracy and usefulness of the procedure. Collins et al.7,8 in Brisbane, Australia, for example, researched dynamic corneal topography, via which multiple topography maps can be made within seconds, creating an almost live movie of the corneal topography showing its dynamic rather than static nature. Researchers in Amsterdam, the Netherlands, developed a modified Placido disk system using different colors.9 They claim this system gives a more accurate representation about the periphery of the cornea.
In addition to this, corneal topographers are now integrated with wavefront aberrometers, which can be a major advantage in contact lens practice. Subtracting the anterior surface aberrations from the total aberrations will reveal the rest aberrations of the eye. Corneal topography then can be useful (see later section in this chapter) to aid in fitting contact lenses, and rest aberrations can be corrected on the front surface of the lens.10
Keratometry
In keratometry, the reflected image of small light-emitting targets, usually called mires, formed by the anterior surface of the cornea is used to determine the outer radius for one meridian (Fig. 3.3). By rotating the instrument about its optical axis, the principal meridians of the cornea (flattest and steepest) can be found. Actually, in keratometry it is not the size of an object that is compared with a formed image—the separation between the two mires at the object plane is compared with the measured separation in the image. To exactly measure the latter separation, keratometers have a built-in doubling system. As can be observed from Figure 3.3, only a very small area of the cornea is used to reflect the two mires. The angle between the incoming ray from the mires and the reflected ray from the cornea, called the collimator angle, is normally about 17 degrees. However, some autokeratometers work with different collimator angles to measure the asphericity along meridians. The keratometer actually presents an average measurement using two small areas that are separated from each other (depending on the device and the radius of curvature of the cornea, from 2.0 to 3.5 mm). So, the apex is not measured but estimated to be spherical between the measured areas. In irregular corneal surfaces and/or a decentered corneal apex (as in keratoconus), this may cause clinically relevant inaccuracies. Also, the range of corneal curvatures that ensure proper images for measurements is limited (usually from 6 to 9 mm). Furthermore, the periphery of the cornea is not measured using standard keratometric methods. A problem in keratometry is also that the measurement is observer dependent. Errors by the observer are misalignment, improper positioning of the mires, ambiguity by distorted mires, focusing, and, most important, accommodation by the observer. In most keratometers errors in focusing are restricted by using a Scheiner disk (double image if out of focus) or collimated mires and telecentric viewing systems (accommodationindependent systems).
Although strictly qualitative, the keratometer can still give the experienced user some information by judging the distortion of the imaged mires on corneal irregularities, tear film quality, and, indirectly, the fit and front surface quality of soft contact lenses. To decrease inaccuracies
and also to reduce the inherent problem that the object is not placed in infinity and thus the image is not formed exactly at the focal plane of the cornea, Mandell11 developed keratometers with a long working distance and small objects (small mire keratometry). With these devices he performed measurements of the peripheral corneal curvature by having the patient fixate on a movable off-axis light source. The need for extra information on the corneal periphery can be easily deducted from Figure 3.1, if one realizes that the smallest contact lens has a diameter of 8.0 mm and classic keratometry only provides information on an area of around 3.0 mm (around 8% of the corneal surface).
and also to reduce the inherent problem that the object is not placed in infinity and thus the image is not formed exactly at the focal plane of the cornea, Mandell11 developed keratometers with a long working distance and small objects (small mire keratometry). With these devices he performed measurements of the peripheral corneal curvature by having the patient fixate on a movable off-axis light source. The need for extra information on the corneal periphery can be easily deducted from Figure 3.1, if one realizes that the smallest contact lens has a diameter of 8.0 mm and classic keratometry only provides information on an area of around 3.0 mm (around 8% of the corneal surface).
Using the principle of off-axis fixation devices, Wilms12 developed a method that can be used with most ordinary keratometers and delivers an estimation of e-values at 30 or 25 degrees from the central axis (Fig. 3.7). Apart from the fact that it is often difficult to obtain reliable peripheral curve data from the periphery of the cornea, it also should be considered that two different methods are being postulated—tangential and sagittal curves—which are difficult to compare.13
In summary, the (auto-) keratometer is a relatively easy-to-use device that, in normal corneas, provides average information on corneal curvature, including amount and axis of astigmatism. In contact lens practice it is successfully used as an initial step to find parameters for a trial lens prior to evaluation by an experienced practitioner. More experienced users can also gain information on the quality of the central part of the corneal surface, the tear film, and the front surface of a soft contact lens.
Keratoscopy and Corneal Topography
Strictly, the name keratoscopy means viewing the cornea; therefore, the original Placido disk is a true keratoscope in the hands of the practitioner looking at the formed image. With photographing the image, the name of the device has historically been changed to photokeratoscopy. Examples of photokeratoscopic images are given in Figures 3.5 and 3.6.
When viewing these images, the qualitative information that can be gained is very evident for a trained clinician. Compared to the keratometer, the photokeratoscopic images give information on a relatively small area, but definitely a larger area than just two points.
With the replacement of the photo camera by a CCD camera, the name of the device was changed to a videokeratoscope. Over time, the name was changed to videokeratograph or, more
common and most widely used, corneal topographer after the implementation of computerassisted software algorithms to analyze the picture.
common and most widely used, corneal topographer after the implementation of computerassisted software algorithms to analyze the picture.
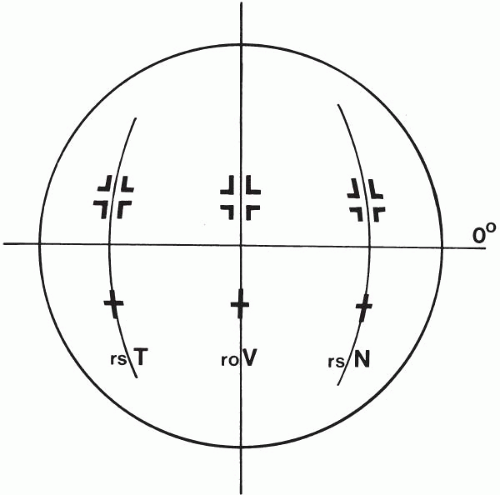 ▪ FIGURE 3.7 The areas measured using sagittal topography as proposed by Wilms. Note that the horizontal meridian is measured in the periphery with the keratometer mires in a vertical position. |
The name corneal topography implies that the topography of the cornea is exactly measured. Is this true? Is the picture that is displayed as a color-coded map the true shape (topography) of the entire cornea? The answer could be no or sometimes yes, but important for clinical applications, the correct answer is “we don’t know.” The reason for this lies in the inherent problem of using a reflected image of an unknown surface that, in itself, is the object of the measurement. Without discussing complicated optical mathematics, some understanding of these inherent problems is useful for practitioners to understand differences between the design of corneal topographers and the interpretation of corneal topographic maps as discussed later in this chapter. Recommended reading in this respect is the classic article by Mandell, “The Enigma of the Corneal Contour.”14
Reflection Topography
Reflection follows the simple rules of Snell’s law, where the incidence ray of light and the reflected ray of light form equal angles with the normal to the surface. In corneal topography, a picture is analyzed, from which it is known that the incident rays are coming from the Placido disk and the reflected rays are coming from the cornea. The advantage over keratometry is that with a flat Placido disk, a two-dimensional object is created so that more points can be evaluated. The problem is, however, that it is unknown where the image exactly was and where in space the reflection occurred. So finding the normal for multiple rays, which is essential for reconstruction of the corneal surface, becomes difficult. Furthermore, it is desired to measure as large an area of the cornea as possible. For this, the use of a large disk would be indicated. However, with large disks the peripheral rays will incident on a very skewed angle compared to the rays more centrally, and also most of these rays will be obscured by the eyelids. Even more complicated is that the image of a large disk is not flat but curved, so the image space becomes three-dimensional. For all of these reasons, modern corneal topographers use a curved or cone-shaped pattern of rings and try to diminish the working distance as much as possible. If the cornea happened to have a spherical shape, its shape would be easy to measure and actually keratometry would be satisfactory. The ironic fact is that the normal cornea is not spherical and that our specific aim is to actually measure the deviations from the sphere. To do so, the data must be fit to mathematically assumed shapes. The assumed shapes could be a sphere, an ellipse using e-values, various polynomials, or splines.
To measure the shape of the cornea with high resolution, one would think that as many as possible rings in the target would be beneficial. This is true, but as can been observed from Figure 3.6A,B compared to Figure 3.5, both the contrast and the order of the rings (lost rings or ring jam) in the image become problematic for software analysis. Some topographers analyze Placido ring borders by using different colors for the outer and the inner boundary of the ring. This way, confusion of rings may be reduced.
Another serious problem, as can be recognized from Figure 3.6A,B, is alignment of the ring target with the center of the cornea. Slight decentration would give an entirely different picture of the rings in the image. A normal cornea could, with decentered imaging, present as a keratoconus pattern. Also, shape algorithms do need a central reference point (with the exception of splines to some extent). In Placido ring imaging the real center is not imaged. This is not a problem for normal corneas, where it can be estimated, but in a keratoconic eye, where the top of the cone is usually not at the geometric center of the cornea, it can be problematic. Also, there is no such concept as a spherical apex area in keratoconus. Odd topographic maps may be seen as a result of this. More on this topic will be discussed later in this chapter under Indexes for Irregularity.
A problem in interpretation of topographic maps is that via viewing a map one could determine that the radius of curvature somewhere on the cornea is, for example, 7.5 mm (or if a
dioptric map is used, 45.00 D). But what does this mean? Is the cornea steep, or is it a local steepness, or maybe a flatter area on a very steep cornea? Even more, what is the position of this steeper or flatter area on the slope of the cornea? It is like walking in an area with hills. You see the curve and you might feel the slope while walking, but are you on a mountain at 6,000 feet high, or on the hill next to your house at the beach? To have access to that knowledge, a height map is needed to really know where you are. The same is true with local corneal curvature data. Here the problem is that a Placido disk inherently estimates radii of curvature where ideally a height map would be desired. Therefore, most modern corneal topographers also present height maps. Although these maps are still derivatives from curvature, by using fast and smart algorithms combined with logical iterative/interpolation/extrapolation processes they can (given a reasonable starting point in the Placido disk image) be reasonably accurate. These data are ideal when designing and manufacturing custom contact lenses.
dioptric map is used, 45.00 D). But what does this mean? Is the cornea steep, or is it a local steepness, or maybe a flatter area on a very steep cornea? Even more, what is the position of this steeper or flatter area on the slope of the cornea? It is like walking in an area with hills. You see the curve and you might feel the slope while walking, but are you on a mountain at 6,000 feet high, or on the hill next to your house at the beach? To have access to that knowledge, a height map is needed to really know where you are. The same is true with local corneal curvature data. Here the problem is that a Placido disk inherently estimates radii of curvature where ideally a height map would be desired. Therefore, most modern corneal topographers also present height maps. Although these maps are still derivatives from curvature, by using fast and smart algorithms combined with logical iterative/interpolation/extrapolation processes they can (given a reasonable starting point in the Placido disk image) be reasonably accurate. These data are ideal when designing and manufacturing custom contact lenses.
Reading of a height map is quite different from a curvature map. A height map representing the total, absolute sagittal height of the cornea actually would not give any detail at all. All it would show is that the central cornea is higher than the periphery, which is not really a surprise. It becomes useful only after matching the corneal surface with a so-called “best-fit sphere” (or sometimes “a best-fit oval”). Everything that is higher (meaning being closer to the observer) is color coded with warmer colors; everything that is positioned farther away from that shape is presented with cooler colors. Therefore, what the exact (and actual) shape of the cornea is can be immediately observed.
In summary, reflection corneal topographers, compared to keratometry, are ideal in obtaining more information on an extended area of the cornea, but still do not measure the complete corneal surface. They are not difficult to use, but care should be taken in obtaining both proper alignment and focusing. Looking at the image before processing is recommended, and proper interpretation of the different maps is a key consideration. This topic will be further discussed later in this chapter under How to Use a Corneal Topographer.
Projection Topography
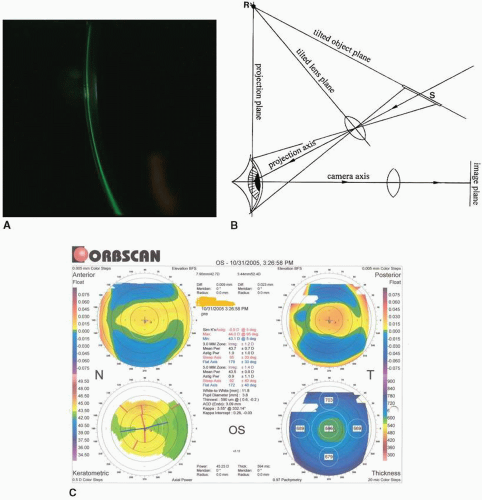
Appreciating the disadvantages of reflection systems, alternatives to the Placido disk-based corneal topographers have been developed.15,16,17 Most of these devices are more complicated in use, expensive, or more used in research settings than in routine clinical settings. To explain the principles of using a projecting light source, three different possibilities are described here. The first is projecting a set of lines on the cornea (Maastricht Shape Topographer, or MST); the second is the use of a scanning slit such as that used in Orbscan and Pentacam systems. The MST, based on Fourier profilometry, is able to present a height map of the total area composed to the instrument (Fig. 3.8A). The system projects from two directions a line pattern on the front surface of the eye in which fluorescein acts as diffusing medium. Because the line patterns are viewed by a central camera, they become, depending on the shape of the eye, curved in the image (Fig. 3.8B). Fourier analysis can transform this information to height data, and from there it is possible to create cross sections of the cornea and sclera including limbal topography (Fig. 3.8C). As with Placido disk devices, a good image is essential. Advantages of the MST include that it measures shape directly and—especially important in contact lens designing—presents height information on the entire eye front surface.
The principle of a scanning slit as in the Orbscan and Pentacam devices15 can be easily appreciated from a cross section view of the cornea (Fig. 3.9A), routine for eye care practitioners. In the slit image the profile of the cornea front and back surface can be observed. Unfortunately, this is only one meridian and if the incidence angle of the slit were changed, a dramatic change would be observed. In the Orbscan device a scanning slit is used to obtain multiple images over many meridians. To overcome distortion by different incidence angles, a Scheimpflug correction system is built in (Fig. 3.9B). From the many imaged slits the corneal shape, both front and back surface, can be computed. So, actually indirect pachymetry
is performed. The results are presented in color-coded maps, including corneal thickness data (Fig. 3.9C). Advantages of the Orbscan device are that it is able to present height data on both the front and back surface of the cornea.
is performed. The results are presented in color-coded maps, including corneal thickness data (Fig. 3.9C). Advantages of the Orbscan device are that it is able to present height data on both the front and back surface of the cornea.
Optical Coherent Tomography
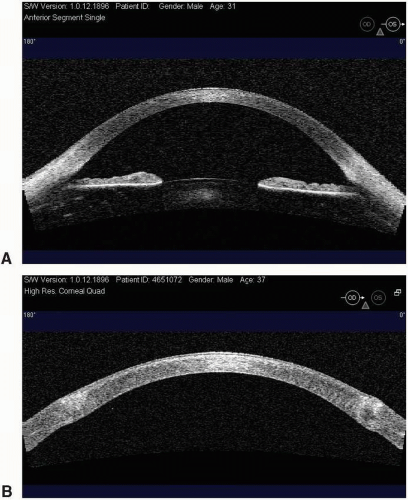
Recently, devices have been developed that are able to image the front segment of the eye based on optical coherent tomography (OCT). The principle behind these devices is a Michelson interferometer, in which time differences using two imaging paths from the same target are used to compute distance data. One imaging path is calibrated for the device, and
the other path contains the object to measure (in this case the eye). Next to the front segment of the eye (Fig. 3.10A), the cornea can also be measured using so-called high-resolution imaging (Fig. 3.10B). From these images the real corneal height topography can be obtained. At present not much information on the accuracy and reproducibility of OCT for work in the contact lens field is available. It appears to be a promising device in the future, although it is still relatively expensive at the present time.
the other path contains the object to measure (in this case the eye). Next to the front segment of the eye (Fig. 3.10A), the cornea can also be measured using so-called high-resolution imaging (Fig. 3.10B). From these images the real corneal height topography can be obtained. At present not much information on the accuracy and reproducibility of OCT for work in the contact lens field is available. It appears to be a promising device in the future, although it is still relatively expensive at the present time.
Clinical Potential of Devices
The question about which one of all the technologies mentioned is the best cannot be easily answered. It largely depends on the aim of the application. Corbett et al.18 mentioned four considerations regarding this question: the kind of required measurement, the kind of eye surface, the kind of situation, and the kind of required presentation. If the corneal surface is considered to be an optical surface, a parametric measurement might be indicated with the advantage that considerable sensitivity is gained. Most devices based on specular reflection, including the Placido disk-based corneal topographers, measure parametrically. If the local corneal anatomy is important in the diagnosis, devices based on scattering can offer interesting modalities (e.g., pachymetry). Should it not be the optical performance but the shape that is the object of the diagnosis (e.g., pre- and postoperative evaluation or contact lens fitting), devices based on diffuse reflection offering direct height measurements can be more useful. Sometimes a diffusing membrane or simply a thin soft contact lens may be beneficial. Dry corneas, for example, exclude effective use of specular reflection, whereas during surgery no fluorescein can be used as this penetrates the stromal tissue.
For corneas with a regular surface, a mirrored image, which is easily acquired with a Placido disk-based corneal topographer, is adequate. For irregular corneas, of which the shape is to be determined, detailed height mapping might be more accurate when obtained with a nonparametric measurement using projection principles.
▪ HOW TO USE A CORNEAL TOPOGRAPHER
A corneal topographer is a very powerful tool, and the primary limitation appears to be the amount of data that is provided, which might be too overwhelming to be of practical use. This part of the chapter on corneal topography will discuss the necessary insights in how to use the tools available in the giant toolbox that a topographer is, and how to optimize usage of the instrument.
Measuring Procedure
Most of the topographers, especially so in contact lens practices, are the reflection systems, and these will be further discussed in detail here. One of the primary disadvantages of a reflection system topographer is the limited area that typically can be measured. To measure the maximal surface area of the cornea, it is important to first minimize the upper eyelid interference, which can cause shadows on the cornea, leading to missing data points. This is typically accomplished by asking the subject to make “large eyes.” If this is not sufficient, the eyelid can be held up by a cotton swab. However, it is important for there to be an absence of pressure on the eyeball, as pressure can easily cause corneal curvature changes. It is preferable to use the orbital rim as a resting point. The subject’s nose also can cause shadows on the cornea, which may lead to missing data points. To avoid this, the patient can be asked to move his or her head slightly: if the right eye is being measured, ask the patient to rotate his or her head slightly to the left, while emphasizing the importance of fixation straight ahead. This way the nose will have a lesser impact on the topography picture that is taken.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree