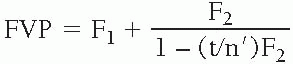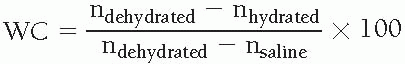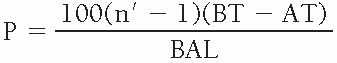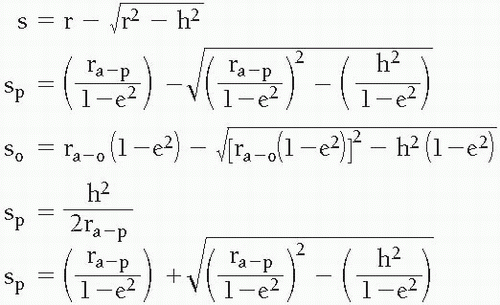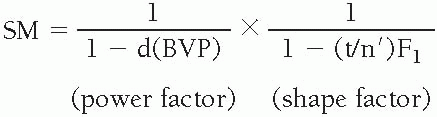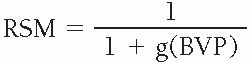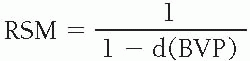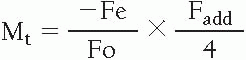▪ FORMULAE FOR CONTACT LENS OPTICS
Reflection for rays at near-normal incidence:
R = [n’ – n)/(n’ + n)]2
Back vertex power:
Front vertex power:
where
R = reflectance from 0 to 1.0
n = refractive index of medium surrounding surface
n’ = refractive index of medium within lens
t = center thickness of contact lens (m)
BVP = back vertex power (D)
FVP = front vertex power (D)
F1 = front surface power (D)
F2 = back surface power (D)
Law of Gladstone and Dale:
nhydrated = npVp + nsVs
Water content:
where
r = radius of curvature of contact lens surface (m)
F = refractive power of surface
Vp’ Vs = fraction of material volume devoted to polymer, saline
np’ ns = refractive indices for the polymer, saline in a hydrogel
WC = water content, in %
Astigmatic addition:
CPA = CA + IA
Diagnostic lens formula:
FCLP = DCLP + OR − ΔLLP
CPR = CLR + OR + LLP and FCLP = CPR − LLP
Lacrimal lens power:
LLP = BC − K
where
CPA = astigmatism at corneal plane (DC)
CA = corneal astigmatism (DC)
IA = internal astigmatism (DC)
BC = base curve (D)
K = keratometry reading (D)
LLP = lacrimal lens power (D)
ΔLLP = change in LLP (D)
CPR = corneal plane refraction (D)
CLP = contact lens power (D)
FCLP = final CLP (D)
DCLP = diagnostic CLP (D)
OR = overrefraction (D)
Empirical effect of flexure on soft contact lens power:
ΔF = −300(t)[(1/rk2) − (1/r22)]
Prism thickness formula:
Meniscus lens thickness formula:
CT + s2 = ET + S1
where
t, CT = center thickness of lens
rk = radius of curvature of cornea
r2 = base curve radius of lens
ΔF = change of refractive power (D)
ET = uncut edge thickness of lens
s1, s2 = front, back surface sagittal depths
Sagittal depth equations:
where
e = eccentricity
ra = apical radius of curvature
P = prismatic power in prism diopters (Δ)
h = half of the chord diameter, 2h
ra-p = prolate apical radius of curvature
ra-o = oblate apical radius of curvature
sp, so = prolate, oblate sagittal depths
BVP = back vertex power (D)
BT = thickness of prism base
AT = thickness of prism apex
BAL = length of the base-apex line
Relative Spectacle Magnification
Spectacle magnification:
Axial anisometropia:
Refractive anisometropia:
*
Comparison of contact lens to spectacle lens power factors:**
where
BVP = back vertex power (D)
d = stop distance, from back vertex of correcting lens to entrance pupil of eye (m)
***t = center thickness of correcting lens (m)
SM = spectacle magnification relative to 1.0
RSM = relative SM relative to 1.0
g = distance from anterior focal point of eye to back vertex of correcting lens (m)
Magnification of spectacle-contact lens telescope:
****
where
Mt = magnification of telescope relative to 1.0
Fo = power of objective, spectacle lens (D)
Fe = power of eyepiece, contact lens (D)
Fadd = power of add in spectacle lens (D)
*In keratometric diopters, n’ = 1.3375 and n = 1.0000.
*When an OR of zero is intended for the final lens order, these two equations are equivalent.
**Note that here, h is in cm.
*Note similarity to power factor of spectacle magnification.
**BVP here is that of the spectacle lens.
***Stop distance = vertex distance + 3 mm.
****When no add is in the spectacle lens, the second factor (Fadd/4) is omitted from this equation.
▪ KEY WORDS OF CONTACT LENS OPTICS
Corneal reflex
Fresnel’s formula of reflection
Gullstrand exact schematic eye
Purkinje-Sanson images I-IV
Specular reflection
Tear fluid meniscus
Black line
Sclerotic scatter
Endothelial mosaic
Guttata
Refractive index
Law of Gladstone and Dale
Maurice’s lattice theory
Epithelial edema
Stromal edema
Central corneal clouding (CCC)
Sattler’s veil
Fick’s phenomenon
Birefringence
Optical anisotropy
Isochromes
Isoclinics or isogyres
“Against” motion
“With” motion
“Scissors” motion
Epithelial microcysts
Epithelial vacuoles
Epithelial bullae
Epithelial “microdeposits”
Keratometry limitations
Refractive index of keratometer
Corneal topography
Corneal apex
Visual axis
Central corneal cap
Elliptical surface
Regular and irregular toricity
“Semi-meridians”
Entrance pupil
Flare and glare
UVR: UV-A, UV-B, UV-C
Cobalt filter
Ultraviolet lamp
“Phantom fluorescein effect”
“Myopic creep”
Back vertex power
Front vertex power
“Sagittal depth effect”
Water content, equation
Blotting technique
Wet cell
Correction factor
Vertex distance
Effective power
“Lacrimal lens”
Lacrimal lens theory
K readings
“Steeper than K”
“Flatter than K”
“On K”
Masking of corneal shape
Overrefraction
Overkeratometry
With-the-rule
Against-the-rule
Residual astigmatism
Spherical rigid contact lens
Front toric rigid contact lens
Back toric rigid contact lens
Bitoric rigid contact lens
Spherical power effect
Cylindrical power effect
Rule of thumb for BCR changes
Flexure of soft lenses
“Equal change hypothesis”
Wrap factor
“Constant volume and thickness”
Flexure of rigid lenses
Warpage, regular and irregular
Back-surface bifocals
Crossed-cylinder effect
Sagittal depths
Sphere
Ellipse, prolate and oblate
Parabola
Hyperbola
Eccentricity
Shape factor (1 – e2)
Accommodative demand
At spectacle plane
At corneal plane
At lenticular plane
Prism diopter
Prentice’s rule
Vergence demand
Pre-presbyopic myopes
Spectacle magnification
Power factor
Shape factor
Stop distance
Relative spectacle magnification
Axial ametropia
Refractive ametropia
Knapp’s law
Field of view
Field of fixation
“Ring scotoma”
“Ring diplopia”
Off-axis aberrations
On-axis aberrations
Spherical aberration
Coma
Radial astigmatism
Curvature of field
Distortion
Chromatic aberration
Prismatic dispersion
Spectacle-contact lens telescope
Alternating vision
Simultaneous vision
Monovision
Modified monovision
Diffractive bifocal contact lens
“Holographic” bifocal contact lens
Fresnel lens principle
Fresnel half-wavelength zones
“Full aperture” bifocal lenses
“Reduced aperture” lenses
Pupil dependence and independence
Pupil size dependence
Pupil location dependence
Coroneo effect
Rizzuti’s sign
Liquid crystal
Polarization