, Maneli Mozaffarieh1 and Hans Bebie2
(1)
Department of Ophthalmology, University of Basel, Basel, Switzerland
(2)
Institute for Theoretical Physics, University of Bern, Bern, Switzerland
Abstract
This book was written for ophthalmologists and light will be one of our main topics. We assume that all of us – the authors and the readers alike – marvel about all the various ways that light appears. When we see the pole star in the night sky − because the process of doing it is apparently so self-evident − we are hardly aware that, through this viewing, we are participating in a fantastic process. The light left the star’s hot atmosphere in Newton’s time and was then underway, solitarily, through almost empty space until it entered our atmosphere and then passed almost unimpeded through several billion molecular shells. Finally, focused on the retina by the cornea and lens, it triggered a state change in rhodopsin molecules that, via a chain of chemical amplifications, led to the hyperpolarization of photoreceptors and fed electrical signals into the brain’s neural network. At the end of the process stands the mystery of how the signal then arrives in conscious awareness.
This book was written for ophthalmologists and light will be one of our main topics. We assume that all of us – the authors and the readers alike – marvel about all the various ways that light appears. When we see the pole star in the night sky − because the process of doing it is apparently so self-evident − we are hardly aware that, through this viewing, we are participating in a fantastic process. The light left the star’s hot atmosphere in Newton’s time and was then underway, solitarily, through almost empty space until it entered our atmosphere and then passed almost unimpeded through several billion molecular shells. Finally, focused on the retina by the cornea and lens, it triggered a state change in rhodopsin molecules that, via a chain of chemical amplifications, led to the hyperpolarization of photoreceptors and fed electrical signals into the brain’s neural network. At the end of the process stands the mystery of how the signal then arrives in conscious awareness.
The question “What is light?” has always occupied us. In 1760, in one of his 200 tutorial letters, Euler1 wrote, “Having spoken of the rays of the sun, which are the focus of all the heat and light that we enjoy, you will undoubtedly ask, What are these rays? This is, beyond question, one of the most important inquiries in physics.” Today, physicists assume that the physical nature of light and the laws of its interactions with matter are completely known.2 The theory is characterized by the simultaneous concepts of light as electromagnetic waves, on the one hand and, on the other hand, as a stream of particles (photons). It seems that any given phenomenon can be easily understood in terms of one of these two models. The wave model easily explains the fundamental limits of visual acuity due to the diffraction of light passing through a pupil, while the photon model forms a suitable vehicle for understanding the absorption processes in a molecule. We shall deal with both of these models and explain how it is that the fact that both are simultaneously true does not represent a contradiction.
In the following sections, we shall be concerned with the question “What is light?” We start with simple assertions from the photon and wave models and then go on to address the highly interesting relationship between them.
1.1 What Did Einstein Have to Say About Blue and Red Light?
When we open a textbook on light and optics, we soon find a picture showing the refraction of light as it passes through a glass prism and how the red, orange, yellow, green, blue, and violet colors appear in that order. A rainbow has these colors in exactly the same order. With the numbers shown on the right in Fig. 1.1, we note what Einstein postulated in 1905 about the nature of light: it consists of corpuscles (photons), and the energy of red light photons amounts to ca. 2 eV, while that of blue light is ca. 3 eV (electron volts3). In other words, light has corpuscular properties, light carries energy, and all photons in the light of a given color have the same energy. This forms the contents of the so-called quantum hypothesis of light. Obviously, a prism can separate the photons of a white beam of light according to their energies. Our eyes also react to these small energy differences: depending on the photon energies, they appear to our minds in their associated colors.
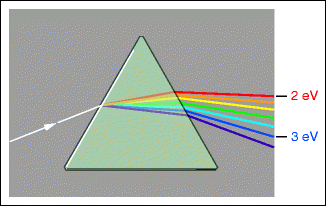

Fig. 1.1
Decomposition of white light by a glass prism. If we separate out a small range in the spectrum, we obtain monochromatic light. Photons of red light have energies of 2 eV; those of blue light have 3 eV
The fact that light is associated with energy is the rather self-evident background to what Einstein said; after all, we let ourselves be warmed by sunlight. However, from the 1,000 W of light power per square meter that enters the atmosphere, only half of it is visible light; the rest consists of infrared and ultraviolet radiation.
Above, we mentioned an initial aspect of light properties without trying to make it plausible. It is well known that Newton already believed that light consisted of particles, but Einstein made this concept more precise. By the way, how big is energy of a few eV? Obviously, it is sufficient to excite rhodopsin and trigger an electrochemical process. A few such processes, taking place in the rods of a fully dark-adapted eye, are enough to create a conscious perception of light. Another possibility of conceiving this is the fact that a few eV of energy suffice to raise a water droplet roughly 1 μm in size by 1 μm.
An impressive demonstration experiment that accentuates light’s particle character is elucidated in Fig. 1.2. It is based on the ability of special detectors (e.g., photomultipliers) to react to each photon received with a usable electrical pulse. This can be amplified and fed to a loudspeaker. When a ray of light is so strongly attenuated that the detector absorbs only a few dozen photons per second, a crackling is heard consisting of one click per photon. If the light ray is interrupted, the crackling stops immediately. More precisely, its frequency returns to the so-called dark frequency, triggered by spontaneous thermal effects in the detector.


Fig. 1.2
Single photons can be detected individually and made audible as “clicks” in a loudspeaker. Light source (1), strongly attenuating filter (2), photodetector (photomultiplier, (3), electronic amplifier (4), loudspeaker (5). On the right, a typical random series of “clicks” as a function of time is illustrated
Light consists of photons – we use this language especially when describing elementary processes that take place in the interactions between light and matter. A single photon excites a single retinal molecule; or an excited atom emits a photon. The absolute threshold of the eye can be expressed in a memorable way in the “photon language.” In a completely dark-adapted human eye, a stream of approximately 1,000 photons per second entering the pupil (e.g., at night, from a barely visible star) is sufficient to trigger a consciously perceptible stimulus. The same is true for a brief flash of approximately 100 photons entering the pupil even though only a few photons are absorbed by rhodopsin.
We have not yet discussed the basis behind the quantum hypothesis of light. We are only indicating the questions and problems that Einstein solved at one go:
1.
With the quantum hypothesis, Planck’s law of the thermal emission of light by hot matter can be theoretically established (this law will be covered in Chap. 3).
2.
Without the quantum hypothesis, light would have an infinitely large entropy (inner disorder) – a theoretical argument that was quite prominent for Einstein’s deliberations.
3.
The quantum hypothesis explains the photoelectric effect; namely, that the energies of electrons, which are ejected from a metal surface when light strikes it, are independent of the light’s intensity and depend only on its color (Fig. 1.3).
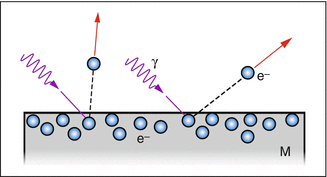


Fig. 1.3
The photoelectric effect. Photons are able to knock electrons out of a metal surface. In doing so, the photon transfers all of its energy to the electron and must transfer at least the energy necessary for it to leave the metal’s surface. The size of this so-called work function depends on the metal. For zinc, for example, it amounts to 4.3 eV. The energy that remains after the work function has been overcome is taken by the electron as its kinetic energy. For a material with a work function of 2.5 eV, the effect occurs with blue light but not with red light. An essential feature of the photoelectric effect is that the energies of the electrons do not depend on the light intensity but, rather, only on its color. M metal, γ photon, e– electron

Fig. 1.4
Thomas Young
1.2 Light as a Wave
For a moment, we shall forget about photons and turn to a second, totally different answer to the question concerning the nature of light: light as a wave phenomenon. As evidence, Young4 developed a very convincing experiment, the double slit experiment, which will be discussed later (Fig. 1.4). For the purposes of orientation, we also assume some facts without substantiating them: red light has a wavelength of ca. 0.7 μm, while that of blue light is ca. 0.45 μm. Figure 1.5 shows more generally the wavelengths of the various colors.
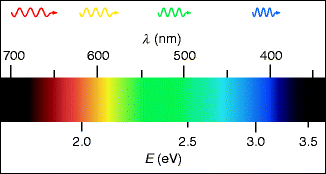

Fig. 1.5
The light spectrum. Each position in the spectrum has an associated wavelength. The wavelengths are indicated above and the photon energies below the colored spectrum
However, when we look around, we see the sun, clouds, blue sky, colored surfaces, light sources, our mirror images – but no waves. Indeed, the wave properties of light are somewhat hidden from the eye due to the very small wavelengths involved (0.4–0.8 μm). The wave properties of light are proven most convincingly, though, with a phenomenon that is observable only with waves: light can cancel out light, just as a peak and a valley of two overlapping water waves neutralize one another. This phenomenon is called interference (Fig. 1.6) and forms the basis for the double slit experiment that we shall now discuss.
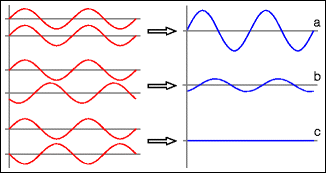

Fig. 1.6
Constructive and destructive interference. (Left) Pairs of overlapping waves. (Right) The sum of the two components. (a) Constructive interference with the same phase with the maximum sum. (b) 150° phase shift; the resulting amplitude is weaker. (c) Cancellation with a phase difference of 180° (half wavelength) in that the peaks coincide with the valleys
1.2.1 The Double Slit Experiment
Young’s double slit experiment is deemed decisive evidence of the wave nature of light. Let us start with a single slit. Due to diffraction, as light passes through a single tiny opening, it fans out and produces a uniform illumination of the screen (Fig. 1.7). If a second nearby hole or slit is opened, a pattern of stripes appears on the screen (Fig. 1.8). At certain places, the light coming from the two openings is extinguished. These are precisely the locations where the path differences from the two openings amounts to half a wavelength: a wave crest meets a wave depression.5
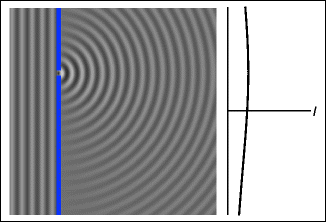
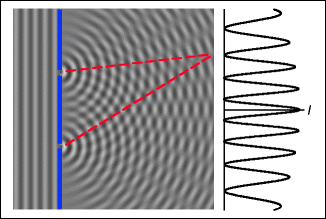

Fig. 1.7
A wave, coming from the left, passes through a single, small opening and spreads out to the right due to diffraction. Averaged over a few vibrational periods, the screen (at the right) becomes uniformly illuminated. I intensity on the screen

Fig. 1.8
The double slit experiment. Light coming from the left. The screen at the right is illuminated by the light coming from the two openings. An interference pattern appears on the screen. Cancellation (destructive interference) occurs at those locations where the paths from the two openings differ by an odd number (1, 3, 5, …) of half wavelengths. The lengths of the red paths differ by 5/2 wavelengths. I Intensity on the screen
From the geometric arrangement and the interference pattern, Young could even derive the wavelength. He found the values given above. But what is it that actually vibrates? That was the big question of his time.
1.2.2 A Freehand Interference Experiment
The principle of the interference experiment with light can be observed with the simplest means – with the naked eye (Fig. 1.9). The invested time will be repaid by acquiring a more direct relationship with the wave nature of light. Poke two tiny holes into a piece of paper, as close together as possible and, at night, observe a small, bright source of light (e.g., a street lamp at a large distance) through these openings. Through the interference of the light coming from the two openings, a striped pattern arises on the retina that appears to be about the size of the moon. The dark areas arise there where the difference in pathway from the two openings amounts to an odd number of half wavelengths – light waves with a phase difference of 180° extinguish each other. In terms of electrodynamics, at this point, electrical fields with opposite directions meet. The clearest patterns can be seen with monochromatic light. As light sources, the yellow-orange street lamps (sodium vapor lamps, λ = 588 nm), for instance, are very well suited. The mechanism is exactly the same as in Young’s double slit experiment. For a distance between the holes of 6 mm, the bright stripes on the retina have a separation of roughly 10 μm, corresponding to a visual angle of about 2 min of arc. A model for this demonstration is an apparatus, invented in 1935 by Yves Le Grand, for the interferometric determination of visual acuity (see Sect. 4.2).
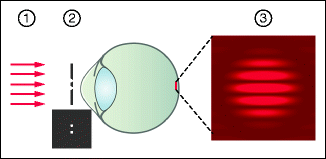

Fig. 1.9
An easy version of Young’s double slit experiment: observing light interference with the simplest means. (1) Light from a distant street lamp. (2) Apertures, consisting of two needle holes (ca. 0.2 mm diameter) close together (ca. 0.6 mm) in a piece of paper. (3) Interference pattern on the retina (ca. 0.2 mm diameter, corresponding to 0.5°)
1.2.3 Diffraction
A further manifestation of the wave nature of light is diffraction: When encountering an edge or passing through an aperture, the light’s pathway is bent, i.e., deviated from its normal straight line of travel. For example, the play of colors seen when looking at a distant street lamp through an opened umbrella is due to diffraction as the light passes through the periodic arrangement of the fibers of the umbrella textile. Diffraction also occurs when light passes through the pupils of our eyes. This results in a fundamental limitation of visual acuity with small pupils (Sect. 19.1). Due to diffraction, the resolution of a light microscope is also restricted to structures the size of a half wavelength (Sect. 19.4).
Diffraction occurs with every wave phenomenon. With surface waves on water, they can be observed directly: for example, when water waves pass through an opening (Fig. 1.10). For openings that are much larger than the wavelength, the wave continues without the diffraction being noticeable. However, the narrower the opening is in comparison to the wavelength, the more pronounced the deviation of the wave’s direction will be. In the limiting case of an arbitrarily small opening, the wave on the other side spreads out with the same intensity in all directions.


Fig. 1.10
Diffraction of water waves when passing through a harbor entrance. The larger the entrance is in comparison with the wavelength, the less apparent the diffraction will be
As a variation of the experiment in Sect. 1.2.2, we can try seeing the diffraction image made by a round aperture. This is done by viewing a distant light source (approximating a point source) through a tiny hole (Fig. 1.11).
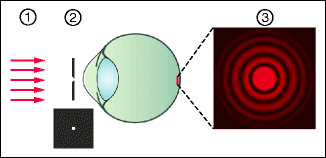

Fig. 1.11
Diffraction rings (3) on the retina created by light (1) coming from a point-shaped source and through a tiny hole (2). As an aperture, a tiny hole is made by sticking a needle point through a piece of paper and this is then held very near the eye
1.3 Light as an Electromagnetic Phenomenon
Interference and the diffraction of light can be explained by assuming that light is a wave phenomenon without being specific about the precise nature of the vibrations that propagate through empty space in the form of light. We will start with a clear proposition: light is an electromagnetic wave. The waves that travel back and forth between mobile telephone transmitters and cell phones are also electromagnetic waves – the difference lies only in the wavelengths: the physical laws behind them are exactly the same (Fig. 1.12).
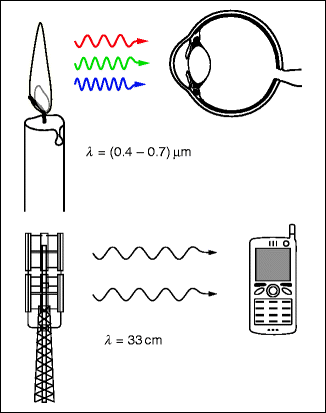



Fig. 1.12
Light as an electromagnetic wave. The difference between light and cell phone waves lies in their respective wavelengths λ (cell phone: λ = 33 cm, light: λ = 0.4–0.7 μm)

Fig. 1.13
Michael Faraday

Fig. 1.14
James C. Maxwell
As indicated by the section title, a light ray can be understood as a combination of very rapidly oscillating electric and magnetic fields that propagate in empty space at the speed of light. How can we imagine these fields? Briefly put, magnetic fields affect magnetized needles and electric fields exert force on electrically charged particles, e.g., on free electrons or ions. There is an electric field, for example, between the two poles of an electric plug. If the two poles come close enough, the electric field between them is so strong that sparks will be produced in the gap.
A bar magnet produces a magnetic field. It can be perceived by a magnetized needle (such as in a compass) that aligns itself with the direction of the magnetic field. We now consider the situation in which a bar magnet rotates. It generates a magnetic field such that its direction and strength will change at every fixed location. It will oscillate in step with the rotation. Now the laws of electrodynamics take effect: a changing magnetic field engenders an electric field. The rotating magnet also creates an electric field that again oscillates in step with the rotation. Now, another of the basic laws of electrodynamics enters: for its part, a changing electric field once again creates a magnetic field. This mutual creation of changing fields propagates in space with the speed of light. We will not consider the process of the propagation in more detail, but sound and water waves also propagate away from a local disturbance.
With the rotation of the bar magnet, we create an electromagnetic wave that spreads out in all directions at the speed of light. At every fixed location in space, it vibrates in step with the rotation. If the bar magnet were to be rotated with a frequency of 108 Hz, radio waves would be produced – and when it is rotated even more rapidly, with a rotation frequency of 5∙1014 Hz, yellow light would be seen. Only atoms, though, can achieve such frequencies.
Initially, Maxwell’s6 1864 hypothesis that light consists of electromagnetic waves was purely speculative: at the time, electromagnetic waves were not known but only a possible solution to his equations, resulting from his mathematics. We pay tribute to this event here by concerning ourselves with it a bit further. The empirical foundation was created by the great experimenter Faraday7 in the first half of the nineteenth century with his research regarding the emergence of electric and magnetic fields from electric charges and currents, as well as the discovery of the laws of induction (changing magnetic fields create electric fields – the basis for transformers). Maxwell succeeded in comprehending all of these phenomena quantitatively with his four equations.8 In addition, far beyond the laboratory experiments, they exhibited – purely mathematically – a noteworthy solution: electromagnetic waves of any desired wavelength that propagate in a vacuum with a speed of ca. 300,000 km/s – if they were to exist. This speed resulted from the constants measured in the laboratory concerning the relationships between charges, currents, and fields. The agreement with the known velocity of light was spectacular (Figs. 1.13 and 1.14).
< div class='tao-gold-member'>
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


