Fig. 2.1
Graphic representation of vector analysis. (a) An example vector of +2.00 × 60° is depicted in power cross cylinder notation. (b) The same vector is depicted in double-angle cylinder notation, along with its x and y components. (c) Double-angle plot of aggregate astigmatism data, along with the mean vector (red dot) and standard deviation (red line). Each ring represents 0.25 diopters D, and the outer ring represents 1.0 D
2.4 Qualitative Analysis of Surgically Induced Astigmatism
The effect of the incision on the SIA is qualitatively illustrated in four case examples (Fig. 2.2). For all examples, the magnitude of the SIA of the incision to be 0.5 diopters (D) with a coupling ratio (CR) of 1:1; i.e., the amount of corneal steepening orthogonal to the incision is equal to the amount of flattening along the meridian of the incision. In Example A, the incision is made at 180° on a spherical cornea, which creates with-the-rule (WTR) astigmatism postoperatively. In Example B, the incision is made at 90° on a spherical cornea, which creates against-the-rule (ATR) astigmatism postoperatively. In Example C, the incision is made at 180° on a cornea with ATR astigmatism preoperatively. The effect of this on-axis (incision and astigmatism at same meridian) incision is to reduce the magnitude of the ATR astigmatism postoperatively. In Example D, the incision is made at 180° on a cornea with oblique astigmatism preoperatively. The effect of this off-axis (incision and astigmatism at different meridians) incision is to shift the preoperative astigmatism counterclockwise and slightly increase its magnitude.


Fig. 2.2
Qualitative analysis of surgically induced astigmatism (SIA) in four example scenarios. The SIA of the incision is assumed to be 0.5 diopters (D), with a coupling ratio (CR) of 1. In examples (a) and (b), there is no preop astigmatism, and the incision is placed at 180° or 90°, respectively. Examples (c) and (d) illustrate the effect of on-axis and off-axis incisions, respectively
2.5 Surgically Induced Astigmatism
The simplest method for calculating SIA focuses solely on the corneal astigmatism and not the total refractive power of the cornea. To perform this calculation, the pre- and postoperative values for the cylinder magnitude and axis are required. The first step is to convert the pre- and postoperative polar cylinder-axis values to a Cartesian coordinate system with x and y components using Eqs. (2.1) and (2.2) (Fig. 2.1b):



(2.1)

(2.2)
The cylinder magnitude is the corneal curvature along the steep meridian minus the corneal curvature along the flat meridian and will thus be a positive value. The axis is the location of the flat meridian.
Next, the SIA for each x and y component vector is calculated as the difference between the pre- and postoperative values (Eqs. (2.3) and (2.4)):



(2.3)

(2.4)
where x SIA and y SIA are the x and y components of the SIA vector, respectively. Then, the SIA vector is reassembled from Cartesian x and y components back into polar coordinate form using Eqs. (2.5) and (2.6):



(2.5)

(2.6)
Finally, a four-quadrant version of the inverse tangent function must be used to preserve the correct axis orientation using Eqs. (2.7a)–(2.7c) (Fig. 2.3a):

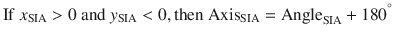


(2.7b)
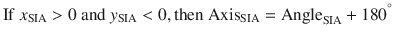
(2.7c)

Fig. 2.3
A four-quadrant version of the inverse tangent function must be used to preserve the correct axis orientation when calculating surgical induced astigmatism (a) and surgically induced refractive change (b)
To compute the aggregate SIA for a given set of eyes, the means of the x and y component vectors are calculated, and the resultant mean SIA vector is reassembled as above. It should be noted that this method assumes that the average corneal curvature does not change; i.e., the “spherical equivalent” is the same before and after surgery.
If the individual patient vectors are displayed on a double-angle plot, the mean vector will represent the centroid of the data. The spread of the SIA data can be represented by an ellipse that is centered upon and extends one standard deviation above and below the mean (Fig. 2.1c). The horizontal and vertical borders of the ellipse are equivalent to the mean x and y vectors ± the standard deviation of the x and y vectors, respectively.
2.6 Surgically Induced Refractive Change
This next method for calculating SIA is a little more versatile and accounts for any change in the average corneal curvature that occurs in combination with the astigmatic change. As proposed by Thibos [9], this method represents spherocylindrical corneal curvature as the sum of a single spherical refractive surface combined with two Jackson cross cylinder (JCC) refractive surfaces. Each of these components can further be represented as a vector, which permits ready calculation of the surgically induced refractive change (SIRC).
To calculate the SIRC, the pre- and postoperative keratometric K readings (K pre and K post) are required. The first step is to convert the pre- and postoperative K readings (K flat @ meridianflat, K steep @ meridiansteep) to positive cylinder form (S, +C × β) using Eqs. (2.8a)–(2.8d):





(2.8a)

(2.8b)

(2.8c)

(2.8d)
where S is the sphere, C is the cylinder, β is the flat meridian, and α is the steep meridian. Next, K pre and K post are converted from positive cylinder form to rectangular Fourier form [M, J 0, J 45] using Eqs. (2.9a)–(2.9c):




(2.9a)

(2.9b)

(2.9c)
The rectangular Fourier form describes an arbitrary spherocylinder that is equivalent to the sum of a spherical lens of power M and two Jackson cross cylinders, one at axis 0° with power J 0 and the other at axis 45° with power J 45.
Next, the SIRC is calculated as the difference between K post and K pre in rectangular Fourier form using Eqs. (2.10a)–(2.10d):



![$$ SIRC=\left[{M}_{\mathrm{SIRC}},{J}_{0\ \mathrm{SIRC}},{J}_{45\ \mathrm{SIRC}}\right] $$](https://i0.wp.com/entokey.com/wp-content/uploads/2018/02/A325183_1_En_2_Chapter_Equ20.gif?w=960)

(2.10a)

(2.10b)

(2.10c)
![$$ SIRC=\left[{M}_{\mathrm{SIRC}},{J}_{0\ \mathrm{SIRC}},{J}_{45\ \mathrm{SIRC}}\right] $$](https://i0.wp.com/entokey.com/wp-content/uploads/2018/02/A325183_1_En_2_Chapter_Equ20.gif?w=960)
(2.10d)
Then, the SIRC is converted from rectangular Fourier form back to conventional positive cylinder form using Eqs. (2.11a)–(2.11d):


(2.11a)




