Purpose
To determine the degree of agreement between 2 mathematical models and 3-dimensional ultrasonography (3DUS) in estimating choroidal melanoma tumor volumes.
Design
Reliability analysis.
Methods
Tumor measurements estimated by 2 mathematical models (designated Formula 1 and Formula 2) were compared to those obtained by 3DUS in 45 consecutive patients with primary choroidal melanoma to determine the percentage agreement between the models and 3DUS.
Results
Both formulas tended to overestimate the tumor volume. Overall, the mean volume differences between 3DUS and Formula 1 and between 3DUS and Formula 2, respectively, were 51.7 mm 3 (95% confidence interval [CI], 187.6 to 84.3) and 23.8 mm 3 (95% CI, 122.5 to 74.8). Excluding mushroom-shaped tumors, the mean volume differences were 52.0 mm 3 (95% CI, 194.9 to 91.0) and 23.0 mm 3 (95% CI, 127.0 to 81.0), respectively. In mushroom-shaped tumors, mean volume differences were 49.9 mm 3 (95% CI, 135.7 to 35.9) and 29.3 mm 3 (95% CI, 87.6 to 29.0), respectively.
Conclusions
The agreement between these mathematical models and the measured 3DUS volume was high. The data obtained in this study show that both formulas provide a simple, fast, and accurate method of estimating tumor volumes in the clinical setting, suggesting that these models could be used as a reliable and inexpensive alternative to time-consuming procedures such as 3DUS or magnetic resonance imaging. The accurate tumor volume values provided by these formulas may help to provide more reliable estimates of tumor regression or regrowth following globe-preserving treatment of choroidal melanomas, and may be a valuable prognostic indicator.
Tumor size—defined as the largest basal diameter, height, and volume—is a well-established prognostic factor in uveal melanoma. Several mathematical models have been proposed to calculate the tumor volume, with most models based on 2-dimensional ultrasonography to measure the basal diameter and height. However, because these models assume a specific tumor shape, they may prove limited in mushroom and other irregularly shaped tumors. In addition, significant variability among these formulas has been reported. For these reasons, the optimal method of measuring tumor volumes in uveal melanoma remains controversial.
An alternative to mathematical modeling of tumor size is the use of 3-dimensional ultrasound (3DUS). In 3DUS, a rotational transducer is used to take continuous B-scans to create a 3-dimensional block of the tumor. This block can then be sliced and manipulated with the image analyzing software to manually correct surface irregularities, thus increasing the accuracy of the tumor volume measure. The main disadvantage of 3DUS is that it is time-consuming and tedious, thus limiting its clinical use. Recently, however, Romero and associates developed a linear regression formula to overcome this drawback, thus increasing the feasibility of 3DUS. As a result, 3DUS can be considered a viable alternative to mathematical models to determine tumor volumes. However, to the best of our knowledge, these 2 different approaches have never been directly compared to assess their relative accuracy. It is in this context that we conducted the present study.
The main aim of this study was to compare 2 mathematical models to manually corrected 3DUS to determine agreement in estimating tumor volumes in choroidal melanoma. A secondary aim was to assess the effect of the presence or absence of mushroom-shaped tumors on the estimated tumor volumes. We used 2 mathematical formulas, as follows: (1) the formula proposed by Richtig and associates, where volume is calculated for a hemiellipsoidal geometric shape; and (2) a formula developed at our institution, in which the final volume is the sum of 2 geometric volumes: internally a hemiellipsoid, and externally a spheroidal cap.
Methods
Patients and Clinical Assessments
We retrospectively analyzed the tumor measurements of a clinical series of 45 consecutive patients diagnosed with primary choroidal melanoma. All patients underwent 3DUS at their first consultation by a trained specialist in ophthalmic oncology (J.M.C.) in the Ocular Oncology Unit of Bellvitge University Hospital (L’Hospitalet de Llobregat, Barcelona, Spain). Tumor height and the horizontal and vertical basal diameters were measured by A- and B-scan ultrasonography and 3DUS was performed using the OTI-SCAN A-2000 (Ophthalmic Technologies Inc, Toronto, Canada). After obtaining the initial automatic 3DUS block and tumor volume, each of the 36 slices was reassessed by one of the authors (K.M.) and the tumor shape was carefully outlined in each slice to correct for surface irregularities. The time required to contour the entire tumor was approximately 18–20 minutes per patient. Written informed consent was obtained from all subjects in accordance with our institutional guidelines. This study adhered to the tenets of the Declaration of Helsinki. The data of the patients were anonymized for the purposes of this analysis. The confidential information of the patients was protected according to national norms. This manuscript has been revised for its publication by the Clinical Research Ethics Committee of Bellvitge University Hospital.
Mathematical Models
The formula proposed by Richtig and associates (designated Formula 1 in the present study) calculates the tumor as an ellipsoid rotated over the y-axis (height) and divided by 2. Applying this to the volume tumor estimation, the resulting formula would be: 2/3 π.h.a.b; where h is the measured tumor height, a is the measured horizontal basal tumor diameter divided by 2 (to obtain the radius), and b is the measured vertical basal tumor diameter, also divided by 2 ( Figure 1 , Left).
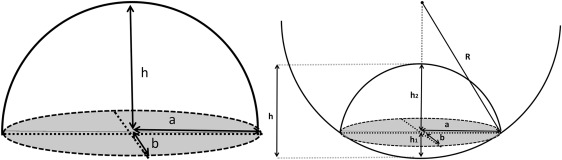
h 1 = R − ( R 2 − a ⋅ b )
; h2=h−h1
h 2 = h − h 1
.
We developed another mathematical model (Formula 2) under the following assumptions: choroidal melanomas typically grow as a hemiellipsoid on the internal surface; however, on the scleral surface, the tumor tends to develop a more spherical shape, as it is limited by the rigidity of the sclera. Thus in our model, we determined the final volume as the sum of 2 geometric shapes: (1) a hemiellipsoid form on the internal side, and (2) a spherical cap, representing the external side of the tumor ( Figure 1 , Right).
Equation 1: Volume of a hemiellipsoid
Equation 2: Volume of a spherical cap
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


