Fig. 16.1
Percentage of correct responses in the melody-discrimination task. Error bars show 95 % confidence intervals
2.3 Discussion
The results suggest that tones above 6 kHz can elicit a salient pitch, sufficient for melody recognition, when they combine to form a harmonic complex tone with a lower F0 (in this case between 1 and 2 kHz). A less interesting interpretation would be that the components are at least partly unresolved and that listeners are sensitivity to the waveform (or temporal envelope) repetition rate of between 1 and 2 kHz, rather than to the individual frequencies. This explanation was unlikely because the tones were presented in random phase, which weakens envelope cues, and because the repetition rates were so high (1–2 kHz) that sensitivity to envelope pitch was expected to be very poor (Carlyon and Deeks 2002). Indeed, two control conditions (run with new groups of six subjects), involving shifted harmonics and dichotic presentation, produced results consistent with predictions based on the processing of individual components, rather than the temporal envelope: when the harmonics were shifted to produce inharmonic complexes but with an unchanged temporal envelope rate, performance dropped to near-chance levels of about 55 %. On the other hand, when the harmonics were presented to opposite ears, performance remained high and not significantly different from that for the original (dichotic) condition. Overall, the results are not consistent with the previously defined “existence region” of pitch (Ritsma 1962). The results also highlight an interesting dissociation, whereby high-frequency tones, which alone do not induce a salient pitch, combine within a complex tone to elicit a salient pitch.
3 Comparing Frequency and F0 Difference Limens
There are different possible explanations for why a dissociation in pitch salience is observed between high-frequency pure tones and complex tones. One possible explanation is that the upper limit for perceiving melodic pitch is determined at a level higher than the auditory nerve, perhaps due to lack of exposure to high (>4 kHz) F0s in normal acoustic environments. Thus, when individual high-frequency tones are presented, they elicit a pitch beyond the “existence region” of melodic pitch. However, when the high-frequency tones are presented in combination with other harmonically related tones, they elicit a pitch corresponding to the F0, which falls within the “existence region.”
Another explanation is that the limits of melodic pitch perception are determined peripherally and that multiple components elicit a more salient pitch simply due to a combination of multiple independent information sources. Based on the results from lower frequencies, this explanation seems less likely: little or no improvement in pitch discrimination is found when comparing the results from individual pure tones with the results from a complex tone comprised of those same pure tones (Faulkner 1985; Goldstein 1973). However, similar measurements have not been made at high frequencies, so it is unclear whether a similar pattern of results would be observed.
3.1 Methods
Seven young normal-hearing listeners participated in this experiment, screened as before for detection thresholds in quiet at 16 kHz no higher than 50 dB SPL. Difference limens for complex-tone F0 (F0DLs) and difference limens for pure-tone frequency (FDLs) were measured. Two nominal F0s were tested: 280 Hz and 1,400 Hz. FDLs were measured for two sets of eight nominal frequencies, corresponding to harmonics 5–12. The complex tones were generated by band-pass-filtering broadband harmonic complexes, such that only harmonics 5–11 of the complex tones at the nominal F0s were within the filter passband. All tones were presented at a level of 55 dB SPL per component within the filter passband. The filter slopes were 30 dB/octave. As in the previous experiment, random component starting phases were used on each presentation. The tones were 300-ms long each, including 10-ms onset and offset ramps, and both pure and complex tones were presented in the same combination of broadband noise and low-pass TEN that was used in the previous experiment. The background noise started 200 ms before the onset of the first tone and ended 200 ms after the offset of the last tone, for the current trial. The interstimulus interval was 500 ms.
The F0DLs and FDLs were measured using both a 2I-2AFC task and a 3I-3AFC task. The first requires a labeling (up vs. down), whereas the second requires only identification of the interval that was different. For both tasks, thresholds were measured using an adaptive, two-down one-up procedure (Levitt 1971). The stimuli were generated digitally and played out via a soundcard (Lynx Studio L22) with 24-bit resolution and a sampling frequency of 48 kHz. They were presented monaurally to the listener via Sennheiser HD 580 headphones.
3.2 Data Analysis
The individual FDLs within each of the two spectral regions were used to compute predicted F0DLs for the respective spectral region using the following equation:
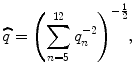
where 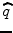 is the predicted F0DL and θ n denotes the FDL measured using a nominal test frequency corresponding to the n th harmonic of the considered nominal F0. The equation stems from the general equation for predicting sensitivity based on multiple, statistically independent observations, assuming an optimal (maximum-likelihood ratio) observer (Goldstein 1973; Green and Swets 1966). The measured and predicted thresholds were log-transformed before statistical analyses using repeated measure analyses of variance (ANOVAs).
is the predicted F0DL and θ n denotes the FDL measured using a nominal test frequency corresponding to the n th harmonic of the considered nominal F0. The equation stems from the general equation for predicting sensitivity based on multiple, statistically independent observations, assuming an optimal (maximum-likelihood ratio) observer (Goldstein 1973; Green and Swets 1966). The measured and predicted thresholds were log-transformed before statistical analyses using repeated measure analyses of variance (ANOVAs).
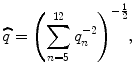
(16.1)
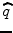 is the predicted F0DL and θ n denotes the FDL measured using a nominal test frequency corresponding to the n th harmonic of the considered nominal F0. The equation stems from the general equation for predicting sensitivity based on multiple, statistically independent observations, assuming an optimal (maximum-likelihood ratio) observer (Goldstein 1973; Green and Swets 1966). The measured and predicted thresholds were log-transformed before statistical analyses using repeated measure analyses of variance (ANOVAs).
is the predicted F0DL and θ n denotes the FDL measured using a nominal test frequency corresponding to the n th harmonic of the considered nominal F0. The equation stems from the general equation for predicting sensitivity based on multiple, statistically independent observations, assuming an optimal (maximum-likelihood ratio) observer (Goldstein 1973; Green and Swets 1966). The measured and predicted thresholds were log-transformed before statistical analyses using repeated measure analyses of variance (ANOVAs).3.3 Results
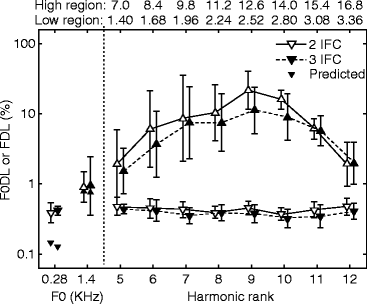
Figure 16.2 shows the mean F0DLs and FDLs for the two F0s and two tasks (2- or 3-AFC). Considering first the complex-tone F0DLs, a two-way RMANOVA was performed on the log-transformed data, with the task (2I-2AFC, 3I-3AFC) and F0 (280 Hz, 1,400 Hz) as within-subject factors. No significant main effect of task was observed [F(1, 6) = 0.08, p = 0.786]. The effect of nominal F0 just failed to reach significance [F(1, 6) = 5.57, p = 0.056]. No significant interaction between the two factors was observed either [F(1, 6) = 0.015, p = 0.906].