Objective
To investigate the distribution of ocular torsion in patients with intermittent exotropia and to determine possible correlation between the torsion and the severity of intermittent exotropia.
Design
Prospective, comparative study comprising 600 eyes of 300 children.
Methods
One hundred fifty patients with intermittent exotropia between 4 and 15 years of age and another 150 age-matched normal controls without strabismus were enrolled prospectively. Digital nonmydriatic fundus photographs were obtained from both eyes of each subject and the disc–foveal angle was calculated using digital image software. All photographs also were graded as normal, extorsion, or intorsion. We compared the size of the disc–foveal angle between the normal and intermittent exotropia group. We analyzed possible correlations between the disc–foveal angle and disease severity factors, including amount of exotropia, Titmus stereoacuity, and duration of strabismus.
Results
Mean disc–foveal angle of intermittent exotropia group was significantly larger than that of normal control group (6.13 and 5.13 degrees, respectively; P < .01). Ocular torsion (either extorsion or intorsion) was discovered in 45 (30%) patients among the intermittent exotropia group, whereas it was found in only 16 (11%) individuals among the normal control group ( P < .01). The size of disc–foveal angle showed significant positive correlations with the amount of exotropia and the degree of stereoacuity ( r = 0.45, P < .01, and r = 0.51, P < .01, respectively).
Conclusions
Ocular torsion could be found not infrequently in patients with intermittent exotropia. Furthermore, the amount of torsion showed a significant relationship to the disease severity of intermittent exotropia. Assessment of ocular torsion could be used as a supplementary tool for evaluating fusion in patients with intermittent exotropia.
Ocular torsion refers to the anatomic cycloposition of an eye around its visual axis and has been acknowledged widely as an integral component of eye movement in humans. Together with the horizontal and vertical ocular alignment, the torsional alignment also makes a substantial contribution to the precise control of the binocular motor correspondence. This 3-dimensional ocular motor control minimizes the disparity of images.
The ocular torsion can be measured objectively or subjectively. Although subjective torsion depends on the patient’s sensory adaptation to the cyclodeviation, objective torsion demonstrates only how far the eye is rotated anatomically away from the normal position itself. A recent study showed that objective torsion was the same regardless of which eye was used for fixation. This result supports the idea that assessment of objective ocular torsion may function as a valid and reliable way to evaluate cyclovertical muscular tonus in the examined eye, while being unaffected by fixational or fusional cyclovergence stimuli. There have been numerous studies attempting to measure the amount of objective ocular torsion. Since von Graefe reported the use of ophthalmoscopy in observing vertical macular displacement in a patient with incyclotropia, direct observation of fundus has been a mainstay of ocular torsion evaluation. More recently, although some other alternative techniques, including slit-lamp biomicroscopy, iris photography, and automated perimetry, have been proposed, fundus photography has emerged as the most commonly used method for assessing objective ocular torsion. Because of its simplicity, low cost, and easy applicability, fundus photography is regarded as a current standard for measuring ocular torsion.
Prior studies using fundus photography revealed that there was some degree of ocular torsion even in normal individuals. In addition, a number of studies also have been conducted on ocular torsion in patients with strabismus. Most of those studies, however, have focused mainly on cyclovertical strabismus, such as congenital or acquired superior oblique palsy, A-pattern or V-pattern strabismus, or dissociated vertical deviation. In contrast, to date, there have been no studies of ocular torsion among patients with intermittent exotropia.
Intermittent exotropia is one of the most prevalent strabismic disorders, yet it remains far from fully explored, especially regarding its pathogenesis and treatment. Intermittent exotropia is unique in that it is controlled intermittently by fusional mechanisms, and later may progress to constant exotropia with loss of control. Because this type of exotropia is a horizontal form of strabismus, it is seemingly regarded as not related to the cyclotorsion. However, in our clinical experience, we observed fundus torsion in a large number of patients with typical intermittent exotropia. It seems reasonable to assume that the ocular torsion in intermittent exotropia may be an obstacle for the patients obtaining or maintaining their binocular fusion. With these in mind, we aimed to investigate the distribution of objective ocular torsion among patients with intermittent exotropia and to determine whether the amount of ocular torsion correlates with the clinical severity of intermittent exotropia.
Methods
In this comparative observational study, we prospectively enrolled 150 consecutive patients between the ages of 4 and 15 years who were diagnosed with basic intermittent exotropia from a single tertiary eye care center (Asan Medical Center). The patients sought treatment from our pediatric eye clinic between March and August of 2011.
The diagnosis of basic intermittent exotropia was made when the distance deviation was within 10 prism diopters of that at near. Patients were excluded if there was any neurologic deficit, developmental delay, systemic genetic disorders, alphabet pattern strabismus (A, V, Y, X, or λ), overelevation or depression in adduction, coexisting vertical deviation, other significant ocular diseases (superior oblique palsy, congenital cataract, retinopathy of prematurity, or other congenital ocular anomalies), previous history of strabismus surgery, or unilateral amblyopia of any degree affecting fixation behavior.
For comparison, we also recruited 150 age-matched, healthy subjects without any significant ocular disease, heterotropias, or even heterophorias as controls. This control subjects were derived from the pediatric vision care clinic in our institution and were excluded if they had significant amblyogenic refractive errors (myopia ≤ −3.0 diopters [D], hyperopia ≥ +3.0 D, astigmatism ≥ 1.5 D, anisometropia ≥ 1.5 D) or any degrees of ocular misalignment on the alternating cover test.
All enrolled subjects underwent a full ophthalmic examination including extraocular motility testing, Titmus stereo testing (Titmus Optical Co, Petersburg, Virginia, USA), and digital fundus photography. We recorded the following clinical data for all subjects: age, gender, duration of strabismus if any, visual acuity, refraction, distance angle of exotropia in primary position, and Titmus stereoacuity. In addition, for the intermittent exotropia patients, we determined the preferred eye for fixation by cover and uncover test. When it was difficult to determine which eye was the preferred eye by this test, we used a hole-in-the-card test in combination with a near-point convergence test.
We measured ocular torsion for both eyes of every subject using a digital nonmydriatic fundus photography. Fundus photographs were obtained by a TRC-50DX (Topcon Medical System, Tokyo, Japan) with the patients being asked to look at the internal fixation target to align the patients’ eyes to be at the primary position. To prevent inadvertent head tilting, photographers were asked to ensure the horizontal position of the patients’ eyes by using the side marks as a guide. The disc–foveal angle was calculated from a well-focused and well-centered single photograph using Pentavision image software (Asan Medical Center, Seoul, Korea) and a built-in protractor. The detailed method of disc–foveal angle calculation was described previously. Two lines were drawn: one straight horizontal line passing through the geometric center of the optic disc and the other line joining the center of the disc and the fovea. The angle between these 2 lines was calculated digitally to obtain the disc–foveal angle. Three separate measurements were made for each eye and their averages were recorded. All the measurements were performed by the first author (K.H.S.) who was masked to the clinical diagnosis.
In addition to this quantitative measurement of the ocular torsion, we also evaluated all of the photographs qualitatively and categorized them into normal, intorsion, or extorsion categories according to the following clinical criteria commonly used in our strabismus practice. Eyes were categorized as having intorsion when the fovea was located above the geometric center of the optic disc, as having extorsion when the fovea was located below the inferior margin of the optic disc, and as normal when the location of the fovea was in an area between the center of the disc and the inferior margin of the disc ( Figure 1 ).
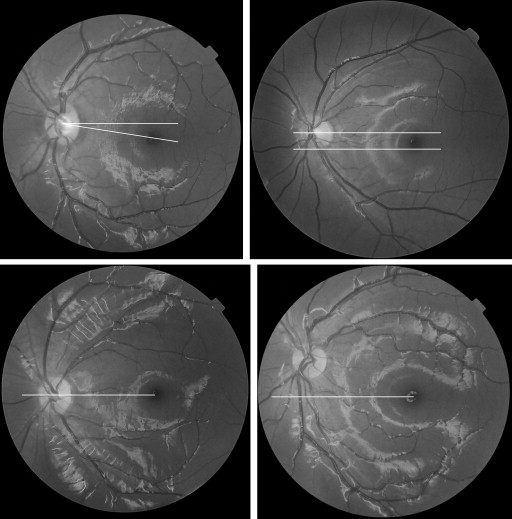
We compared both the quantitative and qualitative torsion between the intermittent exotropia group and normal control (no strabismus) groups. In addition, we analyzed correlations between the amount of torsion and the clinical severity of strabismus in the intermittent exotropia group. As for the clinical severity, we used the following variables: distance angle of exotropia, Titmus stereoacuity, and duration of strabismus. All statistical analyses were conducted using SPSS software for Windows version 13.0 (SPSS Inc, Chicago, Illinois, USA), and P < .05 was considered to indicate significance.
Results
A total of 300 subjects (600 eyes) were assessed in the present study. One hundred fifty patients (300 eyes) who met eligibility criteria were included in the intermittent exotropia group. Another 150 age-matched healthy individuals (300 eyes) without any ocular misalignment were participated as a control group. There was no statistically significant difference between the 2 groups with regard to age, sex ratio, or refraction ( Table ).
| Intermittent Exotropia | Normal Controls | P Value | |
|---|---|---|---|
| Mean age ± SD (y) | 6.96 ± 4.21 | 7.03 ± 1.93 | .54 a |
| Male gender | 74 (49.3%) | 71 (47.3%) | .73 b |
| MRSE ± SD (diopters) | −1.70 ± 1.40 | −1.49 ± 2.40 | .36 a |
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


