Modeling Effects of Precursor Duration on Behavioral Estimates of Cochlear Gain

(7.1)

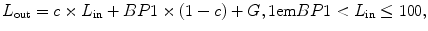
${L}_{\text{out}}=c\times {L}_{\text{in}}+BP1\times (1-c)+G,\text{{1em}}BP1<{L}_{\text{in}}\le 100,$

(7.2)

where L _in is input signal level, L _out is masker level, G is gain, BP1 is breakpoint, and c is the slope between BP1 and 100 dB. The modification by Jennings and Strickland (2010) included parameter α to represent constant low-level internal noise. The intensity of α is subtracted from the intensity levels of L _in and BP1 in Eqs. 7.1 and 7.2. The parameter estimates of the fits are presented in Fig. 7.1.

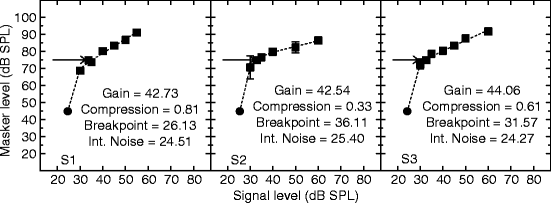
Fig. 7.1

GOM data (filled squares) with I/O function fits (dashed lines). Filled circles are quiet threshold. Arrows indicate fixed masker levels for Exp. II

5 Results: Experiment II

On-frequency precursor data are shown as filled symbols in Fig. 7.2. Open symbols are off-frequency precursor data. The dashed horizontal line is threshold for the control condition. The difference between each threshold and this line is assumed to reflect the amount of gain reduction by the precursor. In some panels, on-frequency precursor thresholds increase with increasing precursor duration up to 50 ms and then roll over, forming an oscillating pattern. In other panels, thresholds increase with duration up to about 50 ms then plateau for longer durations. Off-frequency precursor thresholds generally increased with increasing duration. A repeated-measures mixed model ANOVA was performed to evaluate the effects of precursor frequency, level, and duration on threshold. We also evaluated the effect of subject. All main effects were significant (p < 0.01). All two-way interactions were also significant (p < 0.01), including a significant interaction of frequency × duration, F(6,396) = 27.19 (p < 0.0001), which supports our hypothesis that the effect of duration differs for the two precursor frequencies. A three-way interaction of subject × frequency × duration was not significant.

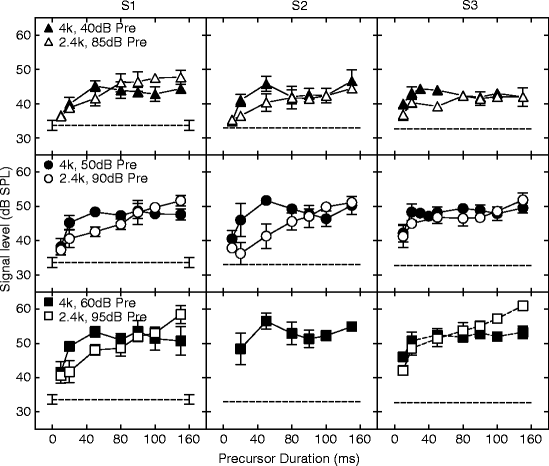
Fig. 7.2

Precursor duration data for on-frequency (filled symbols) and off-frequency (open symbols) precursors. Dashed lines are thresholds with a 0.8-kHz precursor

6 Modeling

We used MATLAB (MathWorks, Natick, MA) to model our results. We compared the standard TWM to a modified TWM with history-dependent gain variation simulating the MOCR. The TWM in its standard form includes four main modules (Oxenham and Moore 1994). The first is peripheral filtering. Second is a compressive nonlinearity representing the basilar membrane I/O function, followed by half-wave rectification. Third is a sliding integrating window. The window for forward masking is

$W(t)=(1-w)exp(t/{T}_{1})+w exp(t/{T}_{2})$

(7.3)

where W describes window shape, t is time relative to the window center, T ₁ and T ₂ are time constants, and w is the weighting of the relative contribution of T ₁ and T ₂. The fourth module is a decision mechanism where the maximum ratio of masker + signal to masker-alone (SNR) is determined. It is assumed that this SNR is constant across conditions.

In our version of the TWM, instead of a filtering module, stimuli were classified as on- or off-frequency relative to the signal and were represented as half-wave rectified envelopes. Output levels were determined on a point-by-point basis with a sampling rate of 10 kHz. Off-frequency stimuli had a linear representation at the signal frequency; only the intercept β was free to vary (Output = Input – β). On-frequency stimuli were subjected to compressive nonlinearity (Eqs. 7.1 and 7.2 with no internal noise). G, c, and BP1 remained fixed at the original parameter estimates (Fig. 7.1). Internal noise limited the output minimum of all stimuli. The on- and off-frequency outputs were combined and convolved with the forward masking window (Eq. 7.3). This procedure was repeated for each condition over a range of signal levels. Threshold predictions were determined by minimizing RMS error on β, T ₁, T ₂, w, and SNR. For each subject, all data were fit at once. Parameter estimates and RMS errors are presented in Table 7.1

Table 7.1

Parameter estimates and RMS errors for TWM and TWM-GR fits